итог

1. Экономические задачи, решаемые методами динамического программирования

2. Задача распределения ресурсов

3. Задача распределения ресурсов

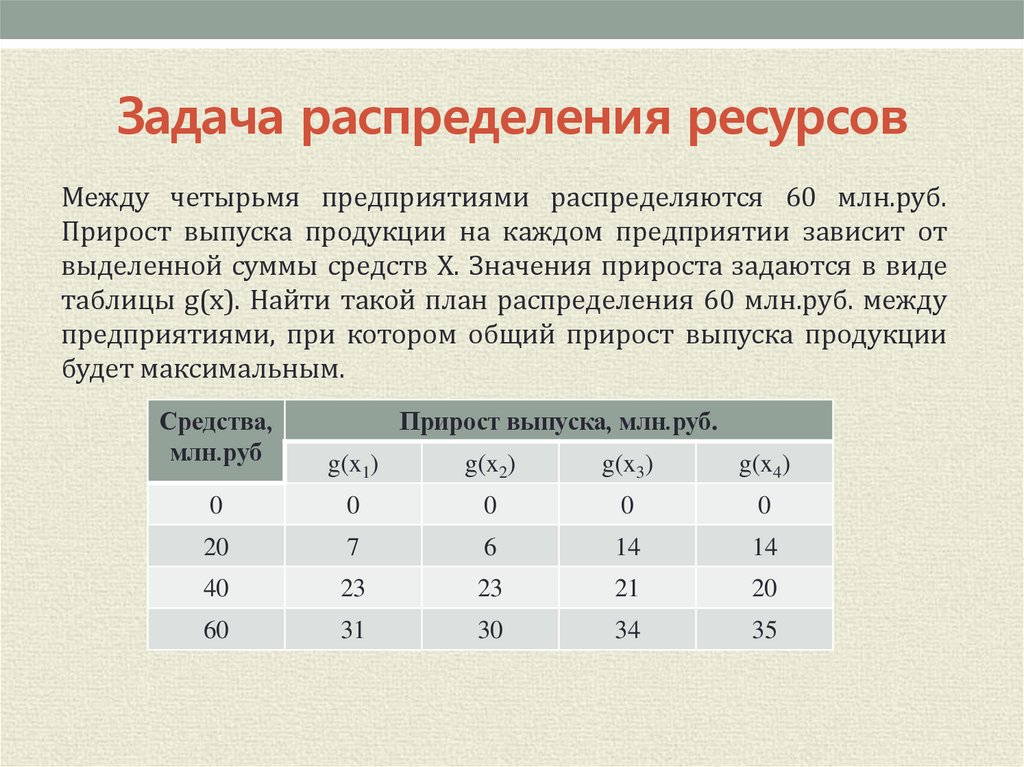
Между четырьмя предприятиями распределяются 60 млн.руб.
Прирост выпуска продукции на каждом предприятии зависит от
выделенной суммы средств X. Значения прироста задаются в виде
таблицы g(x). Найти такой план распределения 60 млн.руб. между
предприятиями, при котором общий прирост выпуска продукции
будет максимальным.
Средства,
млн.руб
Прирост выпуска, млн.руб.
g(x1)
g(x2)
g(x3)
g(x4)
0
0
0
0
0
20
7
6
14
14
40
23
23
21
20
60
31
30
34
35

4. Общая постановка задачи инвестирования

A1
A2
…
An
x1
f1(x1)
f2(x1)
…
fn(x1)
x2
f1(x2)
f2(x2)
…
fn(x2)
…
…
…
…
…
xm
f1(xm)
f2(xm)
…
fn(xm)
Требуется найти такой план распределения между предприятиями
денежной суммы
максимальной.
,
при
котором
суммарная
прибыль
будет

5.

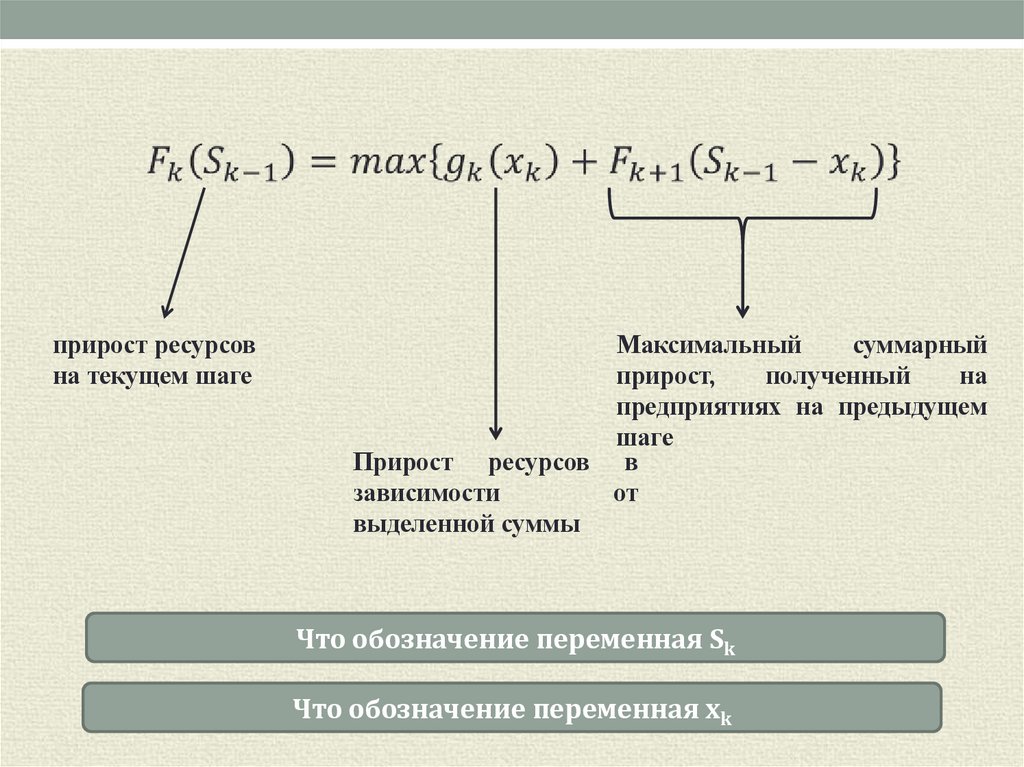
прирост ресурсов
на текущем шаге
Максимальный
суммарный
прирост,
полученный
на
предприятиях на предыдущем
шаге
Прирост ресурсов в
зависимости
от
выделенной суммы
Что обозначение переменная Sk
Что обозначение переменная xk

6.

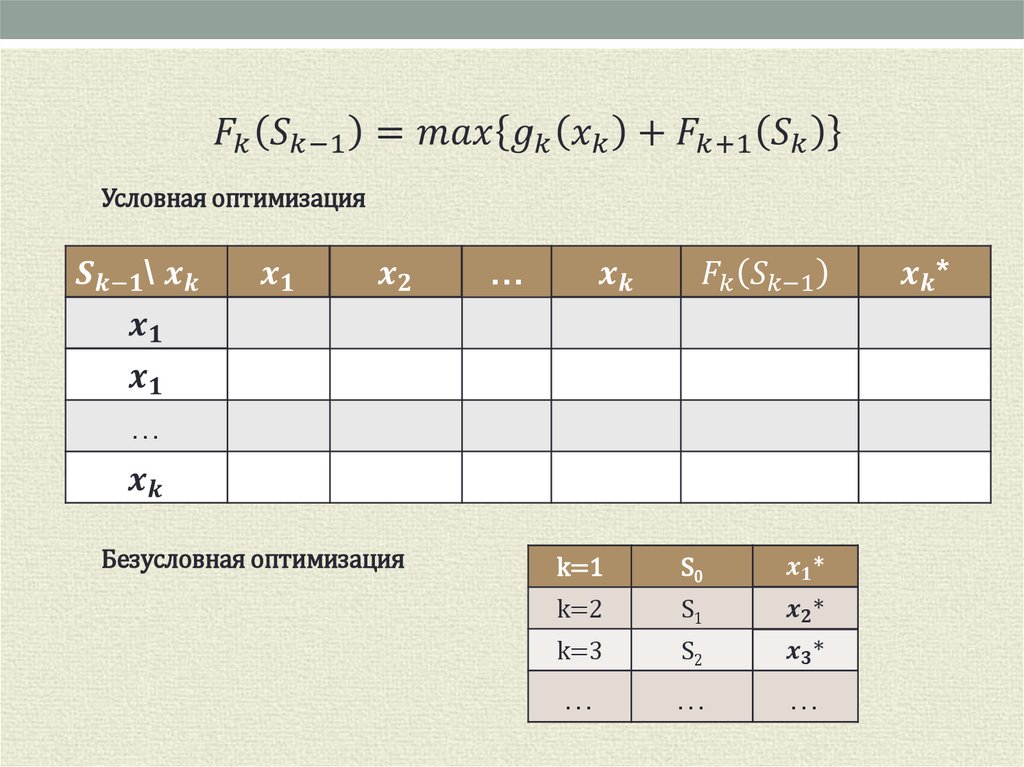
Условная оптимизация
…
…
Безусловная оптимизация
k=1
S0
k=2
S1
k=3
S2
…
…
…

7. Задача

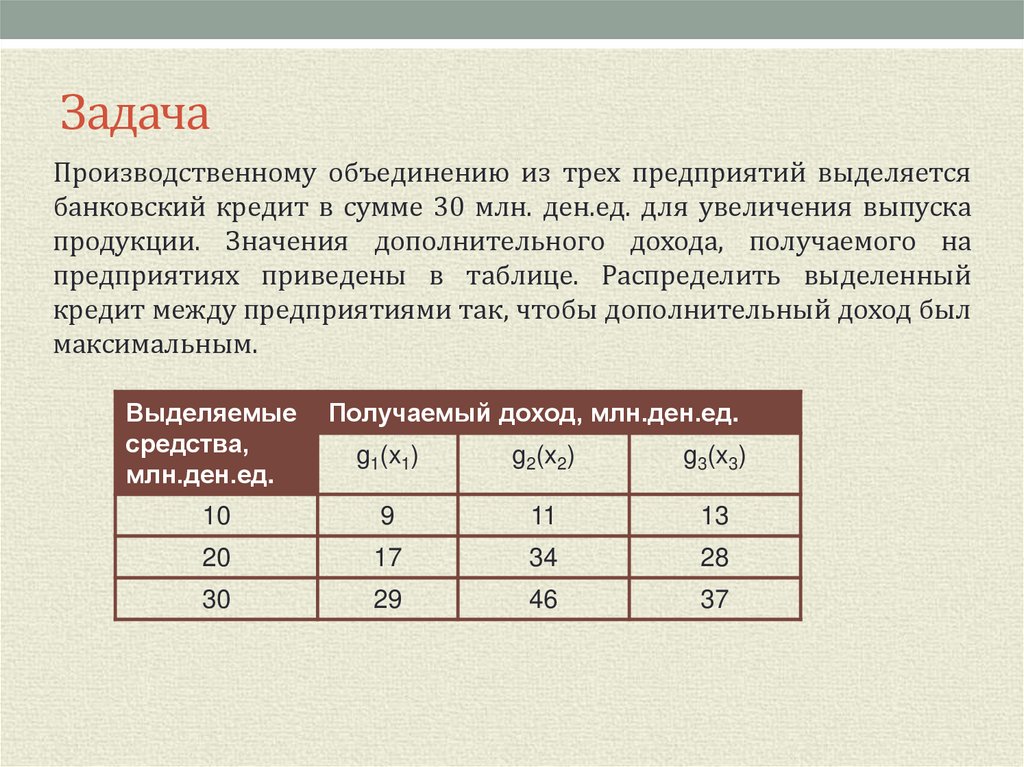
Производственному объединению из трех предприятий выделяется
банковский кредит в сумме 30 млн. ден.ед. для увеличения выпуска
продукции. Значения дополнительного дохода, получаемого на
предприятиях приведены в таблице. Распределить выделенный
кредит между предприятиями так, чтобы дополнительный доход был
максимальным.
Выделяемые
средства,
млн.ден.ед.
Получаемый доход, млн.ден.ед.
g1(x1)
g2(x2)
g3(x3)
10
9
11
13
20
17
34
28
30
29
46
37

8.  

S2\x3
0
0
0
10
10
20
30
F3(S2)
x3*
0
13
0
10
28
20
37
30
13
28
20
37
30
F2(S1)
x2*
0 +0=0
0
0
13
0
20
0 +13=13 11 +0=11
0 +28=28 11 +13=24 34 +0=34
34
20
30
0+37=37
47
20
S2\x3
0
0
10
10
20
11 +28=39 34 +13=47
30
46+0=46

9.  

S0\x1
0
10
20
0
0 +0=0
10
0+13=13
9 +0=9
20
0 +34=34
9 +13=22
17 +0=17
30
0 +47=47
9 +34=43
17 +13=30
Дополнительный доход будет составлять
при k=1 S0=30
30
29 +0=29
47
F1(S0)
x1*
0
0
13
0
34
0
47
0
ден.ед
x1* 0 тогда S1=S0-x1* =30-0=30
при k=2 S1=30 x2* 20 тогда S2=S1-x2* =30-20=10
при k=3 S2=10 x3* 10

10. Ответ:

Найденное оптимальное распределение кредита можно
записать в виде вектора x* 0;20;10
Максимальный прирост продукции составит
47 млн.ден.ед.

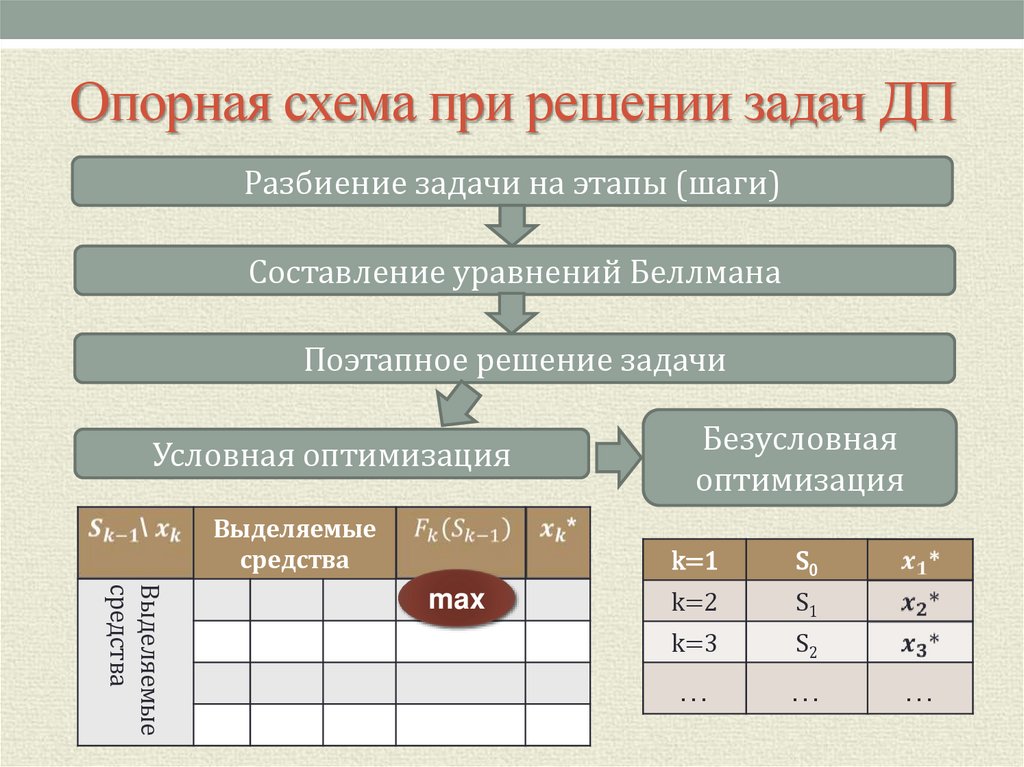
11. Опорная схема при решении задач ДП

Разбиение задачи на этапы (шаги)
Составление уравнений Беллмана
Поэтапное решение задачи
Условная оптимизация
Выделяемые
средства
Выделяемые
средства
max
Безусловная
оптимизация
k=1
S0
k=2
S1
k=3
S2
…
…
…

12. Задача распределения ресурсов

13. Задача распределения ресурсов

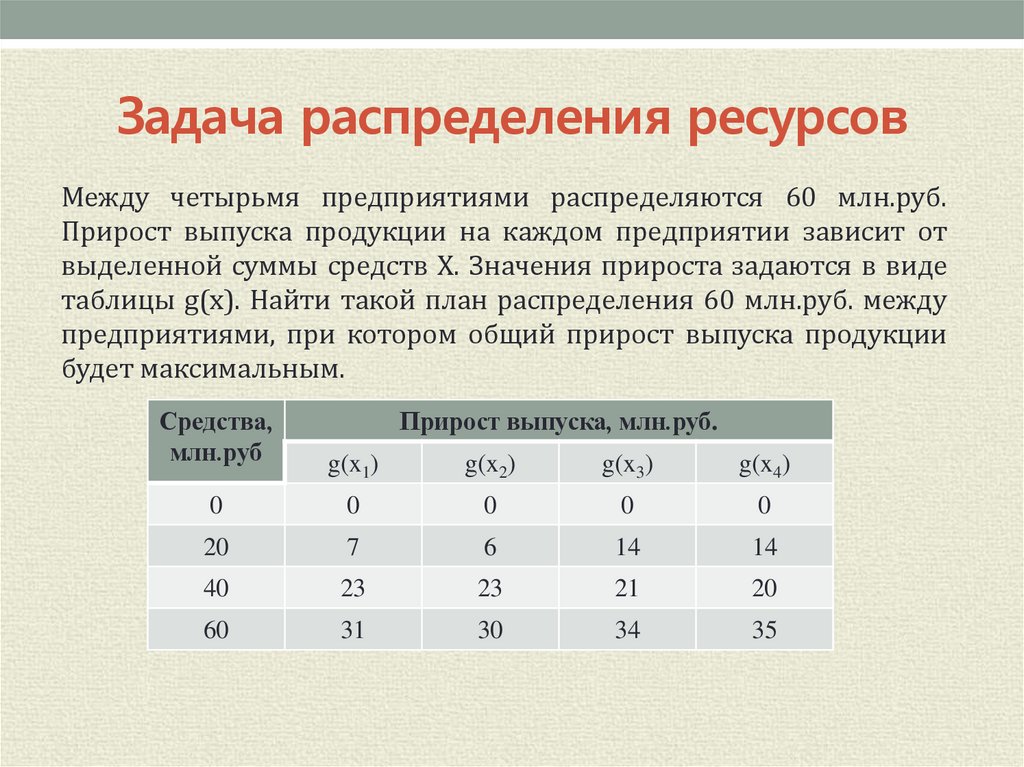
Между четырьмя предприятиями распределяются 60 млн.руб.
Прирост выпуска продукции на каждом предприятии зависит от
выделенной суммы средств X. Значения прироста задаются в виде
таблицы g(x). Найти такой план распределения 60 млн.руб. между
предприятиями, при котором общий прирост выпуска продукции
будет максимальным.
Средства,
млн.руб
Прирост выпуска, млн.руб.
g(x1)
g(x2)
g(x3)
g(x4)
0
0
0
0
0
20
7
6
14
14
40
23
23
21
20
60
31
30
34
35

14.

S3\x4
0
0
0
20
20
40
60
14
40
20
60
35
S3\x2
0
20
40
0
0
20
14
14
40
20
28
21
60
35
34
35
F4(S3)
x4*
0
0
14
20
20
40
35
60
60
34
F3(S2)
x3*
0
0
14
0 или 20
28
20
35
0 или 40

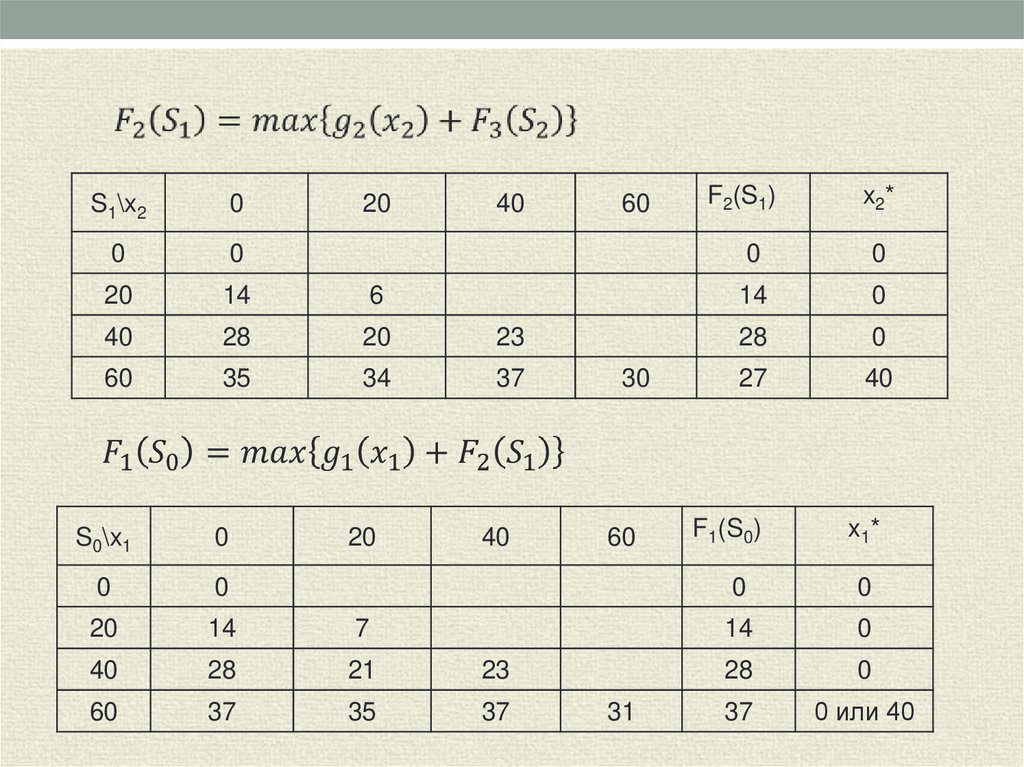
15.

S1\x2
0
20
40
0
0
20
14
6
40
28
20
23
60
35
34
37
S0\x1
0
20
40
0
0
20
14
7
40
28
21
23
60
37
35
37
F2(S1)
x2*
0
0
14
0
28
0
30
27
40
60
F1(S0)
x1*
0
0
14
0
28
0
37
0 или 40
60
31

16. Ответ:

Дополнительный доход будет составлять
1
2
k=1
S0=60
x1*=0
k=2
S1=60
x2*=40
k=3
S2=20
k=4
37
ден.ед
k=1
S0=60
x1*=40
k=2
S1=20
x2*=0
x3*=0
k=3
S2=20
x3*=0
S3=20
x4*=20
k=4
S3=20
x4*=20
k=1
S0=60
x1*=0
k=1
S0=60
x1*=40
k=2
S1=60
x2*=40
k=2
S1=20
x2*=0
k=3
S2=20
x3*=20
k=3
S2=20
x3*=20
k=4
S3=0
x4*=0
k=4
S3=0
x4*=0
3
4

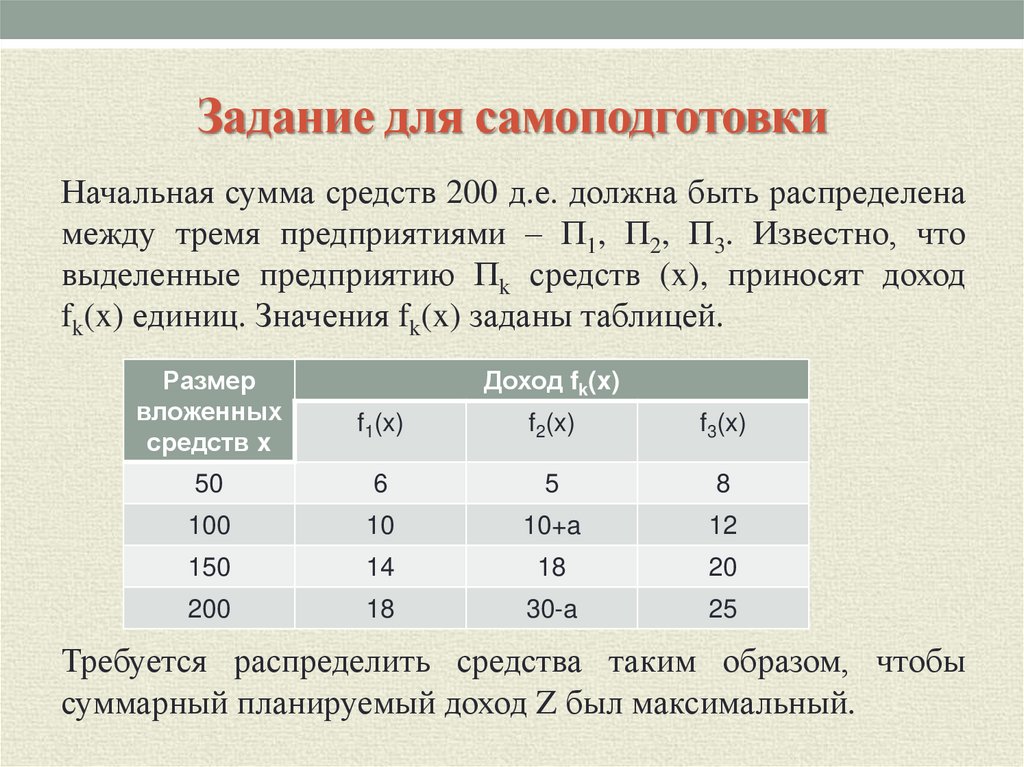
17. Задание для самоподготовки

Начальная сумма средств 200 д.е. должна быть распределена
между тремя предприятиями – П1, П2, П3. Известно, что
выделенные предприятию Пk средств (x), приносят доход
fk(x) единиц. Значения fk(x) заданы таблицей.
Размер
вложенных
средств x
Доход fk(x)
f1(x)
f2(x)
f3(x)
50
6
5
8
100
10
10+a
12
150
14
18
20
200
18
30-a
25
Требуется распределить средства таким образом, чтобы
суммарный планируемый доход Z был максимальный.