Динамическое программирование. (Семинар 3)

1. Динамическое программирование

Семинар 3:
Динамическое программирование

2. Задача динамического программирования

Рассмотрим
динамическую систему,
которая последовательно за n шагов
переходит из состояния s 0 в состояние s n
Промежуточные состояния s i определяют
состояния системы после i-го шага. Как
правило, состояния системы определяются
несколькими числами,
r поэтому
предполагается, что s i являются
ur
векторами, т.е. s = ( s1 , s 2 ,..., s m )
i
i
i
i
2

3.

uur
Переход системы
из состояния si -1 в
r
состояние s i определяется
параметрами
ur
(управлениями) ui (i = 1,..., n) при
помощи
v уравнения
v v состояний
s i = Fi ( s i-1 , u i )
Эффективностьr каждого
шага оценивается
r
функциями f i ( s i-1 , u i ) .
Таким
образом, эффективность всего
процесса характеризуется суммой
r r
r r
r r
z1 = f1 (s 0 , u 1 ) + f 2 (s 1 , u 2 ) + ... + f n (s n-1 , u n )
3

4.

Задача
состоит
r вr том,r чтобы найти набор
управлений u , u ,..., u , оптимизирующий z1
(далее предполагается, что решается задача
на максимум): r
1
*
1
2
n
*
1
z = z ( s 0 ) = max
uur uur z1
u1 ,u2 ,...,un
Процесс
решения разбивается на n шагов.
Введём функцию:
( ) (
)
(
)
(
)
zi s i-1 = fi s i-1 , u i + fi+1 s i , u i+1 + ... + f n s n-1 , u n , i = 1,2...., n
- эта функция характеризует
rэффективность
r
перехода от состояния s i к s n .
4

5.

Последовательно
оптимизируем
r
r
r
r
*
*
*
*
zn s n-1 , zn-1 s n-2 ,..., z2 s 1 , z1 s 0
( )
( )
( ) ( )
По
формулам, называемым уравнениями
Беллмана
*
z n ( s n -1 ) = max f n s n -1 , u n
un
(
)
5

6.

z
*
n -1
zn*-2
r
s n-2 = max f n-1
un-1
r
s n-3 = max f n-2
( )
( )
un - 2
( (
( (
r r
r
r
r r
*
s n-2 , u n-1 + zn sгде
s,
Fn-1 = s n-1 u n-2 , n-1
n-1
r r
r
r
r r
*
s n-3 , u n-2 + zn-1 sгде
s,
Fn-2 = s n-2u n-3 , n-2
n-2
) ( ))
) ( ))
(
)
(
)
L L L L L L L L L L L L L L L L L L L L L
r r
r
r
r r
*
*
z2 s1 = max f 2 s 1 , u 2 + z3 sгде
,s F2 =s 2u 1 , 2
2
u2
r
r r
r
r
r r
*
*
z1 ( s 0 ) = max f1 s 0 , u n-1 + z2 sгде
, s F1 =s 1 u 0 , 1
1
( )
u1
( (
( (
) ( ))
) ( ))
(
(
)
)
находим максимальное решение задачи.
6

7. Задача о распределении средств между предприятиями

Процесс
решения задачи начинается с
оптимизации последнего шага, что
называется обратным ходом вычислений и
свойственно
многим
задачам
динамического программирования.
Рассмотрим теперь несколько задач о
распределении
средств
между
предприятиями на несколько лет.
7

8.

Задача 1
Планируется
работа
двух
отраслей
промышленности на n лет. Начальные
ресурсы составляют S0 у.е. Средства x,
вложенные в первую отрасль в начале года,
дают в конце года прибыль f1 ( x ) = 0,3x и
возвращаются в размере j1 ( x ) = 0,1
.x
Аналогично, для второй отрасли прибыль
составляет f 2 ( y ) = 0,2 y , а возврат j2 ( y ) = 0,3 y
8

9.

Задача 1
В
конце каждого года возвращённые
средства
полностью
распределяются
между
предприятиями.
Определить
оптимальный план распределения средств
и найти максимальную прибыль, если
n = 4, а s0 = 10000
9

10.

Решение:
Динамической системой являются два
si
предприятия, состояния которых
r
определяются
вложенными
в 2 них
1
средствами, а управления u i = ui , ui на
k
ui
i-м году являются средствами ,
переданные k-й отраслью.
• Так
как
возвращённые
средства
распределяются полностью,
то имеет
1
2
место условие si -1 = ui + ui
2
1
• т.е. ui = si -1 - ui
и фактически задача
одномерна.
(
)

11.

Далее
будем считать, что управление на i1
м году определяется числами ui = ui , т.е.
средствами, выделенными первой отрасли.
В силу того же условия уравнения
состояний имеют вид:
si = F ( si -1 , ui ) = j1 (ui ) + j 2 ( si -1 - ui ) = 0,1ui + 0,3( si -1 - ui )
= 0,3si -1 - 0,2ui
А
прибыль на i-м году равна:
f ( si -1 , ui ) = f1 (ui ) + f 2 ( si -1 - ui ) = 0,3ui + 0,2( si -1 - ui )
= 0,2 si -1 + 0,1ui
11

12.

Решение
задачи начинается с оптимизации
функции z 3 ( s3 ) :
z 3 ( s3 ) = max f ( s3 , u4 ) = max f1 (u4 ) + f 2 ( s3 - u4 ) =
*
0 u 4 s3
max 0,2 s3 + 0,1u4
0 u 4 s3
0 u 4 s3
Для
вычисления максимума заметим, что
требуется найти максимум линейной
функции на отрезке, поэтому:
*
*
z ( s3 ) = max 0,2s3 + 0,1u4 = 0,3s3 при u 4 = s3
0 u s
3
4
3
si = 0,3si -1 - 0,2ui
f ( si -1 , ui ) = 0,2 si -1 + 0,1ui
12

13.

Далее,
z 2* ( s2 ) = max f ( s2 , u3 ) + z3* ( s3 ) = max 0,2 s2 + 0,1u3 + 0,3s3 =
0 u3 s 2
0 u3 s 2
= max 0,2s2 + 0,1u3 + 0,3(0,3s2 - 0,2u3 ) =
0 u3 s 2
*
u
при 3 = s2
= max 0,29 s2 + 0,04u3 = 0,33s2
0 u3 s 2
z1* ( s1 ) = max f ( s1 , u2 ) + z 2* ( s2 ) = max 0,2s1 + 0,1u2 + 0,33s2 =
0 u 2 s1
0 u 2 s1
= max 0,2s1 + 0,1u2 + 0,33(0,3s1 - 0,2u2 ) =
0 u 2 s1
= max 0,299 s1 + 0,034u2 = 0,333s1
0 u 2 s1
si = 0,3si -1 - 0,2ui
при u2* = s1
f ( si -1 , ui ) = 0,2 si -1 + 0,1ui

14.

z0* ( s0 ) = max f ( s0 , u1 ) + z1* ( s1 ) = max 0,2 s0 + 0,1u1 + 0,333s1 =
0 u1 s0
0 u1 s0
= max 0,2 s0 + 0,1u1 + 0,333(0,3s0 - 0,2u1 ) =
0 u1 s0
= max 0,2999 s0 + 0,0334u1 = 0,3333s0
0 u1 s0
*
u
при 1 = s0
Таким образом, поскольку на каждом шаге
ui* = si -1
,то средства каждый год вкладываются
в первую
s1 = j1 ( s0 )отрасль:
= 0,1s0 = 1000
у.е.
s2 = j1 ( s1 ) = 0,1s1 = 100
у.е.
s3 = j1 ( s2 ) = 0,1s2 = 10
у.е.
si = 0,3si -1 - 0,2ui
f ( si -1 , ui ) = 0,2 si -1 + 0,1ui

15.

Максимальная
прибыль равна
*
z0 ( s0 ) = 0,3333s0 = 3333 у.е.
Полученные результаты можно записать в
виде таблицы, в которой по годам указано
распределение средств:
1 год
2 год
3 год
4 год
I
10 000
1 000
100
10
II
0
0
0
0

16.

Задача 2
Планируется
работа
двух
отраслей
промышленности на n лет. Начальные
ресурсы составляют S0 у.е. Средства x,
вложенные в первую отрасль в начале года,
дают в конце года прибыль f ( x ) = 0,9 x и
1
возвращаются в размере
.
j
x
=
0,7
x
(
)
1
Аналогично, для второй отрасли прибыль
составляет
, а возврат
f 2 ( y ) = 0,8 y
j2 ( y ) = 0,9 y
16

17.

Задача 2
В
конце каждого года возвращённые
средства
полностью
распределяются
между
предприятиями.
Определить
оптимальный план распределения средств
и найти максимальную прибыль, если
n = 4, а s0 = 10000
17

18.

Решение:
Динамической системой являются два
si
предприятия, состояния которых
r
определяются
вложенными
в 2 них
1
средствами, а управления u i = ui , ui на
k
ui
i-м году являются средствами ,
переданные k-й отраслью.
• Так
как
возвращённые
средства
распределяются полностью,
то имеет
1
2
место условие si -1 = ui + ui
2
1
• т.е. ui = si -1 - ui
и фактически задача
одномерна.
(
)

19.

Далее
будем считать, что управление на i1
м году определяется числами ui = ui , т.е.
средствами, выделенными первой отрасли.
В силу того же условия уравнения
состояний имеют вид:
si = F ( si -1 , ui ) = j1 (ui ) + j 2 ( si -1 - ui ) = 0,7ui + 0,9( si -1 - ui )
= 0,9 si -1 - 0,2ui
А
прибыль на i-м году равна:
f ( si -1 , ui ) = f1 (ui ) + f 2 ( si -1 - ui ) = 0,9ui + 0,8( si -1 - ui )
= 0,8si -1 + 0,1ui
19

20.

Решение
задачи начинается с оптимизации
функции z 3 ( s3 ) :
z 3 ( s3 ) = max f ( s3 , u4 ) = max f1 (u4 ) + f 2 ( s3 - u4 ) =
*
0 u 4 s3
max 0,8s3 + 0,1u4
0 u 4 s3
0 u 4 s3
Для
вычисления максимума заметим, что
требуется найти максимум линейной
функции на отрезке, поэтому:
*
*
z ( s3 ) = max 0,8s3 + 0,1u4 = 0,9 s3 при u 4 = s3
0 u s
3
4
3
si = 0,9 si -1 - 0,2ui
f ( si -1 , ui ) = 0,8si -1 + 0,1ui
20

21.

Далее,
z 2* ( s2 ) = max f ( s2 , u3 ) + z3* ( s3 ) = max 0,8s2 + 0,1u3 + 0,9 s3 =
0 u3 s 2
0 u3 s 2
= max 0,8s2 + 0,1u3 + 0,9(0,9 s2 - 0,2u3 ) =
0 u3 s 2
*
u
при 3 = 0
= max 0,81s2 - 0,18u3 = 0,81s2
0 u3 s 2
z1* ( s1 ) = max f ( s1 , u2 ) + z 2* ( s2 ) = max 0,8s1 + 0,1u2 + 0,81s2 =
0 u 2 s1
0 u 2 s1
= max 0,8s1 + 0,1u2 + 0,81(0,9 s1 - 0,2u2 ) =
0 u 2 s1
= max 0,249 s1 - 0,322u2 = 0,249 s1
0 u 2 s1
si = 0,9 si -1 - 0,2ui
при u2* = 0
f ( si -1 , ui ) = 0,8si -1 + 0,1ui

22.

z0* ( s0 ) = max f ( s0 , u1 ) + z1* ( s1 ) = max 0,8s0 + 0,1u1 + 0,249 s1 =
0 u1 s0
0 u1 s0
= max 0,8s0 + 0,1u1 + 0,249(0,9s0 - 0,2u1 ) =
0 u1 s0
= max 2,2841s0 - 0,3498u1 = 2,2841s0
0 u1 s0
*
u
при 1 = 0
Таким образом на первом шаге u4 = s3, т.е.
средства в четвёртом периоде вкладываются
только в первую отрасль, а на последующих
шагах средства вкладываются только во вторую
u
=
u
=
u
=
0
3
2
1
отрасль, т.к.
s1 = j1 ( s0 ) = 0,7 s0 = 7000
у.е.
s2 = j 2 ( s1 ) = 0,9 s1 = 6300
у.е.
s3 = j 2 ( s2 ) = 0,9 s2 = 5670
у.е.
f ( si -1 , ui ) = 0,8si -1 + 0,1ui
si = 0,9 si -1 - 0,2ui

23.

Максимальная
прибыль равна
*
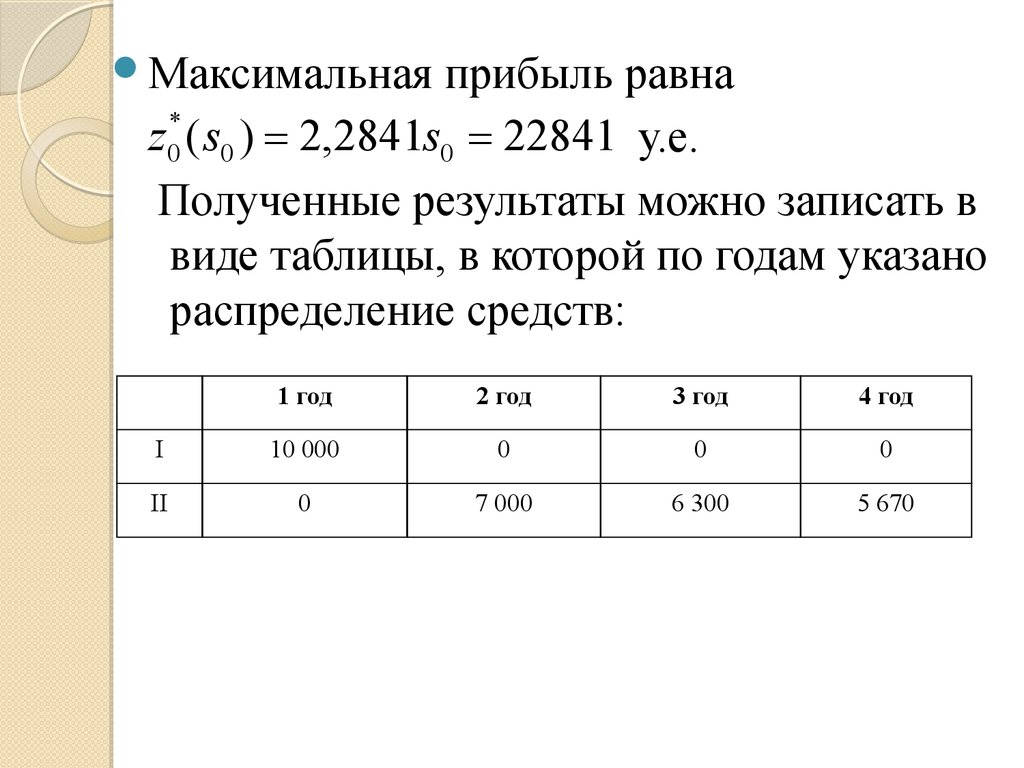
z0 ( s0 ) = 2,2841s0 = 22841 у.е.
Полученные результаты можно записать в
виде таблицы, в которой по годам указано
распределение средств:
1 год
2 год
3 год
4 год
I
10 000
0
0
0
II
0
7 000
6 300
5 670

24.

Рассмотрим
теперь
задачи
о
распределении
средств
между
несколькими предприятиями на один год.

25.

Задача 3
Планируется
работа n предприятий на один
год. Начальные средства равны S0 тыс. у.е.
При этом x тыс. у.е., вложенные в k-е
предприятие в начале года, дают в конце
года прибыль f (x) .
k
25

26.

Задача 3
Определить
оптимальный
план
распределения
средств
и
найти
максимальную прибыль, если s0 = 4 , n = 3, а
функции Fi (x) заданы в виде таблицы:
x
f1(x)
f2(x)
f3(x)
1
2
3
1
2
7
6
6
3
13
12
14
4
17
19
18
26

27.

Решение:
Шагом задачи будем считать выделение
средств очередному предприятию, а
переменные управления ui (i = 1, 2, 3) –
средства, выделеные i-му предпритятию.
• Таким образом, получаем следующую
задачу оптимизации:
z = f1 (u1 ) + f 2 (u2 ) + f 3 (u3 ) max
u1 + u2 + u3 = 4
ui 0, u Z , i = 1,2,3

28.

Состояние sk определяется количеством
оставшихся после k шагов средств
(средств, вкладываемых в инвестиции на
k–м шаге в предприятия с k-го по n-й).
• Уравнения состояний:
sk +1 = sk - uk

29.

1 этап. Условная оптимизация
1-й
шаг: для получения максимума
прибыли с последнего предприятия,
вложим в него все средства:
u3* = s3 , z3* ( s3 ) = f 3 ( s3 )
u3
0
1
2
3
4
z*3(s3)
u*3
0
0
-
-
-
-
0
0
1
-
1
-
-
-
1
1
2
-
-
6
-
-
6
2
3
-
-
-
14
-
14
3
4
-
-
-
-
18
18
4
s3
x
f1(x)
f2(x)
f3(x)
1
2
3
1
2
7
6
6
3
13
12
14
4
17
19
18
29

30.

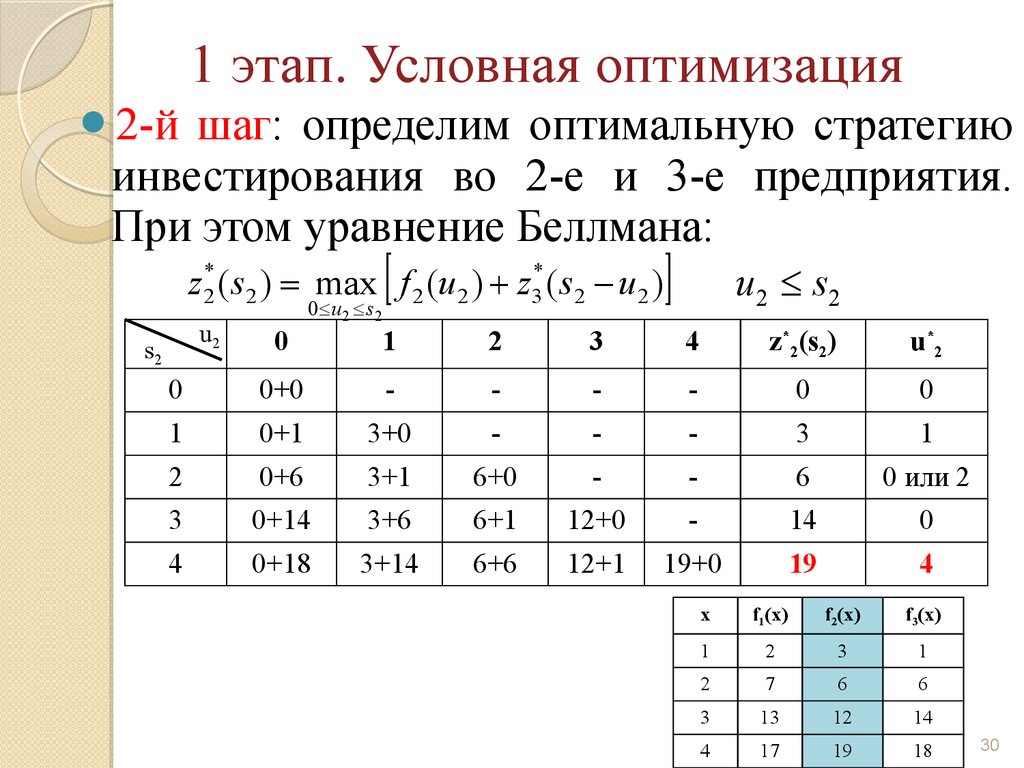
1 этап. Условная оптимизация
2-й
шаг: определим оптимальную стратегию
инвестирования во 2-е и 3-е предприятия.
При этом уравнение Беллмана:
z 2* ( s2 ) = max f 2 (u2 ) + z3* ( s2 - u2 )
u2
0 u 2 s 2
u 2 s2
0
1
2
3
4
z*2(s2)
u*2
0
0+0
-
-
-
-
0
0
1
0+1
3+0
-
-
-
3
1
2
0+6
3+1
6+0
-
-
6
0 или 2
3
0+14
3+6
6+1
12+0
-
14
0
4
0+18
3+14
6+6
12+1
19+0
19
4
s2
x
f1(x)
f2(x)
f3(x)
1
2
3
1
2
7
6
6
3
13
12
14
4
17
19
18
30

31.

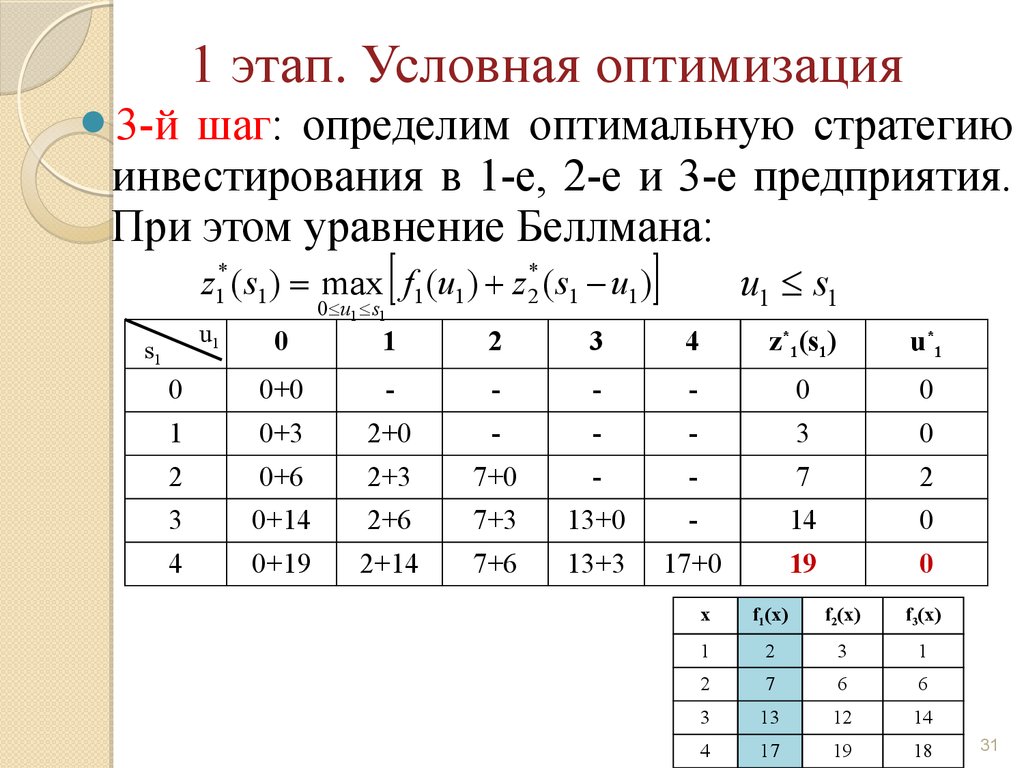
1 этап. Условная оптимизация
3-й
шаг: определим оптимальную стратегию
инвестирования в 1-е, 2-е и 3-е предприятия.
При этом уравнение Беллмана:
z1* ( s1 ) = max f1 (u1 ) + z2* ( s1 - u1 )
u1
0 u1 s1
u1 s1
0
1
2
3
4
z*1(s1)
u*1
0
0+0
-
-
-
-
0
0
1
0+3
2+0
-
-
-
3
0
2
0+6
2+3
7+0
-
-
7
2
3
0+14
2+6
7+3
13+0
-
14
0
4
0+19
2+14
7+6
13+3
17+0
19
0
s1
x
f1(x)
f2(x)
f3(x)
1
2
3
1
2
7
6
6
3
13
12
14
4
17
19
18
31

32.

2 этап. Безусловная оптимизация
1-й
шаг: максимальный доход при
инвестировании 4 тыс. у.е. между 3
*
z
предприятиями составляет: 1 (4) = 19
При
этом 1-му предприятию нужно
*
u
выделить
1 =0
тыс. у.е.
2-й
шаг: Определим величину оставшихся
денежных средств, приходящегося на долю
s1 -предприятий:
u1 = 4 - 0 = 4
2-гоs2и=3-го
тыс. у.е.
32

33.

2 этап. Безусловная оптимизация
По
данным 2-й таблицы оптимальный
вариант распределения денежных средств в
размере 4 тыс. у.е. между 2-м и 3-м
предприятиями составляет: z2* (4) = 19
При этом 2-му предприятию нужно выделить
u2* = 4 тыс. у.е.
3-й шаг: Определим величину оставшихся
денежных средств, приходящегося на долю
3-го предприятия:
s3 = s2 - u2 = 4 - 4 = 0 тыс. у.е.
33

34.

2 этап. Безусловная оптимизация
По
данным 1-й таблицы оптимальный вариант
распределения денежных средств в размере 0
тыс. у.е. для 3-го предприятия составляет:
При этом 3-му предприятию
*
нужно выделить
z3 (0) = 0
тыс. у.е.
Таким
образом,
оптимальный
план
u3* = 0
инвестирования
предприятий
,
обеспечивающий максимальный доход,* равный:
u = (0,4,0)
тыс. у.е.
z * (4) = f1 (0) + f 2 (4) + f 3 (0) = 0 + 19 + 0 = 19
34

35.

Задача 4
Планируется
работа n предприятий на один
год. Начальные средства равны S0 тыс. у.е.
При этом x тыс. у.е., вложенные в k-е
предприятие в начале года, дают в конце
года прибыль f k (x) .
35

36.

Задача 4
Определить
оптимальный
план
распределения
средств
и
найти
максимальную прибыль, если s0 = 4 , n = 3, а
функции Fi (x) заданы в виде таблицы:
x
f1(x)
f2(x)
f3(x)
1
4
3
5
2
7
8
9
3
11
12
13
4
20
16
17
36

37.

Решение:
Шагом задачи будем считать выделение
средств очередному предприятию, а
переменные управления ui (i = 1, 2, 3) –
средства, выделеные i-му предпритятию.
• Таким образом, получаем следующую
задачу оптимизации:
z = f1 (u1 ) + f 2 (u2 ) + f 3 (u3 ) max
u1 + u2 + u3 = 4
ui 0, u Z , i = 1,2,3

38.

Состояние sk определяется количеством
оставшихся после k шагов средств
(средств, вкладываемых в инвестиции на
k–м шаге в предприятия с k-го по n-й.
• Уравнения состояний:
sk +1 = sk - uk

39.

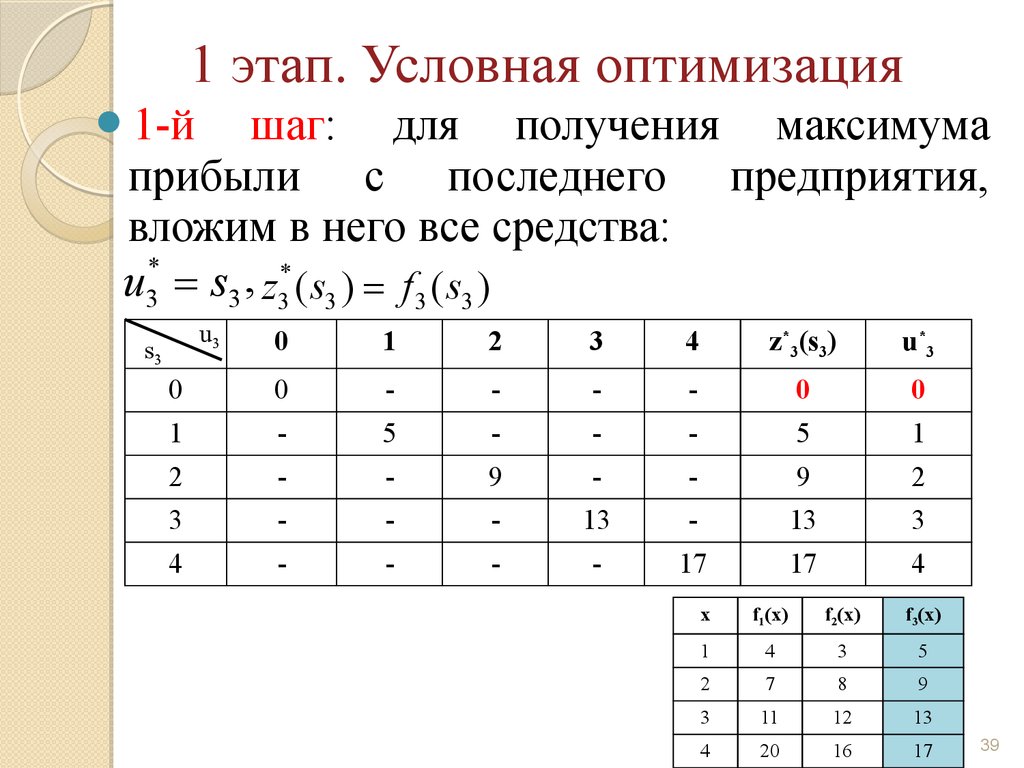
1 этап. Условная оптимизация
1-й
шаг: для получения максимума
прибыли с последнего предприятия,
вложим в него все средства:
u3* = s3 , z3* ( s3 ) = f 3 ( s3 )
u3
0
1
2
3
4
z*3(s3)
u*3
0
0
-
-
-
-
0
0
1
-
5
-
-
-
5
1
2
-
-
9
-
-
9
2
3
-
-
-
13
-
13
3
4
-
-
-
-
17
17
4
s3
x
f1(x)
f2(x)
f3(x)
1
4
3
5
2
7
8
9
3
11
12
13
4
20
16
17
39

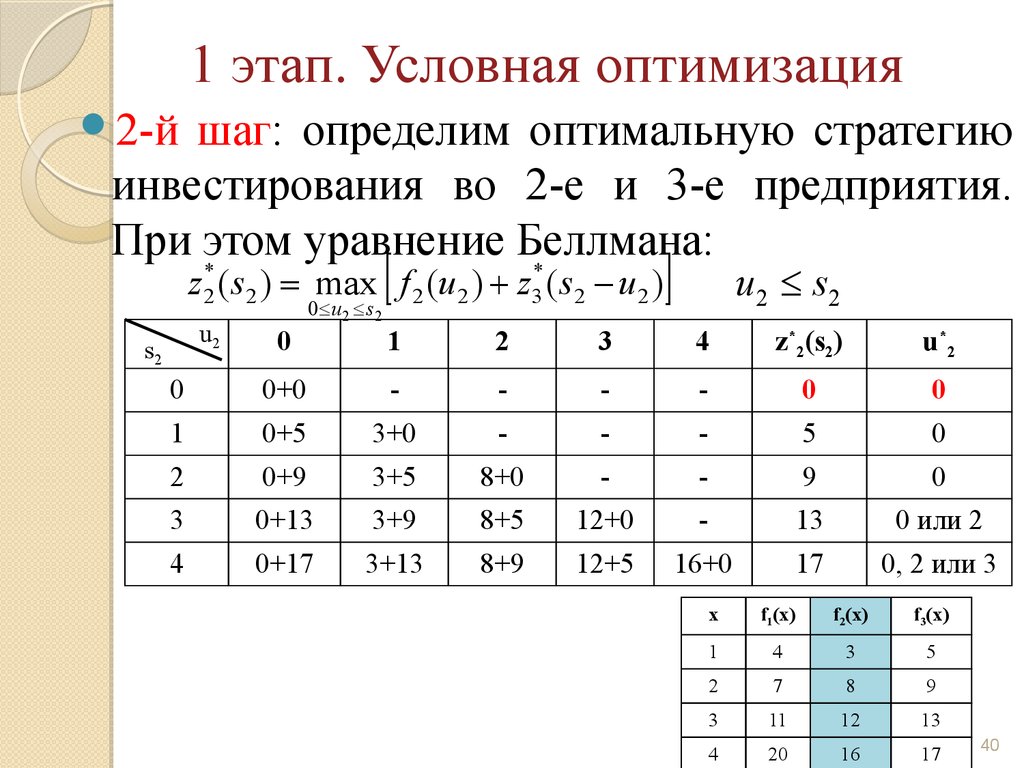
40.

1 этап. Условная оптимизация
2-й
шаг: определим оптимальную стратегию
инвестирования во 2-е и 3-е предприятия.
При этом уравнение Беллмана:
z 2* ( s2 ) = max f 2 (u2 ) + z3* ( s2 - u2 )
u2
0 u 2 s 2
u 2 s2
0
1
2
3
4
z*2(s2)
u*2
0
0+0
-
-
-
-
0
0
1
0+5
3+0
-
-
-
5
0
2
0+9
3+5
8+0
-
-
9
0
3
0+13
3+9
8+5
12+0
-
13
0 или 2
4
0+17
3+13
8+9
12+5
16+0
17
0, 2 или 3
s2
x
f1(x)
f2(x)
f3(x)
1
4
3
5
2
7
8
9
3
11
12
13
4
20
16
17
40

41.

1 этап. Условная оптимизация
3-й
шаг: определим оптимальную стратегию
инвестирования в 1-е, 2-е и 3-е предприятия.
При этом уравнение Беллмана:
z1* ( s1 ) = max f1 (u1 ) + z2* ( s1 - u1 )
u1
0 u1 s1
u1 s1
0
1
2
3
4
z*1(s1)
u*1
0
0+0
-
-
-
-
0
0
1
0+5
4+0
-
-
-
5
0
2
0+9
4+5
7+0
-
-
9
0 или 1
3
0+13
4+9
7+5
11+0
-
13
0 или 1
4
0+17
4+13
7+9
11+5
20+0
20
4
s1
x
f1(x)
f2(x)
f3(x)
1
4
3
5
2
7
8
9
3
11
12
13
4
20
16
17
41

42.

2 этап. Безусловная оптимизация
1-й
шаг: максимальный доход при
инвестировании 4 тыс. у.е. между 3
*
z
предприятиями составляет: 1 (4) = 20
При
этом 1-му предприятию нужно
*
u
выделить
1 =4
тыс. у.е.
2-й
шаг: Определим величину оставшихся
денежных средств, приходящегося на долю
s1 -предприятий:
u1 = 4 - 4 = 0
2-гоs2и=3-го
тыс. у.е.
42

43.

2 этап. Безусловная оптимизация
По
данным 2-й таблицы оптимальный
вариант распределения денежных средств в
размере 4 тыс. у.е. между 2-м и 3-м
предприятиями составляет: z2* (0) = 0
При этом 2-му предприятию нужно выделить
u2* = 0 тыс. у.е.
3-й шаг: Определим величину оставшихся
денежных средств, приходящегося на долю
3-го предприятия:
s3 = s2 - u2 = 0 - 0 = 0 тыс. у.е.
43

44.

2 этап. Безусловная оптимизация
По
данным 1-й таблицы оптимальный вариант
распределения денежных средств в размере 0
тыс. у.е. для 3-го предприятия составляет:
При этом 3-му предприятию
*
нужно выделить
z3 (0) = 0
тыс. у.е.
Таким
образом,
оптимальный
план
u3* = 0
инвестирования
предприятий
,
обеспечивающий максимальный доход,* равный:
u = (4,0,0)
тыс. у.е.
z * (4) = f1 (4) + f 2 (0) + f 3 (0) = 20 + 0 + 0 = 20
44

45. Методы оптимизации

Функция
спроса D(p) определяет спрос
(количество купленного товара) при цене p
за единицу продукции.
Функция предложения S(p) задает
количество товара, которое поставщик
может предложить по рыночной цене p.
45

46. Методы оптимизации

Говорят,
что рынок находится в равновесии,
если покупатели могут купить столько
товара, сколько им необходимо, а продавец
может реализовать весь товар, который он
намерен продать.
Равновесная цена р0 товара на рынке
находится из условия S(р0) = D(р0), а
количество q0 проданного товара q0 = D(р0).
46

47.

1. Оптимизация налогообложения
Предположим,
что на продукцию компании
вводится (дополнительный) фиксированный
налог t на каждую единицу реализованного
товара.
Если ставка налога достаточно велика, то
производство товара будет невыгодно, и это
приведет его к остановке.
Возникает вопрос о такой ставке налога,
чтобы итоговый сбор был максимальным.
47

48.

Задача 5
Пусть доход от продажи (выручка):
R (q ) = 54q - 4q 2
а затраты на выпуск продукта в зависимости от
количества q: 2
С (q ) = q - 6q + 24
Найти величину налога t на каждую единицу
продукта, чтобы налог T=tq от всей реализуемой
продукции был максимальным, и весь налоговый
сбор.
Как уменьшится количество выпускаемой
продукции?
48

49.

Решение:
Найдем
объем производства без учета
дополнительного налога.
Найдем функцию прибыли:
П (q ) = R (q ) - С (q ) = 54q - 4q 2 - q 2 + 6q - 24 =
= -5q 2 + 60q - 24
П 0 ' (q ) = -10q + 60 = 0
ее производной
находим, что максимум прибыли
достигается при объеме производства:
q0 = 6
Из

50.

По
причине введения дополнительного
налога доход производителя уменьшится на
величину Т = tq и составит
R (T ) (q ) = 54q - 4q 2 - tq
а его прибыль
П (q ) = R (T ) (q ) - С (q) = 54q - 4q 2 - tq - q 2 + 6q - 24 =
= -5q 2 + 60q - tq - 24

51.

В
результате компания исходит из того,
чтобы при реализации товара получить
максимальную прибыль.
Решим уравнение:
П ' (q ) = 60 - 10q - t = 0
q = 6 - t / 10
Общая
налоговая выплата составит:
T = tq = 6t - t 2 / 10

52.

T = tq = 6t - t 2 / 10
Вычислим максимум функции Т = T(t).
Из условия T’(t) = 0 следует, что
6-t /5 = 0
т.е. t = 30
Точка t = 30 является точкой максимума
функции T(t). При этом весь налоговый
сбор:
2
T (30) = 6 30 - 30 / 10 = 90

53.

Объем
производства:
q = 6 - 30 / 10 = 3
Таким образом, введение дополнительного
налога уменьшает объем производства в 2
раза (с 6 до 3 ед. продукции).
Ответ:
q0 = 6; t = 30; T (30) = 90; qt = 3

54.

Задача 6
Пусть доход от продажи (выручка):
R (q ) = 66q - 3q 2
а затраты на выпуск продукта в зависимости от
количества q: 2
С ( q) = q - 6q + 14
Найти величину налога t на каждую единицу
продукта, чтобы налог T=tq от всей реализуемой
продукции был максимальным, и весь налоговый
сбор.
Как уменьшится количество выпускаемой
продукции?
54

55.

Решение:
Найдем
объем производства без учета
дополнительного налога.
Найдем функцию прибыли:
П (q ) = R (q ) - С (q ) = 66q - 3q 2 - q 2 + 6q - 14 =
= -4q 2 + 72q - 14
П 0 ' (q ) = -8q + 72 = 0
ее производной
находим, что максимум прибыли
достигается при объеме производства:
q0 = 9
Из

56.

По
причине введения дополнительного
налога доход производителя уменьшится на
величину Т = tq и и составит
R (T ) (q ) = 66q - 3q 2 - tq
а его прибыль
П (q ) = R (T ) (q ) - С (q ) = 66q - 3q 2 - tq - q 2 + 6q - 14 =
= -4q 2 + 72q - tq - 14

57.

В
результате компания исходит из того,
чтобы при реализации товара получить
максимальную прибыль.
Решим уравнение:
П ' (q ) = 72 - 8q - t = 0
q = 9-t /8
Общая
налоговая выплата составит:
T = tq = 9t - t 2 / 8

58.

T = tq = 9t - t / 8
2
Вычислим
максимум функции Т = T(t).
Из условия T’(t) = 0 следует, что
9-t /4 = 0
т.е. t = 36
Точка t = 36 является точкой максимума
функции T(t). При этом весь налоговый
сбор:
2
T (36) = 9 36 - 36 / 8 = 162

59.

Объем
производства:
q = 9 - 36 / 8 = 4,5
Таким образом, введение дополнительного
налога уменьшает объем производства в 2
раза (с 9 до 4,5 ед. продукции).
Ответ:
q0 = 9; t = 36; T (36) = 162; qt = 4,5

60.

2. Оптимизация прибыли
Задача 7
Для товаров X1 и X2 известны функции спроса:
q1 = 54 - p1
1
q2 = 35 - p2
2
Фирма-монополист имеет функцию издержек:
2
2
С = 2q1 + 6q1q2 + 3q2 + 4
Вычислите максимальную прибыль фирмы в этих
условиях и найдите соответствующий
производственный план.
60

61.

Решение:
Найдем
цены товаров X1 и X2 :
p1 = 54 - q1
p2 = 70 - 2q2
Последовательно
находим общую выручку:
R (q1 , q2 ) = p1q1 + p2 q2 = (54 - q1 )q1 + (70 - 2q2 )q2 =
2
2
= -q1 - 2q2 + 54q1 + 70q2
Прибыль:
2
2
П (q1 , q2 ) = R (q1 , q2 ) - С (q1 , q2 ) = -3q1 - 5q2 + 54q1 +
+ 70q2 - 6q1q2 - 4

62.

Критические
точки функции П (q1 , q2 ) найдем
из системы:
П 'q1 = -6q1 - 6q2 + 54 = 0
П 'q2 = -6q1 - 10q2 + 70 = 0
Решением системы является точка (5;4).
Найдем матрицу вторых производных G(П)
функции П (q1 , q2 ) , которая не зависит от
точки:
П q''1q1
G ( П ) = ''
Пq q
21
П q''1q2 - 6 - 6
=
''
П q2 q2 - 6 - 10

63.

- 6 - 6
G (П ) =
- 6 - 10
имеет
угловые миноры
1 = -6 0, 2 = (-6) (-10) - (-6) 2 = 24 0
Поэтому точка (5;4) в силу выпуклости
функции прибыли, является точкой ее
глобального максимума и
П max = П (5,4) = -3 52 - 5 4 2 + 54 5 + 70 4 - 6 5 4 - 4 = 271
Ответ:
q1 = 5; q2 = 4; П max = 271

64.

Задача 8
Для товаров X1 и X2 известны функции спроса:
q1 = 50 - p1
1
q2 = 75 - p2
2
Фирма-монополист имеет функцию издержек:
2
2
С = 4q1 + 5q1q2 + 6q2 + 7
Вычислите максимальную прибыль фирмы в этих
условиях и найдите соответствующий
производственный план.
64

65.

Решение:
Найдем
цены товаров X1 и X2 :
p1 = 50 - q1
p2 = 150 - 2q2
Последовательно
находим общую выручку:
R (q1 , q2 ) = p1q1 + p2 q2 = (50 - q1 )q1 + (150 - 2q2 )q2 =
2
2
= - q1 - 2q2 + 50q1 + 150q2
Прибыль:
2
2
П (q1 , q2 ) = R (q1 , q2 ) - С (q1 , q2 ) = -5q1 - 8q2 + 50q1 +
+ 150q2 - 5q1q2 - 7

66.

Критические
точки функции П (q1 , q2 ) найдем
из системы:
П 'q1 = -10q1 - 5q2 + 50 = 0
П 'q2 = -5q1 - 16q2 + 150 = 0
Решением
системы является точка:
10
250
q1 =
, q2 =
27
27
Найдем
матрицу вторых производных G(П)
функции П (q1 , q2 ) , которая не зависит от
точки:
П q'' q П q'' q - 10 - 5
G ( П ) = '' 1 1
Пq q
21
1 2
П
''
q2 q2
=
- 5
- 16

67.

- 10 - 5
G (П ) =
- 5 - 16
имеет
угловые миноры
1 = -10 0, 2 = (-10) (-16) - (-5) 2 = 135 0
Поэтому
точка
10
250
q1 =
, q2 =
27
27в силу выпуклости
функции прибыли, является точкой ее глобального
максимума и
2
2
10
10 250
10
250
П max = П ,
= -5 - 8
+ 50 +
27
27 27
27
27
250
10 250
18811
+ 150
- 5
-7 =
27
27 27
27

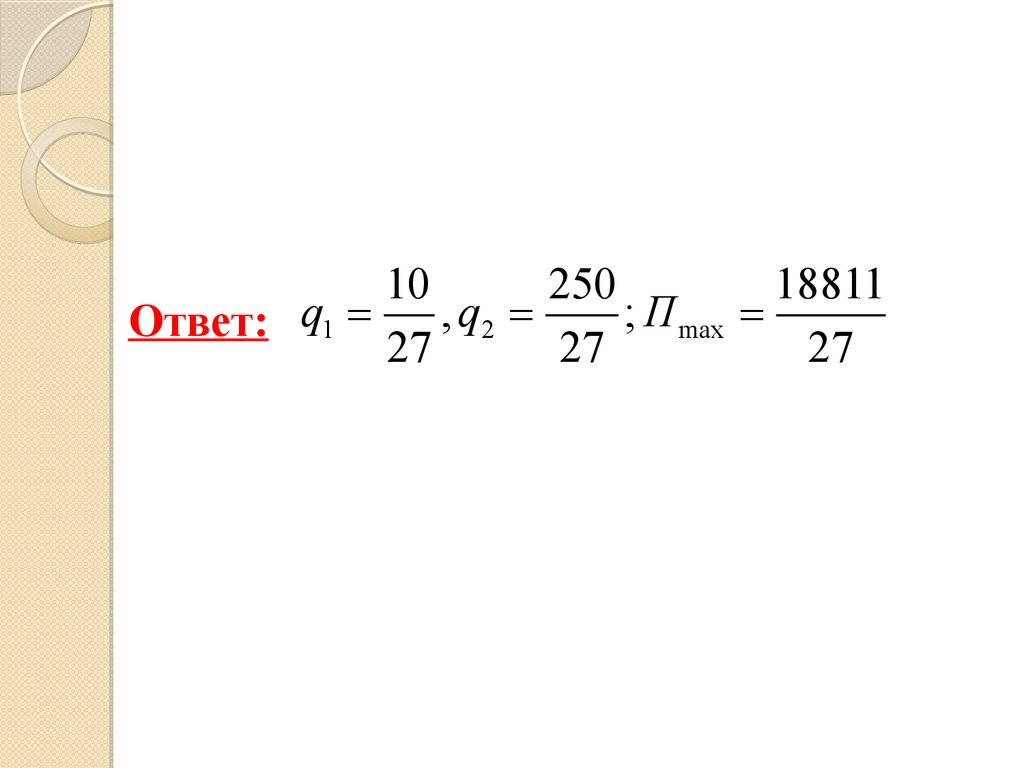
68.

10
250
18811
, q2 =
; П max =
Ответ: q1 =
27
27
27

69. Задачи многокритериальной оптимизации

Задача
вида:
f i ( x) max(min),
x D,
где i > 1, D R n- допустимое множество;
fi(x) – гладкие функции на D, называется
задачей многокритериальной оптимизации.
Область допустимых решений D задается
системой уравнений и неравенств.
69

70.

Пусть
X и Y – два допустимых решения.
Говорят, что X доминирует Y, если для всех
i = 1, 2, …, n выполняется неравенство
fi(X) ≥ fi(Y) и найдется такое k, что fk(X) >
fk(Y).
Решение Z называется недоминируемым
(эффективным), если нет решения X,
которое бы доминировало Z.
70

71.

Множество
эффективных
(недоминируемых) решений называется
множеством Парето.
Геометрическое изображение множества
Парето называется Парето-эффективной
границей (Парето-оптимальной границей).
В задаче многокритериальной оптимизации
наилучшее решение следует искать в
множестве Парето.
71

72.

Алгоритм
построения Парето-эффективной
границы:
1. Строим допустимое множество D, заданное
системой ограничений как пересечение
полуплоскостей, соответствующих каждому
неравенству, входящему в эту систему.
2. Для каждой функции f i = ci1 x1 + ci 2 x2 + ci 0
строим линию уровня как прямую,
перпендикулярную соответствующему
вектору нормали ni = (ci1 , ci 2 ) .
72

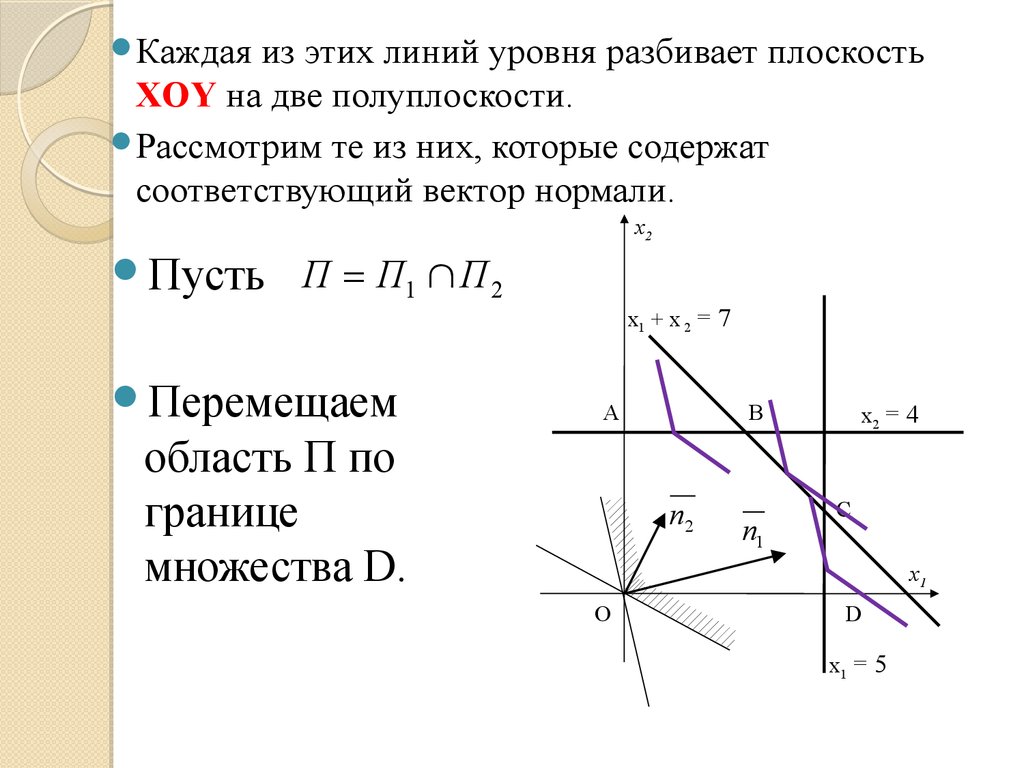
73.

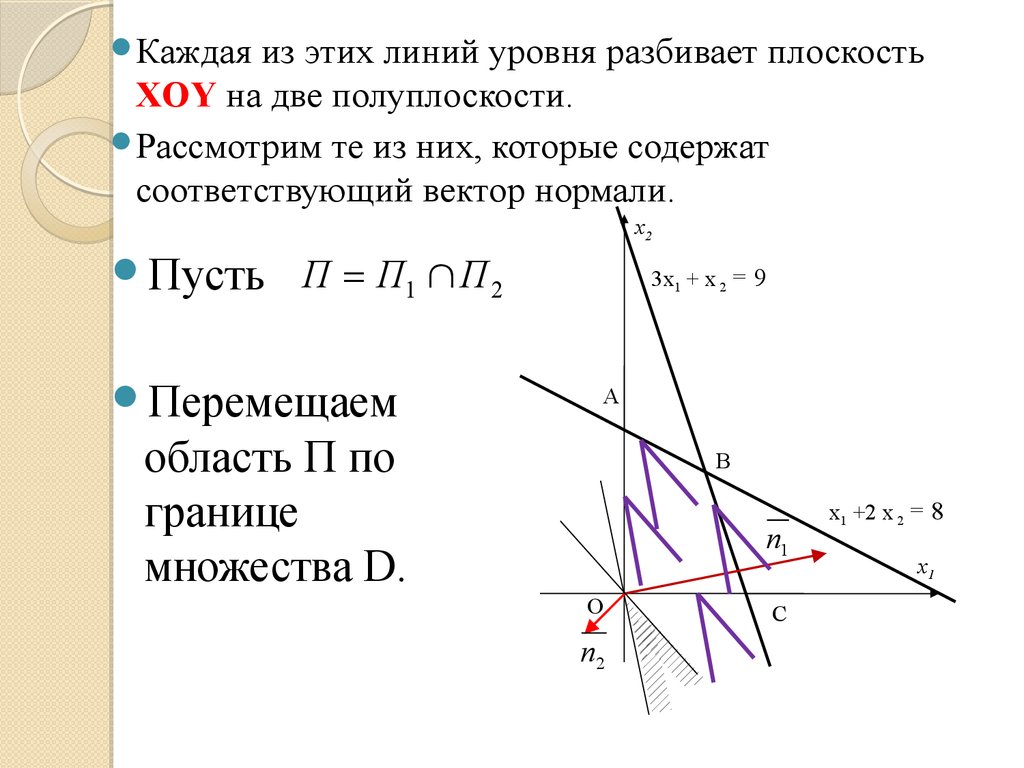
Каждая
из этих линий разбивает плоскость
XOY на две полуплоскости.
Пусть Пi – полуплоскости, содержащие вектор
градиента целевойn функции fi, а их пересечение
П = Пi
i =1
3. Перемещая данную область П по границе
допустимого множества D, находим те точки
границы, которые являются единственными
точками пересечения областей П и D.
Данные точки - оптимальные по Парето, а
множество всех таких точек – Паретоэффективная граница.
73

74.

Задача 9
Найти
задачи:
Парето-эффективную
границу
f1 = 4 x1 + x2 max
f = x + 2 x max
1
2
2
x1 + x2 7
x1 5
x 4
2
x1 0
x2 0
74

75.

Решение:
По
условию задачи область допустимых
решений задана системой неравенств:
x1 + x2 7
x 5
1
x2 4
x 0
1
x2 0
Построим
данную область:
x1 + x2 = 7
x1 = 5
x = 4
2

76.

В
качестве допустимого множества получаем
область ОАВСD с угловыми точками О(0;0),
А(0;4), В(3;4), С(5;2), D(5;0).
Для
функций f1 и f2
построим линии
уровня (f1 = const,
f2 = const) как
прямые,
перпендикулярные
соответствующим
векторам нормали
n1 = (4;1)
n2 = (1;2)
x2
x1 + x 2 = 7
А
В
n2
n1
x2 = 4
C
x1
O
D
x1 = 5

77.

Каждая
из этих линий уровня разбивает плоскость
XOY на две полуплоскости.
Рассмотрим те из них, которые содержат
соответствующий вектор нормали.
x2
Пусть
П = П1 П 2
x1 + x 2 = 7
Перемещаем
А
область П по
границе
множества D.
В
n2
n1
x2 = 4
C
x1
O
D
x1 = 5

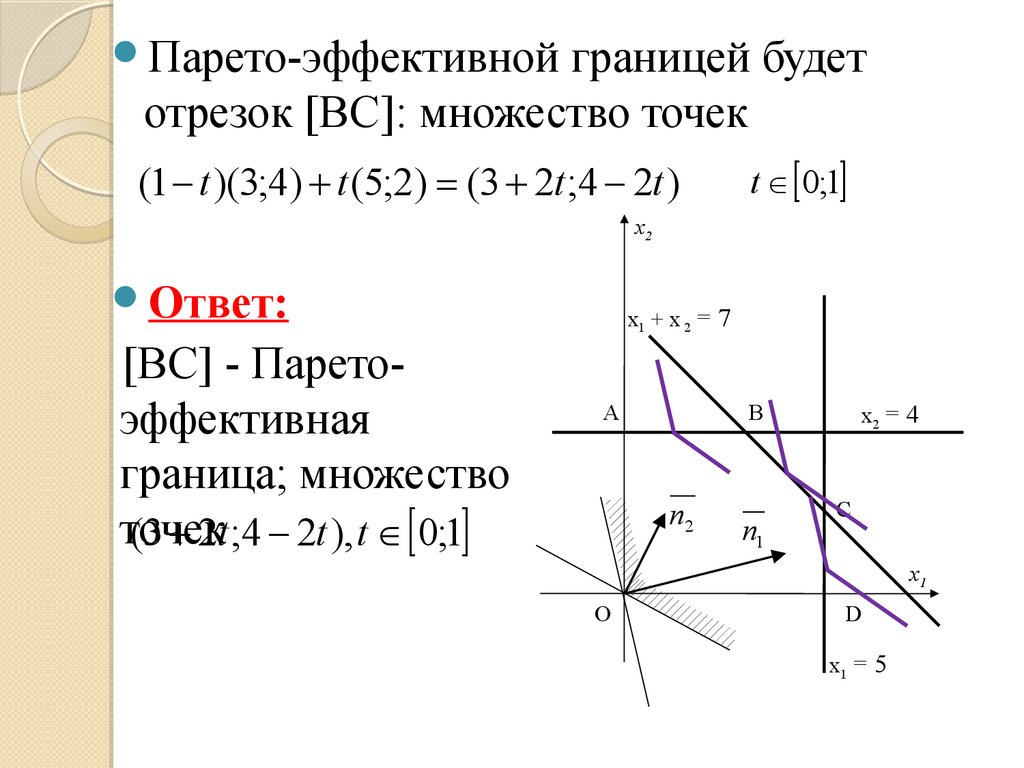
78.

Парето-эффективной
границей будет
отрезок [BC]: множество точек
t 0;1
(1 - t )(3;4) + t (5;2) = (3 + 2t ;4 - 2t )
x2
Ответ:
[BC] - Паретоэффективная
граница; множество
точек
(3 + 2t ;4 - 2t ), t 0;1
x1 + x 2 = 7
А
В
n2
n1
x2 = 4
C
x1
O
D
x1 = 5

79.

Задача 10
Найти
задачи:
Парето-эффективную
границу
f1 = x1 + 5 x2 max
f = x + x min
1
2
2
x1 + 2 x2 8
3 x1 + x2 9
x1 0
x2 0
79

80.

Решение:
По
условию задачи область допустимых
решений задана системой неравенств:
x1 + 2 x2 8
3 x + x 9
1 2
x1 0
x2 0
Построим
x1 + 2 x2 = 8
3 x1 + x2 = 9
f1 = x1 + 5 x2 max
f 2 = - x1 - x2 max
данную область:

81.

В
качестве допустимого множества
получаем область ОАВС с угловыми
точками О(0;0), А(0;4), В(2;3), С(3;0).
x
Для функций f1 и f2
3x + x = 9
построим линии
уровня (f1 = const,
А
f2 = const) как
В
прямые,
x +2 x
перпендикулярные
n
соответствующим
O
C
векторам нормали
n
2
1
2
1
1
n1 = (1;5) n2 = (-1;-1)
2
2
=8
x1

82.

Каждая
из этих линий уровня разбивает плоскость
XOY на две полуплоскости.
Рассмотрим те из них, которые содержат
соответствующий вектор нормали.
x2
Пусть
П = П1 П 2
Перемещаем
3x1 + x 2 = 9
А
область П по
границе
множества D.
В
n1
O
n2
C
x1 +2 x 2 = 8
x1

83.

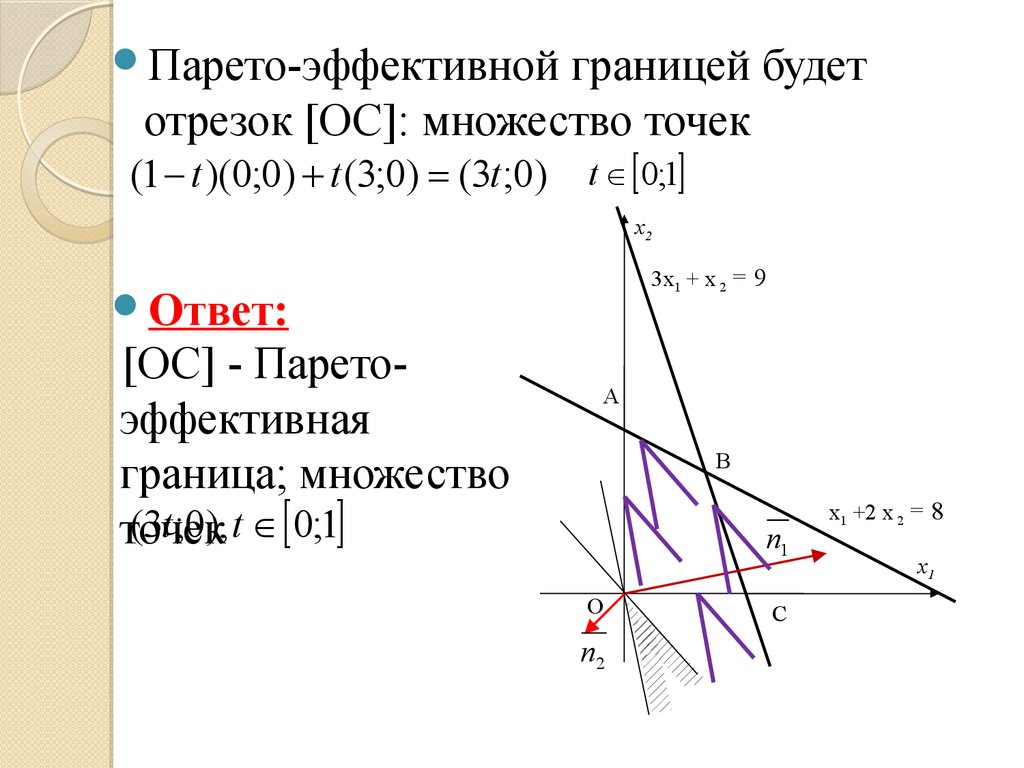
Парето-эффективной
границей будет
отрезок [OС]: множество точек
(1 - t )(0;0) + t (3;0) = (3t ;0) t 0;1
x2
3x1 + x 2 = 9
Ответ:
[OС] - Паретоэффективная
граница; множество
(3t ;0), t 0;1
точек
А
В
n1
O
n2
C
x1 +2 x 2 = 8
x1

84. Метод идеальной точки

Метод
идеальной точки является
геометрическим методом для
многокритериальных задач.
84

85.

Задача 11
Решить задачу многокритериальной
оптимизации методом идеальной точки:
f1 = x1 + 3 x2 max
f = 2 x + x max
1
2
2
- x1 + x2 3
x1 + x2 10
x1 8
x2 5
x1 0
x 0
2
85

86.

Решение:
По
условию задачи область допустимых
решений задана системой неравенств:
- x1 + x2 3
x + x 10
1 2
x1 8
x2 5
x1 0
x2 0
Построим
данную область:
- x1 + x2 = 3
x + x = 10
1 2
x1 = 8
x2 = 5

87.

В
качестве допустимого множества получаем
область ОАВСDЕ с угловыми точками О(0;0),
А(0;3), В(2;5), С(5;5), D(8;2), Е(8;0).
Введем
линейное
преобразование f:
R 2 R 2, определенное
критериями f1 и f2:
f1 ( x)
=
f ( x) =
f 2 ( x)
x1 + 3x2 1 3 x1
=
=
2 x1 + x2 2 1 x2
x2
- x1 + x 2 = 3
x1 + x 2 = 10
В
C
x2 = 5
А
D
x1
O
Е
x1 = 8

88.

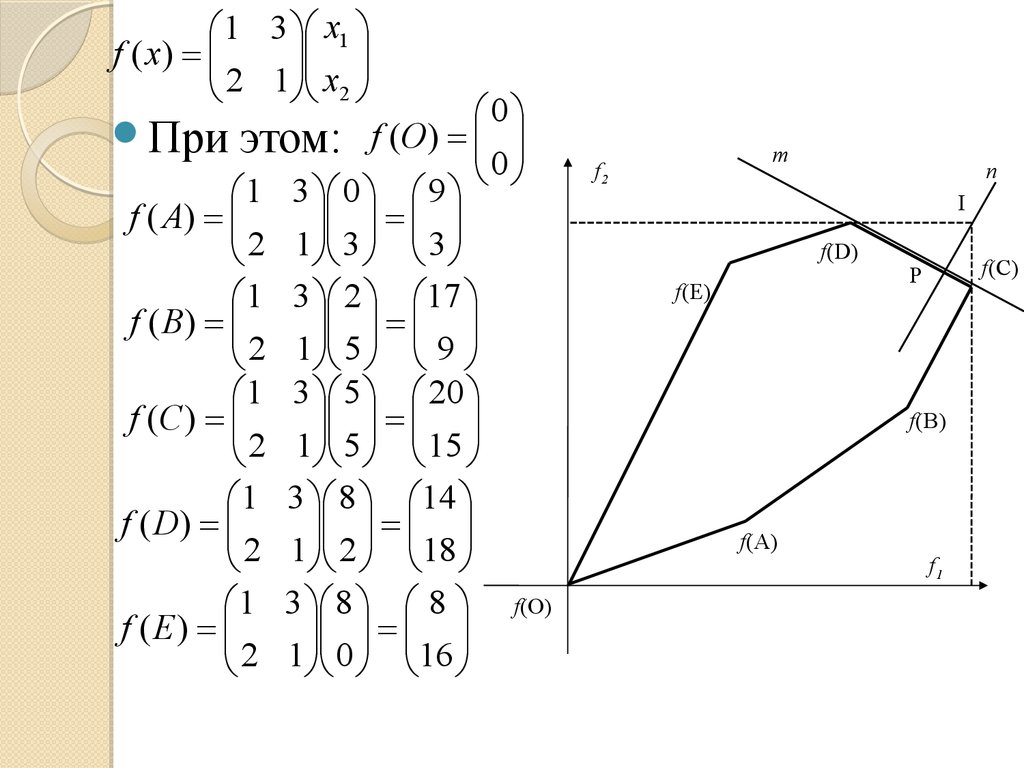
1 3 x1
f ( x) =
2 1 x2
0
При этом: f (О) =
0
1 3 0 9
=
f ( А) =
2 1 3 3
1 3 2 17
=
f (В) =
2 1 5 9
1 3 5 20
=
f (С ) =
2 1 5 15
1 3 8 14
=
f (D) =
2 1 2 18
1 3 8 8 f(O)
=
f (E ) =
2 1 0 16
m
f2
n
I
f(D)
f(E)
f(C)
P
f(В)
f(А)
f1

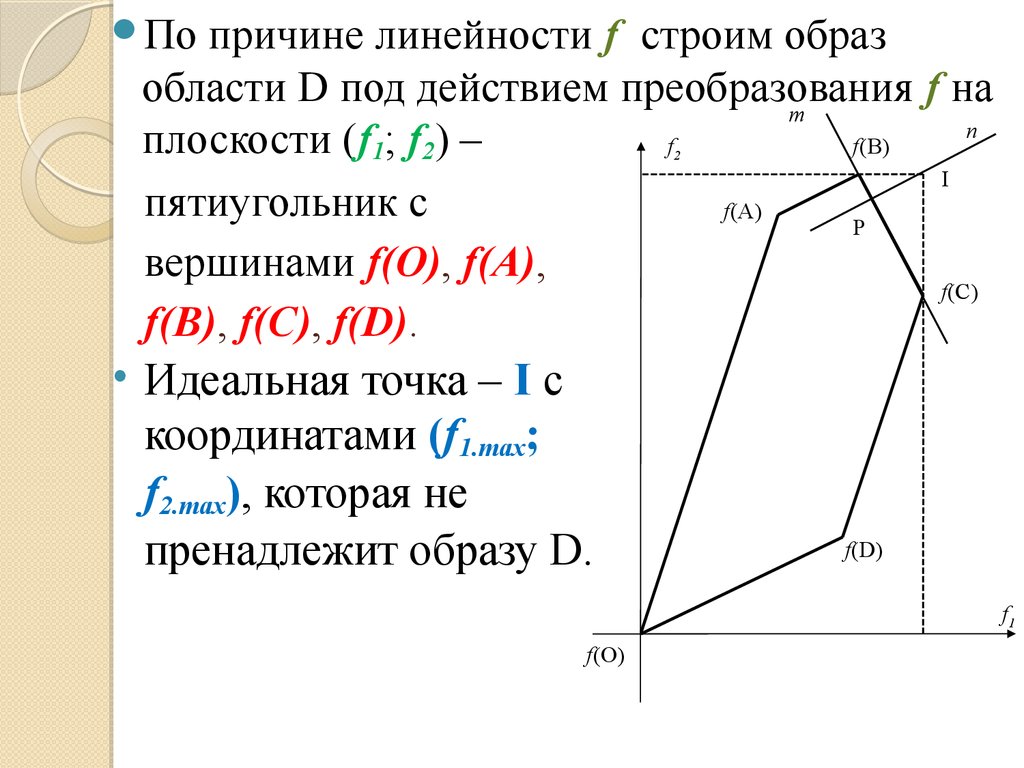
89.

По
причине линейности f строим образ
области D под действием преобразования f
m
n
на плоскости (f1; f2) – f
I
шестиугольник с
f(D)
f(C)
P
f(E)
вершинами f(О), f(А),
f(В), f(С), f(D), f(E).
f(В)
• Идеальная точка – I
с координатами
f(А)
(f1.max; f2.max), которая
f
не пренадлежит f(O)
образу D.
2
1

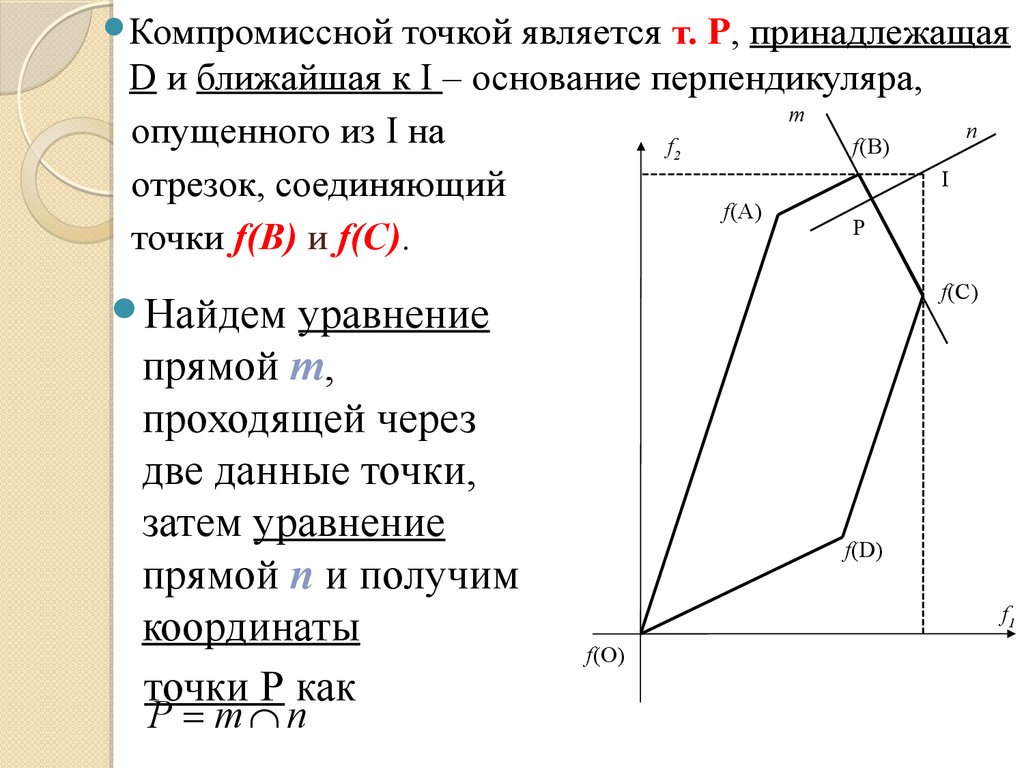
90.

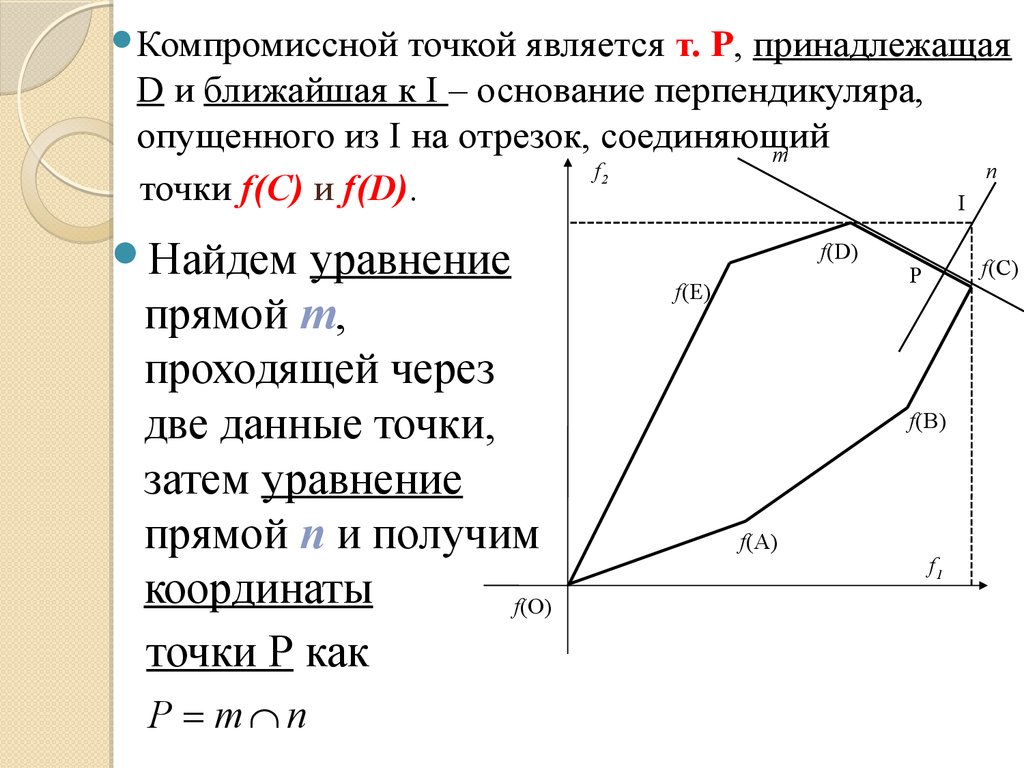
Компромиссной
точкой является т. Р, принадлежащая
D и ближайшая к I – основание перпендикуляра,
опущенного из I на отрезок, соединяющий
m
f
n
точки f(С) и f(D).
I
2
Найдем
уравнение
прямой m,
проходящей через
две данные точки,
затем уравнение
прямой n и получим
координаты
f(O)
точки Р как
P = m n
f(D)
f(E)
f(C)
P
f(В)
f(А)
f1

91.

20
f (С ) =
15
14
f (D ) =
18
Уравнение прямой m:
f1 - 14 f 2 - 18
=
20 - 14 15 - 18
3 f1 + 6 f 2 = 150
Уравнение нормали:
20
I =
18
m
f2
I
f(D)
f(E)
n = (3;6)
Уравнение прямой n:
f1 - 20 f 2 - 18
=
3
6
f(O)
6 f1 - 3 f 2 = 66
n
f(C)
P
f(В)
f(А)
f1

92.

Решим
систему уравнений:
3 f1 + 6 f 2 = 150
6 f1 - 3 f 2 = 66
f1 = 50 - 2 f 2
6(50 - 2 f 2 ) - 3 f 2 = 66
Найдем
f 2 = 15,6
f1 = 18,8
компромиссную точку как прообраз
Р: f1 = x1 + 3x2
x1 + 3x2 = 15,6
2 x1 + x2 = 18,8
f 2 = 2 x1 + x2
x1 = 5,6
x2 = 4,4
Ответ: X * = (5,6;4,4); f * = (18,8;15,6)

93.

Задача 12
Решить задачу многокритериальной
оптимизации методом идеальной точки:
f1 = 2 x1 + x2 max
f = x + 3 x max
1
2
2
x1 + x2 9
x1 5
x 7
2
x1 0
x2 0
93

94.

Решение:
По
условию задачи область допустимых
решений задана системой неравенств:
x1 + x2 9
x 5
1
x2 7
x 0
1
x2 0
Построим
данную область:
x1 + x2 = 9
x1 = 5
x = 7
2

95.

В
качестве допустимого множества получаем
область ОАВСD с угловыми точками О(0;0),
А(0;7), В(2;7), С(5;4), D(5;0).
линейное
преобразование f:
R 2 R 2, определенное
критериями f1 и f2:
x2
Введем
f1 ( x)
=
f ( x) =
f 2 ( x)
2 x1 + x2 2 1 x1
=
=
x1 + 3x2 1 3 x2
В
x2 = 7
А
C
x1 + x 2 = 9
D
O
x1 = 5
x1

96.

2 1 x1
f ( x) =
1 3 x2
0
При этом: f (О) =
2
f ( А) =
1
2
f (В ) =
1
2
f (С ) =
1
1 0 7
=
3 7 21
m
f2
0
n
f(В)
I
f(А)
P
f(C)
1 2 11
=
3 7 23
1 5 14
=
3 4 17
2 1 5 10
=
f (D ) =
1 3 0 5
f(D)
f1
f(O)

97.

По
причине линейности f строим образ
области D под действием преобразования
f
на
m
n
плоскости (f1; f2) –
f
f(В)
I
пятиугольник с
f(А)
P
вершинами f(О), f(А),
f(C)
f(В), f(С), f(D).
2
• Идеальная точка – I с
координатами (f1.max;
f2.max), которая не
пренадлежит образу D.
f(D)
f1
f(O)

98.

Компромиссной
точкой является т. Р, принадлежащая
D и ближайшая к I – основание перпендикуляра,
m
n
опущенного из I на
f
f(В)
I
отрезок, соединяющий
f(А)
P
точки f(В) и f(С).
2
уравнение
прямой m,
проходящей через
две данные точки,
затем уравнение
прямой n и получим
координаты
точки Р как
f(C)
Найдем
P = m n
f(D)
f1
f(O)

99.

11
f (В ) =
23
14
f (С ) =
17
14
I =
23
Уравнение прямой m:
f1 - 11 f 2 - 23
=
14 - 11 17 - 23
2 f1 + f 2 = 45
Уравнение нормали:
m
f2
n
f(В)
I
f(А)
P
f(C)
n = (2;1)
Уравнение прямой
f1 - 14 f 2 - 23
=
2
1
f1 - 2 f 2 = -32
n:
f(D)
f1
f(O)

100.

Решим
систему уравнений:
2 f1 + f 2 = 45
f1 - 2 f 2 = -32
f1 = -32 + 2 f 2
2(-32 + 2 f 2 ) + f 2 = 45
Найдем
f 2 = 21,8
f1 = 11,6
компромиссную точку как прообраз
Р: f1 = 2 x1 + x2
2 x1 + x2 = 11,6
x1 + 3x2 = 21,8
f 2 = x1 + 3 x2
x1 = 2,6
x2 = 6,4
Ответ: X * = (2,6;6,4); f * = (11,6;21,8)

101. Спасибо за внимание!