БМ-02-25 (2)

1.

Кейс: Оптимизация времени отклика сервера
• Дисциплина: Высшая математика
• Выполнил(а): Батыров Муслим
• Группа: 02-25

2.

Описание кейса
• Цель исследования: Анализ зависимости времени отклика
сервера от количества входящих запросов.
• Практическая значимость:
• - Определение оптимальной нагрузки
• - Прогноз деградации
• - Планирование масштабирования
• Исходная функция:
• f(x) = (x² + 3x + 1) / (x² + 1)

3.

Роль производной
Производная показывает скорость изменения времени отклика.
f'(x) > 0 — растет
f'(x) < 0 — уменьшается
f'(x) = 0 — экстремум
• Нужно для поиска оптимальной нагрузки.

4.

Нахождение производной
• f(x) = (x² + 3x + 1) / (x² + 1)
• f'(x) = [(2x + 3)(x² + 1) - (x² + 3x + 1)(2x)] / (x² + 1)²
• f'(x) = 3(1 - x²)/(x² + 1)²

5.

Критические точки
• 3(1 - x²)/(x² + 1)² = 0
• x = ±1
• (-∞,-1) — убывает
• (-1,1) — возрастает
• (1,+∞) — убывает

6.

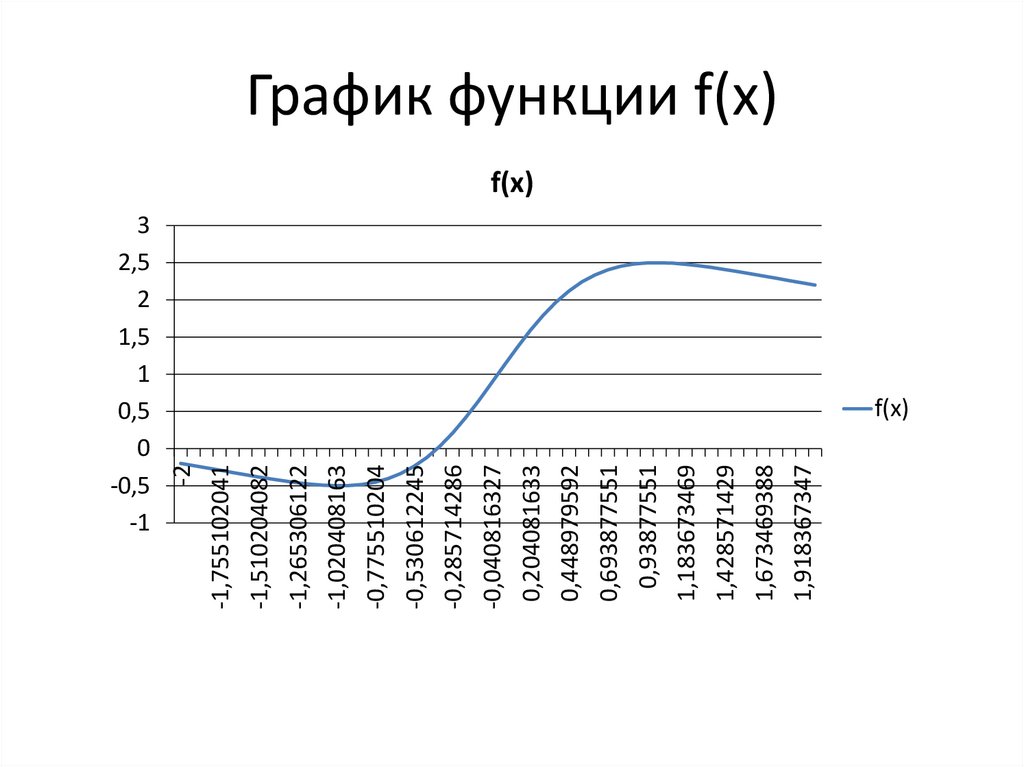
График f(x)
• Экстремумы:
• x = -1 → f(x) = -0.5 (минимум)
• x = 1 → f(x) = 2.5 (максимум)
• Асимптота: y = 1

7.

График f'(x)
• f'(x) > 0 на (-1,1)
• f'(x) < 0 вне этого интервала
• Нули производной соответствуют экстремумам функции

8.

Итоговая таблица
Область определения: (-∞,+∞)
Критические точки: x=-1, x=1
Минимум: (-1,-0.5)
Максимум: (1,2.5)
Асимптота: y=1

9.

Интерпретация
При x от 0 до 1 время отклика растет
После x=1 модель показывает снижение
Это упрощённая математическая модель
Реальная система имеет предел производительности

10.

Выводы
1. Глобальный минимум: x=-1 (теоретически)
2. Практически лучший режим: x=0
3. Производная помогает искать узкие места
4. Модель требует проверки на реальных данных

11.

График функции f(x)

12.

3
2,5
2
1,5
1
0,5
0
-0,5
-1
1,918367347
1,673469388
1,428571429
1,183673469
0,93877551
0,693877551
0,448979592
0,204081633
-0,040816327
-0,285714286
-0,530612245
-0,775510204
-1,020408163
-1,265306122
-1,510204082
-1,755102041
-2
График функции f(x)
f(x)
f(x)