ОСН_ТЕОРЕМЫ_И_ИССЛ_ФУНКЦИЙ20201_лекции_9,10_1

1. Исследование функций и построение графиков

2. Исследование функций

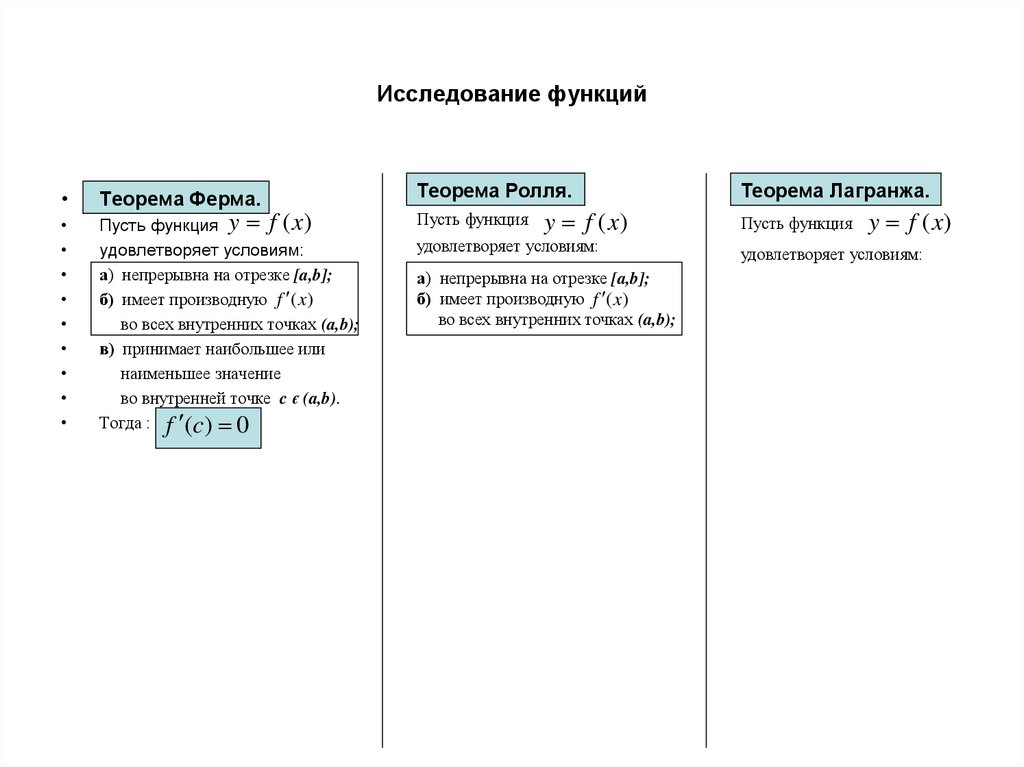
Теорема Ферма.
Теорема Ролля.
Теорема Лагранжа.

3. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
Теорема Ролля.
Теорема Лагранжа.

4. Исследование функций

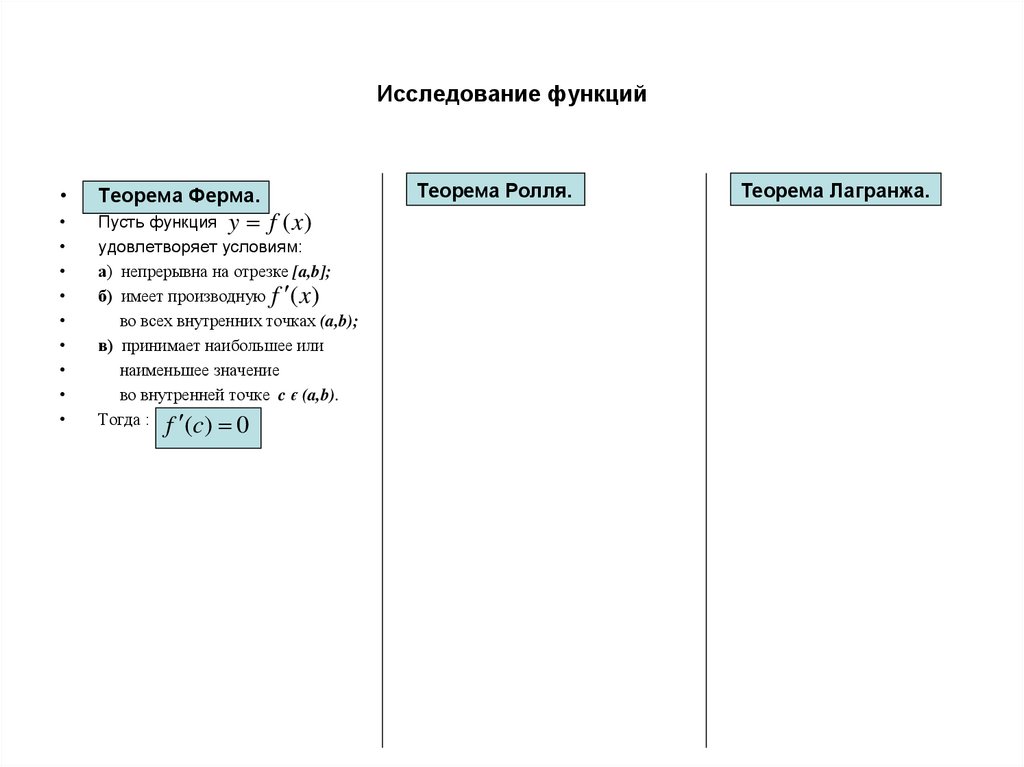
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Теорема Лагранжа.

5. Исследование функций

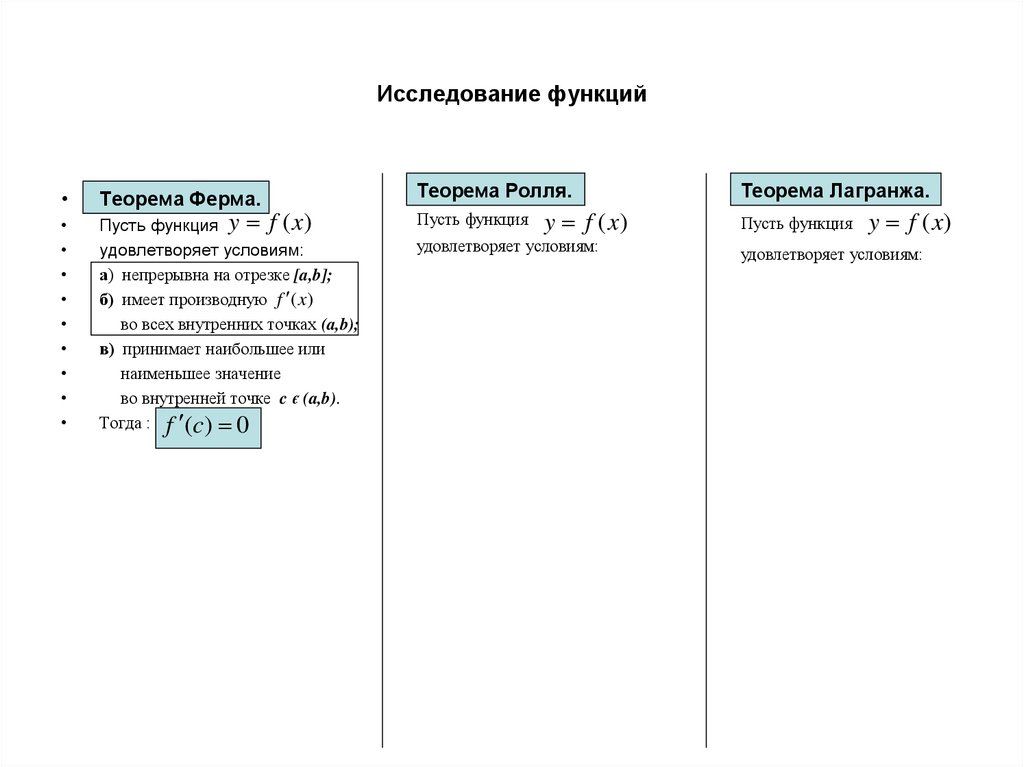
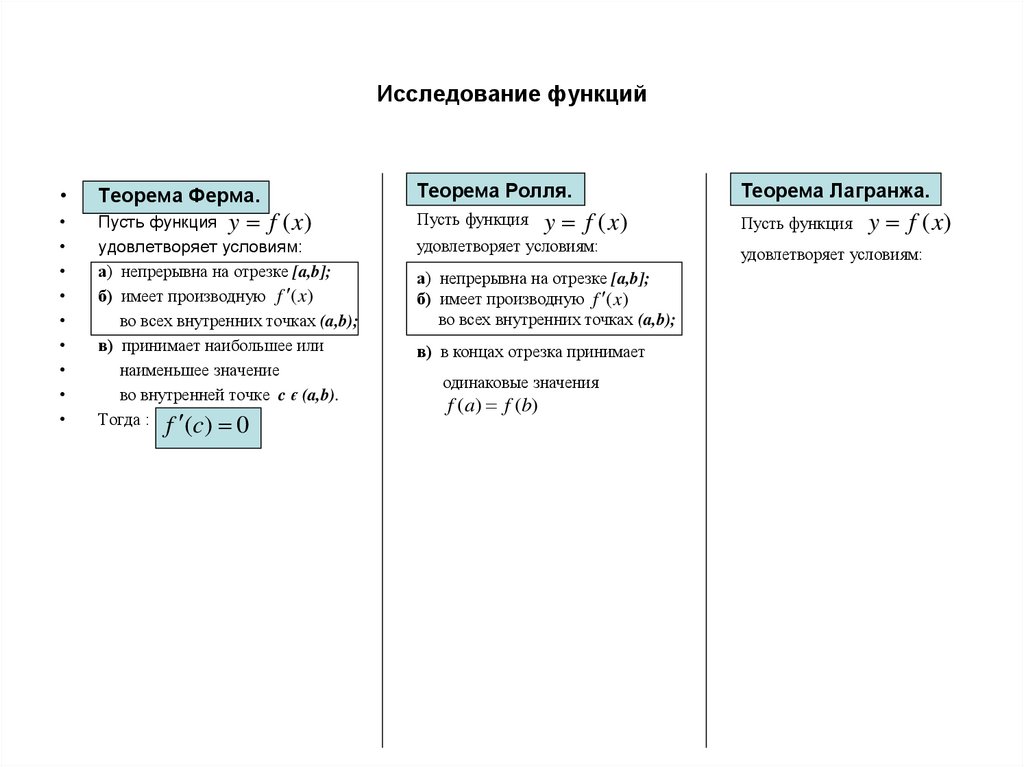
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

6. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

7. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

8. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
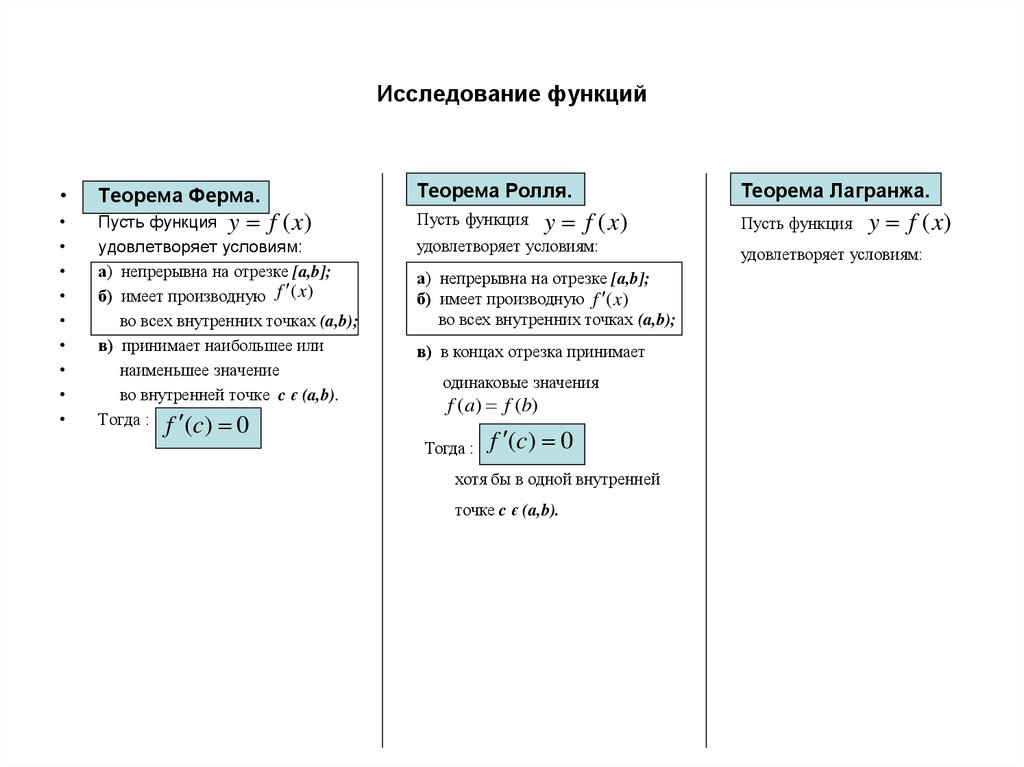
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

9. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
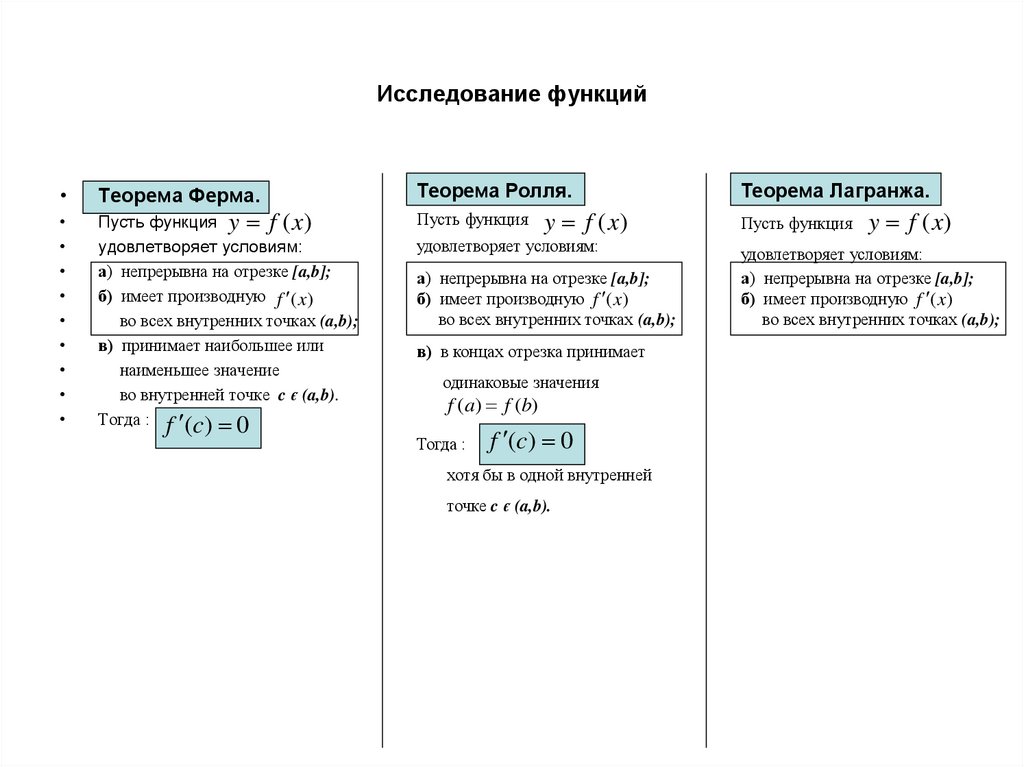
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);

10. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
Тогда :
f (c)
f (b) f (a)
b a
хотя бы в одной внутренней
точке c є (a,b).

11. Исследование функций

Теорема Ролля.
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
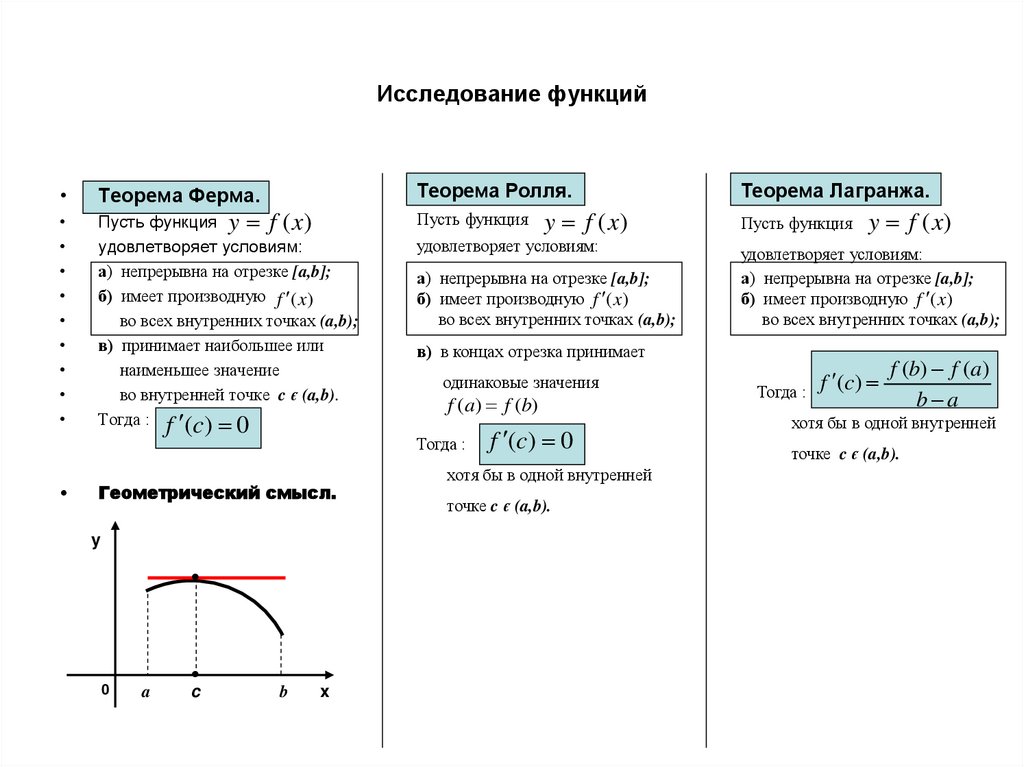
Геометрический смысл.
y
0
a
c
b
x
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
Тогда :
f (c)
f (b) f (a)
b a
хотя бы в одной внутренней
точке c є (a,b).

12. Исследование функций

Теорема Ролля.
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
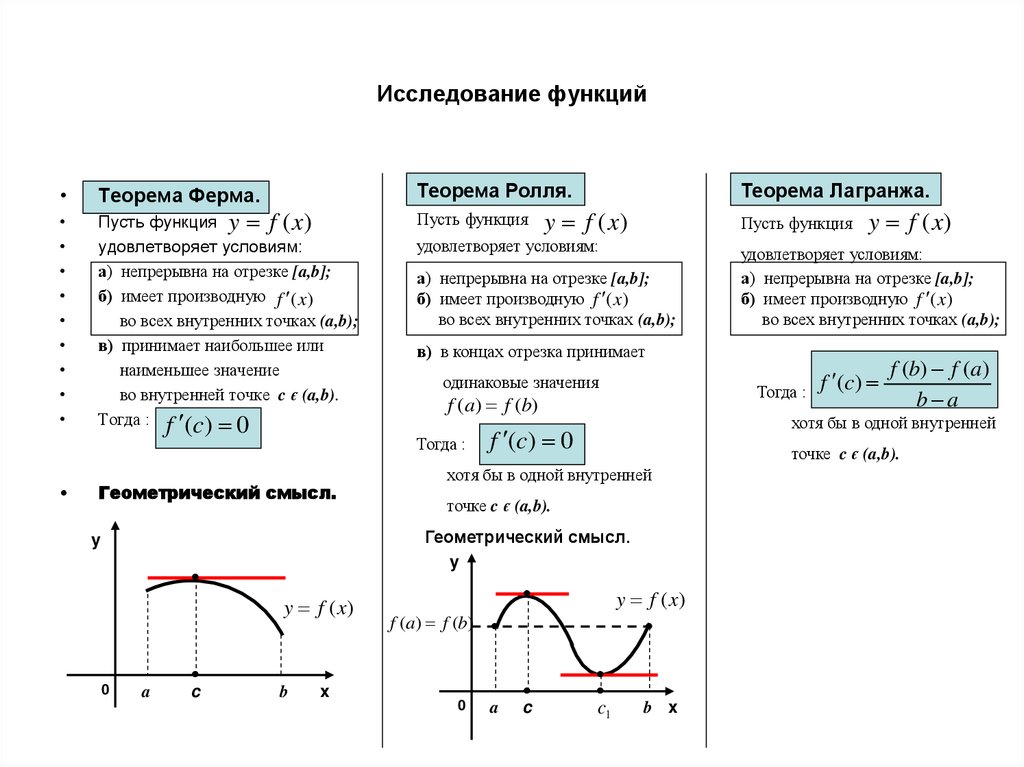
Геометрический смысл.
y f (x)
a
c
y f (x)
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
b
x
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
f (a) f (b)
Тогда :
точке c є (a,b).
y f (x)
f (a) f (b)
0
a
f (b) f (a)
b a
точке c є (a,b).
хотя бы в одной внутренней
c
f (c)
хотя бы в одной внутренней
f (c) 0
Геометрический смысл.
y
y
0
Пусть функция
Теорема Лагранжа.
c1
b x

13. Исследование функций

Теорема Ролля.
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Геометрический смысл.
Пусть функция
Теорема Лагранжа.
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
f (a) f (b)
Тогда :
f (c)
f (b) f (a)
b a
хотя бы в одной внутренней
f (c) 0
точке c є (a,b).
хотя бы в одной внутренней
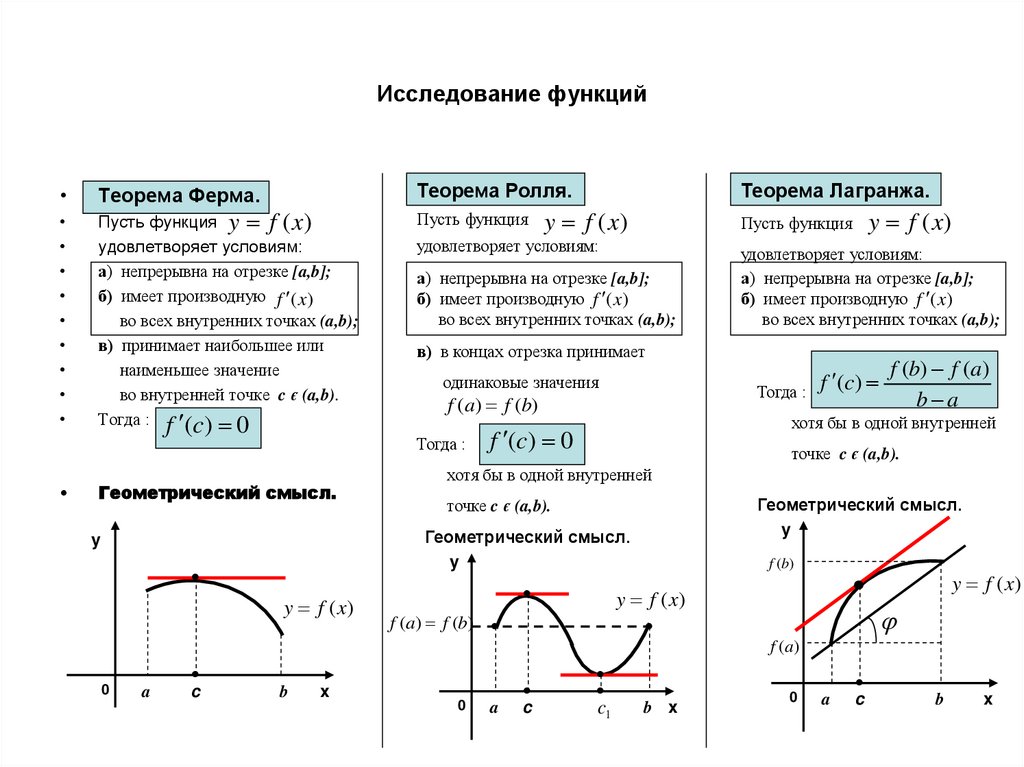
Геометрический смысл.
y
точке c є (a,b).
Геометрический смысл.
y
y
y f (x)
Пусть функция
f (b)
y f (x)
f (a) f (b)
y f (x)
f (a)
0
a
c
b
x
0
a
c
c1
b x
0
a
c
b
x

14. Доказательство теоремы Ферма

Пусть f ( x0 ) M наибольшее значение, т.е. f ( x ) M
для всех x [a; b]
y
По условию существует f ' ( x0 ) lim
.
x 0 x
Если существует такой предел, существуют и равны
y
y
lim
x 0 x
x 0 x
lim

15. Рассмотрим два случая:

1случай x 0
2 случай x 0
В обоих случаях:
y f ( x0 x) f ( x0 ) 0
В первом случае
y
0, так как y 0, x 0
x
Во втором случае
y
0, так как y 0, x 0
x

16. Пусть

x 0
y
Тогда в первом случае lim
0
x 0 x
y
0
Во втором случае lim
x 0 x
y
f ' ( x0 ) 0
x 0 x
0 lim
f ' ( x0 ) 0

17. Доказательство теоремы Ролля

Так как функция f(x) непрерывна на [a;b], то она принимает
на этом отрезке свое наибольшее M и наименьшее m
значения.
Если M = m, то f(x) = m = const, и c (a; b) f ' (c) 0.
Пусть M m, M m. Оба эти значения функция f(x)
принимает, но так как, по условию, f(a) = f(b), то хоть одно
из них достигается в некоторой точке c между a и b.
По теореме Ферма: f ' (c) 0.

18. Доказательство теоремы Лагранжа

1. Уравнение хорды имеет вид
y f ( a) k ( x a) ,
Рассмотрим функцию
где k
f (b) f (a)
b a
F ( x) f ( x) y f ( x) f ( a ) k ( x a ) ,
которая удовлетворяет теореме Ролля:
а) непрерывна на [a,b],
б) F ( x) x (a, b) ; F ( x) f ( x) k ;
в) F (a) F (b) 0 .
c (a, b) : F (c) 0 ,
т о ест ь f (c) k
f (b) f ( a )
b a

19. Формула Лагранжа

f (b) f (a) f (c)(b a), a c b

20. Исследование функций c помощью производной

y
–
–
–
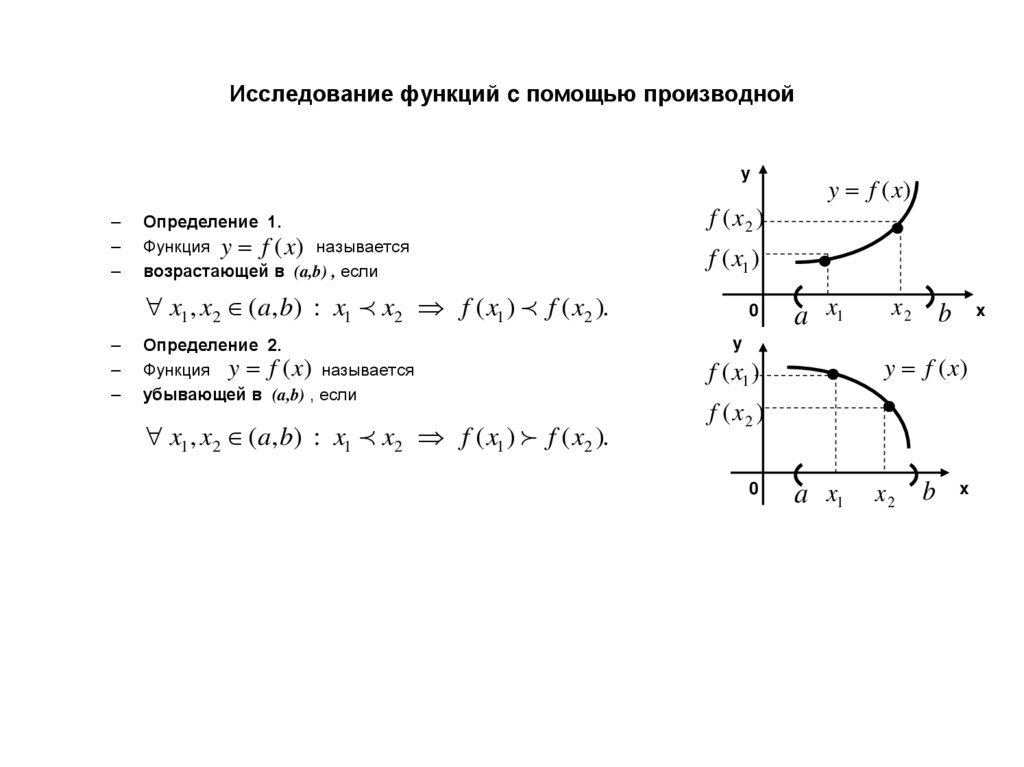
Определение 1.
Функция y f (x) называется
возрастающей в (a,b) , если
f ( x2 )
f ( x1 )
0
a x1
f ( x1 )
x1 , x2 (a, b) : x1 x2 f ( x1 ) f ( x2 ).
–
–
–
Определение 2.
Функция y f (x) называется
убывающей в (a,b) , если
x1 , x2 (a, b) : x1 x2 f ( x1 ) f ( x2 ).
y f (x)
y
f ( x2 )
0
a x1
x2
b
x
y f (x)
x2
b
x

21. Достаточный признак возрастания (убывания) функции на интервале

Теорема. Пусть функция f(x) непрерывна на [a;b] и
Пусть f ( x)
Тогда:
x (a, b) .
1) f ( x) 0 f ( x) возраст аетв (a, b) ;
2) f ( x) 0 f ( x) убывает в (a, b) .
Доказательство.
1.
2.
3.
x1 , x2 (a, b) : x1 x2
f ( x2 ) f ( x1 ) f (c)( x2 x1 ) ; c ( x1 , x2 ) (a, b).
f ( x) 0 x (a, b) f (c) 0
f ( x2 ) f ( x1 ) 0 f ( x2 ) f ( x1 ) ( убывает) .
f ( x) 0 x (a, b) f (c) 0
f ( x2 ) f ( x1 ) 0 f ( x2 ) f ( x1 ) (возрастает) .

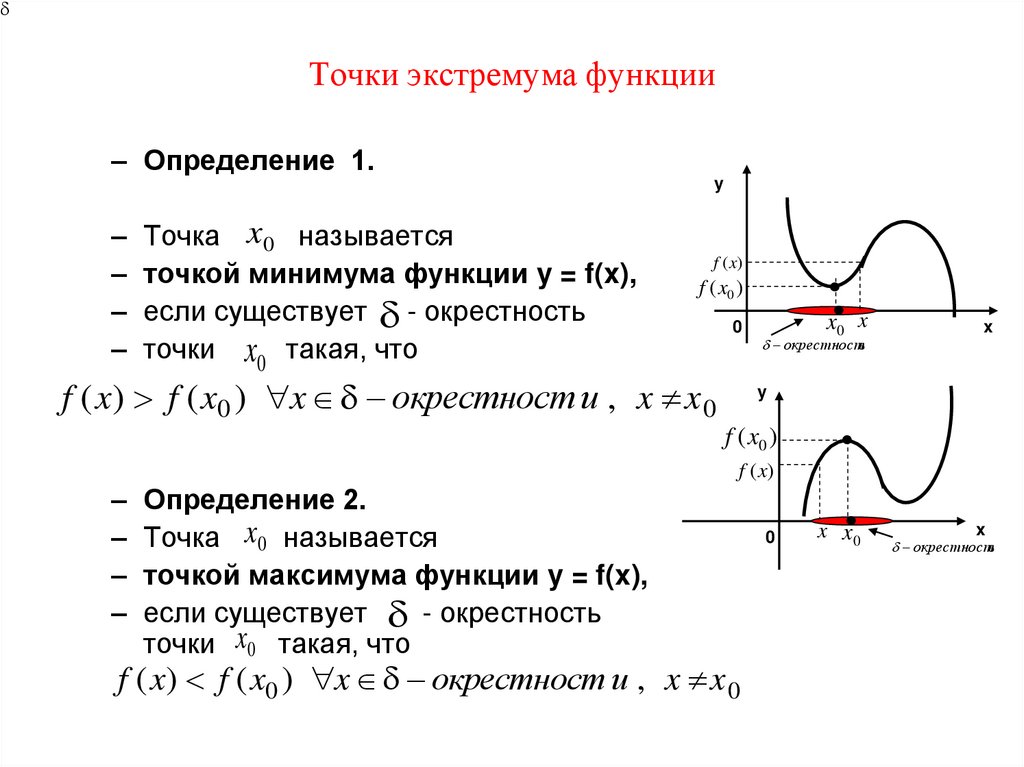
22. Точки экстремума функции

– Определение 1.
y
– Точка x0 называется
– точкой минимума функции y = f(x),
– если существует - окрестность
– точки x0 такая, что
f (x)
x x
f ( x0 )
0
f ( x) f ( x0 ) x окрестност и , x x 0
0
окрестность
x
y
f ( x0 )
f (x)
– Определение 2.
– Точка x0 называется
– точкой максимума функции y = f(x),
– если существует - окрестность
точки x0 такая, что
f ( x) f ( x0 ) x окрестност и , x x 0
0
x x 0
x
окрестность

23. Определение 3.

Точками экстремума называются
– точки минимума и точки максимума.
– Значения функции в этих точках
называют экстремальными значениями.

24. Необходимый признак экстремума

Если дифференцируемая функция y=f(x) имеет в точке x0
максимум или минимум, то ее производная равна нулю в этой
точке: f ( x ) 0.
0
Доказательство.
Пусть точка x0 - точка максимума, тогда значение функции в этой точке
является наибольшим значением для некоторого промежутка,
содержащего точку x0 : [ x0 x; x0 x] .
Тогда по теореме Ферма f ( x0 ) 0 .
Геометрически: если в точке максимума функция имеет производную, то
касательная к графику этой функции в данной точке будет параллельна
оси Ox.

25. Обратное неверно. Не во всякой точке, где производная равна нулю, есть min или max.

• Пример.
y x 3 ; y ' 3x 2 0; x 0.

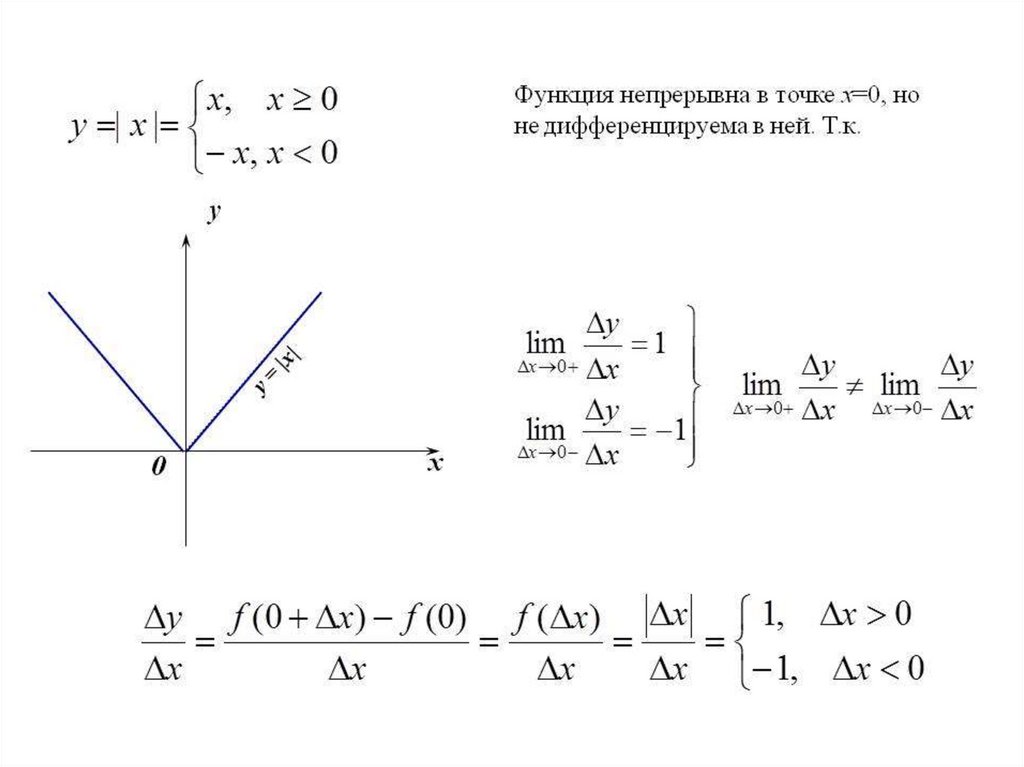
26. В точках, где производная не существует, тоже может быть max или min, или ни того ни другого.

• y = |x| , при x = 0 производной нет, но есть
min.

27.

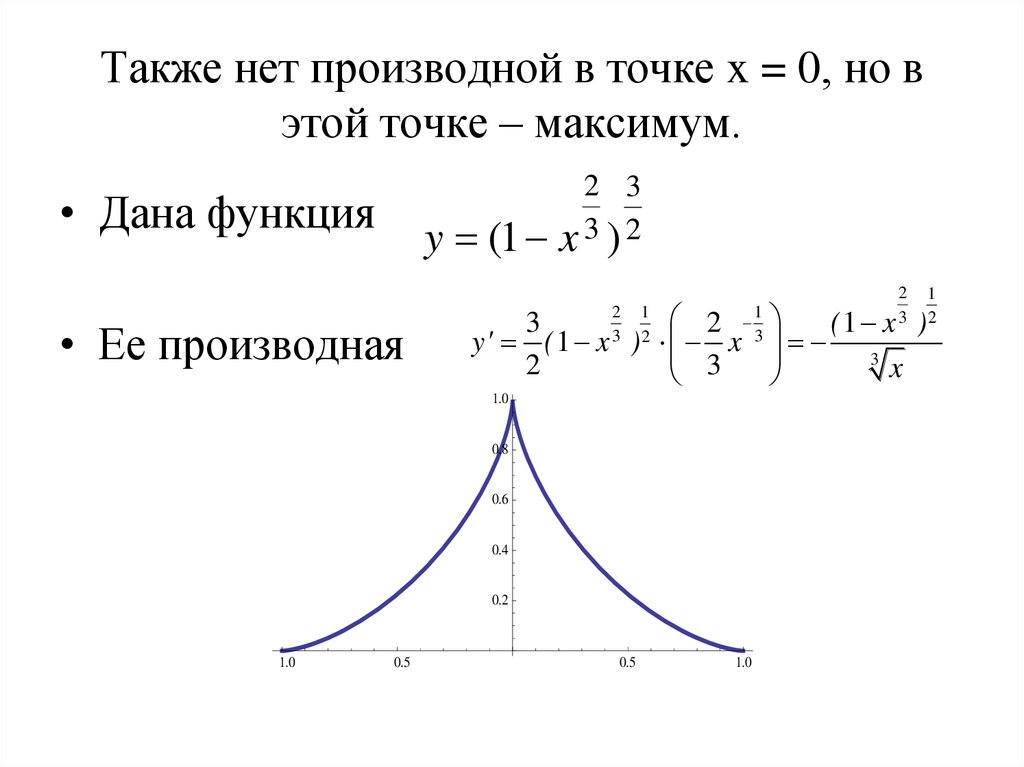
28. Также нет производной в точке x = 0, но в этой точке – максимум.

2 3
y (1 x 3 ) 2
• Дана функция
• Ее производная
1
2
1
3
1.0
0.8
0.6
0.4
0.2
1.0
0.5
2
3
2
3
(1 x )
y' ( 1 x ) x 3
2
x
3
2
3
0.5
1.0
1
2

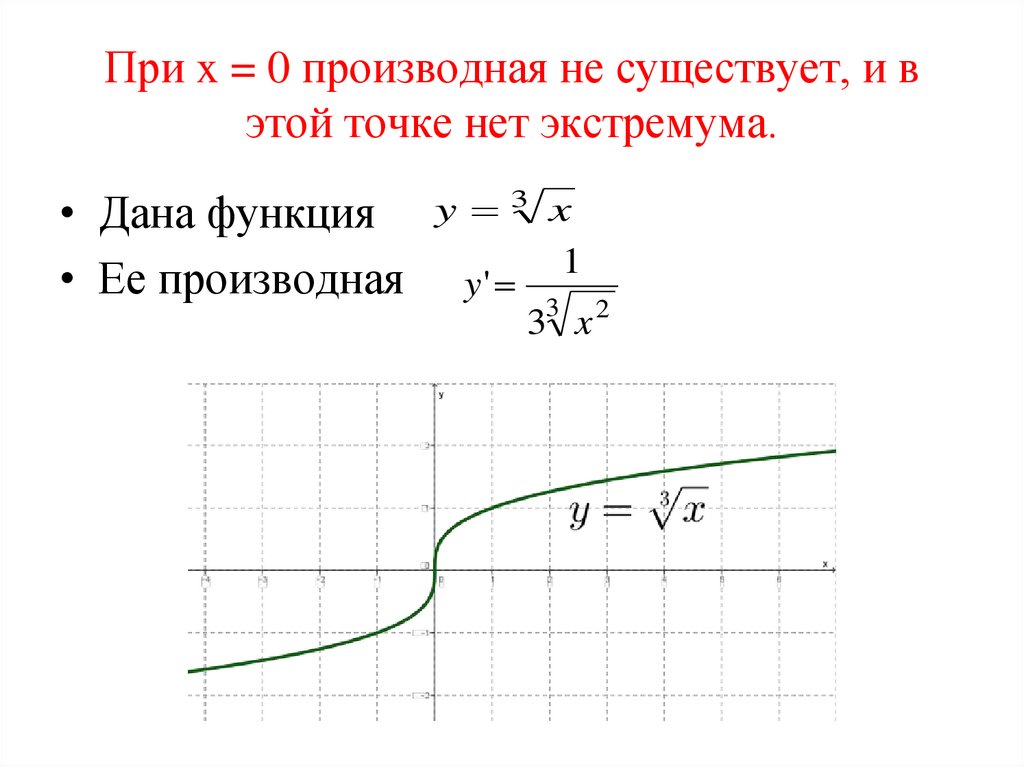
29. При x = 0 производная не существует, и в этой точке нет экстремума.

• Дана функция
• Ее производная
y 3 x
y'
1
33 x 2

30. Первый достаточный признак экстремума

Пусть функция y = f (x) определена в некотором
интервале, содержащем точку x0 , и имеет
производную во всех точках этого интервала
(кроме, может, самой точки x0 ). Если при переходе
через эту точку слева направо, производная меняет
знак с + на - , то x0 - точка максимума, если с – на
+, то x0 - точка минимума.

31. Доказательство

Пусть производная меняет знак с + на -, т.е. для всех x,
достаточно близких к x0 , будет:
f ' ( x) 0 при x x 0
f ' ( x) 0 при x x 0
f (x)
----------------------
x0

32. Применим формулу Лагранжа к разности

f ( x ) f ( x0 )
Получим
f ( x) f ( x0 ) f (c)( x x0 )
где с лежит между x и x0
1) x x0 , тогда c x0 , f (c) 0, f (c)( x x0 ) 0
f ( x ) f ( x0 ) 0 и f ( x ) f ( x0 )
2) x x0 , тогда c x0 , f (c) 0,
f ( x ) f ( x0 ) 0 и
f (c)( x x0 ) 0
f ( x ) f ( x0 )

33. Т.е. для всех значений x, достаточно близких к , значения функции меньше, чем значение функции в точке , следовательно, в точке

Т.е. для всех значений x, достаточно близких к x0 , значения
функции меньше, чем значение функции в точке x0 ,
следовательно, в точке x0 функция имеет максимум.

34.

Второй достаточный признак экстремума.
–
Теорема.
–
1.
y f ( x) определена
в окрест ности т очки x0
(включая т очку x0 ) ;
f ( x0 ) 0 ;
–
2.
–
3. f ( x ) 0
–
4.
0
f ( x0 ) 0
Точка x0 - точка минимума
Точка
x0 - точка максимума

35. Исследование функций

–
–
–
–
–
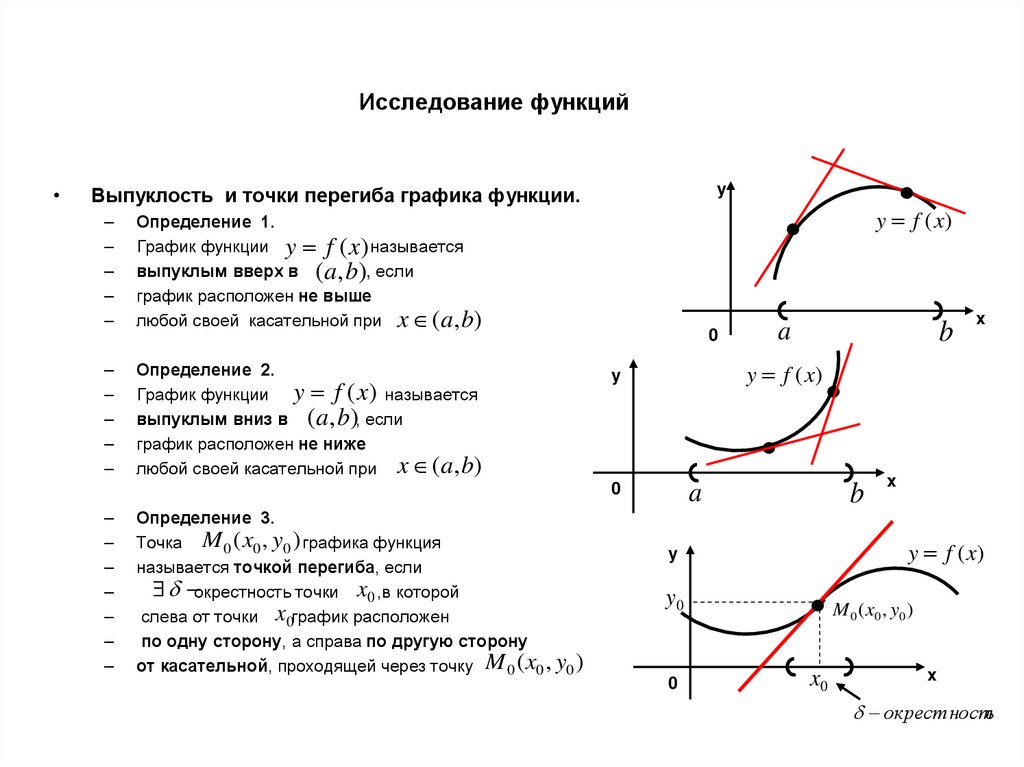
Определение 1.
График функции y f (x) называется
выпуклым вверх в ( a, b), если
график расположен не выше
любой своей касательной при x (a, b)
–
–
–
–
–
Определение 2.
График функции y f (x) называется
выпуклым вниз в ( a, b), если
график расположен не ниже
любой своей касательной при x (a, b)
0
Определение 3.
Точка M 0 ( x0 , y0 ) графика функция
называется точкой перегиба, если
окрестность точки x0 ,в которой
слева от точки x0график расположен
по одну сторону, а справа по другую сторону
от касательной, проходящей через точку M 0 ( x0 , y0 )
y f (x)
a
b
y f (x)
y
x
0
–
–
–
–
–
–
–
y
Выпуклость и точки перегиба графика функции.
x
b
a
y f (x)
y
y0
M (x , y )
0
x0
0
0
0
x
окрестность

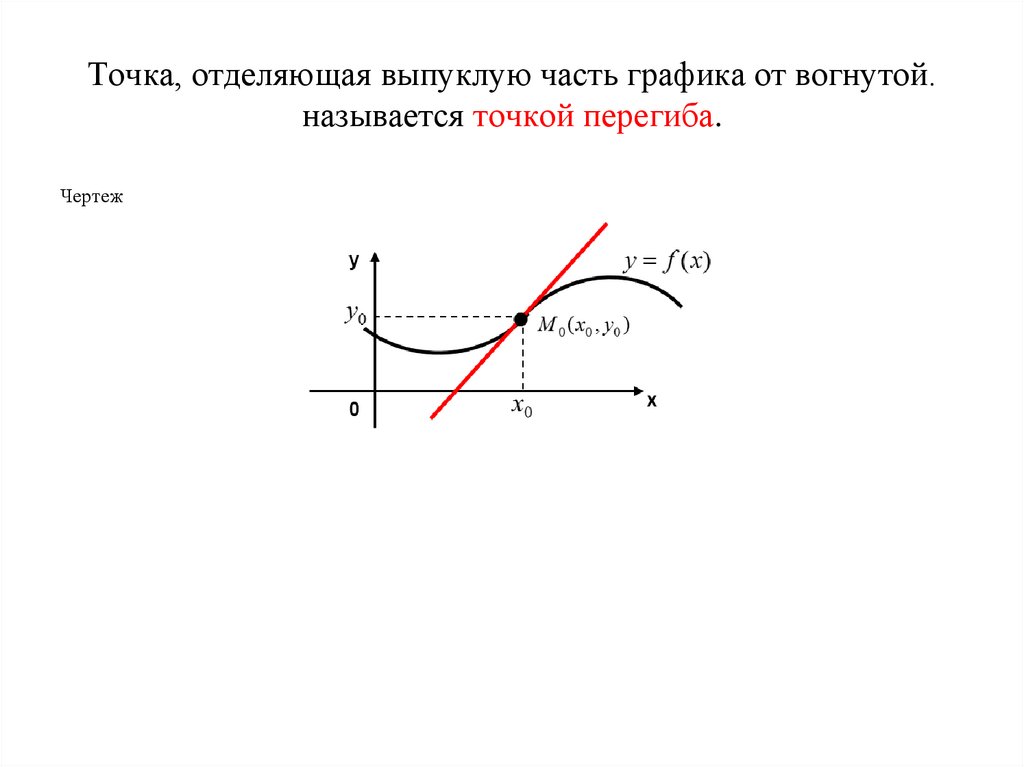
36. Точка, отделяющая выпуклую часть графика от вогнутой. называется точкой перегиба.

Чертеж

37. Исследование функций

Достаточный признак выпуклости.
–
Теорема.
–
1.
–
2.
–
3.
f ( x) x (a, b) ;
f ( x) 0
x ( a, b)
f ( x) 0
x ( a, b)
y f (x)
выпуклый вниз в ( a, b)
График функции
y f (x)
выпуклый вверх в ( a, b)
График функции

38. Дано: для всех . Доказать: график функции выпуклый вверх на этом интервале (выпуклый). Доказательство

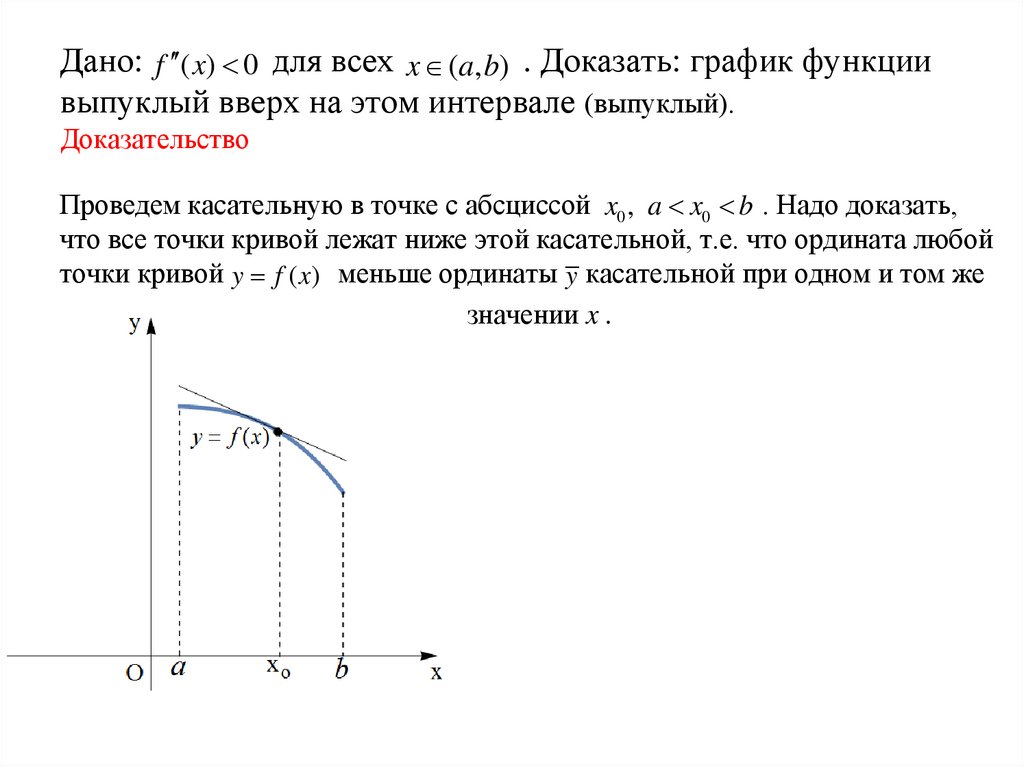
Дано: f ( x) 0 для всех x (a, b) . Доказать: график функции
выпуклый вверх на этом интервале (выпуклый).
Доказательство
Проведем касательную в точке с абсциссой x0 , a x0 b . Надо доказать,
что все точки кривой лежат ниже этой касательной, т.е. что ордината любой
точки кривой y f ( x) меньше ординаты y касательной при одном и том же
значении x .

39. - уравнение кривой,

y f ( x) - уравнение кривой,
y f ( x0 ) f ( x0 )( x x0 ) - уравнение касательной к кривой
в точке с абсциссой x0 .
Разность ординат при одном и том же значении x равна:
y y f ( x) f ( x0 ) f ( x0 )( x x0 )
По формуле Лагранжа f ( x) f ( x0 ) f (c)( x x0 ) , где c между x и x0 , тогда
y y f (c)( x x0 ) f ( x0 )( x x0 )
Еще раз применяем формулу Лагранжа
y y [ f (c) f ( x0 )]( x x0 ) , где c1 между
y y f (c1 )(c x0 )( x x0 )
и c.

40. Имеем два случая:

1. x x0 ,
x0 c x
x x0 0,
c x0 0, f (c1 ) 0
y y 0 y y
2. x x0 ,
x c x0
x x0 0, c x0 0, f (c1 ) 0
Таким образом, любая точка кривой лежит ниже касательной к кривой,
каковы бы ни были значения x и x0 на (a, b). Это значит, что кривая
выпукла вверх.
Что и требовалось доказать.

41. Исследование функций

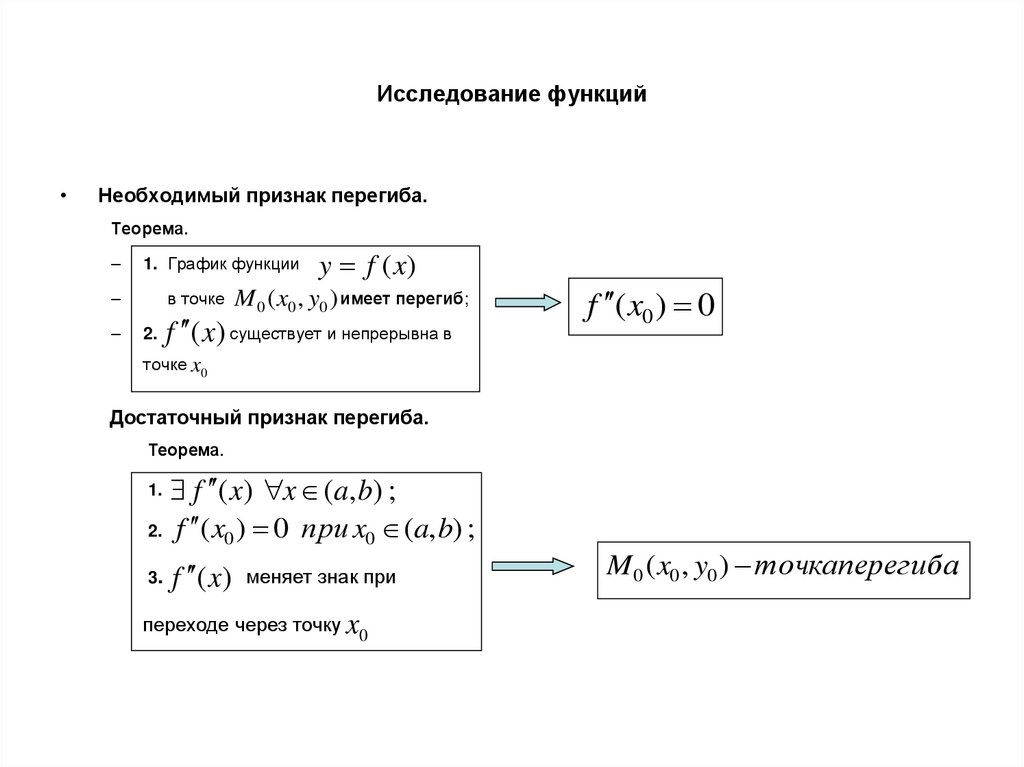
Необходимый признак перегиба.
Теорема.
–
1. График функции
–
–
y f (x)
в точке M 0 ( x0 , y0 ) имеет перегиб;
2.
f ( x) существует и непрерывна в
f ( x0 ) 0
точке x0
Достаточный признак перегиба.
Теорема.
f ( x) x (a, b) ;
2. f ( x0 ) 0 при x0 (a, b) ;
1.
3.
f ( x) меняет знак при
переходе через точку x0
M 0 ( x0 , y0 ) точка перегиба.

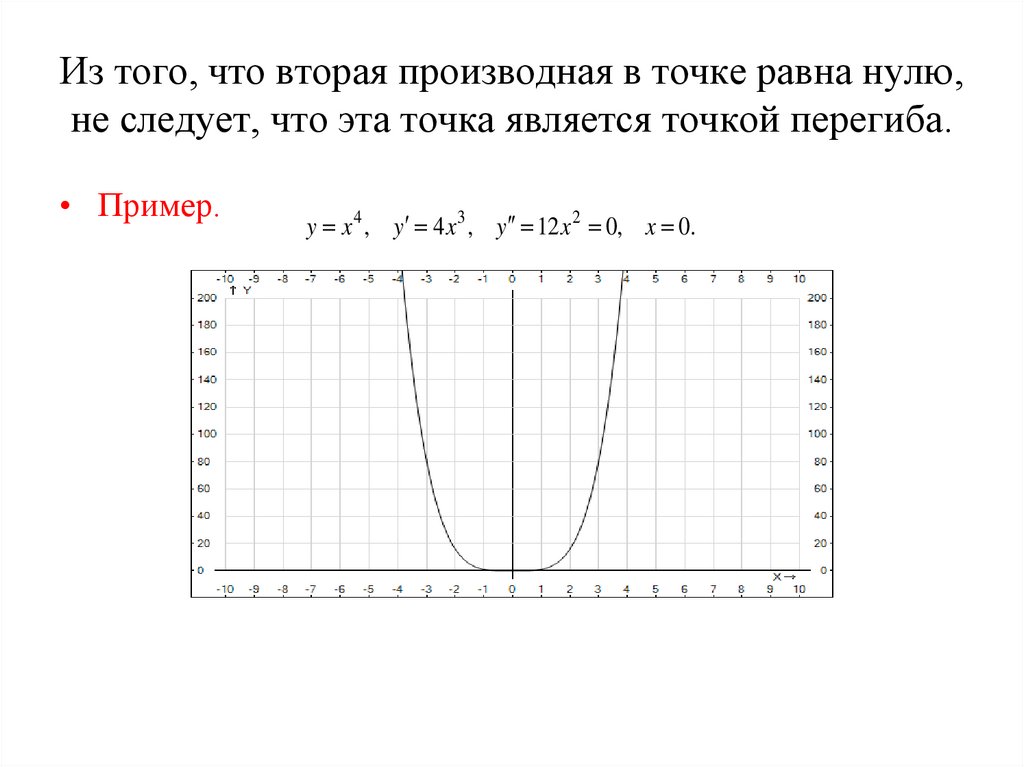
42. Из того, что вторая производная в точке равна нулю, не следует, что эта точка является точкой перегиба.

• Пример.
y x 4 , y 4 x 3 , y 12 x 2 0, x 0.

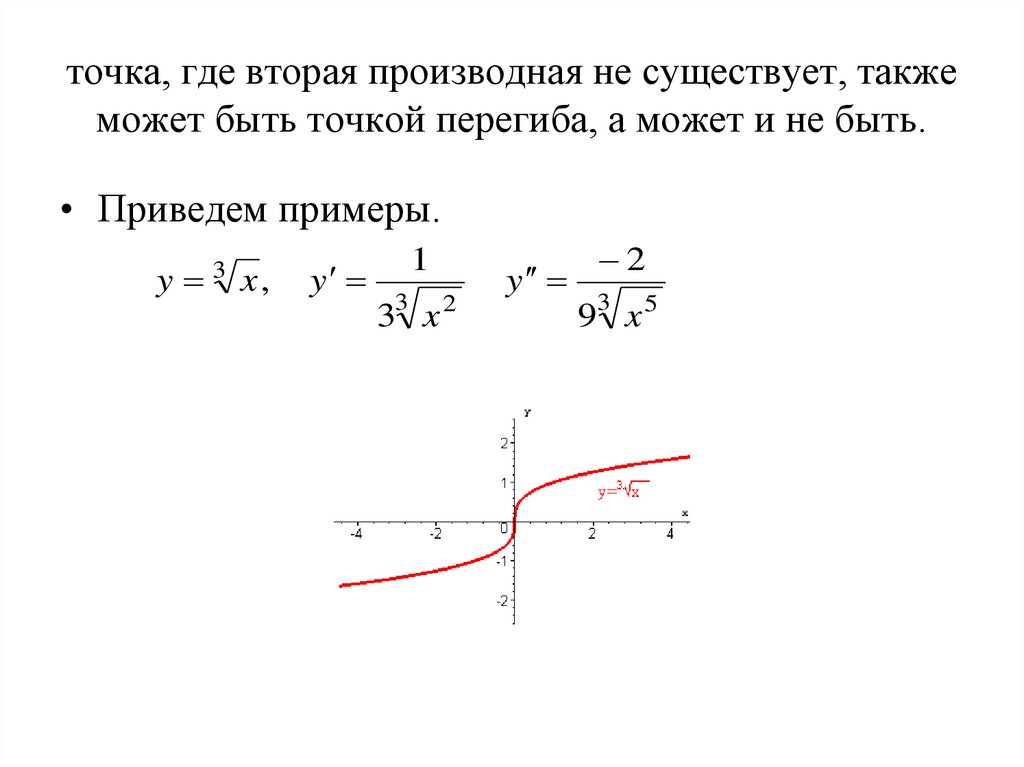
43. точка, где вторая производная не существует, также может быть точкой перегиба, а может и не быть.

• Приведем примеры.
y
3
x,
y
1
33 x 2
y
2
93 x 5

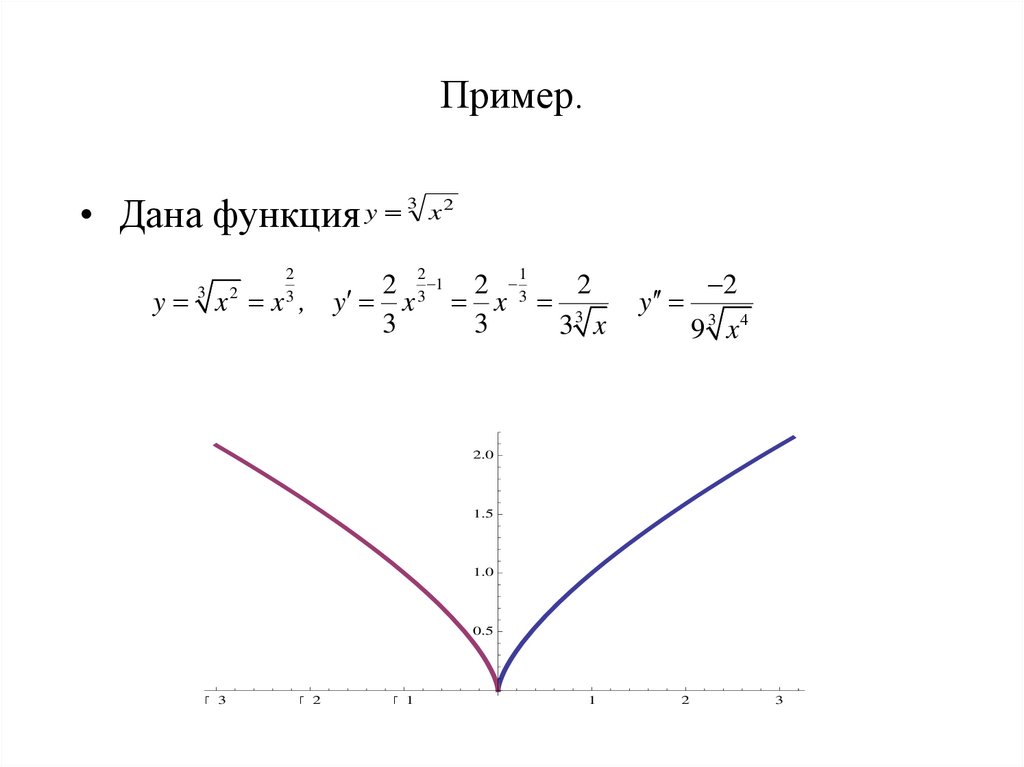
44. Пример.

• Дана функция
y 3 x2
2 23 1 2 13
2
y x x , y x x 3
3
3
3 x
3
2
2
3
y
2
9 3 x4
2.0
1.5
1.0
0.5
3
2
1
1
2
3

45.

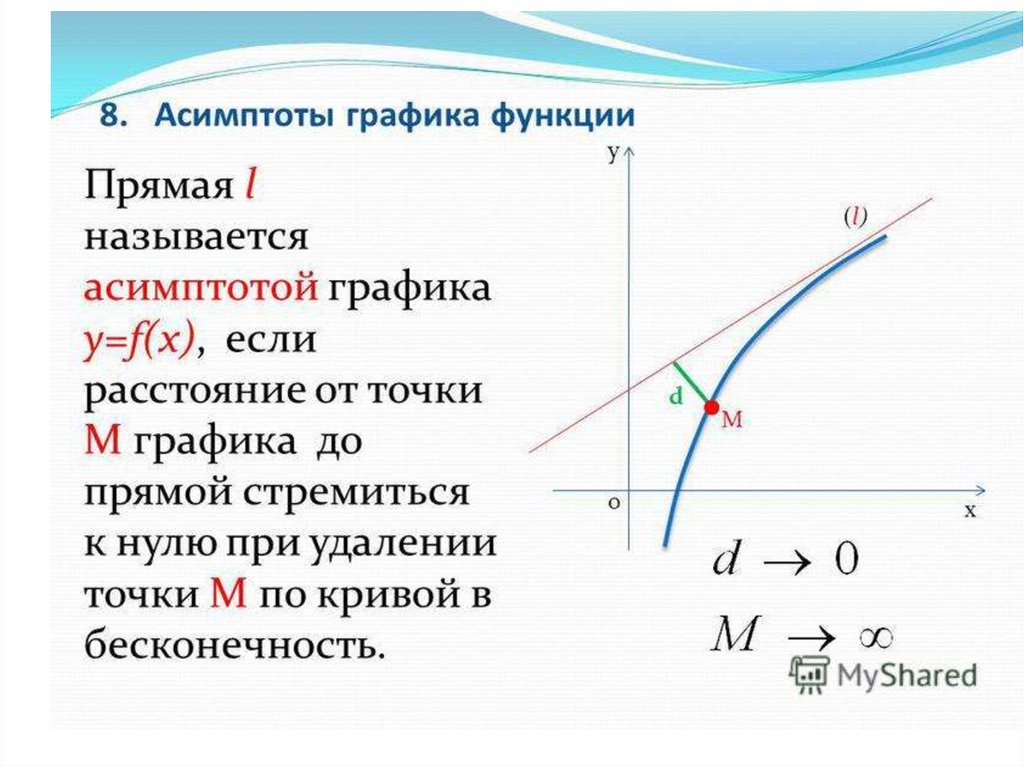
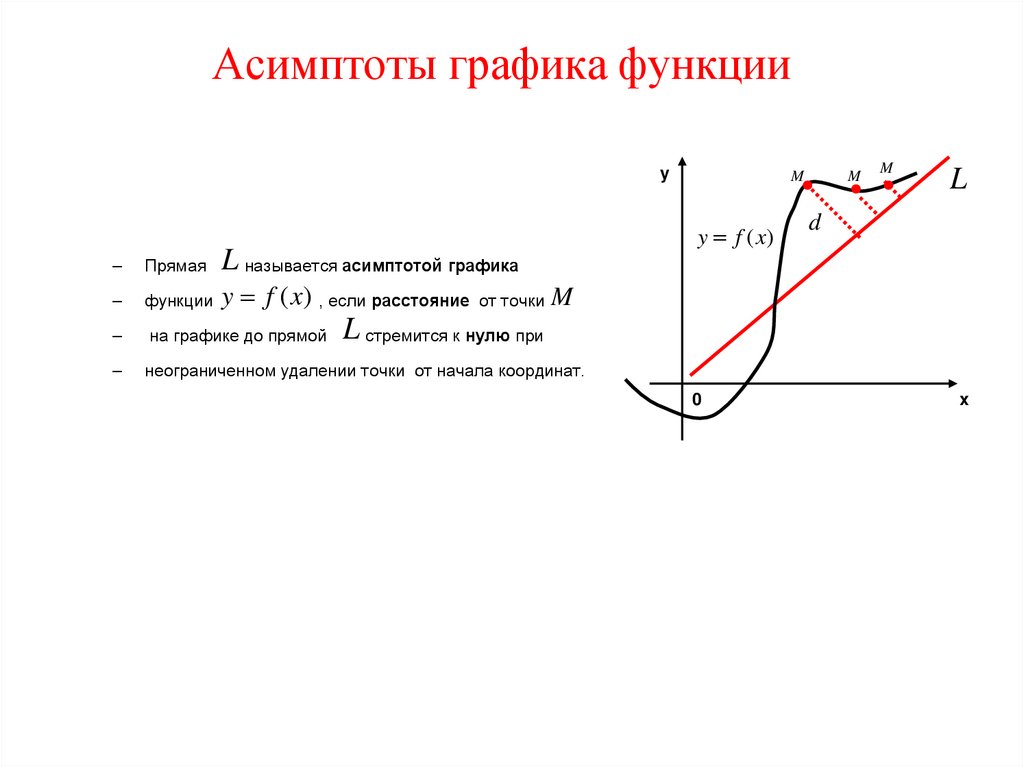
46. Асимптоты графика функции

y
L называется асимптотой графика
–
Прямая
–
функции y f (x) , если расстояние от точки M
–
на графике до прямой
–
неограниченном удалении точки от начала координат.
M
y f (x)
M
M
L
d
L стремится к нулю при
0
x

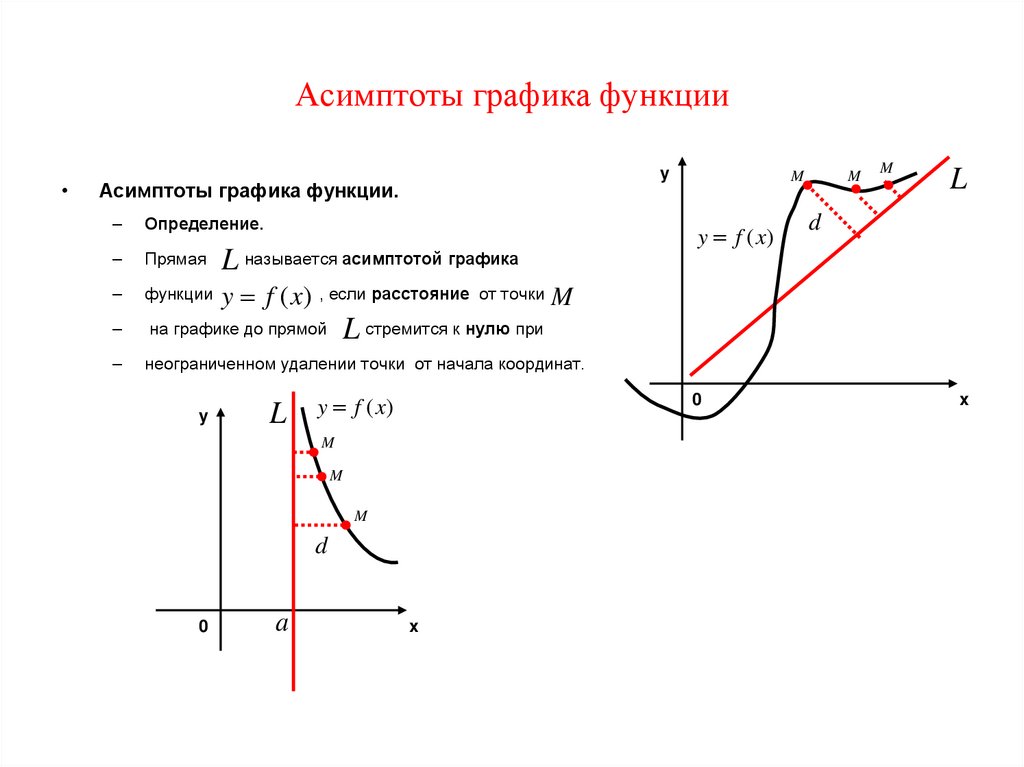
47. Асимптоты графика функции

y
Асимптоты графика функции.
–
Определение.
–
Прямая
–
функции y f (x) , если расстояние от точки M
–
на графике до прямой
–
неограниченном удалении точки от начала координат.
y
L называется асимптотой графика
L
y f (x)
0
M
M
d
a
y f (x)
M
M
L
d
L стремится к нулю при
M
0
M
x
x

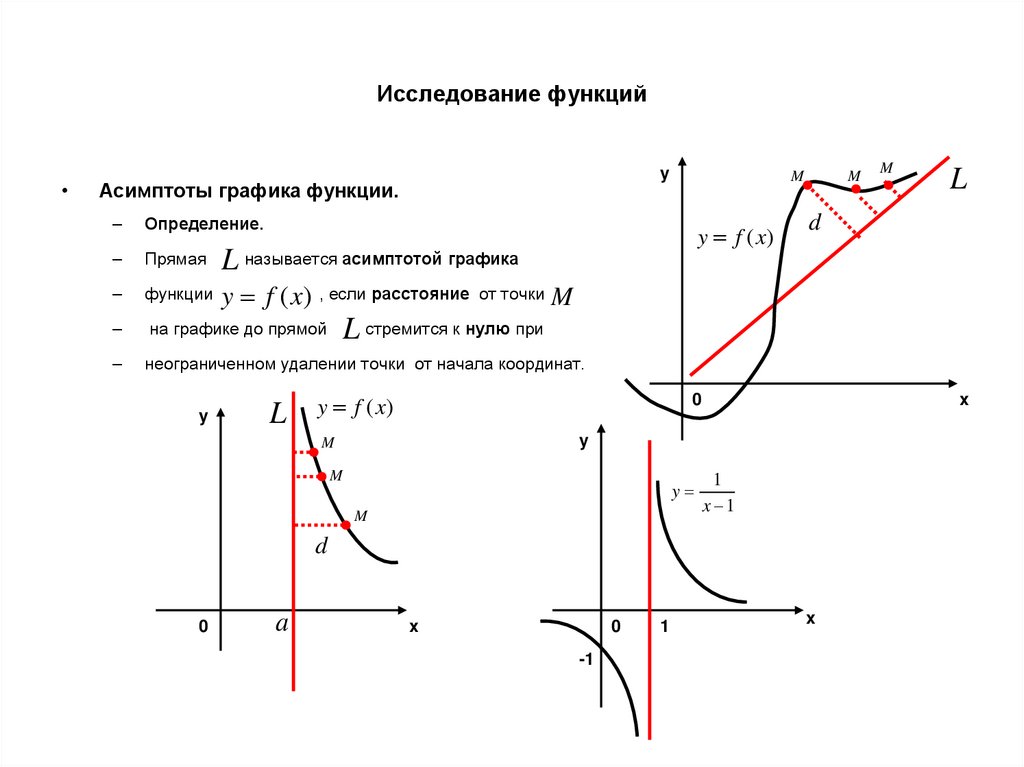
48. Исследование функций

y
Асимптоты графика функции.
–
Определение.
–
Прямая
–
функции y f (x) , если расстояние от точки M
–
на графике до прямой
–
неограниченном удалении точки от начала координат.
y
M
y f (x)
L называется асимптотой графика
L
M
y f (x)
d
0
x
y
M
y
M
1
x 1
d
a
L
L стремится к нулю при
M
0
M
x
0
-1
1
x

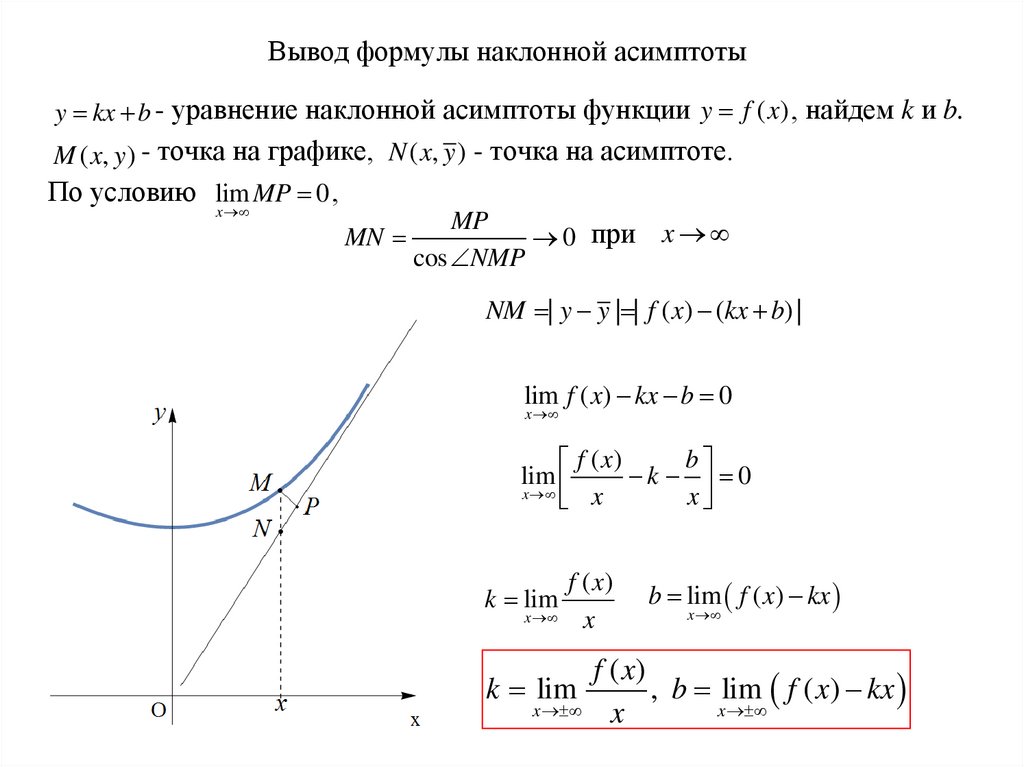
49. Вывод формулы наклонной асимптоты

y kx b - уравнение наклонной асимптоты функции y f ( x) , найдем k и b.
M ( x, y) - точка на графике, N ( x, y ) - точка на асимптоте.
По условию lim MP 0 ,
x
MP
MN
0 при x
cos NMP
NM | y y | | f ( x) (kx b) |
Разделим на x :
lim f ( x) kx b 0
x
b
f ( x)
lim
k 0
x
x
x
f ( x)
x
x
k lim
b lim f ( x) kx
x
f ( x)
, b lim f ( x) kx
x
x
x
k lim

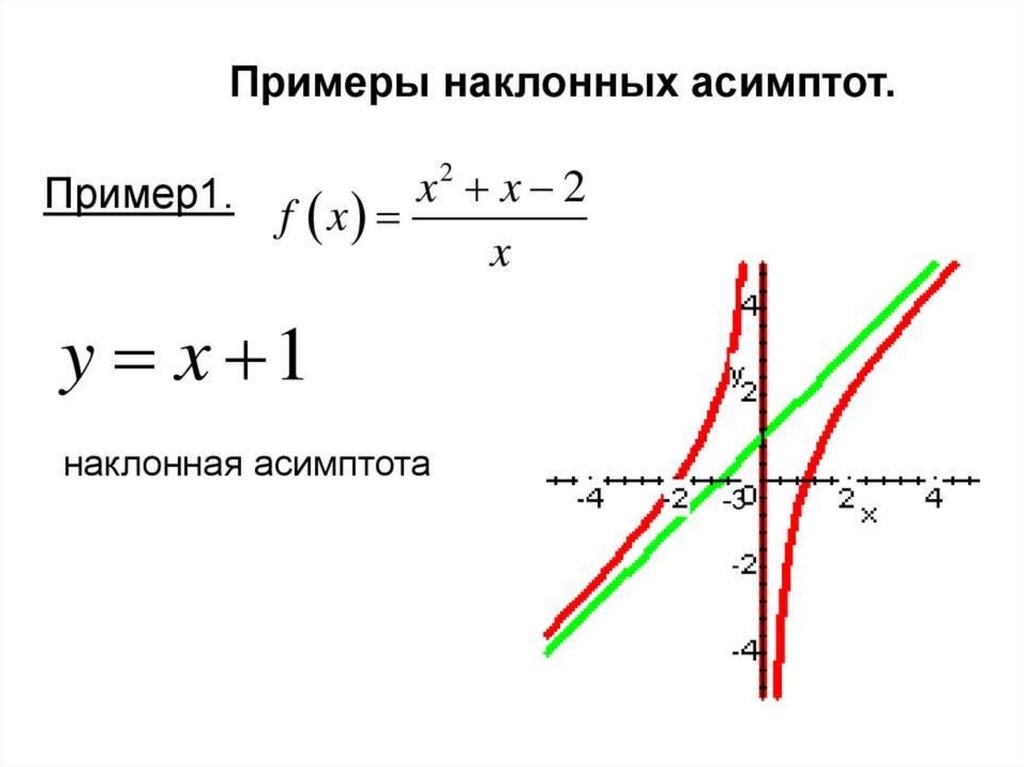
50. Пример

Найти асимптоты
1. Вертикальные
x2 x 2 ,
y
x
x 0 - точка разрыва
x 2 x 2 2
x 2 x 2 2
lim
, lim
x 0
x
0
x
0
x
0
- вертикальная асимптота.

51. 2. Наклонные

Ищем уравнение наклонной асимптоты в виде: y kx b
x2 x 2
1 2
1
2
2
2
2
f ( x)
x2 x 2
x
x lim
x x 1,
k lim
lim
lim x
2
2
x
x
x
x
x
x
x
1
x2
x2 x 2
x2 x 2 x2
x 2
b lim f ( x) kx lim
x lim
lim
x
x
x
x
x
x
x
x 2
2
1
x 1
lim x x lim
x
x
x
1
x
y x 1 - наклонная асимптота

52.

53. Асимптоты графика функции

Теорема 1.
–
–
x a
Прямая
является вертикальной асимптотой,
если хотя бы один из пределов
lim f ( x) или lim f ( x)
x a 0
–
x a 0
равен или
Теорема 2.
y kx b является наклонной асимптотой,
f ( x)
lim
k
x
x
Прямая
если
и
lim f ( x) kx b
x
Замечание. Горизонтальная асимптота - частный случай
наклонной асимптоты при k 0

54. Общая схема исследования функции

– 1. Область определения,
– 2. Четность, нечетность.
– 3. Периодичность.
– 4. Точки пересечения с осями координат.
– 5. Точки разрыва. Поведение функции в окрестности точек
разрыва.
– 6. Асимптоты графика.
– 7.Точки экстремума. Интервалы возрастания, убывания
функции.
- 8. Точки перегиба. Интервалы выпуклости, вогнутости.

55. Исследование функций

Пример 1.
y x 8x 16 x
3
–
Исследовать функцию и построить график
–
1. О.О.Ф.
–
2. Четность, нечетность:
2
x R
y( x) ( x) 8( x) 16( x) x 8x 16x ( x 8x 16x)
y ( x) y ( x) ; y ( x) y ( x) Функция общего вида
3
2
3
–
3. Непериодическая.
–
4. Точки пересечения с осями координат:
с Оу:
x 0 y 0 M 0 (0,0)
С Ох:
y 0 x 8 x 16 x 0
3
2
3
2
2
x( x 8 x 16) 0
2
x( x 4) 0
2
x0 0, x1 4
M 0 (0,0), M 1 (4,0)

56.

–
5. Асимптоты.
а) вертикальных асимптот нет;
б) наклонные:
y kx b
f ( x)
x 8x 16 x
2
k lim
lim
lim ( x 8x 16)
x
x
x
x
x
3
2
Наклонных асимптот нет
–
x
3
2
lim ( x 8 x 16 x)
6. Поведение при
x
lim ( x 8 x 16 x)
3
x
2

57. Исследование функций

Исследование с помощью первой производной.
2
y 3 x 16 x 16
16 16 4 3 16 16 8
2
y 0 3 x 16 x 16 0 x1, 2
6
6
4
x1 4, x2
3
+
+ max min
y
2
4
3
4
4 3
4 2
4 256
y ( ) ( ) 8 ( ) 16
9,5
3
3
3
3 27
y (4) 0
4
х

58. Исследование функций

Исследование с помощью второй производной.
y (3x 16 x 16) 6 x 16
2
y 0 6 x 16 0 x
y
-
16 8
6 3
+
8
3
х

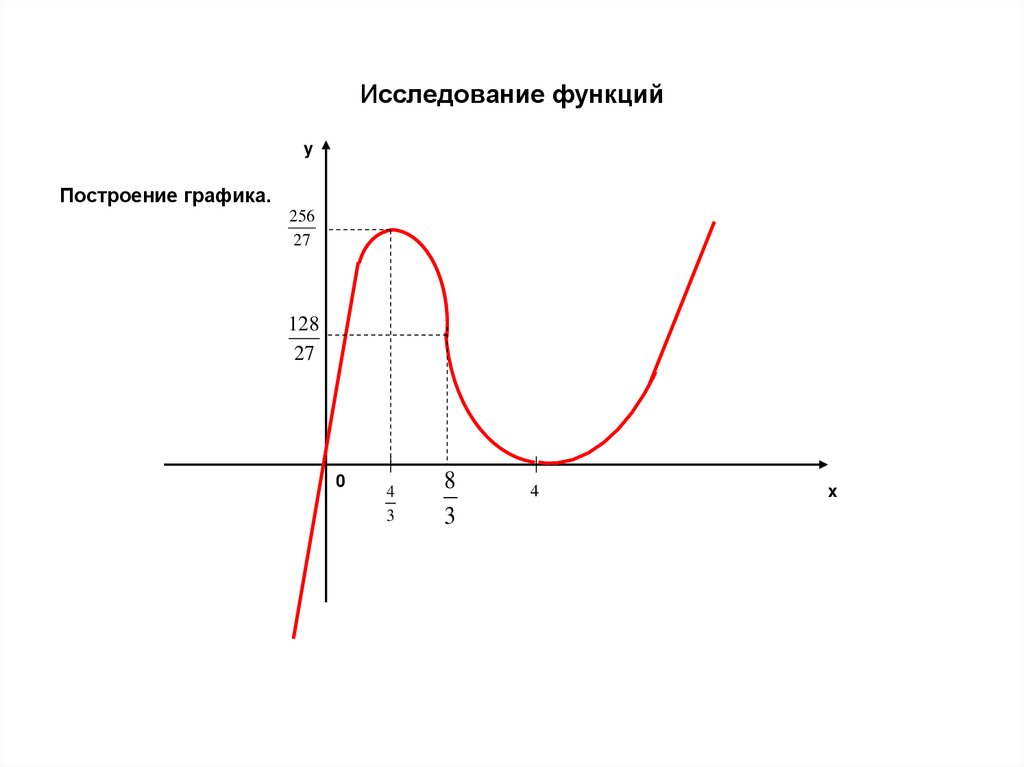
59. Исследование функций

y
Построение графика.
256
27
128
27
0
4
3
8
3
4
x

60. Исследование функций

Пример 2.
–
–
–
–
–
–
x2
Исследовать функцию и построить график y
1 x
.
2
1. О.О.Ф.: x 1 ;
x
x 1 o 1 x
x2
lim
x 1 o 1 x
lim
x 1 т очка разрыва
вт орогорода.
2. Четность, нечетность:
( x) 2
x2
y ( x)
1 ( x) 1 x
y( x) y( x) ; y( x) y( x)
3. Непериодическая.
4. Точки пересечения с осями координат: x 0 ;
5. Асимптоты:
• а) вертикальные: x 1 .
• б) наклонные: y kx b ;
Функция
общего
вида.
y 0.
f ( x)
x
lim
1 ;
x
x
x
1 x
x2
b lim f ( x) kx lim
x 1 .
x
x 1 x
k lim
y x 1

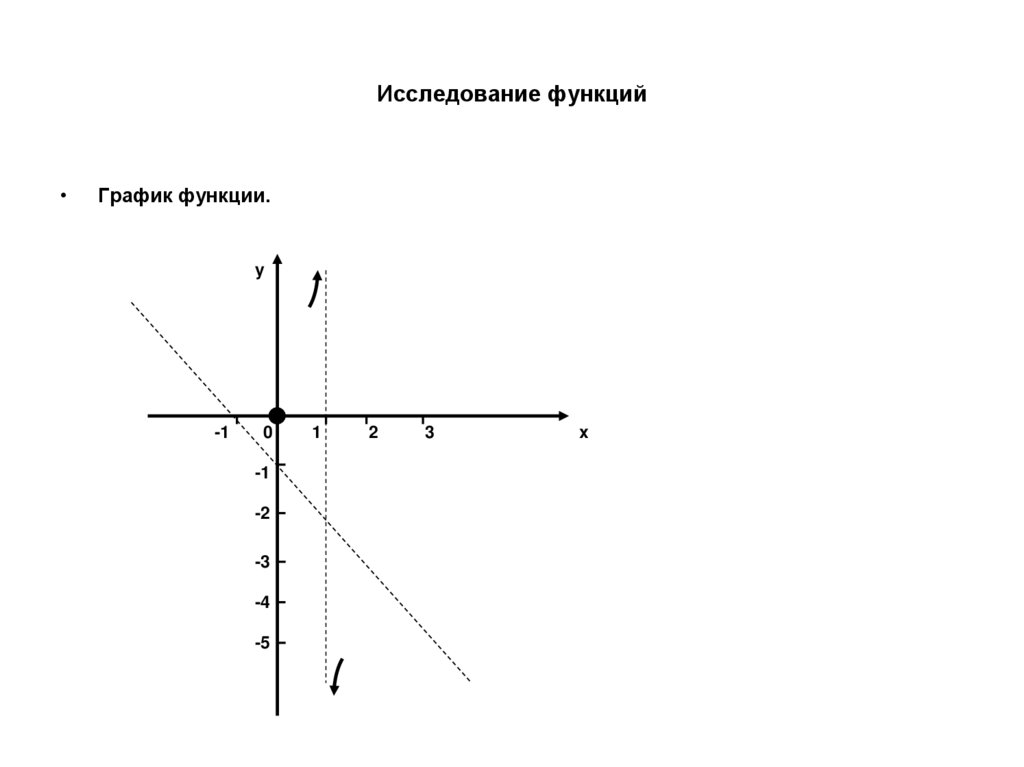
61. Исследование функций

График функции.
y
-1
0
-1
-2
-3
-4
-5
1
2
3
x

62. Исследование функций

Исследование с помощью первой производной.
2 x(1 x) x 2 ( 1) x(2 x)
y
;
(1 x) 2
(1 x) 2
y 0 x1 0 ; x2 2 ;
y1 0 ; y2 4 ;
y не существует: x 1
y
min
0
max
1
2
x

63. Точки перегиба. Интервалы выпуклости, вогнутости

Находим вторую производную
2 x x 2 (2 2 x)(1 x) 2 (2 x x 2 ) 2(1 x) ( 1)
y
2
4
(1 x)
(1 x)
2(1 x)[(1 x) 2 (2 x x 2 )] 2[1 2 x x 2 2 x x 2 ]
2
(1 x) 4
(1 x)3
(1 x)3
2
0 - точек перегиба нет
3
(1 x)

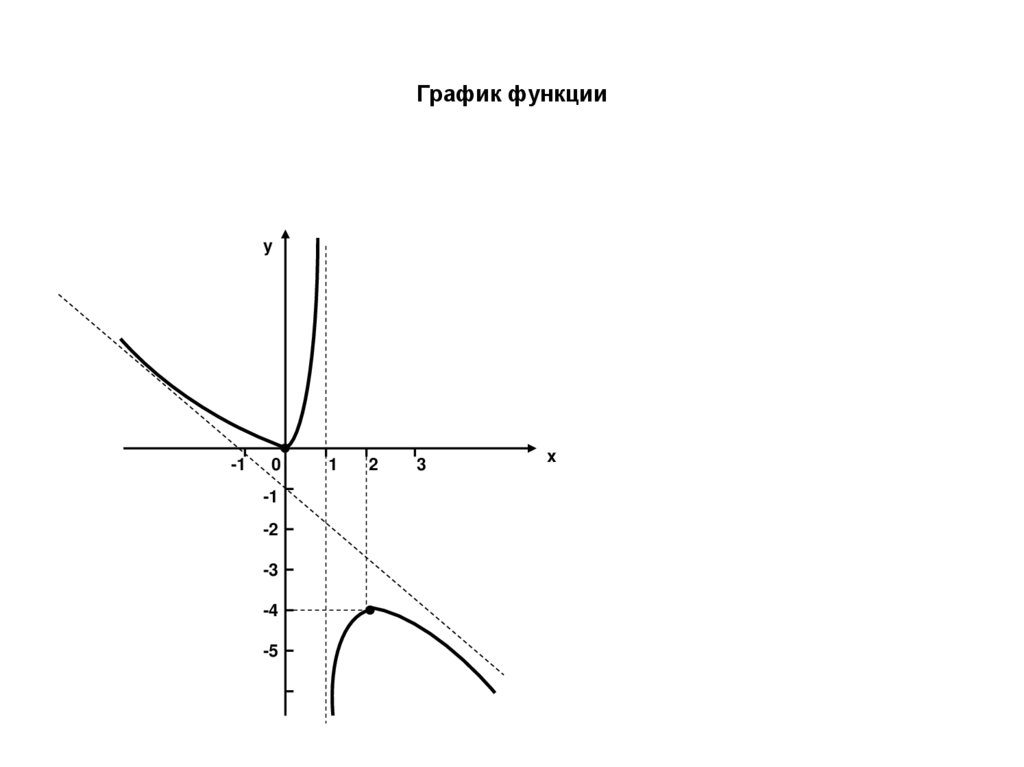
64. График функции

y
-1
0
-1
-2
-3
-4
-5
1
2
3
x