Лекция 1.Форма и размеры земли ЗВУК

1. Форма и размеры Земли

Подготовлено:
Гура Дмитрий
29.09.2016

2. Фигура Земли

Фигура Земли обусловлена воздействием
различных процессов, решающими из
которых являются силы внутреннего
тяготения и центробежная.
Под действием этих сил Земля имеет форму
шара, сплюснутого у полюсов – форму
сфероида
Говорить о Земле только как о сфероиде
можно с большим обобщением, так как
реальная поверхность Земли – это
поверхность материков, дна морей и
океанов. Она сложна и напоминает сфероид
лишь в целом.
Учитывая, что введено понятие уровенной
поверхности , что обусловлено тем, что 3/4
площади земного шара занимают моря и
океаны для изучения фигуры Земли введены
понятия уровенной поверхности
(поверхностей различных морей и океанов) и
основной уровенной поверхности,
совпадающей со средней поверхностью
морей и океанов, находящихся в спокойном
состоянии.

3.

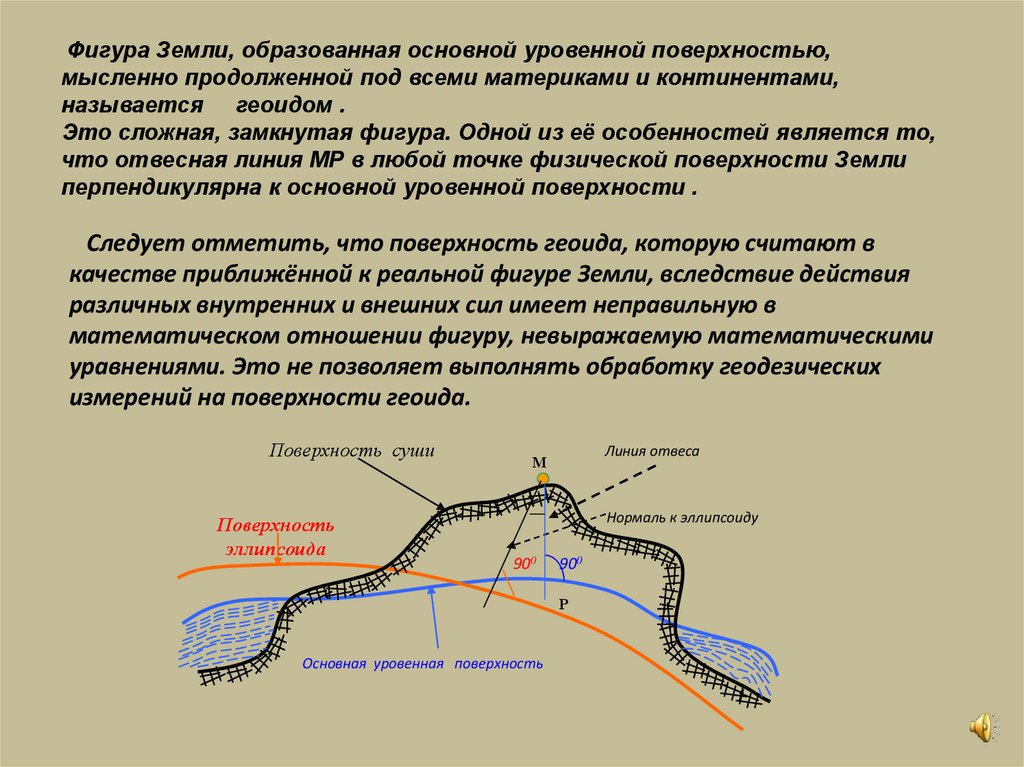
Фигура Земли, образованная основной уровенной поверхностью,
мысленно продолженной под всеми материками и континентами,
называется геоидом .
Это сложная, замкнутая фигура. Одной из её особенностей является то,
что отвесная линия МР в любой точке физической поверхности Земли
перпендикулярна к основной уровенной поверхности .
Следует отметить, что поверхность геоида, которую считают в
качестве приближённой к реальной фигуре Земли, вследствие действия
различных внутренних и внешних сил имеет неправильную в
математическом отношении фигуру, невыражаемую математическими
уравнениями. Это не позволяет выполнять обработку геодезических
измерений на поверхности геоида.
Поверхность суши
Поверхность
эллипсоида
Линия отвеса
М
Нормаль к эллипсоиду
900
900
Р
Основная уровенная поверхность

4.

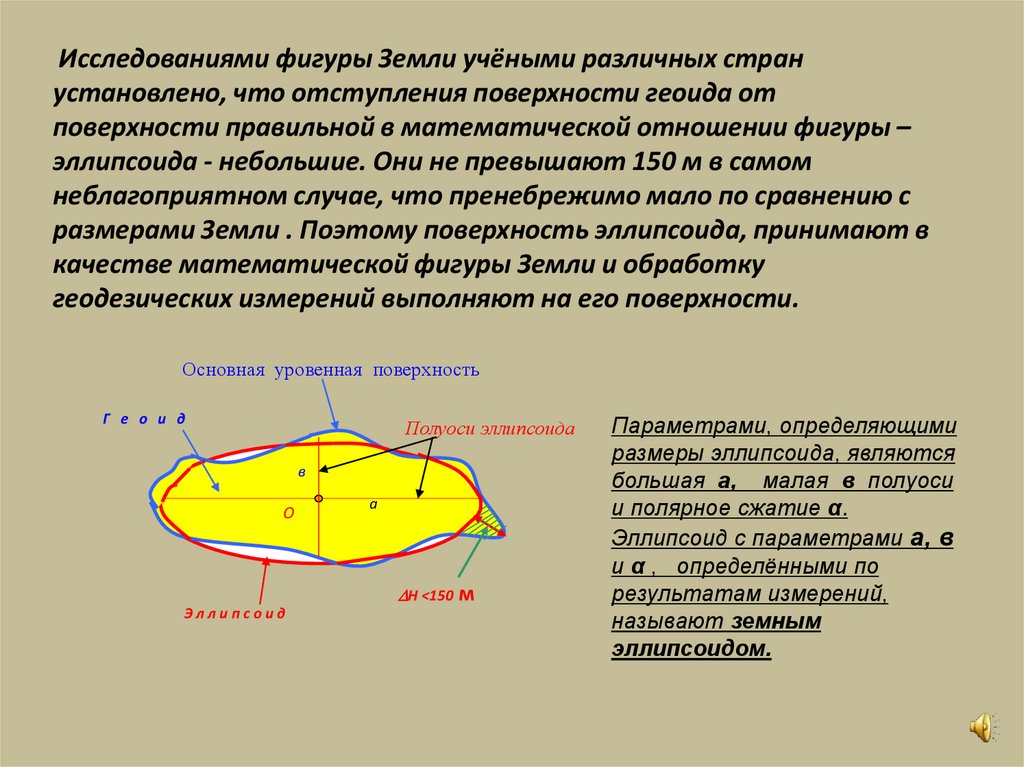
Исследованиями фигуры Земли учёными различных стран
установлено, что отступления поверхности геоида от
поверхности правильной в математической отношении фигуры –
эллипсоида - небольшие. Они не превышают 150 м в самом
неблагоприятном случае, что пренебрежимо мало по сравнению с
размерами Земли . Поэтому поверхность эллипсоида, принимают в
качестве математической фигуры Земли и обработку
геодезических измерений выполняют на его поверхности.
Основная уровенная поверхность
Г е о и д
Полуоси эллипсоида
в
О
а
H <150 м
Эллипсоид
Параметрами, определяющими
размеры эллипсоида, являются
большая а, малая в полуоси
и полярное сжатие α.
Эллипсоид с параметрами а, в
и α , определёнными по
результатам измерений,
называют земным
эллипсоидом.

5. Системы координат, применяемые в геодезии. Понятие о прямоугольной системе координат Гаусса-Крюгера.

Под координатами в общем смысле понимают числа, определяющие
положение точки на плоскости, любой поверхности или в пространстве.
В геодезии под координатами понимают совокупность трёх
чисел, определяющих положение точки земной поверхности
относительно некоторой исходной поверхности.
При определении координат точек земной поверхности
в геодезии
применяют следующие системы координат:
•систему геодезических координат;
•систему астрономических координат;
•систему прямоугольных координат;
•систему полярных координат.

6.

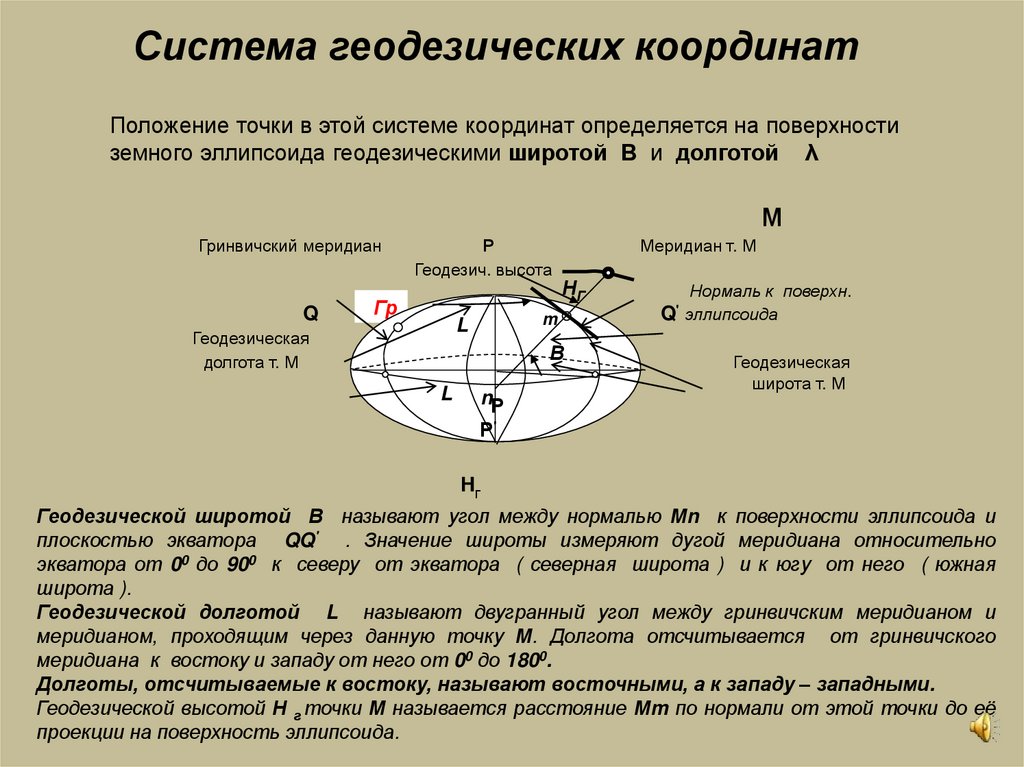
Система геодезических координат
Положение точки в этой системе координат определяется на поверхности
земного эллипсоида геодезическими широтой В и долготой λ
М
Гринвичский меридиан
Q
Геодезическая
долгота т. М
Р
Геодезич. высота
Гр
НГ
m
L
.
Меридиан т. М
В
L
nР
Р'
Нормаль к поверхн.
Q' эллипсоида
Геодезическая
широта т. М
Hг
Геодезической широтой В называют угол между нормалью Мn к поверхности эллипсоида и
плоскостью экватора QQ' . Значение широты измеряют дугой меридиана относительно
экватора от 00 до 900 к северу от экватора ( северная широта ) и к югу от него ( южная
широта ).
Геодезической долготой L называют двугранный угол между гринвичским меридианом и
меридианом, проходящим через данную точку М. Долгота отсчитывается от гринвичского
меридиана к востоку и западу от него от 00 до 1800.
Долготы, отсчитываемые к востоку, называют восточными, а к западу – западными.
Геодезической высотой Н г точки М называется расстояние Мm по нормали от этой точки до её
проекции на поверхность эллипсоида.

7. Система астрономических координат

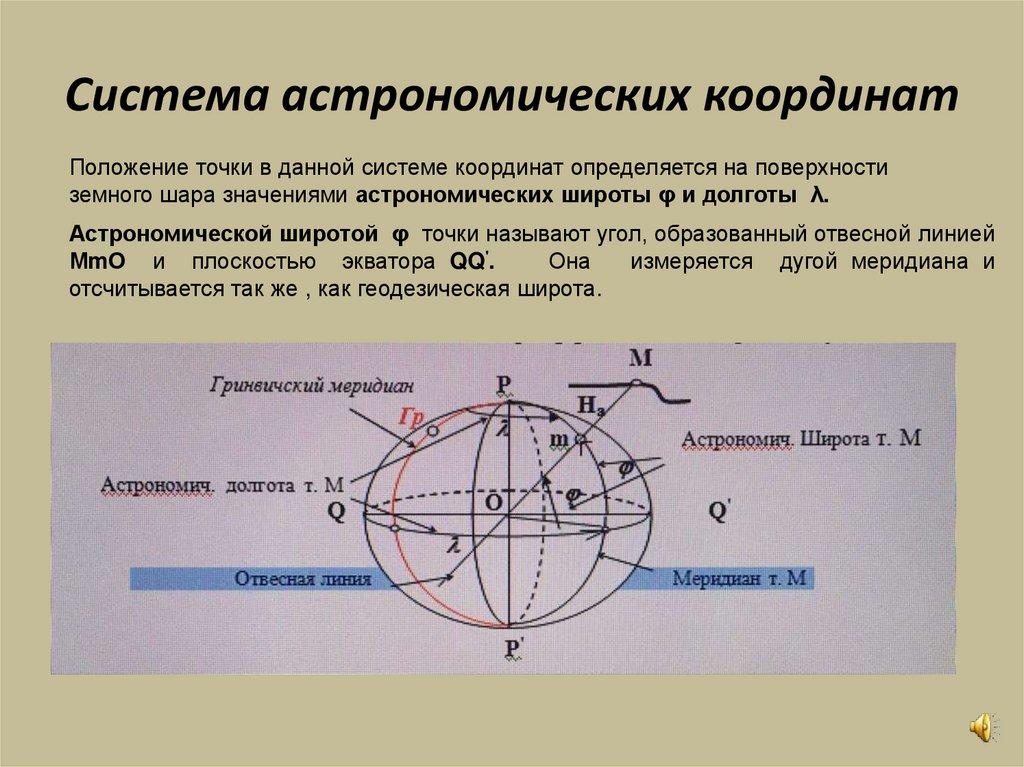
Положение точки в данной системе координат определяется на поверхности
земного шара значениями астрономических широты φ и долготы λ.
Астрономической широтой φ точки называют угол, образованный отвесной линией
МmО и плоскостью экватора QQ'.
Она
измеряется дугой меридиана и
отсчитывается так же , как геодезическая широта.

8.

Астрономической долготой λ называют двугранный угол, образованный
гринвичским меридианом и меридианом, проходящим через данную точку
М. Долгота измеряется дугой экватора и отсчитывается так
же, как и геодезическая долгота.
Ортометрической высотой На точки М называют расстояние по линии
отвеса Мm до поверхности геоида.
Как следует из определения понятий широт и долгот на поверхности
земного эллипсоида и геоида между ними существуют некоторые
различия, обусловленные тем, что линия отвеса и нормаль к поверхности
эллипсоида не совпадают между собой, а образуют некоторый угол u (
рис.1), называемый уклоненим отвестной линии от нормали к
поверхности эллипсоида.
При инженерно-геодезических работах, как правило, нет необходимости
учитывать уклонение отвесной линии и различать геодезические и
астрономические координаты, что обусловлено точностью этих работ.
Поэтому системы геодезических и географических координат объединяют
общим понятием – система географических координат, полагая что В =
φ , L = λ.

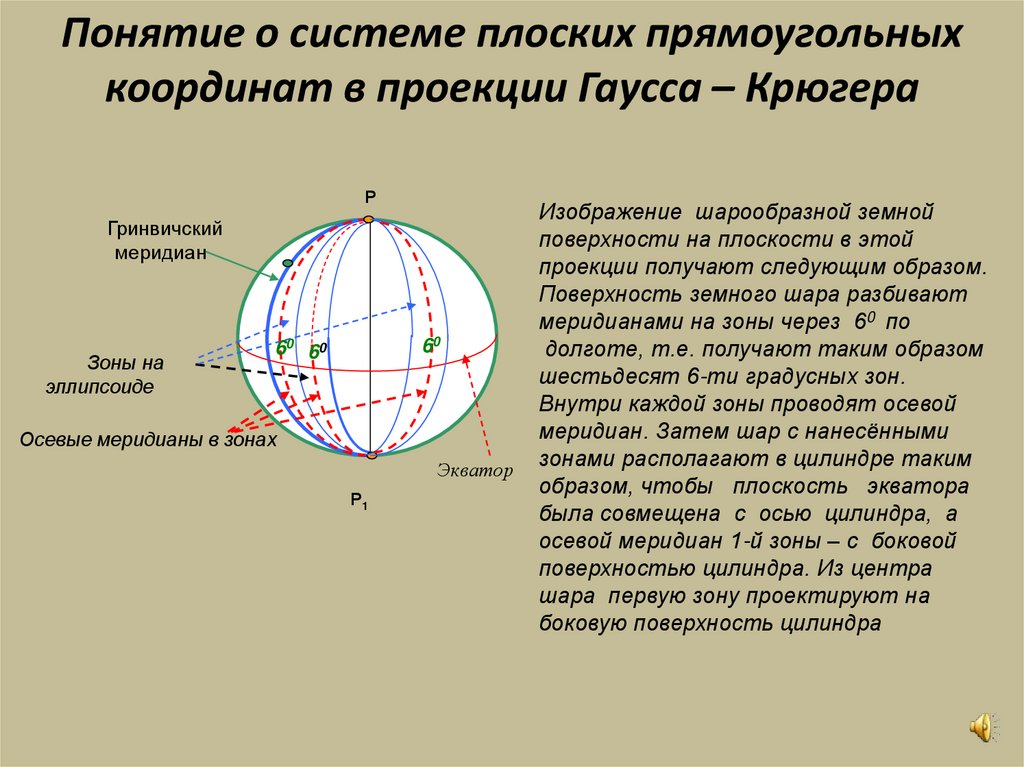
9. Понятие о системе плоских прямоугольных координат в проекции Гаусса – Крюгера

Р
Гринвичский
меридиан
Зоны на
эллипсоиде
60
60 60
Осевые меридианы в зонах
Экватор
Р1
Изображение шарообразной земной
поверхности на плоскости в этой
проекции получают следующим образом.
Поверхность земного шара разбивают
меридианами на зоны через 60 по
долготе, т.е. получают таким образом
шестьдесят 6-ти градусных зон.
Внутри каждой зоны проводят осевой
меридиан. Затем шар с нанесёнными
зонами располагают в цилиндре таким
образом, чтобы плоскость экватора
была совмещена с осью цилиндра, а
осевой меридиан 1-й зоны – с боковой
поверхностью цилиндра. Из центра
шара первую зону проектируют на
боковую поверхность цилиндра

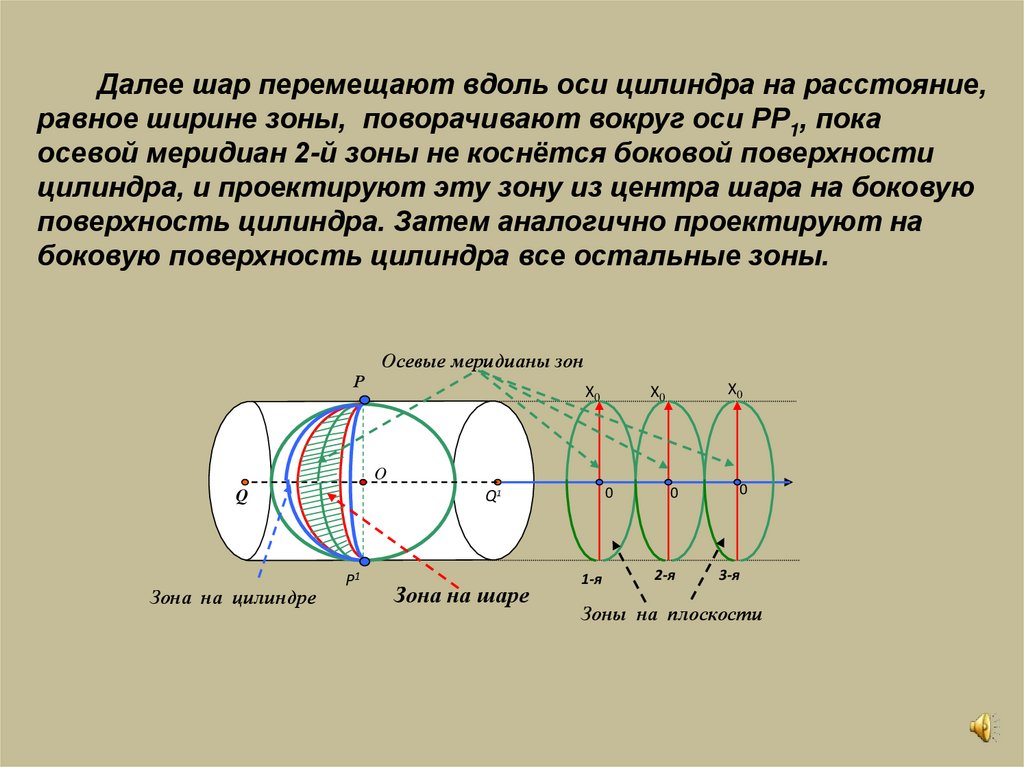
10.

Далее шар перемещают вдоль оси цилиндра на расстояние,
равное ширине зоны, поворачивают вокруг оси РР1, пока
осевой меридиан 2-й зоны не коснётся боковой поверхности
цилиндра, и проектируют эту зону из центра шара на боковую
поверхность цилиндра. Затем аналогично проектируют на
боковую поверхность цилиндра все остальные зоны.
Р
Осевые меридианы зон
Х0
Х0
Х0
O
Зона на цилиндре
0
Q1
Q
Р1
Зона на шаре
1-я
0
0
2-я
3-я
Зоны на плоскости

11.

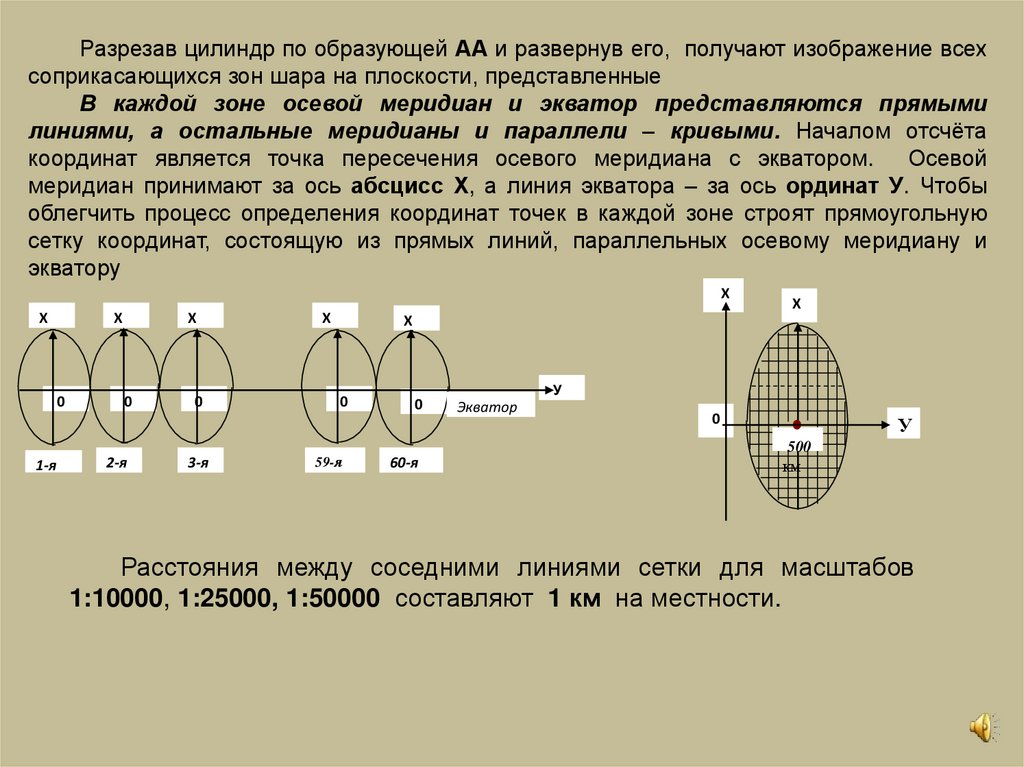
Разрезав цилиндр по образующей АА и развернув его, получают изображение всех
соприкасающихся зон шара на плоскости, представленные
В каждой зоне осевой меридиан и экватор представляются прямыми
линиями, а остальные меридианы и параллели – кривыми. Началом отсчёта
координат является точка пересечения осевого меридиана с экватором.
Осевой
меридиан принимают за ось абсцисс Х, а линия экватора – за ось ординат У. Чтобы
облегчить процесс определения координат точек в каждой зоне строят прямоугольную
сетку координат, состоящую из прямых линий, параллельных осевому меридиану и
экватору
Х
Х
Х
0
1-я
Х
0
2-я
0
3-я
Х
Х
Х
0
59-я
0
60-я
У
Экватор
0
У
500
км
Расстояния между соседними линиями сетки для масштабов
1:10000, 1:25000, 1:50000 составляют 1 км на местности.

12.

Чтобы не было отрицательных значений ординат, точке пересечения осевого меридиана и
экватора приписывают 500 км т.е. начало отсчёта координат в зоне искусственно переносят к
западу на 500 км. Вследствие этого все точки в зоне будут иметь только положительные значения.
Такие координаты называют преобразованными.
Преобразованная ордината начинается с номера зоны, затем к нему добавляется расстояние от
нулевого начала отсчёта в зоне до данной точки. Например, если точка расположена в 5-й зоне на
расстоянии 43500 м к западу от осевого меридиана, то её ордината У = 5 + ( 500 км – 43 км 500 м )
= 5456500 м. Абсцисса этой точки выражается расстоянием от экватора до данной точки, например,
Х = 6355245 м.
Вполне понятно, что вследствие проектирования зон на поверхность цилиндра имеют место
погрешности в изображении зон на цилиндре ( на цилиндре зоны шире , чем на шаре ). Кроме того,
при изображении зон на плоскости имеют место искажения длин линий в зависимости от их удаления
от осевого меридиана. При этом они будут максимальными на границах зон. Вследствие этих причин
картографирование земной поверхности выполняется с некоторыми погрешностями. Каковы же их
величины?
Из картографии известно, что на поверхности шара длина линии S при изображении её на
плоскости получит искажение Δ S , выражаемое формулой
Δ S = У2m S / 2R2,
где Уm - среднее значение ординат начальной У1 и конечной У2 точек линии ;
R – радиус Земли ( R = 6371 км ).
Полагая, что наибольшее значение Уm = 250 км, R = 6371 км , ошибка в измеренной линии
Δ S при длине линии S = 500 м не превысит 50 см. Это позволяет утверждать, что
картографирование в проекции Гаусса может осуществляться с достаточно высокой точностью, с
искажениями, практически не влияющими на точность изображения местности на карте.

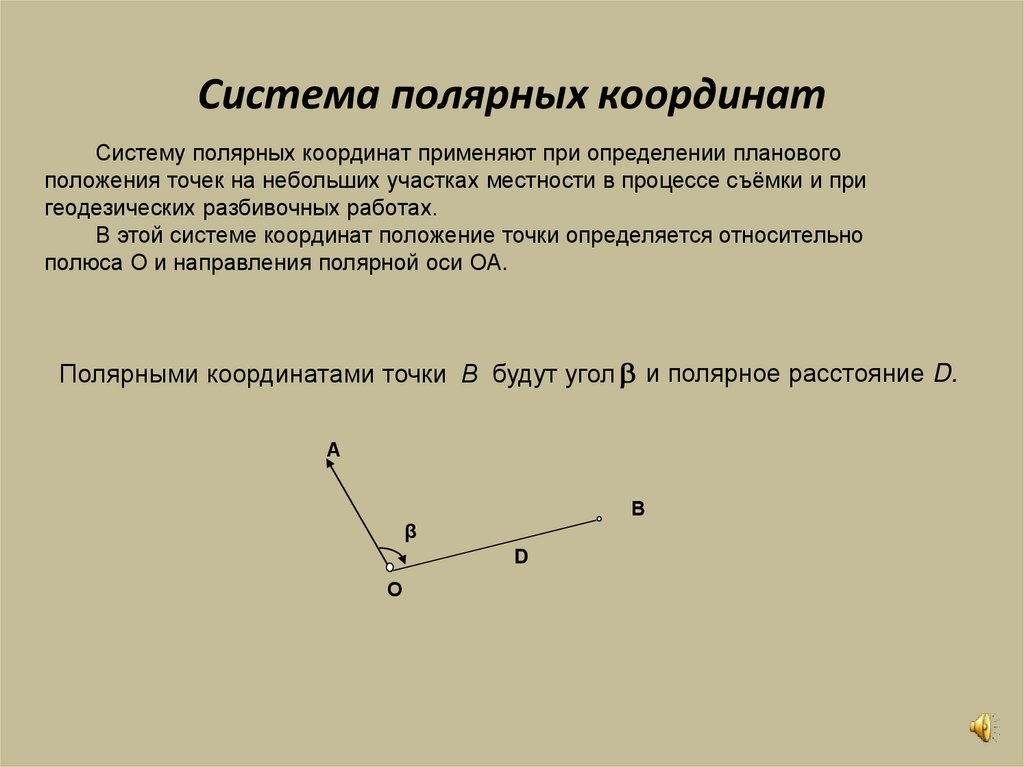
13. Система полярных координат

Систему полярных координат применяют при определении планового
положения точек на небольших участках местности в процессе съёмки и при
геодезических разбивочных работах.
В этой системе координат положение точки определяется относительно
полюса О и направления полярной оси ОА.
Полярными координатами точки В будут угол и полярное расстояние D.
А
В
β
D
О

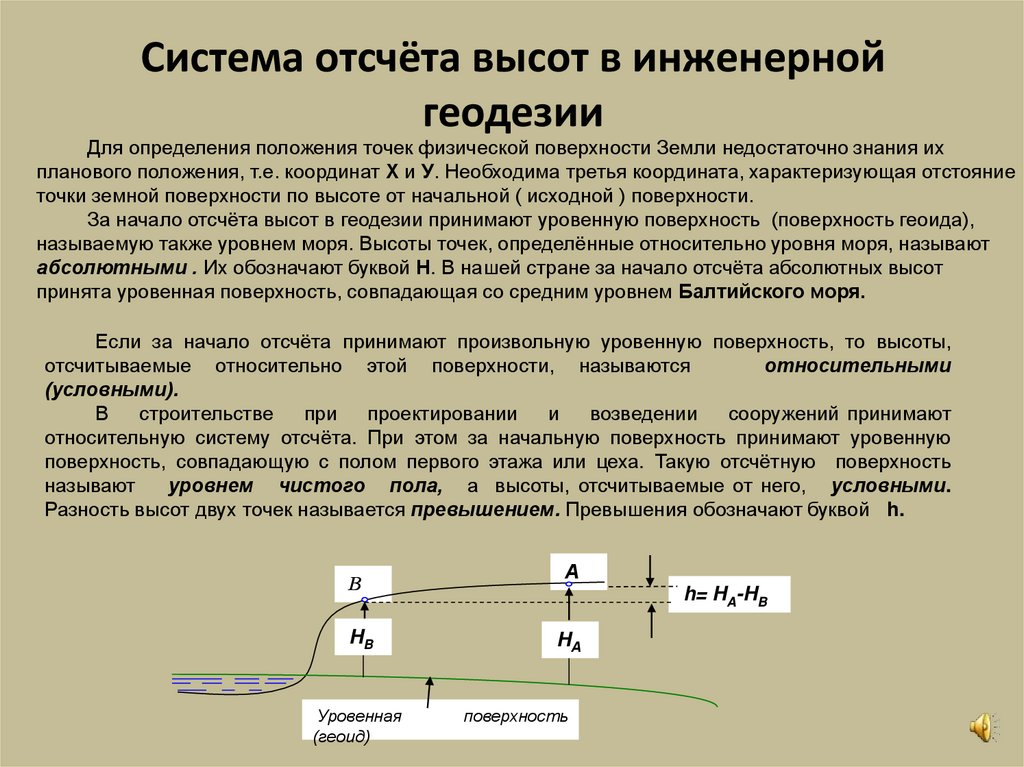
14. Система отсчёта высот в инженерной геодезии

Для определения положения точек физической поверхности Земли недостаточно знания их
планового положения, т.е. координат Х и У. Необходима третья координата, характеризующая отстояние
точки земной поверхности по высоте от начальной ( исходной ) поверхности.
За начало отсчёта высот в геодезии принимают уровенную поверхность (поверхность геоида),
называемую также уровнем моря. Высоты точек, определённые относительно уровня моря, называют
абсолютными . Их обозначают буквой Н. В нашей стране за начало отсчёта абсолютных высот
принята уровенная поверхность, совпадающая со средним уровнем Балтийского моря.
Если за начало отсчёта принимают произвольную уровенную поверхность, то высоты,
отсчитываемые относительно этой поверхности, называются
относительными
(условными).
В
строительстве
при
проектировании
и
возведении
сооружений принимают
относительную систему отсчёта. При этом за начальную поверхность принимают уровенную
поверхность, совпадающую с полом первого этажа или цеха. Такую отсчётную поверхность
называют
уровнем чистого пола, а высоты, отсчитываемые от него, условными.
Разность высот двух точек называется превышением. Превышения обозначают буквой h.
В
HB
Уровенная
(геоид)
А
h= HA-HB
HА
поверхность