ЭЦП и алгоритмы ЭЦП для ДО

1. Электронная цифровая подпись (ЭЦП) и алгоритмы ЭЦП

2. Электронная Цифровая Подпись (ЭЦП)

• Электронная Цифровая Подпись (ЭЦП)
является полным электронным аналогом
обычной
подписи
на
бумаге,
но
реализуется не с помощью графических
изображений,
а
с
помощью
математических
преобразований
над
содержимым документа. Особенности
математического алгоритма создания и
проверки ЭЦП гарантируют невозможность
подделки такой подписи

3.

ЭЦП представляет собой определенную
последовательность символов, которая
формируется
в
результате
преобразования исходного документа
(или любой другой информации) при
помощи специального программного
обеспечения.
ЭЦП
добавляется
к
исходному документу при пересылке. ЭЦП
является уникальной для каждого
документа и не может быть перенесена на
другой документ.

4. Хэш-функция

• Хэш-функция предназначена для сжатия
подписываемого документа М до нескольких
десятков или сотен бит.
• Хэш-функция h(•) принимает в качестве аргумента
сообщение (документ) М произвольной длины и
возвращает хэш-значение h(М)=Н фиксированной
длины. Обычно хэшированная информация
является сжатым двоичным представлением
основного сообщения произвольной длины.
• Значение хэш-функции h(М) сложным образом
зависит от документа М и не позволяет
восстановить сам документ М.

5. Условия для хэш-функции

• хэш-функция должна быть чувствительна к
всевозможным изменениям в тексте М, таким как
вставки, выбросы, перестановки и т.п.;
• хэш-функция должна обладать свойством
необратимости, то есть задача подбора документа
М', который обладал бы требуемым значением
хэш-функции, должна быть вычислительно
неразрешима;
• вероятность того, что значения хэш-функций двух
различных документов (вне зависимости от их
длин) совпадут, должна быть ничтожно мала.

6.

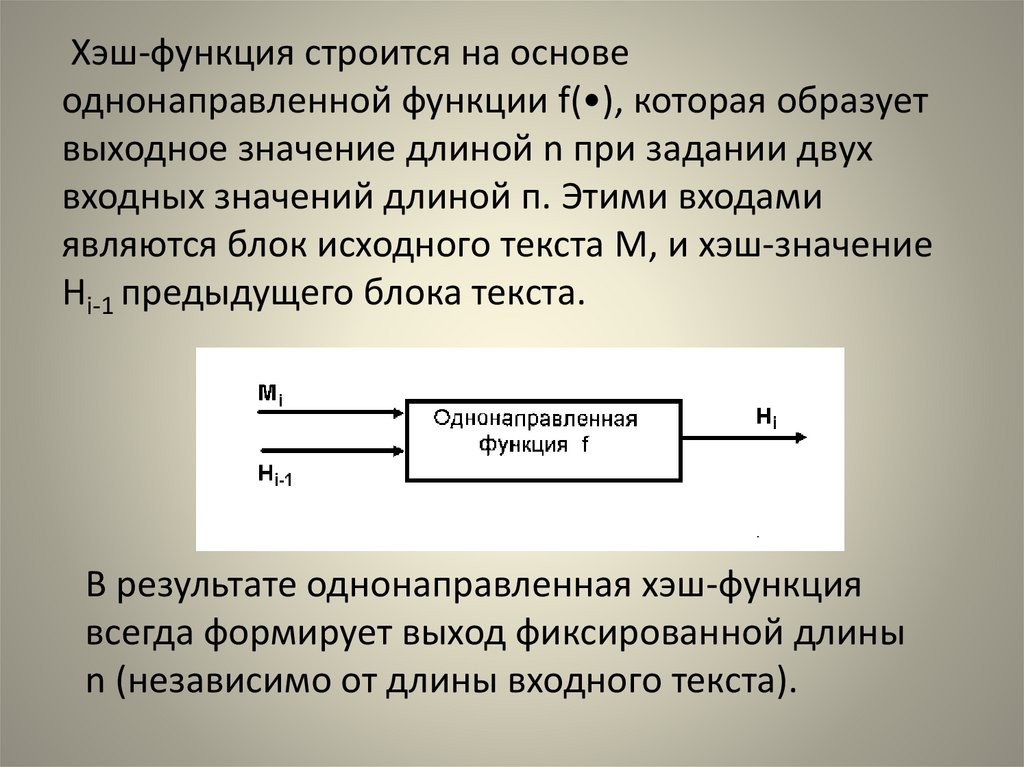
Хэш-функция строится на основе
однонаправленной функции f(•), которая образует
выходное значение длиной n при задании двух
входных значений длиной п. Этими входами
являются блок исходного текста М, и хэш-значение
Ні-1 предыдущего блока текста.
В результате однонаправленная хэш-функция
всегда формирует выход фиксированной длины
n (независимо от длины входного текста).

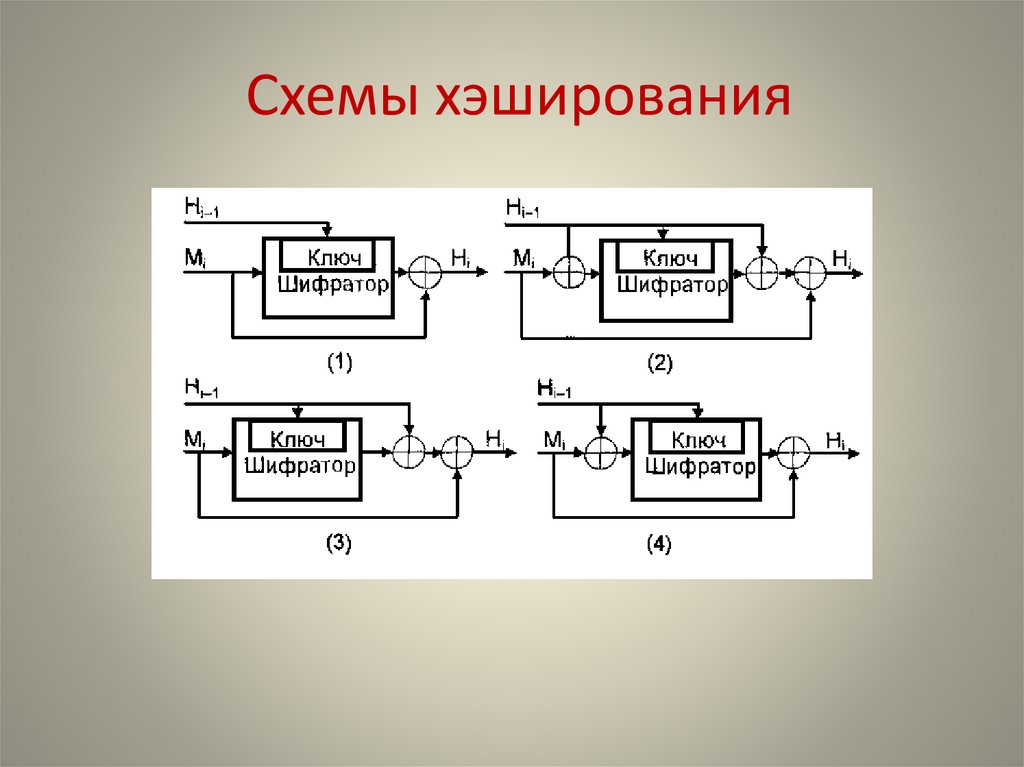
7.  Схемы хэширования

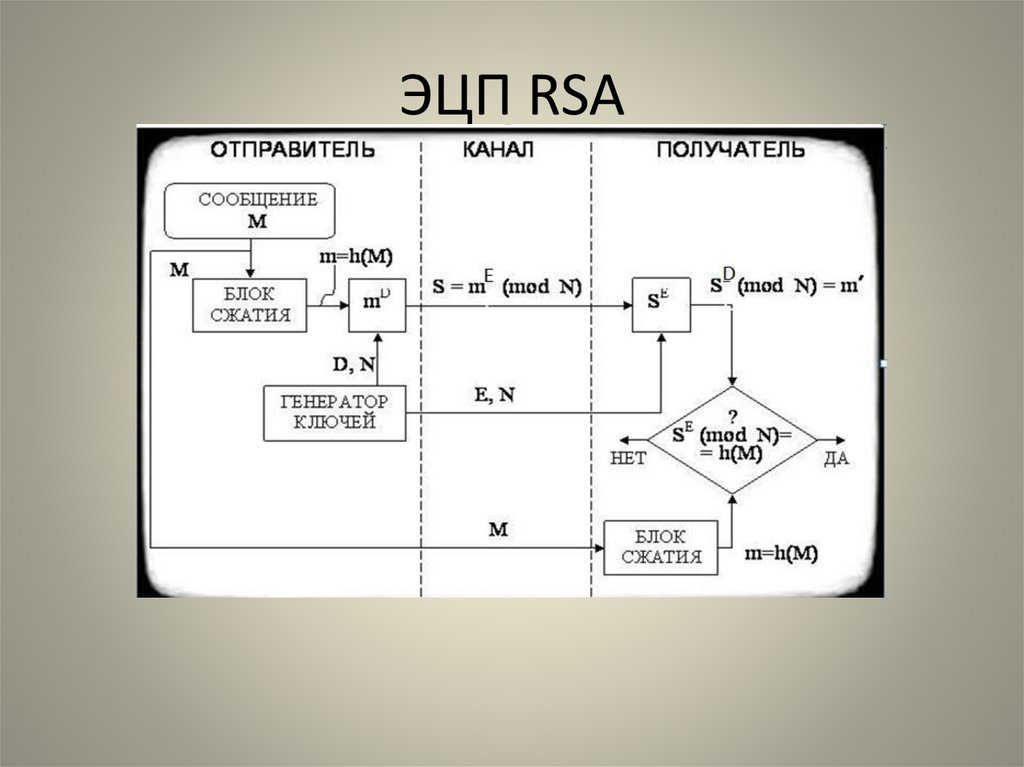
Схемы хэширования

8. ЭЦП RSA

9. Алгоритм ЭЦП RSA

1. Выбираются два больших и взаимно-простых числа p и q;
2. Вычисляем модуль RSA. n=p*q;
• Определяем функцию Эйлера: φ(n)=(p-1)(q-1); (m – было для
простого шифрования)
• Выбираем секретный ключ e с учетом условий: 1<e≤φ(n),HOD(e,
φ(n))=1; т.е секретный ключ e должен быть взаимопростым с φ(n)
• Определяем открытый ключ d, с учетом условий: d<n, e*d ≡
1(mod φ(n)).
•т.е (e*d) mod φ(n) = 1

10. Алгоритм ЭЦП RSA

Формирование ЭЦП
1. Вычисляем хеш сообщения М: m = h(M).
2. Шифруем хеш сообщения на секретном ключе абонента – отправителя и
отправляем полученную ЭЦП, S = mе (mod n), абоненту – получателю вместе с
открытым текстом документа М.
Проверка подлинности подписи на стороне абонента – получателя
1. Расшифровываем ЭЦП S c помощью открытого ключа d и получаем таким
образом, доступ к хеш – значению, присланному абонентом – отправителем.
m = Sd (mod n)
2. Вычисляем хеш открытого документа m’= h(M).
3. Сравниваем хеш – значения m и m’, и делаем вывод, что ЭЦП достоверна, если
m = m’.

11. Упрощённая хеш-функция квадратичной свёртки

H0 = 0
n – открытый ключ автора сообщения
Mi – коды символов сообщения, открытого
или предварительно зашифрованного.
После обработки последнего символа
получаем хеш-образ всего сообщения H .

12. Пример ЭЦП RSA 1 этап, это генерация ключей

Подбираем p и q – простые числа.
p=5
q = 11
n = p*q = 55
Находим φ(n) наша(m) по формуле:
φ(n) = (p-1)*(q-1) = 4*10 = 40
Выбираем простое число e взаимно простое к φ(n)
e = 7 это закрытый ключ
Находим d из равенства (d*e) mod φ(n) = 1
d = 23 это открытый ключ

13. Пример ЭЦП RSA 2 этап, хеш-функция

Будем создавать ЭЦП для слова секреты.
Надо перевести в символы
Секреты = 19, 6, 12, 18, 6, 20, 29

14. Пример ЭЦП RSA 2 этап, хеш-функция

Для нахождения хешированных значений цифр из букв по формулой:
Hi = (Hi-1 + Mi)^2 mod n
Для начального значения H0 возьмем 1.
H(C) = (H0 + M(C))^2 mod n = (1 + 19)^2 mod 55 = 15
H(E) = (15 + 6)^2 mod 55 = 1
H(K) = (1 + 12)^2 mod 55 = 4
H(P) = (4 + 18)^2 mod 55 = 44
H(E) = (44 + 6)^2 mod 55 = 25
H(T) = (25 + 20)^2 mod 55 = 45
H(Ы) = (45 + 29)^2 mod 55 = 31
H образ = 31

15. Пример ЭЦП RSA 3 этап, создание ЭЦП и проверка

S = H (образ) ^ e mod n = 31^ 7 mod 55 = 26 СЕКРЕТЫ
S – цифровая подпись, которую получили из формулы.
Проверим цифровую подпись по формуле:
H’ = S^d mod n = 26^23 mod 55 = 31
H(образ) = H’ то ЭЦП была верно зашифрована.

16. Алгоритм ЭЦП ГОСТ

Формирование ЭЦП
В нем используются следующие параметры:
р - большое простое число (длиной от 509 до 512 бит
либо от 1020 до 1024 бит);
q - простой сомножитель числа (р -1), имеющий
длину 254...256 бит;
а - любое число, меньшее (р-1), причем такое, что
а^q mod p=1;
х - некоторое число, меньшее q;
у = а^x mod р.

17. Алгоритм ЭЦП ГОСТ

Формирование ЭЦП
Первые три параметра р, q и а являются
открытыми и могут быть общими для всех
пользователей сети. Число х является секретным
ключом.
• Число у является открытым ключом. Чтобы
подписать некоторое сообщение m, а затем
проверить подпись, выполняются следующие
шаги.

18. Алгоритм ЭЦП ГОСТ

Формирование ЭЦП
1. Пользователь А генерирует случайное число
k, причем k<q.
2. Пользователь А вычисляет значения
r = (аk mod p) mod q,
s = (х * r + k (Н(m))) mod p.
Если Н(m) mod q=0, то значение Н(m) mod q
принимают равным единице. Если r=0, то
выбирают другое значение k и начинают снова.

19. Алгоритм ЭЦП ГОСТ

Формирование ЭЦП
Цифровая подпись представляет собой два числа:
r и s Пользователь А отправляет эти числа пользователю В.
3. Пользователь В проверяет полученную подпись, вычисляя
w = Н(m)q-2 mod q,
u1 = (s * w) mod q,
u2 = ((q-r) * w) mod q,
v = ((аu1 * уu2 ) mod р) mod q.
Если v = r, то подпись считается верной

20. Пример ЭЦП ГОСТ 1 этап, это генерация ключей

Подбираем p и q – простые числа.
p = 11
q=5
n = p*q = 55
Подбираем такое число a из равенства а^q mod p=1
а - любое число в диапазоне 1<a<p-1, а = 4
Подбираем закрытый ключ x из диапазона 0<x<q
x=2

21. Пример ЭЦП ГОСТ

1 этап, это генерация ключей
Формируем открытый ключ y по формуле
y = a^x mod p
y = a^x mod p = 4 ^ 2 mod 11 = 5
Подбираем k из неравенств 0<k<q
k=3

22. Пример ЭЦП ГОСТ 2 этап, хеш-функция

Будем создавать ЭЦП для слова секреты.
Надо перевести в символы
Секреты = 19, 6, 12, 18, 6, 20, 29

23. Пример ЭЦП ГОСТ 2 этап, хеш-функция

Для нахождения хешированных значений цифр из букв по формулой:
Hi = (Hi-1 + Mi)^2 mod n
Для начального значения H0 возьмем 1.
H(C) = (H0 + M(C))^2 mod n = (1 + 19)^2 mod 55 = 15
H(E) = (15 + 6)^2 mod 55 = 1
H(K) = (1 + 12)^2 mod 55 = 4
H(P) = (4 + 18)^2 mod 55 = 44
H(E) = (44 + 6)^2 mod 55 = 25
H(T) = (25 + 20)^2 mod 55 = 45
H(Ы) = (45 + 29)^2 mod 55 = 31
H образ = 31

24. Пример ЭЦП ГОСТ

3 этап, создание ЭЦП и проверка
Создаем (r;s) – ЭЦП
r = (a^k mod p) mod q = (4^3 mod 11) mod 5 = 4
s = (k*H(m) + x*r) mod q = (3*31 + 2*4) mod 5 = 1
Проверим цифровую подпись по формуле:

25. Пример ЭЦП ГОСТ

3 этап, создание ЭЦП и проверка
Пользователь В проверяет полученную подпись, вычисляя
w = Н(m)q-2 mod q= 31^3 mod 5= 1
u1 = (s * w) mod q = 1*1 mod 5 =1
u2 = ((q-r) * w) mod q = 1*1 mod 5 =1
v = ((аu1 * уu2 ) mod р) mod q
= ((4^1* 5^1) mod 11) mod 5= 4
Если v = r, то подпись считается верной