Презентация к уроку геометрии по теме _Прямые параллельные и перпендикулярные к

1. Прямые параллельные и перпендикуляр­ные к плоскости

Прямые параллельные и
перпендикулярные к
плоскости
Подготовила:
учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42»
Рыбина М.В.

2. Определение

Прямая называется перпендикулярной к
плоскости, если она перпендикулярна
любой прямой, лежащей в этой
плоскости.
a a b, a c, a d

3. Перпендикулярность прямой и плоскости в жизни

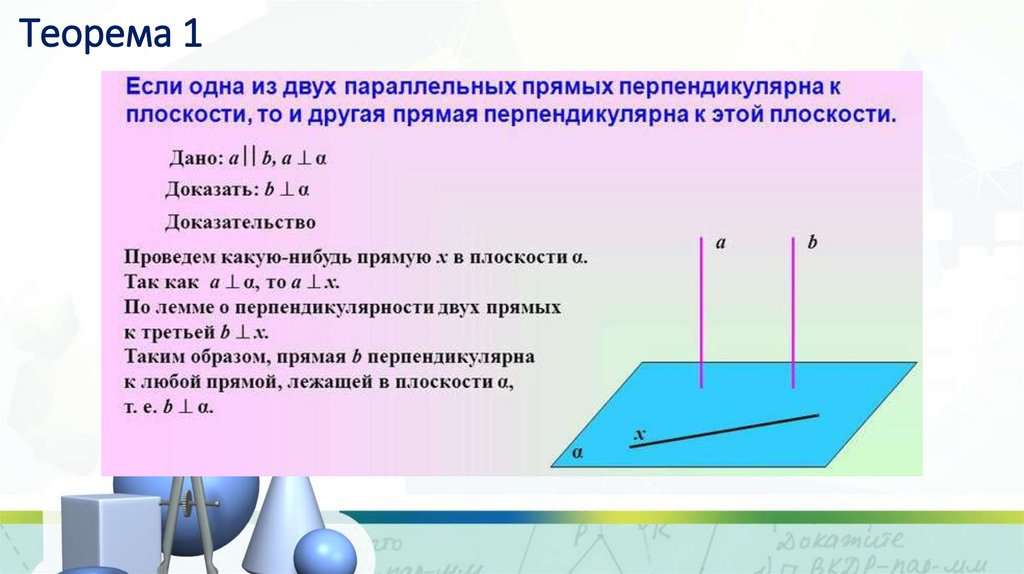
4. Теорема 1

5. Теорема 2

Если две прямые перпендикулярны к плоскости, то
они параллельны.
Доказательство
Рассмотрим прямые a и b, перпендикулярные к
плоскости . Докажем, что a b. Через любую точку
М прямой b, проведем прямую b1 , параллельную
прямой a.По предыдущей теореме b1 . Докажем, что
прямая b1 совпадет с прямой b.Допустим, что прямые b
и b1 не совпадают. Тогда в плоскости , содержащей
прямые b и b1 , через точку м проходят две прямые,
перпендикулярные к прямой с, по которой
пересекаются плоскости и . Но это невозможно.
Следовательно, a b.

6. Задача № 1

Пользуясь изображением куба , запишите:
1) плоскость, проходящую через точку М прямой
АМ и перпендикулярную ей;
2) прямую, перпендикулярную плоскости АВС и
проходящую через точку D;
3) прямую, перпендикулярную плоскости АВС и
проходящую через точку N;
4) плоскость, перпендикулярную прямой BD;
5) прямые, перпендикулярные плоскости АМС;
6) плоскости, перпендикулярные прямой DC.
1) (MNK); 2) KD; 3) BN; 4) (ACM);
5) BD и KN; 6) (ADK) и (BCL).

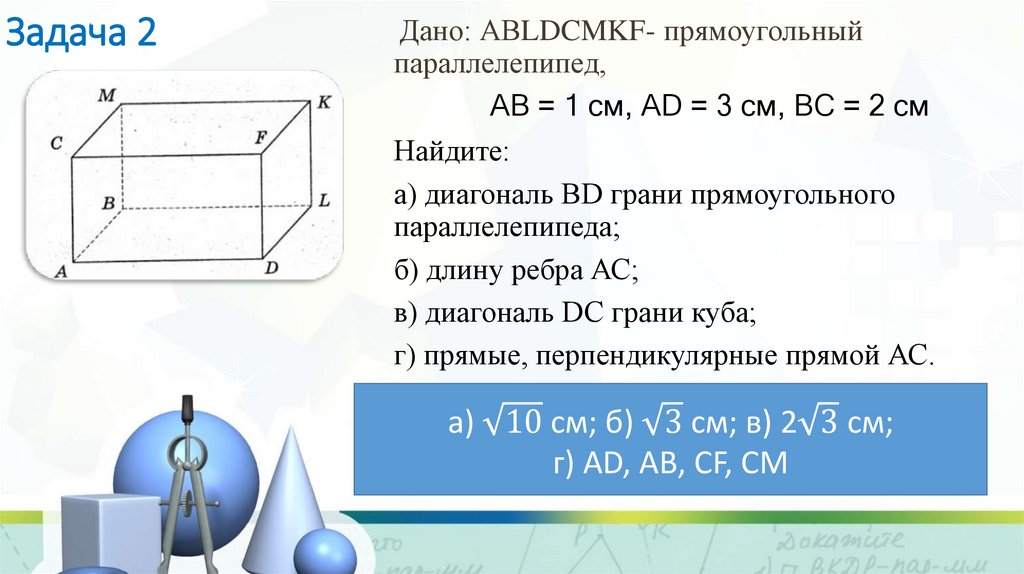
7. Задача 2

Дано: АВLDCMKF- прямоугольный
параллелепипед,
АВ = 1 см, AD = 3 см, ВС = 2 см
Найдите:
а) диагональ BD грани прямоугольного
параллелепипеда;
б) длину ребра АС;
в) диагональ DC грани куба;
г) прямые, перпендикулярные прямой АС.
а) 10 см; б) 3 см; в) 2 3 см;
г) AD, АВ, CF, СМ

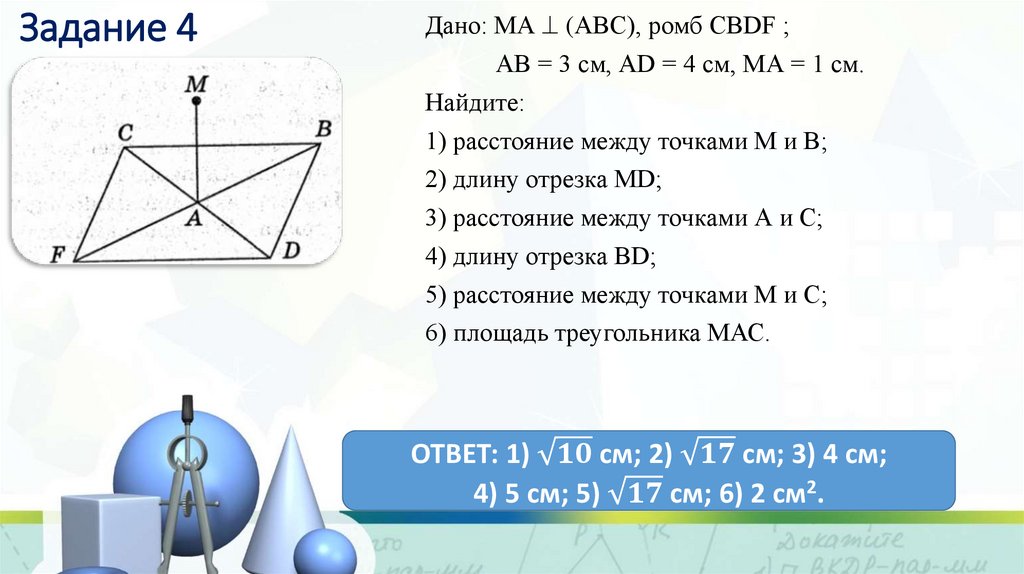
8. Задача 3

Дано: МА АВ, МА АС; ВАС = 90°
АF – медиана треугольника АВС;
АВ = 5 см, АС = 12 см.
Найти:
1) Каково взаимное расположение прямой МА и плоскости
АВС?
2) Каково взаимное расположение прямой МА и прямой
АF?
3) Верно ли, что АF ВС?
4) Найдите длину гипотенузы ВС.
5) Найдите длину медианы АF.
6) Найдите длину отрезка МА, если МF = 7 см.
1) МА (АВС); 2) МА АF; 3) нет;
4) 13 см; 5) 6,5 см; 6)