Задачи для подготовки к ЕГЭ по математике (раздел С2)

1.

1

2.

Раздел 1. Угол между прямыми
Раздел 2. Угол между прямой и плоскостью
Раздел 3. Угол между двумя плоскостями
Раздел 4. Расстояние от точки до прямой
Раздел 5. Расстояние от точки до плоскости
Раздел 6. Расстояние между двумя прямыми

3.

Раздел 1
Угол между
прямыми
3

4.

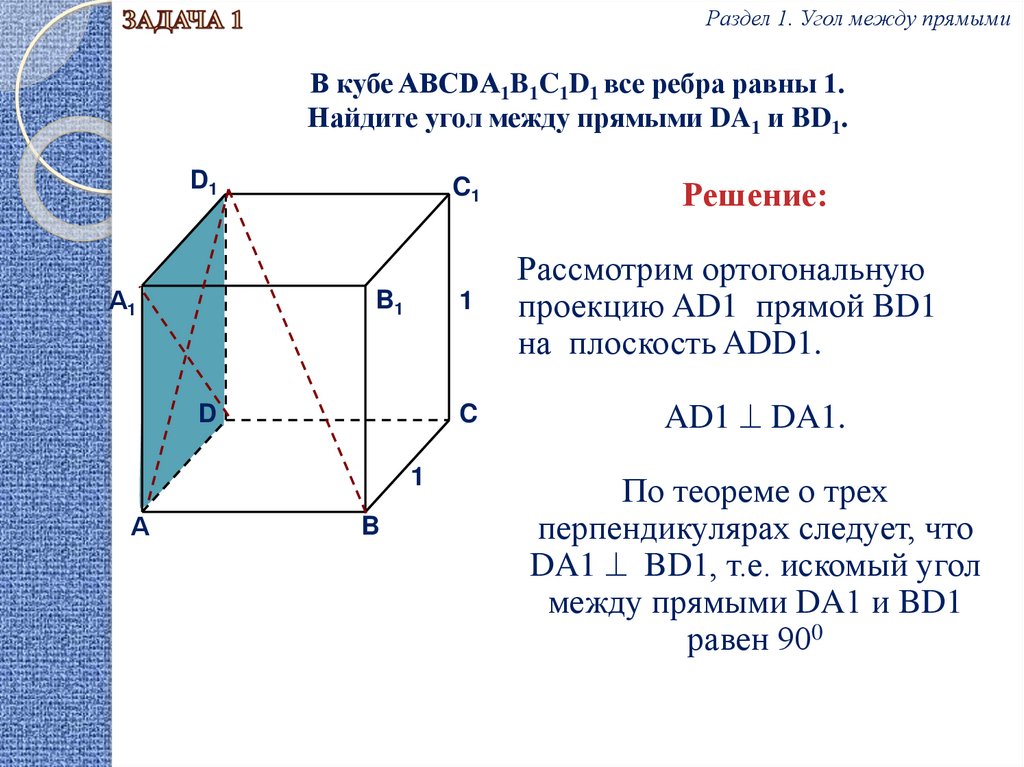
Раздел 1. Угол между прямыми
В кубе ABCDA1B1C1D1 все ребра равны 1.
Найдите угол между прямыми DA1 и BD1.
D1
А1
C1
B1
1
C
D
1
А
B
Решение:
Рассмотрим ортогональную
проекцию AD1 прямой BD1
на плоскость ADD1.
AD1 DA1.
По теореме о трех
перпендикулярах следует, что
DA1 BD1, т.е. искомый угол
между прямыми DA1 и BD1
равен 900

5.

Раздел 1. Угол между прямыми
В правильной шестиугольной призме A...F1, все ребра которой
равны 1, найдите косинус угла между прямыми АВ1и ВС1.
Решение:
Угол между скрещивающимися прямыми - это угол между
параллельными им прямыми, проходящими через одну точку.
ОС1||АВ1, так как четырехугольник АВ1С1О является
параллелограммом.
Поэтому искомый угол - это угол
ОС1В. Из ОС1В по теореме
косинусов, получаем, что
cos OC1 B
2 2 1 3
0,75
2 2 2 4
(Т.к. ОВ=1, ВС1= 2, ОС1= 2)
Ответ: 0,75
5

6.

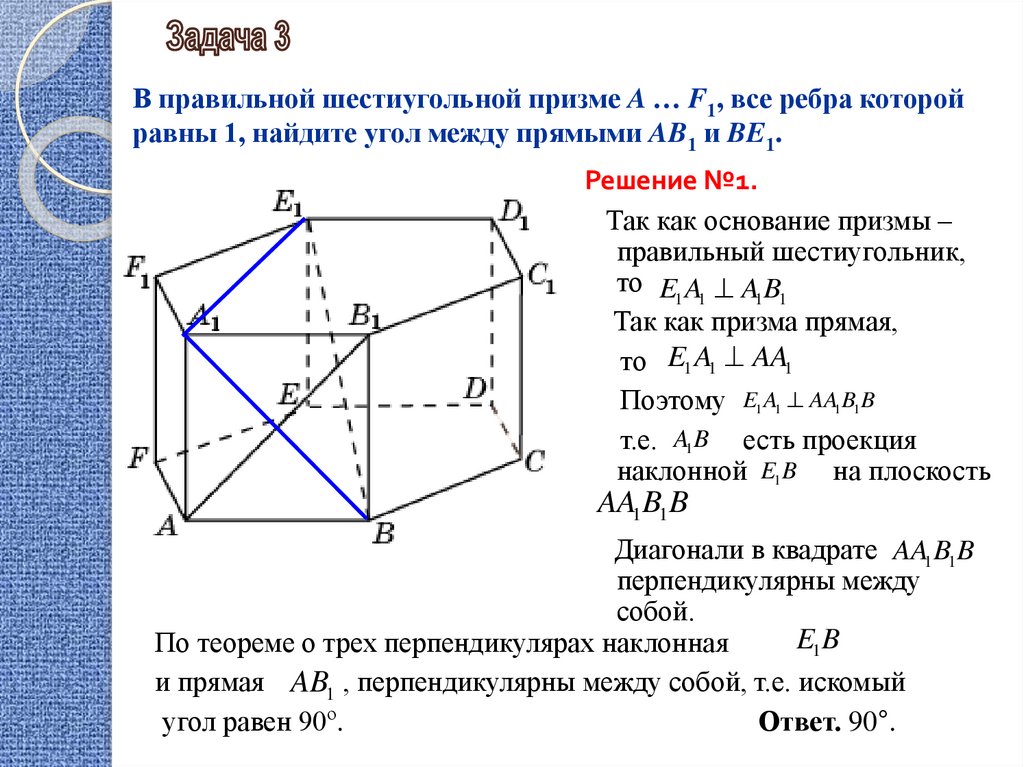
В правильной шестиугольной призме A … F1, все ребра которой
равны 1, найдите угол между прямыми AB1 и BE1.
Решение №1.
Так как основание призмы –
правильный шестиугольник,
то E1 A1 A1B1
Так как призма прямая,
то E1 A1 AA1
Поэтому E1 A1 AA1B1B
т.е. A1B есть проекция
наклонной E1B на плоскость
AA1B1B
Диагонали в квадрате AA1B1B
перпендикулярны между
собой.
E1B
По теореме о трех перпендикулярах наклонная
и прямая AB1 , перпендикулярны между собой, т.е. искомый
угол равен 90о.
Ответ. 90°.

7.

Раздел 2
Угол между
прямой и
плоскостью
7

8.

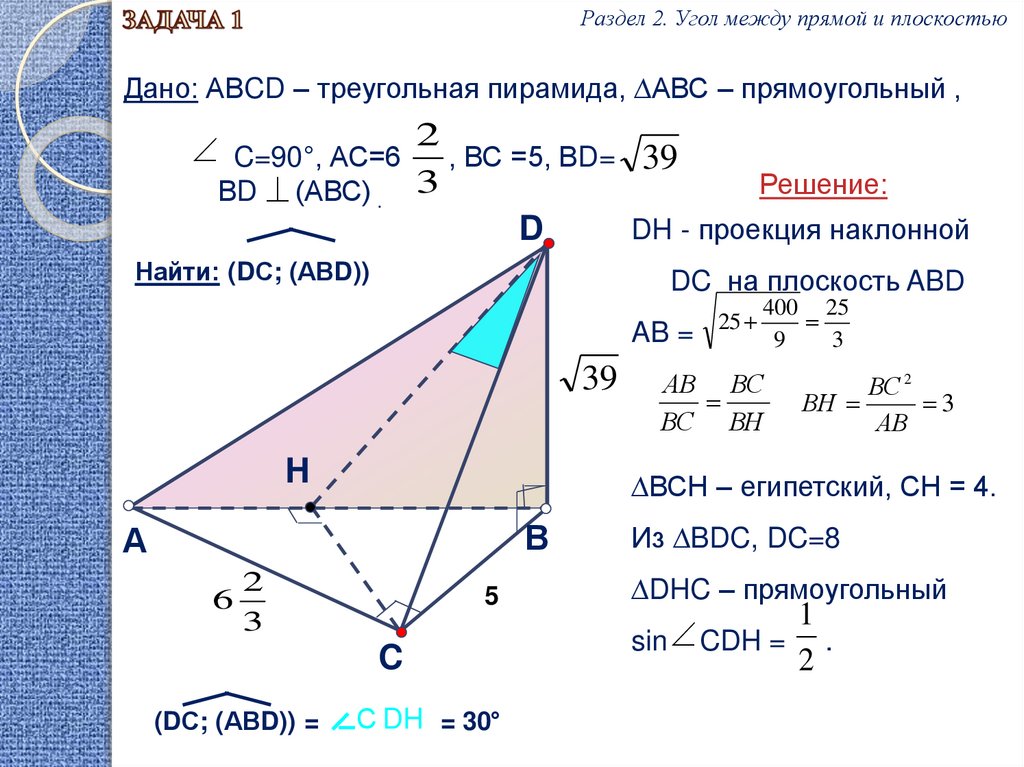
Раздел 2. Угол между прямой и плоскостью
Дано: АВCD – треугольная пирамида, ∆АВС – прямоугольный ,
C=90°, АС=6 2 , ВС =5, ВD= 39
Решение:
ВD (АВС) . 3
DH - проекция наклонной
D
Найти: (DС; (АВD))
DC на плоскость ABD
AB =
39
H
В
2
3
5
C
(DС; (АВD)) =
400 25
9
3
АВ ВС
ВС ВН
ВС 2
ВН
3
АВ
∆ВСН – египетский, СН = 4.
А
6
25
С DH = 30°
Из ∆BDC, DC=8
∆DHC – прямоугольный
1
sin CDH = .
2

9.

Раздел 2. Угол между прямой и плоскостью
А1
C1
Дано: АВСDFKA1B1C1D1F1K 1 –
правильная призма, АВ=4, AA1= 2 5
АА1 (АВС)
F1
K1
Т
B1
D1
B
Найти: (В1F; (BB1C1))
C
А
D
K
F
C
B
А
M
120°
4
D
4
K
F
Решение:
B1C проекция наклонной B1F на
плоскость BB1 C1C
DM = 2, CF= 2 16 4 4 3
∆CB1C1 – прямоугольный
B1 C = 20 16 6
∆ B1 CF – прямоугольный
tg FB1C
CF
4 3
3
B1C
6
3
В1F; (BB1C1))=
FB1C - 30°
9

10.

Раздел 2. Угол между прямой и плоскостью
В1
С1
А1
D1
5
Решение:
В
С
?
А
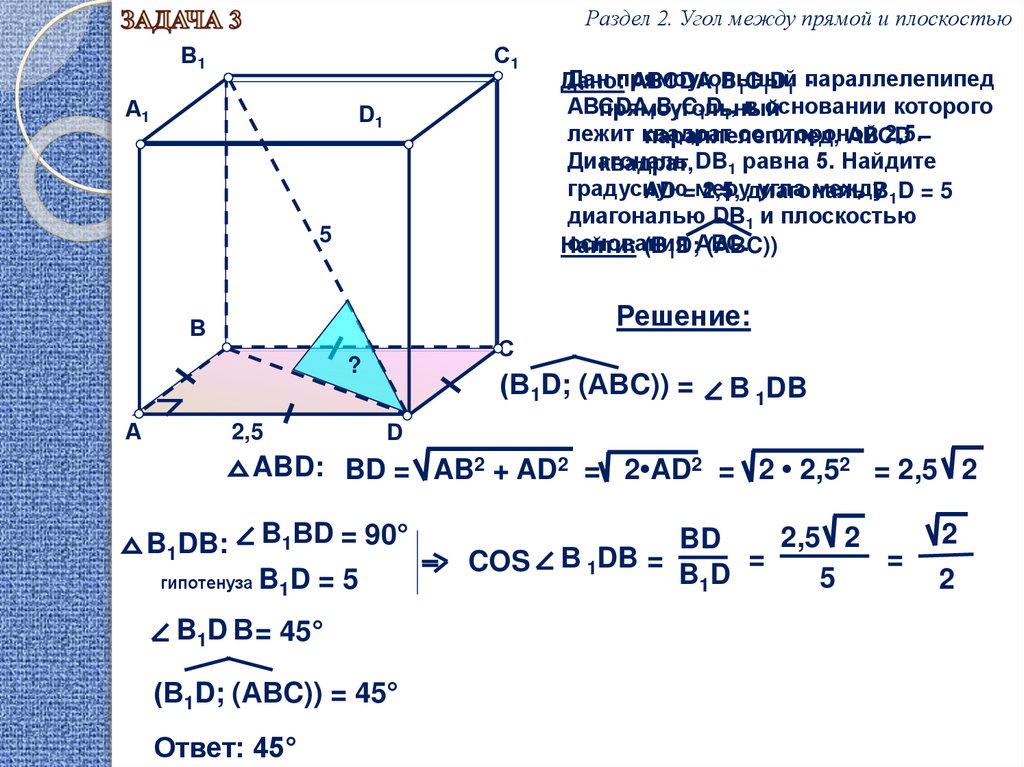
Дан прямоугольный
Дано:
АВСDA1B1C1D1 параллелепипед
АВСDA
прямоугольный
1B1C1D1, в основании которого
лежит квадрат
со стороной
2,5.–
параллелепипед,
АВСD
Диагональ
квадрат, DB1 равна 5. Найдите
градусную
угла между
AD =меру
2,5, диагональ
B1D = 5
диагональю DВ1 и плоскостью
основания
Найти:
(В1D;АВС.
(АВC))
2,5
(В1D; (АВC)) =
В 1DB
D
ABD: BD = AB2 + AD2 = 2•AD2 = 2 • 2,52 = 2,5 2
B1DB:
гипотенуза
B1ВD = 90°
B 1D = 5
B1D В = 45°
(В1D; (АВC)) = 45°
Ответ: 45°
COS
2,5 2
BD
В 1DB =
=
=
B 1D
5
2
2

11.

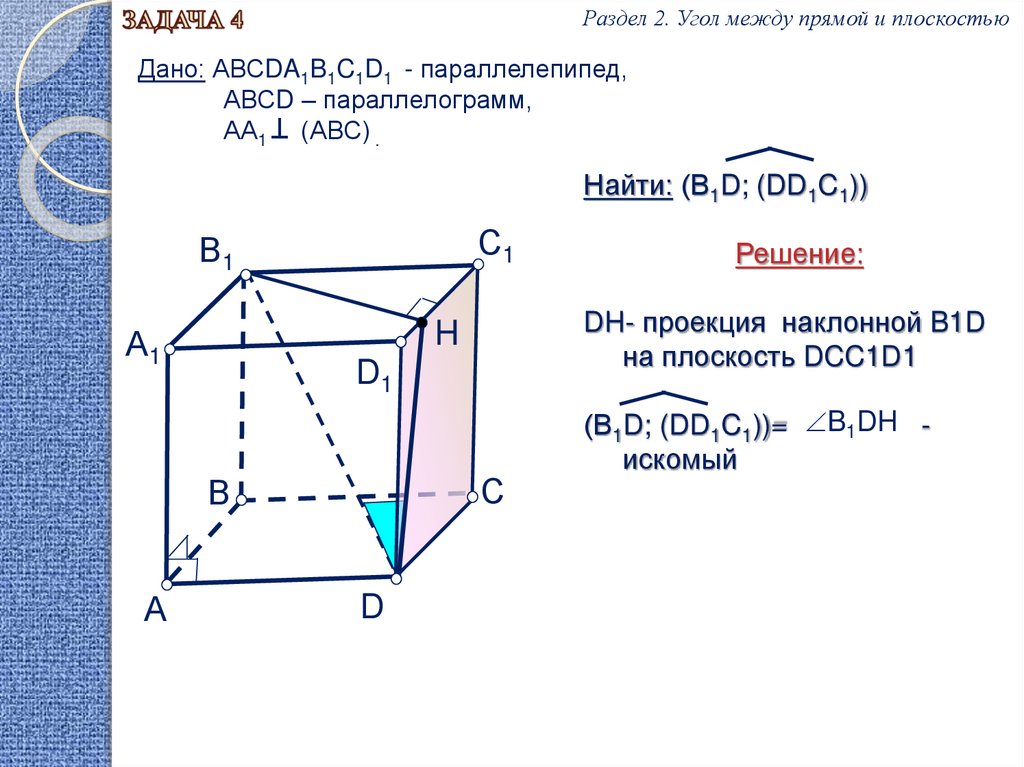
Раздел 2. Угол между прямой и плоскостью
Дано: АВСDA1B1C1D1 - параллелепипед,
АВСD – параллелограмм,
АА1 (АВС) .
Т
Найти: (В1D; (DD1C1))
С1
В1
D1
С
В
А
DH- проекция наклонной B1D
на плоскость DCC1D1
H
А1
D
Решение:
(В1D; (DD1C1))= B1DH искомый

12.

Раздел 3
Угол между
двумя
плоскостями
12

13.

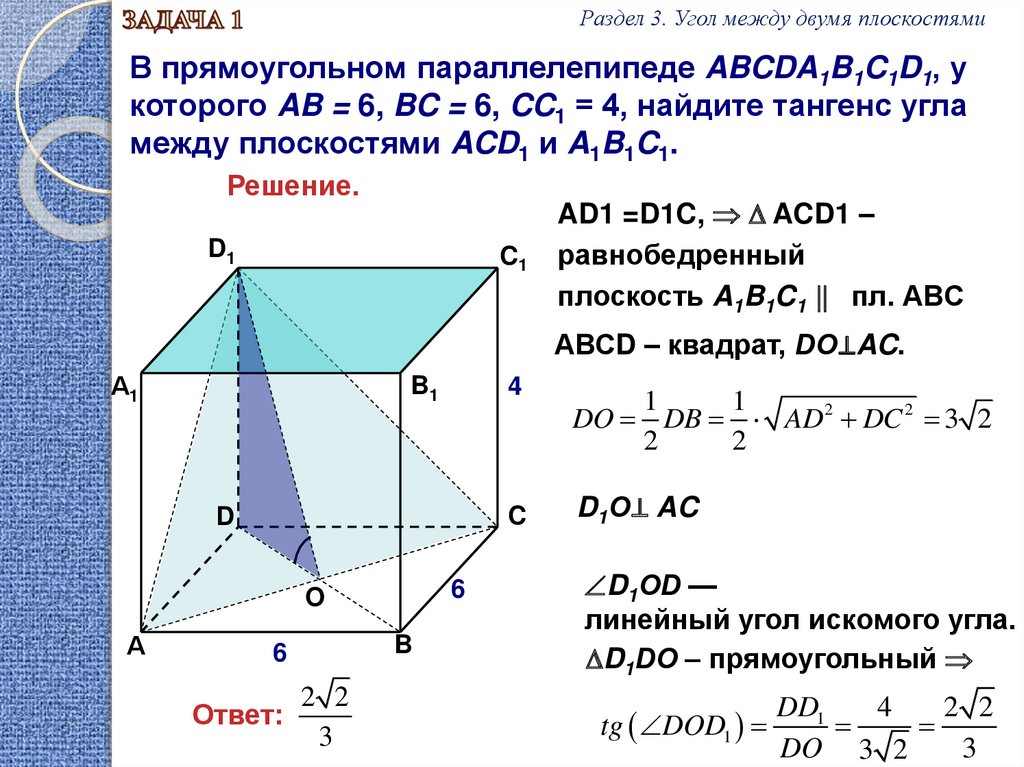
Раздел 3. Угол между двумя плоскостями
В прямоугольном параллелепипеде ABCDA1B1C1D1, у
которого AB = 6, BC = 6, CC1 = 4, найдите тангенс угла
между плоскостями ACD1 и A1B1C1.
Решение.
D1
C1
AD1 =D1C, ACD1 –
равнобедренный
плоскость A1B1C1 пл. АBC
АВСD – квадрат, DО⊥AC.
А1
B1
4
C
D
6
O
А
6
2 2
Ответ:
3
B
1
1
DO DB AD 2 DC 2 3 2
2
2
D1О⊥ AC
D1ОD —
линейный угол искомого угла.
D1DО – прямоугольный
tg DOD1
DD1
4
2 2
DO 3 2
3

14.

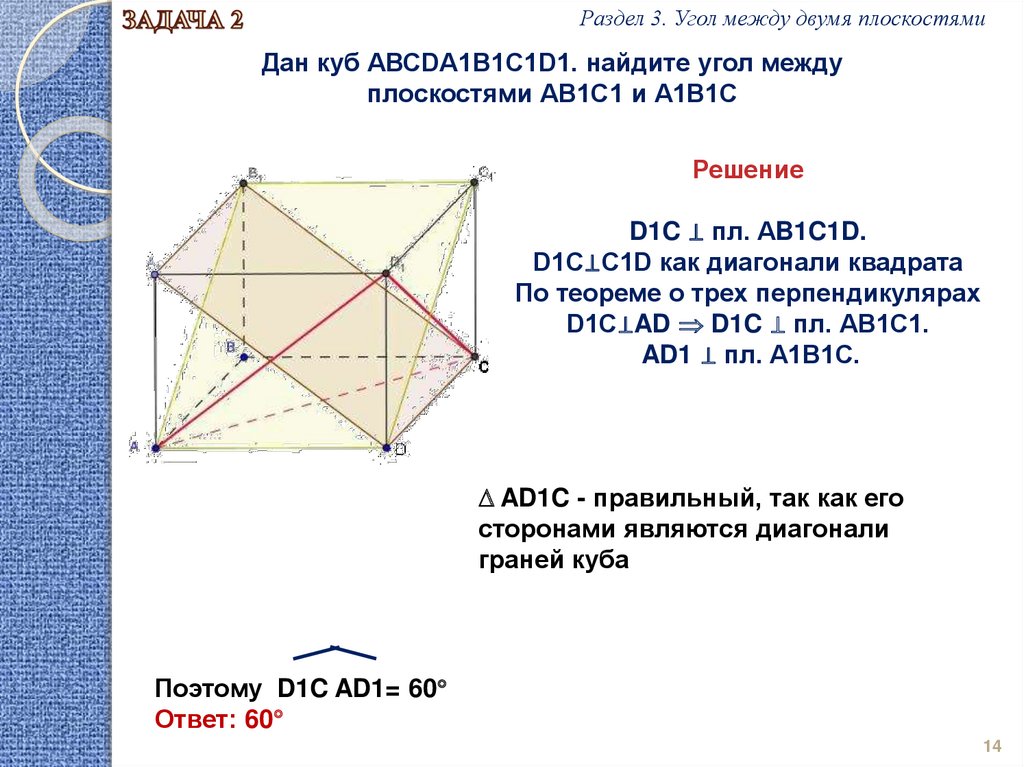
Раздел 3. Угол между двумя плоскостями
Дан куб АВСDA1B1C1D1. найдите угол между
плоскостями АВ1С1 и А1В1С
Решение
D1C ⊥ пл. АB1C1D.
D1С⊥C1D как диагонали квадрата
По теореме о трех перпендикулярах
D1С⊥AD D1C ⊥ пл. АВ1С1.
AD1 ⊥ пл. А1В1С.
AD1C - правильный, так как его
сторонами являются диагонали
граней куба
Поэтому D1C AD1= 60
Ответ: 60
14

15.

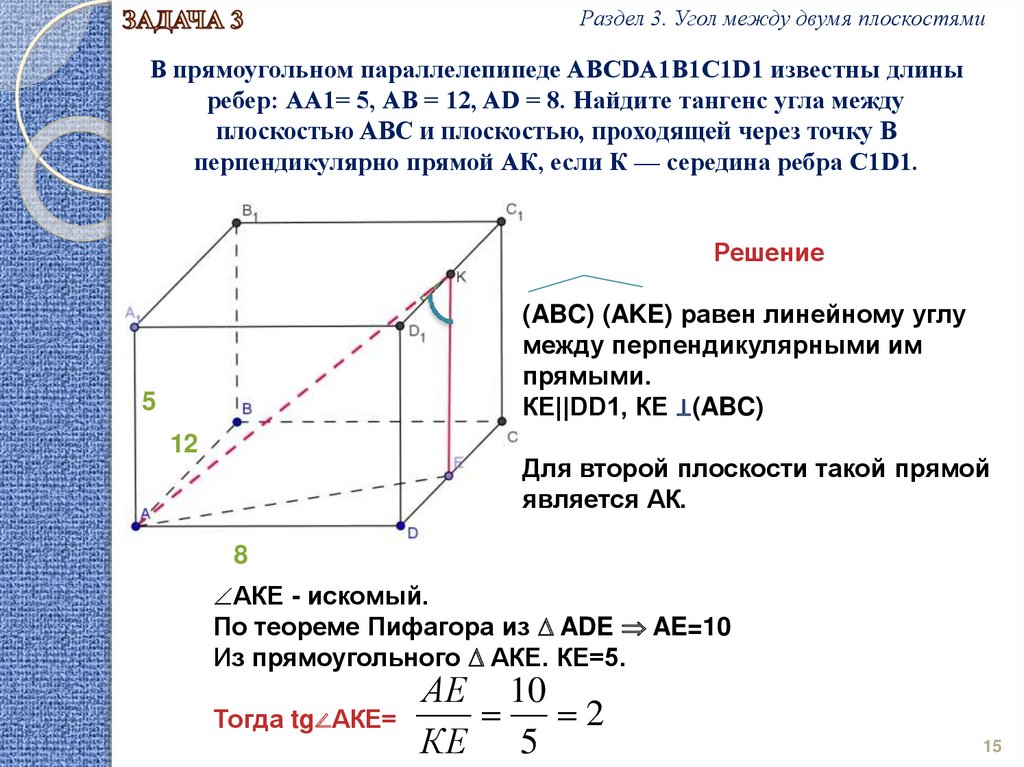
Раздел 3. Угол между двумя плоскостями
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины
ребер: АА1= 5, АВ = 12, AD = 8. Найдите тангенс угла между
плоскостью ABC и плоскостью, проходящей через точку В
перпендикулярно прямой АК, если К — середина ребра C1D1.
Решение
(ABC) (AKE) равен линейному углу
между перпендикулярными им
прямыми.
КЕ||DD1, КЕ ⊥(ABC)
5
12
Для второй плоскости такой прямой
является АК.
8
АКЕ - искомый.
По теореме Пифагора из ADE AE=10
Из прямоугольного АКЕ. КЕ=5.
Тогда tg∠АКЕ=
АЕ 10
2
КЕ 5
15

16.

Раздел 4
Расстояние
от точки
до прямой
16

17.

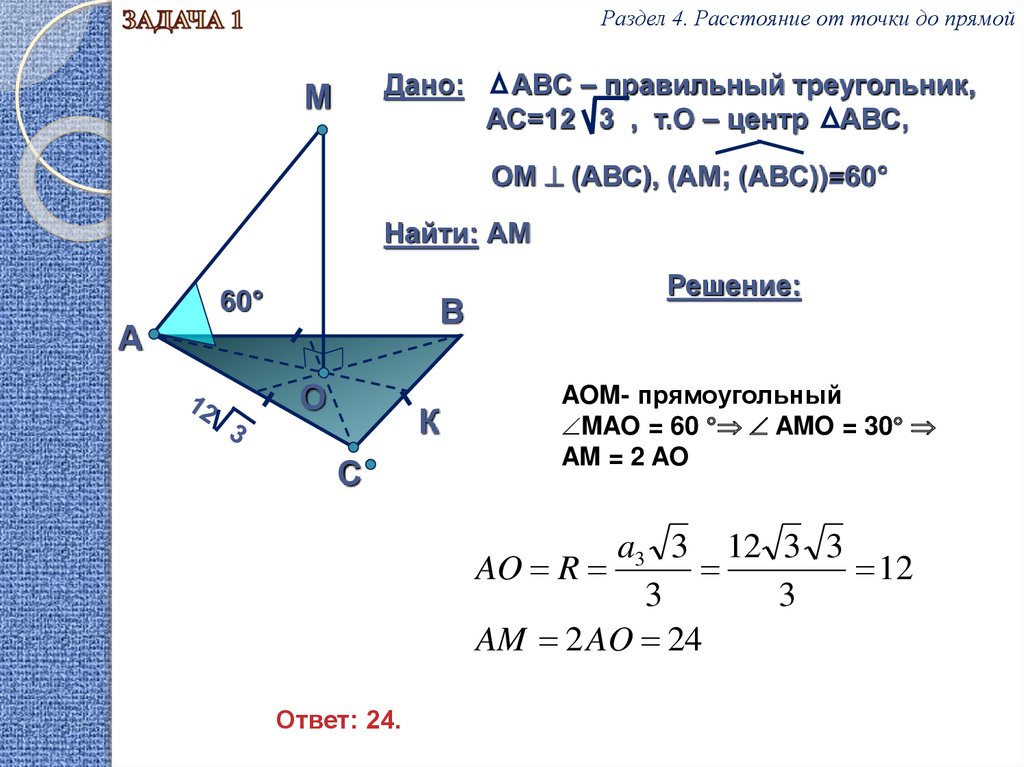
Раздел 4. Расстояние от точки до прямой
Дано:
М
АВС – правильный треугольник,
АС=12 3 , т.О – центр АВС,
ОМ (АВС), (АМ; (АВС))=60°
Найти: АМ
60°
В
А
О
К
С
Решение:
AOM- прямоугольный
MAO = 60 AMO = 30
AM = 2 AO
a3 3 12 3 3
AO R
12
3
3
AM 2 AO 24
Ответ: 24.

18.

Раздел 4. Расстояние от точки до прямой
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите
расстояние от точки С до прямой BD1 .
Решение.
D1
C1
А1
B1
BD1 (A1D1С В)
СМ BD1
1
В прямоугольном D1CB:
C
D
М
А
Ответ:
1
6
3
1
B
D1B=
3 , D1C= 2
sin B
CD1
2
BD1
3
В прямоугольном CMB:
CM
2
6
sin B
CM CB sin B 1
CB
3
3
18

19.

Раздел 5
Расстояние
от точки
до плоскости
19

20.

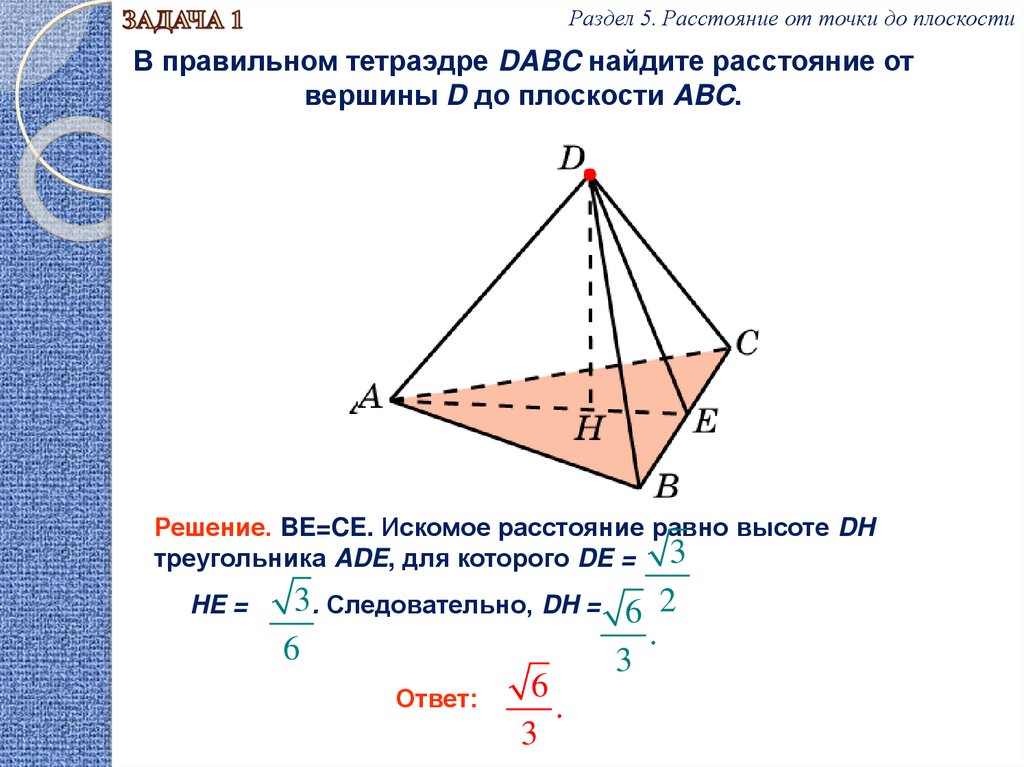
Раздел 5. Расстояние от точки до плоскости
В правильном тетраэдре DABC найдите расстояние от
вершины D до плоскости ABC.
Решение. BE=CE. Искомое расстояние равно высоте DH
треугольника ADE, для которого DE = 3
HE =
3 . Следовательно, DH = 6 2
.
6
3
6
Ответ:
.
3

21.

Раздел 5. Расстояние от точки до плоскости
В правильной 6-ой пирамиде SABCDEF, боковые
ребра которой равны 2, а ребра основания – 1,
найдите расстояние от точки A до плоскости SCE.
Решение. Точка G пересечение AD и CE. Искомое расстояние
равно высоте AH SAG
3 39
13, AG = 3 , SO =
Откуда
AH
=
.
3.
13
2
2
Ответ: 3 39 .
13
SA = 2, SG =
2

22.

Раздел 6
Расстояние
между двумя
прямыми
22

23.

Раздел 6. Расстояние между двумя прямыми
B1
C1
D1
A1
C
B
A
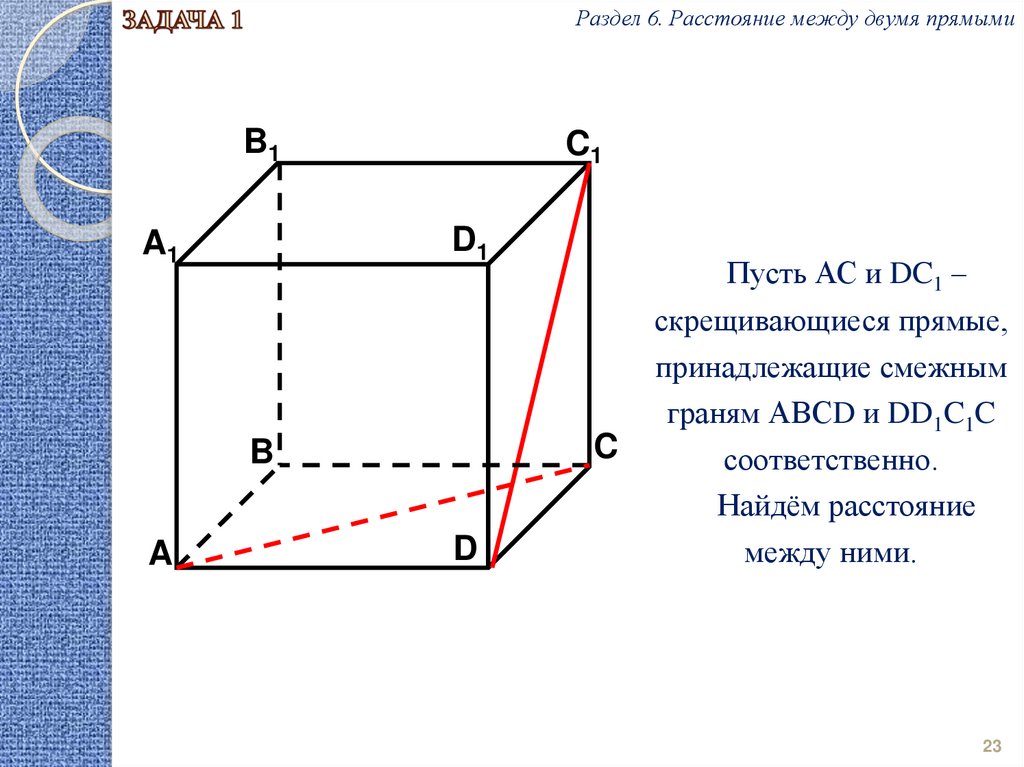
Пусть АС и DC1 –
D
скрещивающиеся прямые,
принадлежащие смежным
граням АВСD и DD1C1C
соответственно.
Найдём расстояние
между ними.
23

24.

Раздел 6. Расстояние между двумя прямыми
B1
A1
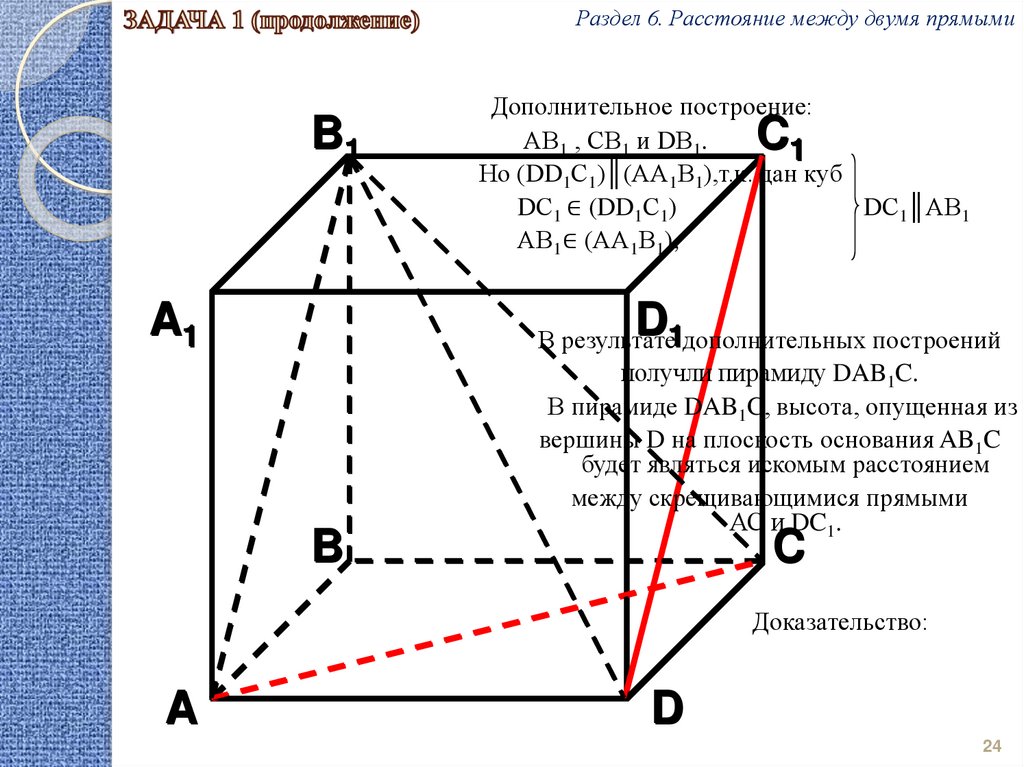
Дополнительное построение:
АВ1 , СВ1 и DВ1.
1
Но (DD1С1)║(АА1В1),т.к. дан куб
DС1 ∈ (DD1С1)
DС1║АВ1
АВ1∈ (АА1В1),
C
D
B
В результате1дополнительных построений
получли пирамиду DAB1C.
В пирамиде DAB1C, высота, опущенная из
вершины D на плоскость основания AB1C
будет являться искомым расстоянием
между скрещивающимися прямыми
АС и DC1.
C
Доказательство:
A
D
24

25.

Раздел 6. Расстояние между двумя прямыми
B1
A1
C1
D1
B
A
C
D
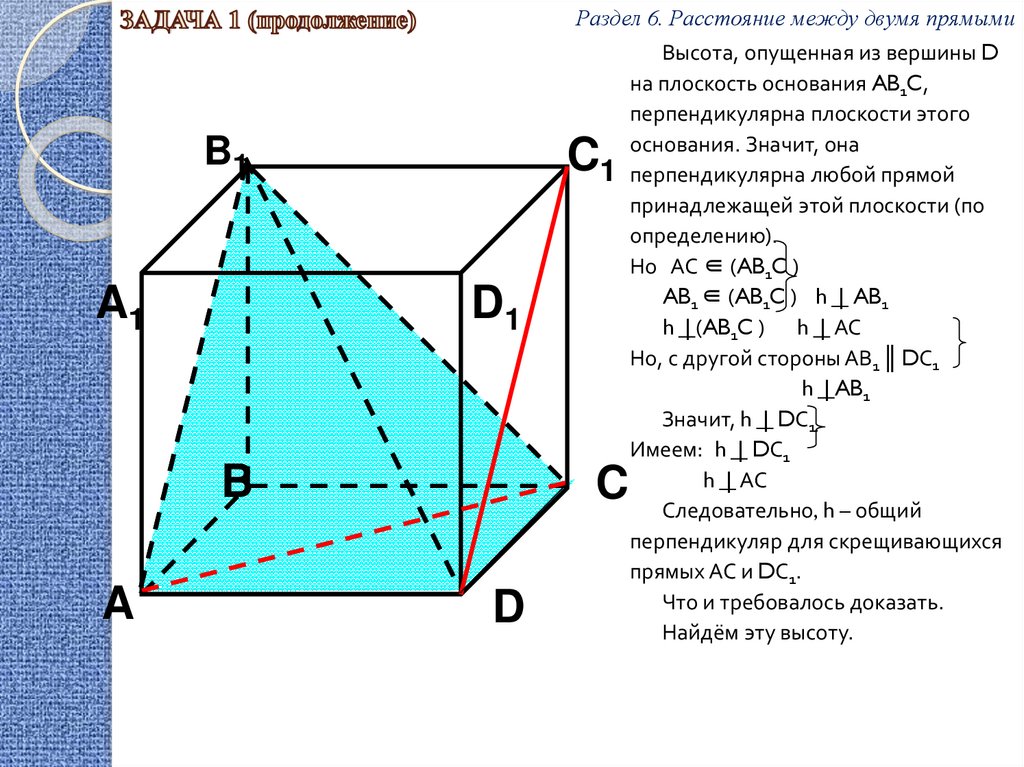
Высота, опущенная из вершины D
на плоскость основания AB1C,
перпендикулярна плоскости этого
основания. Значит, она
перпендикулярна любой прямой
принадлежащей этой плоскости (по
определению).
Но АС ∈ (AB1C )
AB1 ∈ (AB1C ) h | AB1
h | (AB1C ) h | АС
Но, с другой стороны АВ1 ║ DС1
h | AB1
Значит, h | DС1.
Имеем: h | DС1
h | АС
Следовательно, h – общий
перпендикуляр для скрещивающихся
прямых АС и DС1.
Что и требовалось доказать.
Найдём эту высоту.

26.

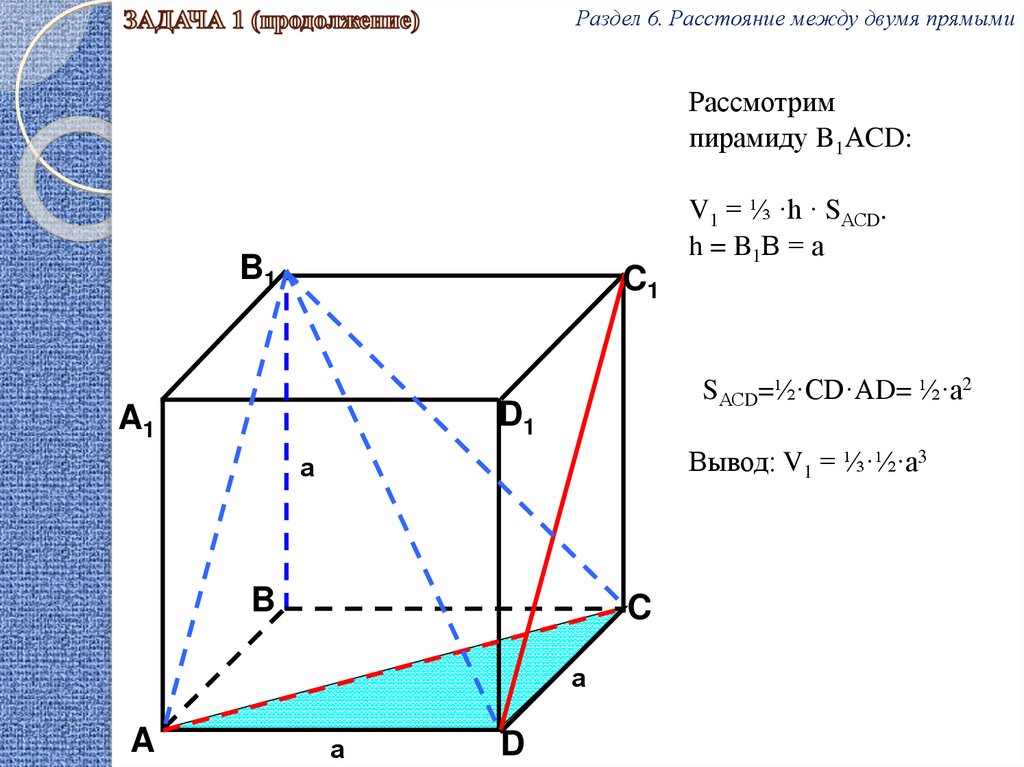
Раздел 6. Расстояние между двумя прямыми
Рассмотрим
пирамиду B1АCD:
B1
C1
SАСD=½·СD·АD= ½·а2
D1
A1
Вывод: V1 = ⅓·½·а3
а
B
C
а
A
V1 = ⅓ ·h · SАСD.
h = B1В = а
а
D

27.

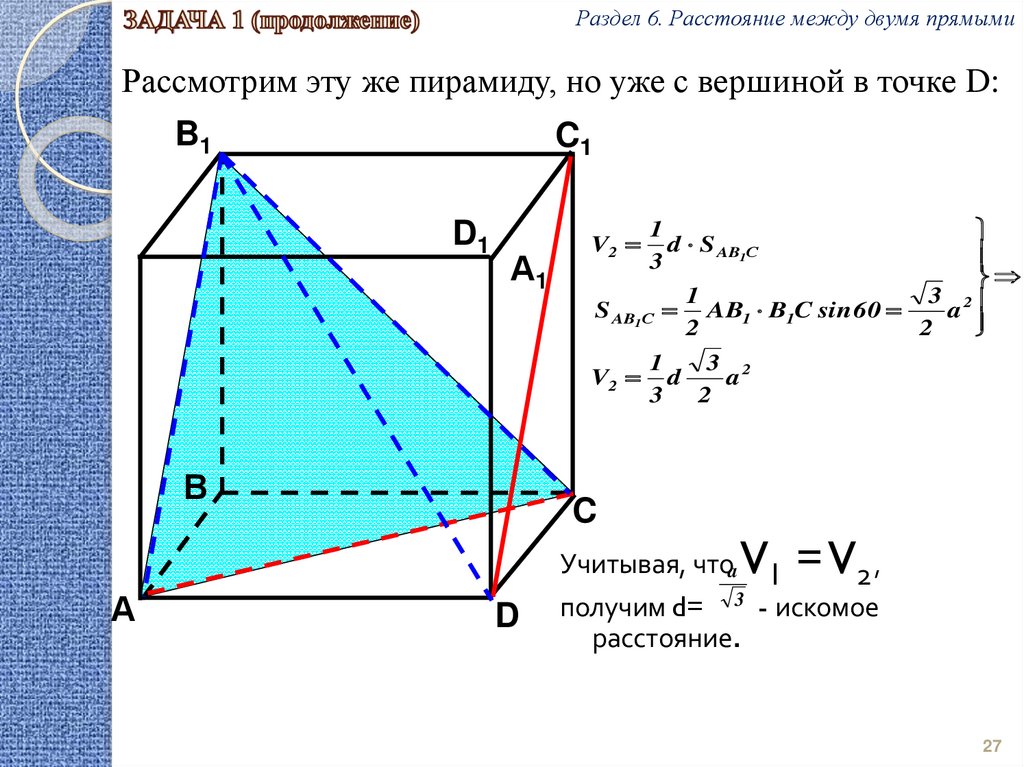
Раздел 6. Расстояние между двумя прямыми
Рассмотрим эту же пирамиду, но уже с вершиной в точке D:
B1
C1
D1
А1
1
d S AB1С
3
1
3 2
S AB1С AB1 B1C sin 60
a
2
2
V2
V2
В
А
1
3 2
d
a
3
2
C
Учитывая, чтоa V1
D
= V2 ,
получим d= 3 - искомое
расстояние.
27

28.

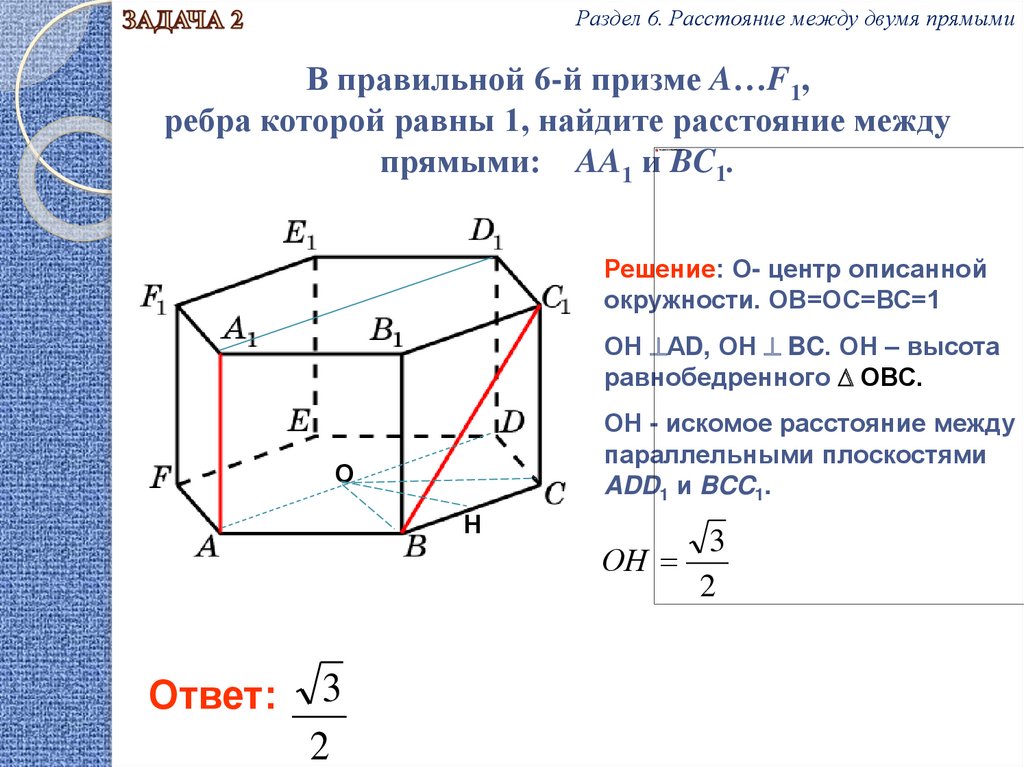
Раздел 6. Расстояние между двумя прямыми
В правильной 6-й призме A…F1,
ребра которой равны 1, найдите расстояние между
прямыми: AA1 и BC1.
Решение: О- центр описанной
окружности. ОВ=ОС=ВС=1
ОН АD, ОН BC. ОН – высота
равнобедренного ОВС.
ОН - искомое расстояние между
параллельными плоскостями
ADD1 и BCC1.
О
Н
Ответ:
3
2
3
ОН
2

29.

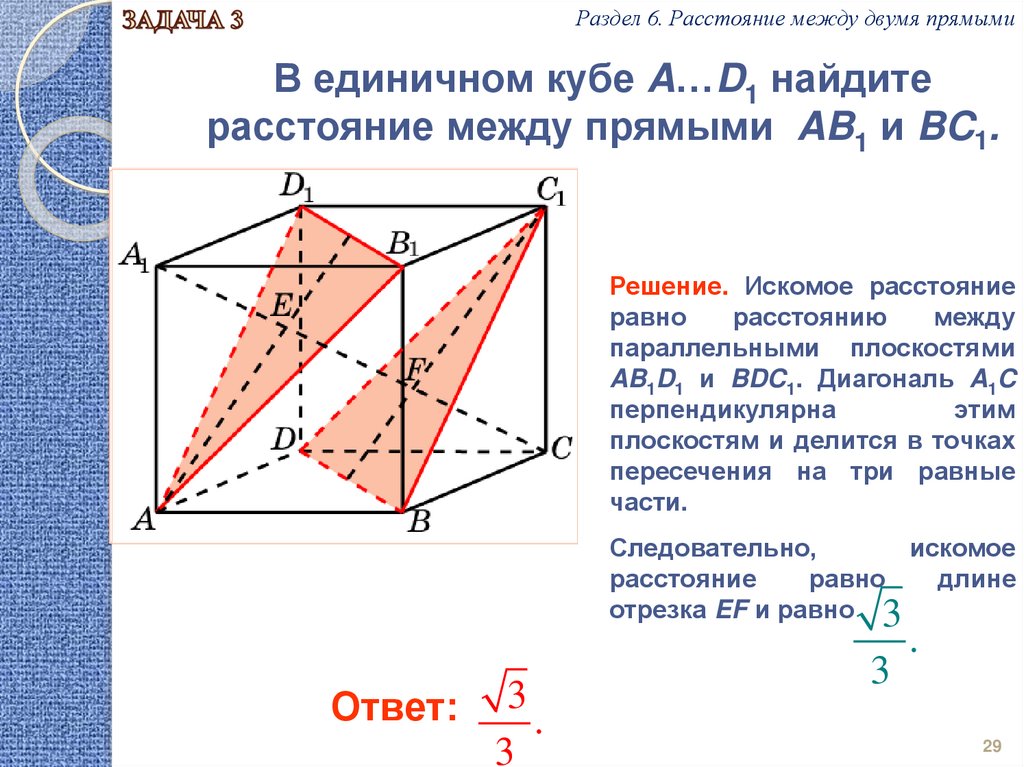
Раздел 6. Расстояние между двумя прямыми
В единичном кубе A…D1 найдите
расстояние между прямыми AB1 и BC1.
Решение. Искомое расстояние
равно
расстоянию
между
параллельными плоскостями
AB1D1 и BDC1. Диагональ A1C
перпендикулярна
этим
плоскостям и делится в точках
пересечения на три равные
части.
Следовательно,
искомое
расстояние
равно
длине
отрезка EF и равно 3
Ответ:
3
.
3
3
.
29