Magomadov_Zelimkhan_PresentationV1-1

1.

Quantum Key Distribution Integration for
Secure Microgrid Communication
Zelimkhan Magomadov — PhD Student, Year 2
Advisor: Asst. Prof. Oleg Khamisov
Program: Engineering Systems

2.

Motivation: Introduction into quantum
world
Quantum information is recorded in quantum bits (qubits):
Before the measurement:
0 1 2 2 1
After measurement: 0 or 1
They become a single system and the measurement of one immediately affects the
other.
As microgrids rely heavily on secure communication, QKD provides a physically
unbreakable way to protect control signals.
Fig.
1. “Quantum
analogy”
1
Fig. 2. Bits and Qbits

3.

Research Background and Problem Statement
The increasing
digitalization of
power grids has led
to a growing
reliance on secure
communication
systems.
Classic methods didn’t
work against quantum
threats.
An increase in the
frequency of attacks
on this sector.
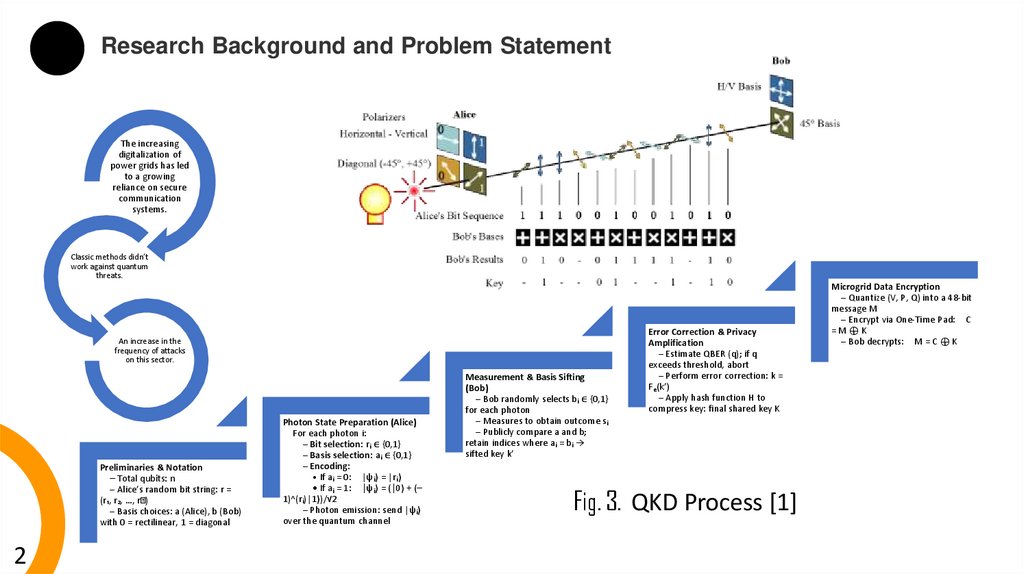
Preliminaries & Notation
– Total qubits: n
– Alice’s random bit string: r =
(r₁, r₂, …, rₙ)
– Basis choices: a (Alice), b (Bob)
with 0 = rectilinear, 1 = diagonal
2
Photon State Preparation (Alice)
For each photon i:
– Bit selection: rᵢ ∈ {0,1}
– Basis selection: aᵢ ∈ {0,1}
– Encoding:
• If aᵢ = 0: |ψᵢ⟩ = |rᵢ⟩
• If aᵢ = 1: |ψᵢ⟩ = (|0⟩ + (–
1)^(rᵢ)|1⟩)/√2
– Photon emission: send |ψᵢ⟩
over the quantum channel
Measurement & Basis Sifting
(Bob)
– Bob randomly selects bᵢ ∈ {0,1}
for each photon
– Measures to obtain outcome sᵢ
– Publicly compare a and b;
retain indices where aᵢ = bᵢ →
sifted key k′
Error Correction & Privacy
Amplification
– Estimate QBER (q); if q
exceeds threshold, abort
– Perform error correction: k =
Fₑ(k′)
– Apply hash function H to
compress key: final shared key K
Fig. 3. QKD Process [1]
Microgrid Data Encryption
– Quantize (V, P, Q) into a 48-bit
message M
– Encrypt via One-Time Pad: C
=M⊕K
– Bob decrypts: M = C ⊕ K

4.

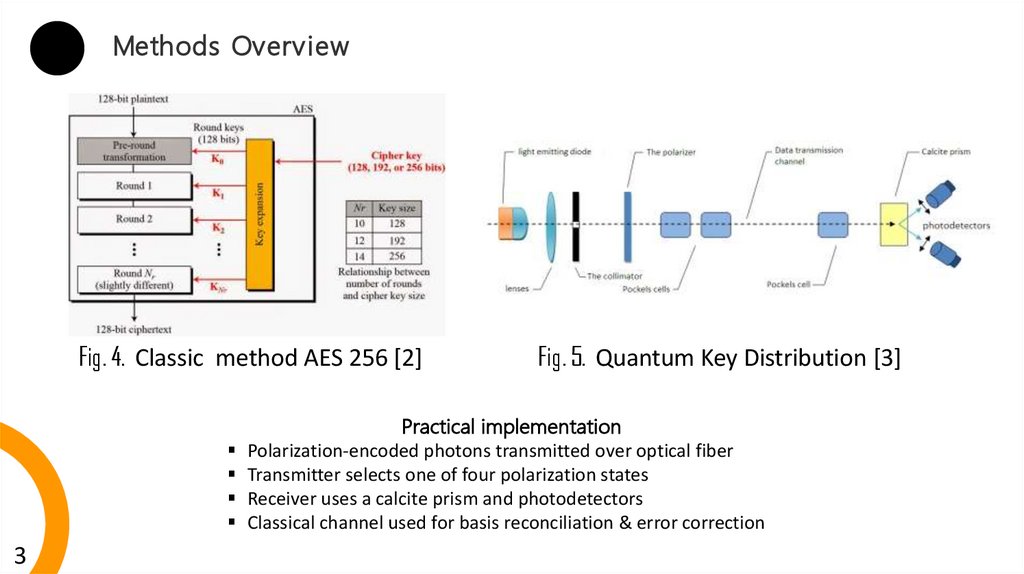
Methods Overview
Fig. 4. Classic method AES 256 [2]
Fig. 5. Quantum Key Distribution [3]
Practical implementation
Polarization-encoded photons transmitted over optical fiber
Transmitter selects one of four polarization states
Receiver uses a calcite prism and photodetectors
Classical channel used for basis reconciliation & error correction
3

5.

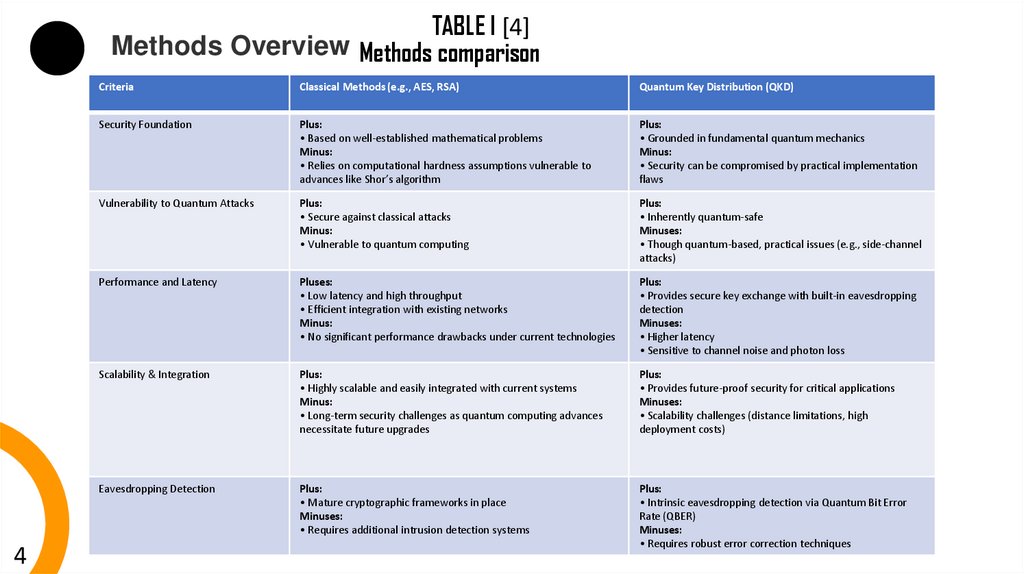
TABLE I [4]
Methods Overview Methods comparison
4
Criteria
Classical Methods (e.g., AES, RSA)
Quantum Key Distribution (QKD)
Security Foundation
Plus:
• Based on well-established mathematical problems
Minus:
• Relies on computational hardness assumptions vulnerable to
advances like Shor’s algorithm
Plus:
• Grounded in fundamental quantum mechanics
Minus:
• Security can be compromised by practical implementation
flaws
Vulnerability to Quantum Attacks
Plus:
• Secure against classical attacks
Minus:
• Vulnerable to quantum computing
Plus:
• Inherently quantum-safe
Minuses:
• Though quantum-based, practical issues (e.g., side-channel
attacks)
Performance and Latency
Pluses:
• Low latency and high throughput
• Efficient integration with existing networks
Minus:
• No significant performance drawbacks under current technologies
Plus:
• Provides secure key exchange with built-in eavesdropping
detection
Minuses:
• Higher latency
• Sensitive to channel noise and photon loss
Scalability & Integration
Plus:
• Highly scalable and easily integrated with current systems
Minus:
• Long-term security challenges as quantum computing advances
necessitate future upgrades
Plus:
• Provides future-proof security for critical applications
Minuses:
• Scalability challenges (distance limitations, high
deployment costs)
Eavesdropping Detection
Plus:
• Mature cryptographic frameworks in place
Minuses:
• Requires additional intrusion detection systems
Plus:
• Intrinsic eavesdropping detection via Quantum Bit Error
Rate (QBER)
Minuses:
• Requires robust error correction techniques

6.

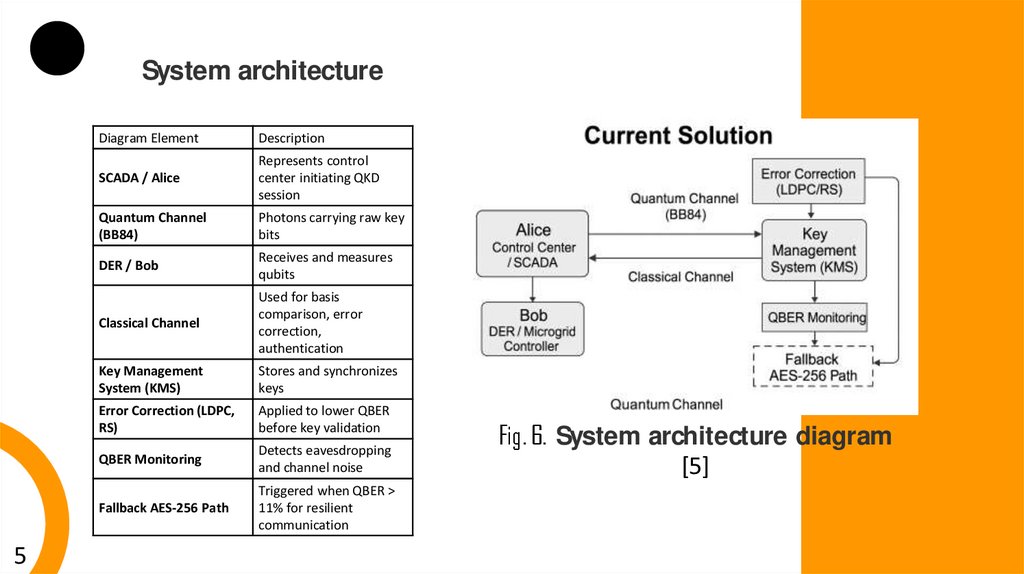
System architecture
5
Diagram Element
Description
SCADA / Alice
Represents control
center initiating QKD
session
Quantum Channel
(BB84)
Photons carrying raw key
bits
DER / Bob
Receives and measures
qubits
Classical Channel
Used for basis
comparison, error
correction,
authentication
Key Management
System (KMS)
Stores and synchronizes
keys
Error Correction (LDPC,
RS)
Applied to lower QBER
before key validation
QBER Monitoring
Detects eavesdropping
and channel noise
Fallback AES-256 Path
Triggered when QBER >
11% for resilient
communication
Fig. 6. System architecture diagram
[5]

7.

Conclusions
Conclusions:
•Security Enhancement:
• QKD provides a quantum-safe solution that enhances
microgrid communication by detecting intrusions via
QBER monitoring.
•Key Reliability:
• Error correction techniques (LDPC, Reed-Solomon) are
crucial for maintaining key integrity, making QKD
practical despite channel noise.
•Future Directions:
• Further optimization is needed to address latency and
integration challenges.
• Research will explore hybrid encryption models (QKDdistributed keys with AES for bulk data) and scalable
deployment strategies.
6
Fig. 7. Satellite-to-ground quantum key
distribution [6]

8.

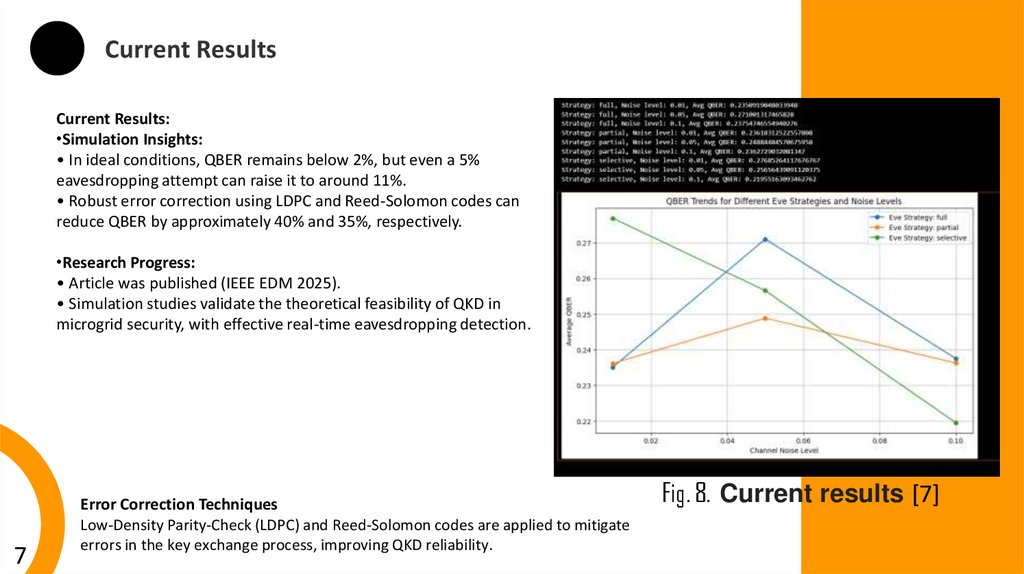
Current Results
Current Results:
•Simulation Insights:
• In ideal conditions, QBER remains below 2%, but even a 5%
eavesdropping attempt can raise it to around 11%.
• Robust error correction using LDPC and Reed-Solomon codes can
reduce QBER by approximately 40% and 35%, respectively.
•Research Progress:
• Article was published (IEEE EDM 2025).
• Simulation studies validate the theoretical feasibility of QKD in
microgrid security, with effective real-time eavesdropping detection.
7
Error Correction Techniques
Low-Density Parity-Check (LDPC) and Reed-Solomon codes are applied to mitigate
errors in the key exchange process, improving QKD reliability.
Fig. 8. Current results [7]

9.

1
2
3
8
Strengths:
• QKD enables quantum-safe communication
and provides measurable intrusion
detection via QBER.
• Integration with microgrid control layers
(SCADA, EMS) is feasible through fiberbased architectures.
Limitations:
• Real-world QKD suffers from photon loss,
noise, and limited key generation rates.
• Simulation assumptions do not fully
capture environmental variability.
Open Questions:
• How scalable is QKD for large multi-node
microgrids?
• What hybrid schemes (QKD + AES) provide
the optimal trade-off between security and
latency?
Discussion

10.

Related Publications
Supporting This Research
Published:
• M. Magomadov and O. O. Khamisov, “Quantum Key Distribution in Power System
Communication,” IEEE EDM, 2025.
(Introduces the initial microgrid-QKD integration model used in this proposal.)
In Preparation:
• Manuscript on advanced QKD error correction and hybrid QKD–AES encryption for
resilient energy systems.
(Expands the methods section of this thesis.)
9

11.

R eferences
10
[1] C. H. Bennett and G. Brassard, “Quantum cryptography: Public key distribution
and coin tossing,” in Proc. IEEE Int. Conf. Computers, Systems, and Signal Processing,
Bangalore, India, 1984, pp. 175–179.
[2] N. Gisin, G. Ribordy, W. Tittel, and H. Zbinden, “Quantum cryptography,” Rev.
Mod. Phys., vol. 74, no. 1, pp. 145–195, 2002.
[3] V. Scarani, H. Bechmann-Pasquinucci, N. J. Cerf, M. Dušek, N. Lütkenhaus, and M.
Peev, “The security of practical quantum key distribution,” Rev. Mod. Phys., vol. 81,
pp. 1301–1350, 2009.
[4] T. Sasaki, Y. Yamamoto, and M. Koashi, “Practical quantum key distribution
protocol without monitoring signal disturbance,” Nature, vol. 509, pp. 475–478,
2014.
[5] Z. Magomadov and O. O. Khamisov, “Quantum key distribution in power system
communication,” in Proc. IEEE EDM, Altai, Russia, 2025, pp. 1180–1185, doi:
10.1109/EDM65517.2025.11096656.
[6] S. Wang, L. Jiang, Y. Guan, and H. Zhang, “QKD integration in smart grid
communication networks,” IEEE Trans. Smart Grid, vol. 12, no. 4, pp. 3101–3115,
2021.
[7] R. Kumar and P. Singh, “Error correction techniques in quantum key distribution,”
IEEE Access, vol. 9, pp. 115200–115218, 2021.

12.

Thx for attention