МО_Лекция 13_Геометрический способ решения ЗНЛП

1. Методы оптимизации

МЕТОДЫ
ОПТИМИЗАЦИИ
Задачи нелинейного
программирования

2.

Общая постановка задачи нелинейного
программирования
f ( x1 , x2 , ..., xn ) max(min)
g i ( x1 , x2 , ..., xn ) bi , i 1, 2,..., k ,
g i ( x1 , x2 ,..., xn ) bi , i k 1, k 2, ...., m
f ( x1 ,..., xn ) max(min)
g ( x ,..., x ) b (i 1, m)
i
1
n
- общая задача нелинейного программирования
хотя бы одна функция НЕЛИНЕЙНА!
- задача классической оптимизации
i
Отличия от ЗЛП:
1. ОДЗ не обязательно выпуклая.
2. Экстремум не обязан находится
на границе ОДЗ.
Если в ЗНЛП присутствуют ограничения
на переменные (дополнительные условия),
то такую задачу называют задачей условной
оптимизации.
При отсутствии ограничений имеет
место задача безусловной оптимизации.

3.

Свойства ЗНЛП
1. Множество допустимых планов D может иметь очень сложную структуру
(например, быть невыпуклым или несвязным).
2. Глобальный максимум (минимум) может достигаться как внутри множества D,
так и на его границах (где он, вообще говоря, будет не совпадать ни с одним из
локальных экстремумов).
3.
Целевая функция f может быть недифференцируемой, что затрудняет
применение классических методов математического анализа.

4.

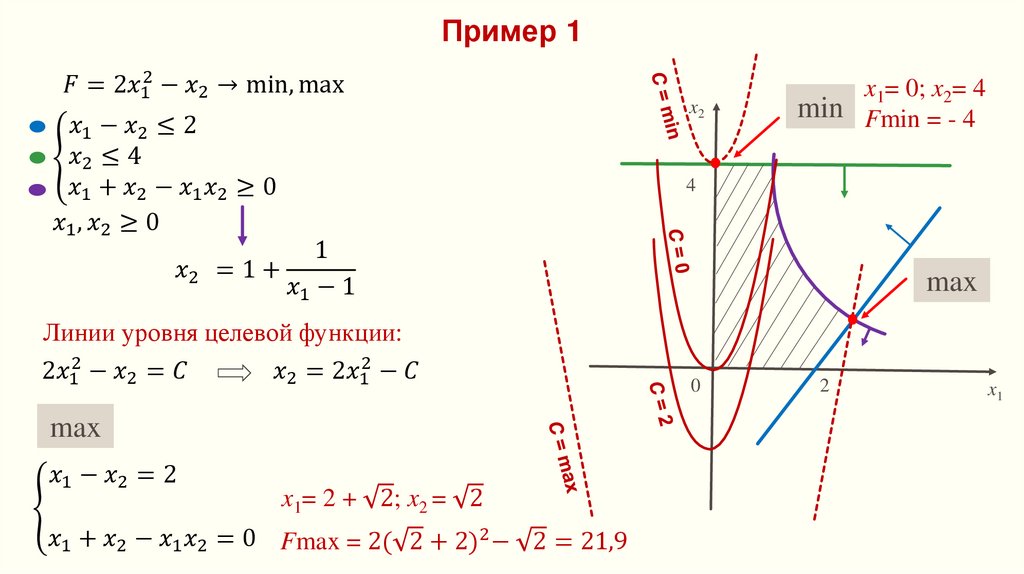
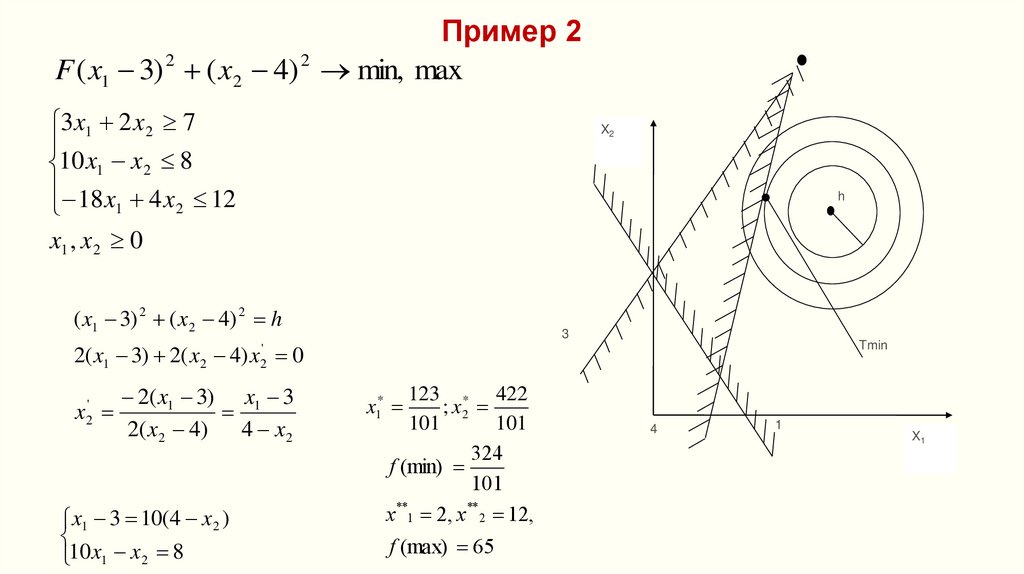
Геометрическая интерпретация ЗНЛП
Если определена область допустимых решений (ОДР), то нахождение решения задачи сводится
к определению такой точки этой области, через которую проходит гиперповерхность наивысшего
(наинизшего) уровня:
f ( x1 , x2 , ..., xn ) h.
Указанная точка может находиться как на границе ОДР, так и внутри нее.
1.
Этапы решения:
Находят ОДР задачи, определяемую соотношениями системы ограничений (если она пуста, то
задача не имеет решения).
2.
Строят гиперповерхность f ( x1 , x2 , ..., xn ) h.
3.
Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают
неразрешимость задачи из-за неограниченности целевой функции сверху (снизу) на множестве
допустимых решений.
4.
Находят точку ОДР, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и
определяют в ней значение целевой функции.
5.
Уместно отметить, что данную задачу целесообразно решать в двумерном (в крайнем случае,
трёхмерном) пространстве.

5.

Пример 1