Ветвящиеся_временные_логики_Иванов_Н_А_ПО1_22

1.

Ветвящиеся временные
логики: Путешествие во
времени и возможностях

2.

Временная логика: что это и зачем?
Временная логика — это раздел математической логики, который
изучает утверждения, учитывающие изменение истинности
высказываний во времени. Она позволяет описывать и рассуждать о
последовательностях событий и состояниях систем, которые
эволюционируют с течением времени.
Логика, учитывающая изменение истинности высказываний во
времени.
Основана на работах Артура Прайора (1950-е), развита в
информатике Амиром Пнуэли.
Позволяет формализовать утверждения типа «будет ли когдалибо…», «всегда ли…», «пока не…».

3.

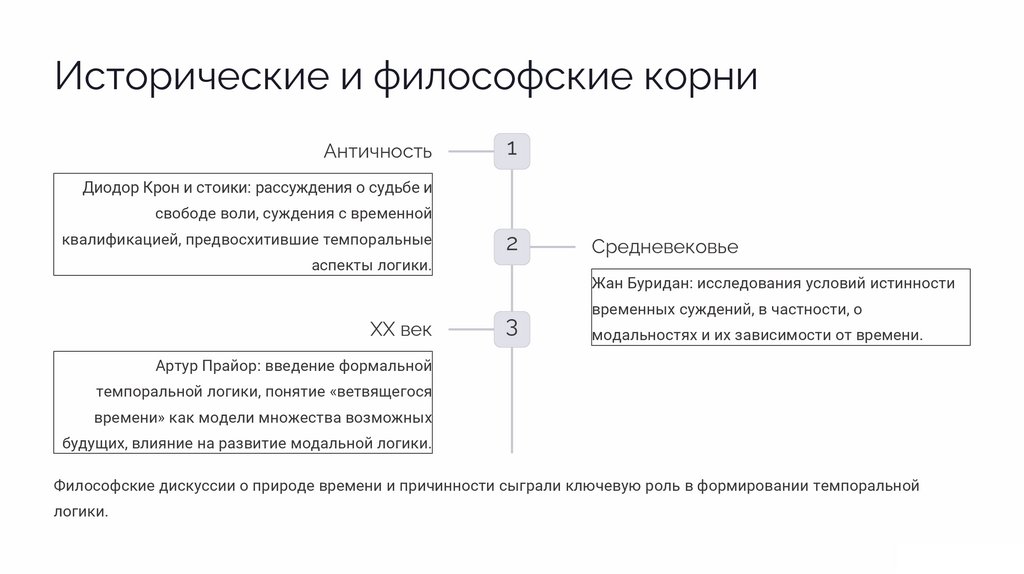
Исторические и философские корни
Античность
1
Диодор Крон и стоики: рассуждения о судьбе и
свободе воли, суждения с временной
квалификацией, предвосхитившие темпоральные
2
аспекты логики.
XX век
Средневековье
Жан Буридан: исследования условий истинности
3
временных суждений, в частности, о
модальностях и их зависимости от времени.
Артур Прайор: введение формальной
темпоральной логики, понятие «ветвящегося
времени» как модели множества возможных
будущих, влияние на развитие модальной логики.
Философские дискуссии о природе времени и причинности сыграли ключевую роль в формировании темпоральной
логики.

4.

Линейное vs ветвящееся время
Линейная временная логика (LTL)
Представляет время как одну единственную, неизменную
последовательность событий, где каждое состояние имеет только
одно будущее.
Применение: системы с детерминированным поведением.
Ветвящаяся временная логика (CTL, CTL*)
Моделирует время как дерево возможных вариантов развития, где из
каждого состояния может вести множество путей в будущее.
Применение: недетерминированные системы, параллельные
вычисления.
Ветвление отражает неопределённость и альтернативные сценарии развития, что
критически важно для анализа сложных систем.

5.

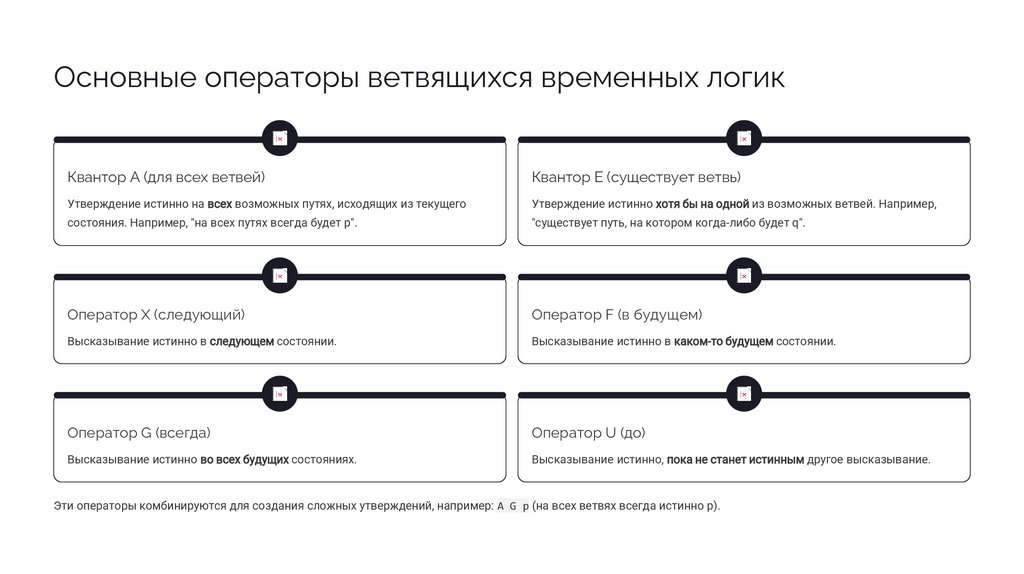
Основные операторы ветвящихся временных логик
Квантор A (для всех ветвей)
Квантор E (существует ветвь)
Утверждение истинно на всех возможных путях, исходящих из текущего
Утверждение истинно хотя бы на одной из возможных ветвей. Например,
состояния. Например, "на всех путях всегда будет p".
"существует путь, на котором когда-либо будет q".
Оператор X (следующий)
Оператор F (в будущем)
Высказывание истинно в следующем состоянии.
Высказывание истинно в каком-то будущем состоянии.
Оператор G (всегда)
Оператор U (до)
Высказывание истинно во всех будущих состояниях.
Высказывание истинно, пока не станет истинным другое высказывание.
Эти операторы комбинируются для создания сложных утверждений, например: A G p (на всех ветвях всегда истинно p).

6.

Формальные системы и модели
Деревья состояний
Верификация систем
Модели в ветвящихся временных
Автоматы Бюхи: используются для
логиках часто представляются в виде
представления бесконечных
деревьев состояний, где узлы — это
последовательностей состояний,
состояния системы, а рёбра —
критичных для проверки свойств
возможные переходы между ними.
живых систем.
Эти деревья могут быть как
конечными, так и бесконечными.
Модели: деревья состояний с
переходами, где каждое состояние
может иметь множество
последующих состояний.
Формулы CTL и CTL*: определяют
строгий синтаксис и семантику
для выражения темпоральных
свойств.
Алгоритмы Model Checking:
автоматизированные методы для
проверки, удовлетворяет ли
система заданным темпоральным
свойствам. Они просматривают
все возможные пути в модели.

7.

Применения ветвящихся временных логик
Формальная
верификация
Спецификация
реактивных
систем
Искусственный
интеллект и
планирование
доказательства
Применяются для
Анализ и синтез
корректности и
описания и проверки
планов действий для
безопасности
поведения систем,
интеллектуальных
программного
которые постоянно
агентов, позволяя им
обеспечения,
взаимодействуют со
выбирать
микропроцессоров и
своей средой,
оптимальные
цифровых схем,
например, протоколов
стратегии с учётом
гарантируя отсутствие
связи, операционных
множества
ошибок и выполнение
систем и систем
возможных будущих
критически важных
реального времени.
сценариев.
Использование для
требований.

8.

Научные разработки и
современные тренды
Эвристические
алгоритмы
Комбинации с другими
логиками
Разработка оптимизированных
Интеграция с темпоральной
алгоритмов для ускоренной
логикой действий (TLA+) для
проверки темпоральных свойств,
более полного описания и
например, на базе исследований
верификации распределённых и
МИНОТ и РГГУ, что повышает
параллельных систем.
эффективность model checking.
Расширенные темпоральные логики
Развитие интервальной и метрической темпоральных логик для более
точного описания временных интервалов и длительности событий, что
позволяет работать с количественными аспектами времени.

9.

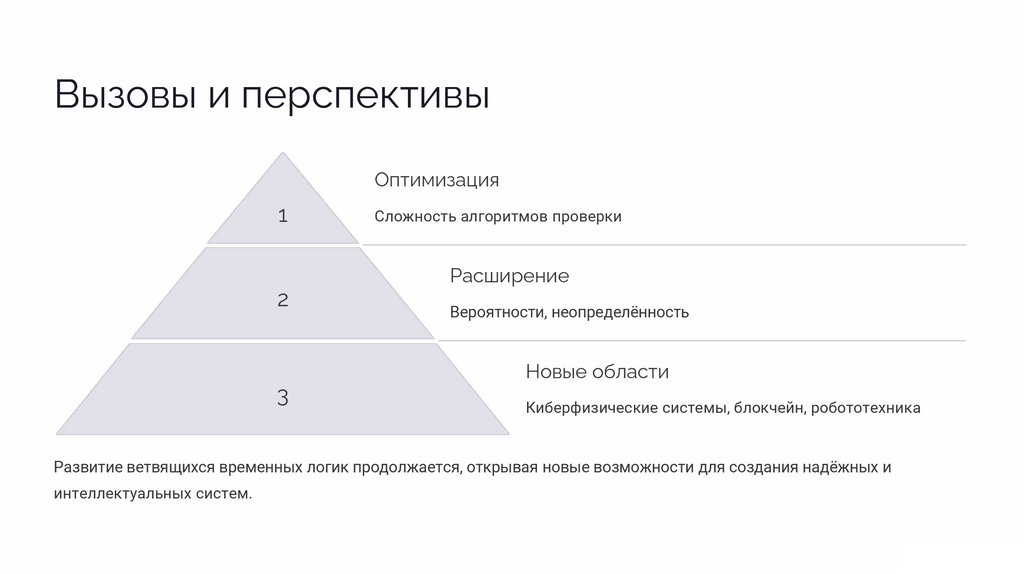
Вызовы и перспективы
Оптимизация
1
2
3
Сложность алгоритмов проверки
Расширение
Вероятности, неопределённость
Новые области
Киберфизические системы, блокчейн, робототехника
Развитие ветвящихся временных логик продолжается, открывая новые возможности для создания надёжных и
интеллектуальных систем.

10.

Заключение: Ветвящиеся временные логики — ключ
к пониманию времени и возможностей
Ветвящиеся временные логики представляют собой мощный аналитический инструмент, позволяющий не только формализовать и
анализировать сложные временные сценарии, но и предсказывать поведение систем в условиях неопределённости. Они
обеспечивают основу для:
Повышения надёжности и безопасности систем: от программного обеспечения до сложных киберфизических комплексов.
Открытия новых горизонтов: в логике, информатике и философии времени, углубляя наше понимание взаимосвязи между
временем, выбором и последствиями.