gases_chapter_6

1.

GENERAL CHEMISTRY
Principles and Modern Applications
PETRUCCI
HERRING
Gases
MADURA
TENTH EDITION
BISSONNETTE
6

2. Gases

CONTENTS
6- 1
Properties of Gases: Gas Pressure
6- 2
The Simple Gas Laws
6- 3
Combining the Gas Laws: The Ideal Gas
Equation and The General Gas
Equation
6- 4
Applications of the Ideal Gas Equation
6- 5
Gases in Chemical Reactions
6- 6
Mixtures of Gases
6- 7
Kinetic—Molecular Theory of Gases
6- 8
Gas Properties Relating to the Kinetic—
Molecular Theory
6- 9
Nonideal (Real) Gases

3. The gaseous state of three halogens (group 7)

The greenish yellow gas is the brownish red gas is above
a small pool of liquid bromine; the violet gas is in
contact with grayish-black solid iodine. Most other
common gases, such as CO2, O2, N2 and H2 are colorless.

4. The Concept of Pressure

Force
Force (N) = g (m/s2) x m (kg)
Pressure
P (Pa) =
The Concept of Pressure
Force (N)
Area (m2)

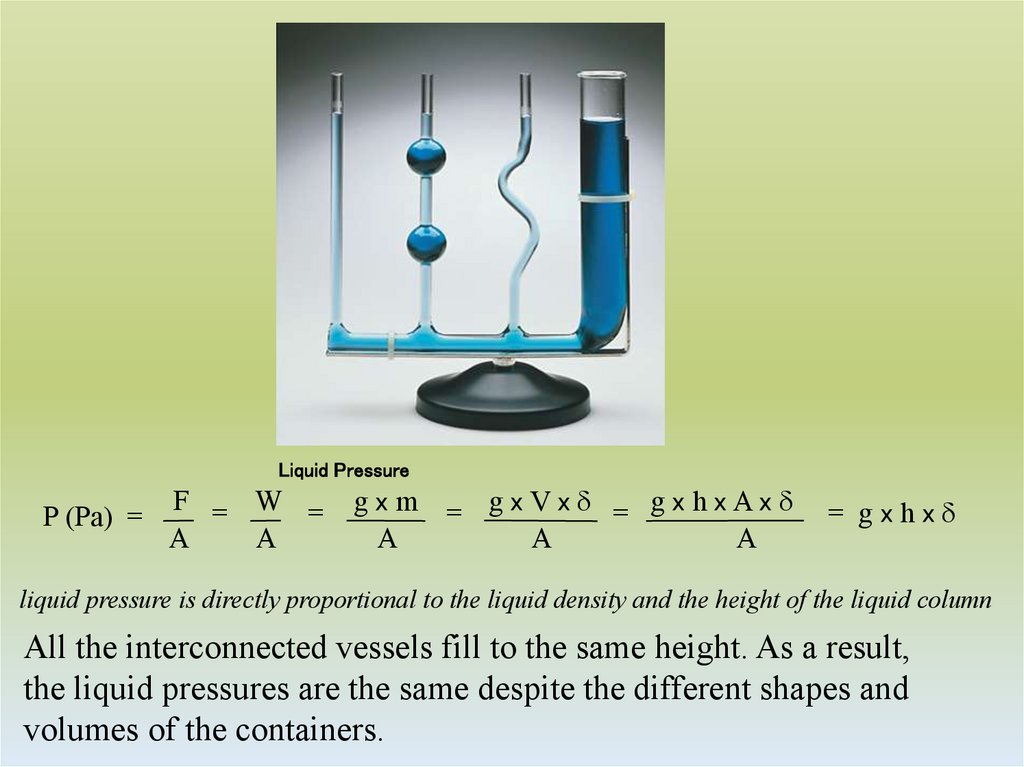
5. Liquid Pressure

P (Pa) =
F = W =
A
A
gx m = gxVx d = gx hxAxd
A
A
A
= gxhxd
liquid pressure is directly proportional to the liquid density and the height of the liquid column
All the interconnected vessels fill to the same height. As a result,
the liquid pressures are the same despite the different shapes and
volumes of the containers.

6.

Standard Atmospheric Pressure 1.00 atm, 760 mm Hg
Arrows represent the pressure exerted by the atmosphere.
(a)The liquid mercury levels are equal inside and outside the open-end
tube.
(b) A column of mercury 760 mm high is maintained in the closed-end
tube, regardless of the overall height of the tube
(c) as long as it exceeds 760 mm.
(d) A column of mercury fills a closed-end tube that is shorter than 760
mm. In the closed-end tubes in (b) and (c), the region above the mercury
column is devoid of air and contains only a trace of mercury vapor.

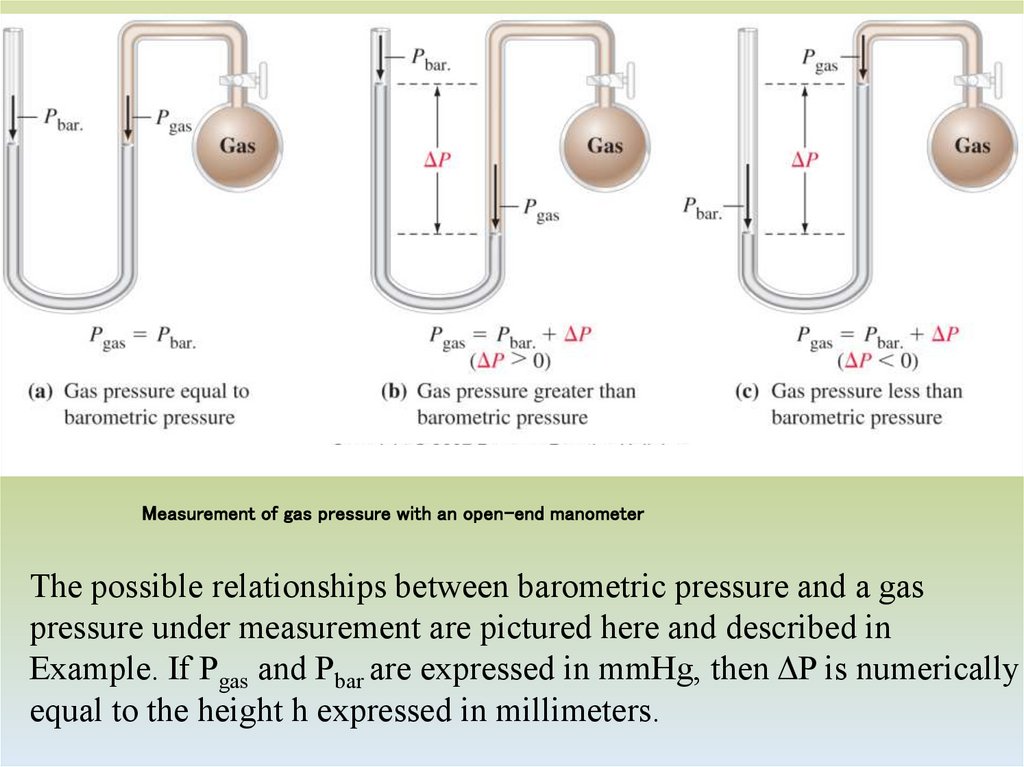
7. Measurement of gas pressure with an open-end manometer

The possible relationships between barometric pressure and a gas
pressure under measurement are pictured here and described in
Example. If Pgas and Pbar are expressed in mmHg, then ΔP is numerically
equal to the height h expressed in millimeters.

8.

Examples:
1. What is the gas pressure Pgas if the conditions in figure c are those.
The manometer is filled with liquid mercury (d: 13.6 g/cm3)
barometric pressure is 748.2 mmHg and the differences in mercury
levels is 8.6 mmHg
2. The manometer is filed with liquid glycerol (d: 1.26 g/cm3) instead
of the mercury What would be the difference in the two levels of the
liquid for ex 1?

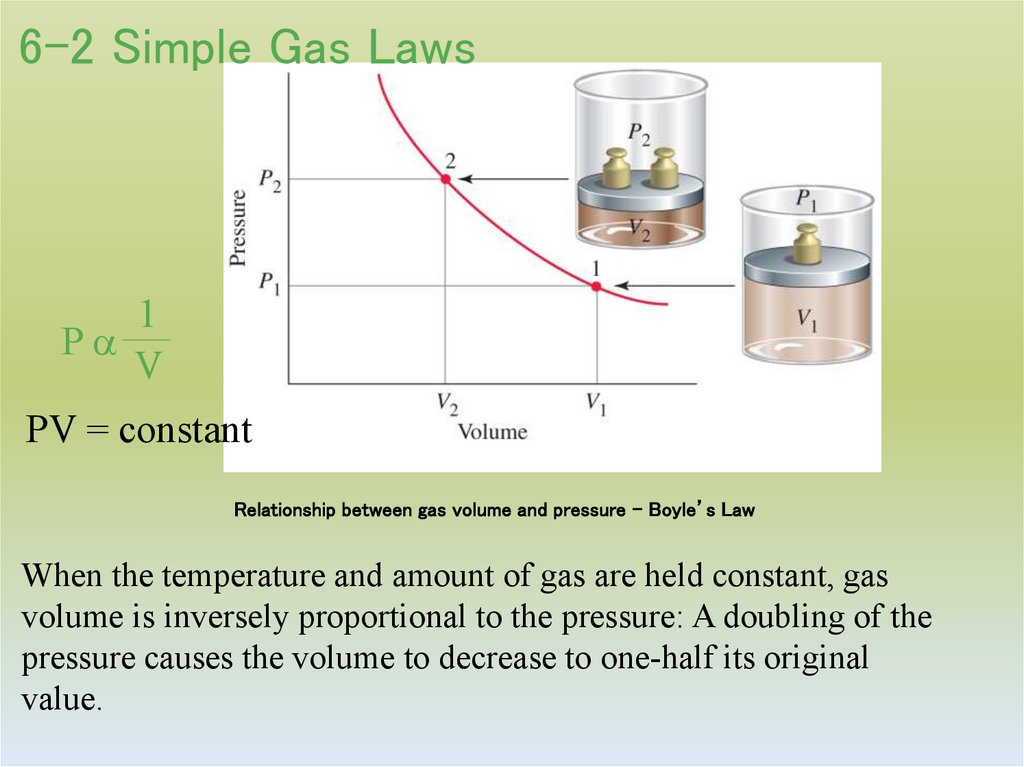
9. Relationship between gas volume and pressure – Boyle’s Law

6-2 Simple Gas Laws
1
Pa
V
PV = constant
Relationship between gas volume and pressure – Boyle’s Law
When the temperature and amount of gas are held constant, gas
volume is inversely proportional to the pressure: A doubling of the
pressure causes the volume to decrease to one-half its original
value.

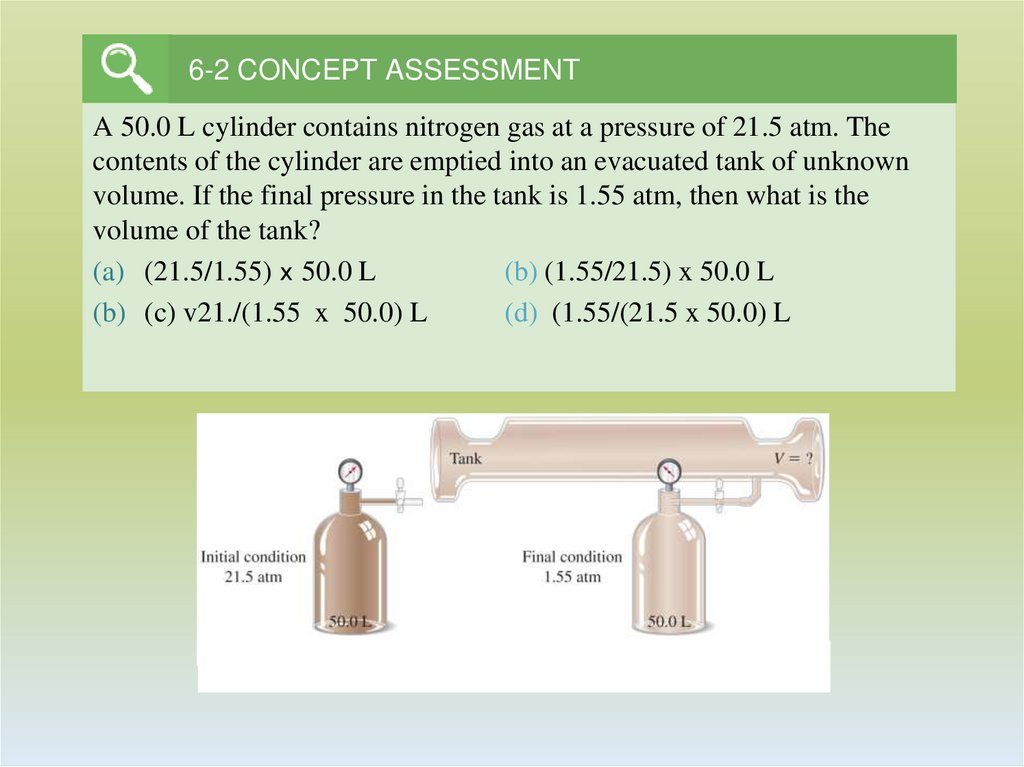
10. 6-2 CONCEPT ASSESSMENT

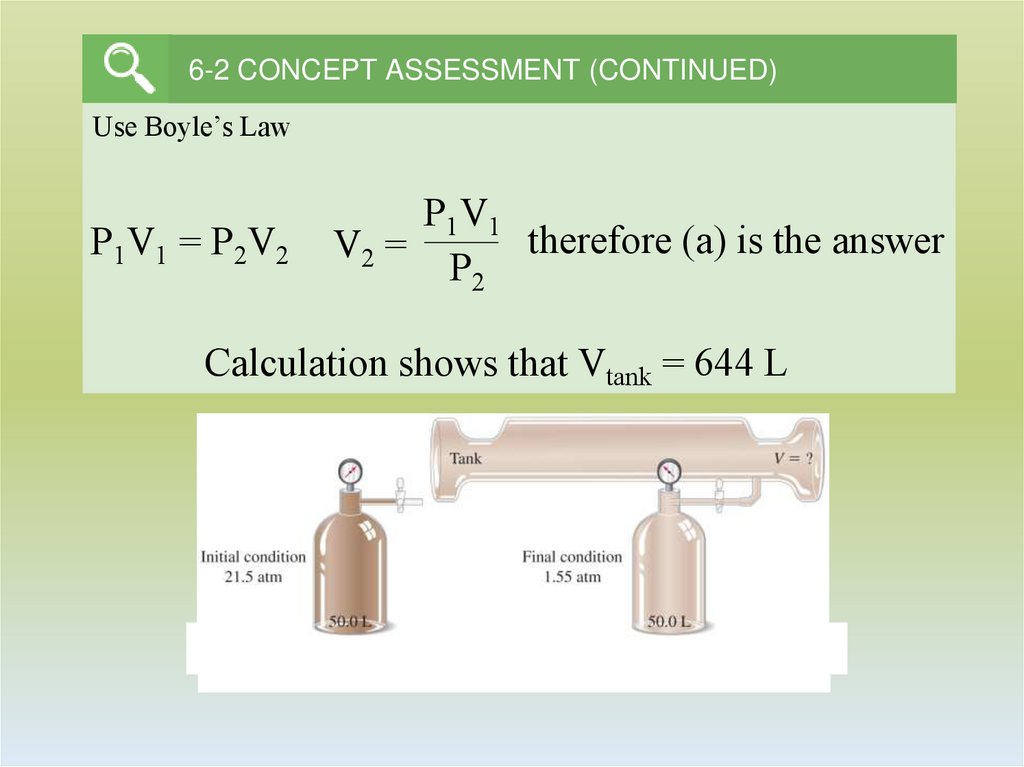
A 50.0 L cylinder contains nitrogen gas at a pressure of 21.5 atm. The
contents of the cylinder are emptied into an evacuated tank of unknown
volume. If the final pressure in the tank is 1.55 atm, then what is the
volume of the tank?
(a) (21.5/1.55) x 50.0 L
(b) (1.55/21.5) x 50.0 L
(b) (c) v21./(1.55 x 50.0) L
(d) (1.55/(21.5 x 50.0) L

11. 6-2 CONCEPT ASSESSMENT (CONTINUED)

Use Boyle’s Law
P1V1 = P2V2
P1V1
therefore (a) is the answer
V2 =
P2
Calculation shows that Vtank = 644 L

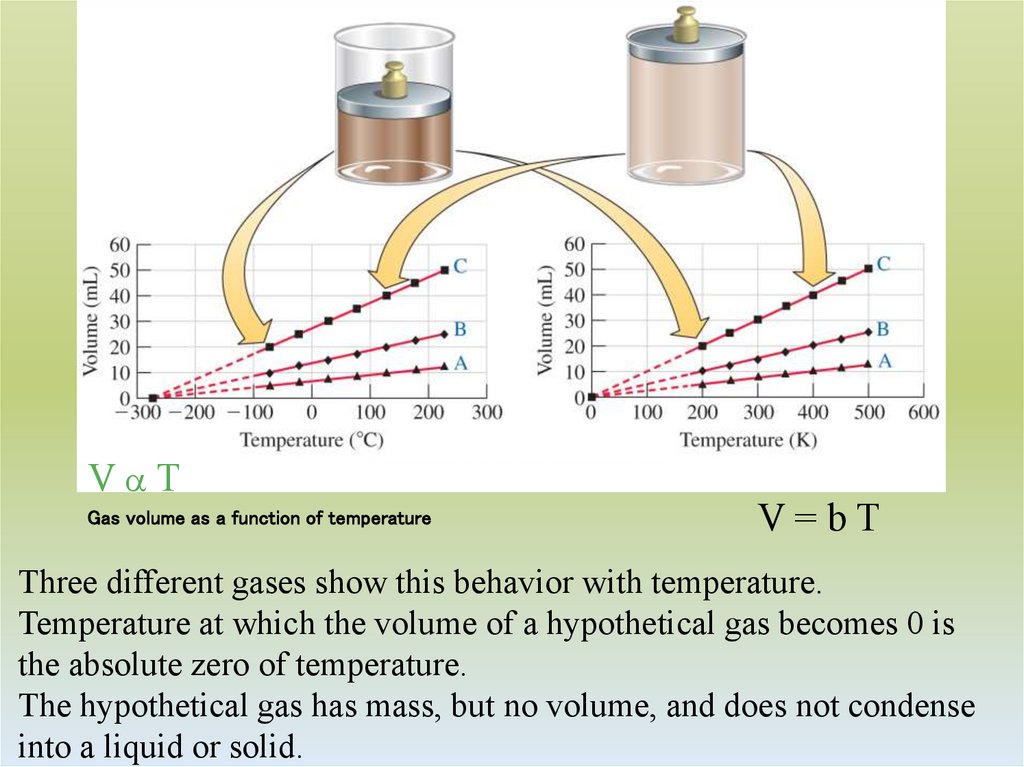
12. Gas volume as a function of temperature

VaT
Gas volume as a function of temperature
V=bT
Three different gases show this behavior with temperature.
Temperature at which the volume of a hypothetical gas becomes 0 is
the absolute zero of temperature.
The hypothetical gas has mass, but no volume, and does not condense
into a liquid or solid.

13.

Examples
1. A balloon is inflated to a volume of 2.5 L in a warm living
room (250C) That it is taken outside on a very cold winter
day (-240C) Assume that quality of air in the balloon and its
pressure both remain constant. What will be the volume of
the balloon when it is outdoors?

14. Standard Temperature and Pressure

Gas properties depend on conditions.
IUPAC defines standard conditions of temperature
and pressure (STP).
P = 1 Bar = 105 Pa
T = 0°C = 273.15 K
Note that the text does not use the older standard of 1 atm. 1 Bar
is the IUPAC definition of Standard conditions of temperature and
pressure.

15.

Examples
1. Which will have the greater volume when the gases are
compared at STP: a. 1.2 L N2(g) at 25 0C and 748 mmHg b.
1.25 L O2(g) at STP?

16. Avogadro’s Law

Gay-Lussac 1808
Small volumes of gases react in the ratio of small whole
numbers.
Avogadro 1811
At a fixed temperature and pressure, the volume of a
gas is directly proportional to the amount of gas.

17. Molar volume of a gas visualized

At fixed T and P
V n
or
V=cn
At STP
Molar volume of a gas visualized
1 mol gas = 22.4 L gas
Wooden cube is 28.2 cm on edge and has approximately the
same volume as one mole of gas at 1 atm and 0°C.
Basketball = 7.5 L, Soccer ball = 6.0 L and Football = 4.4 L

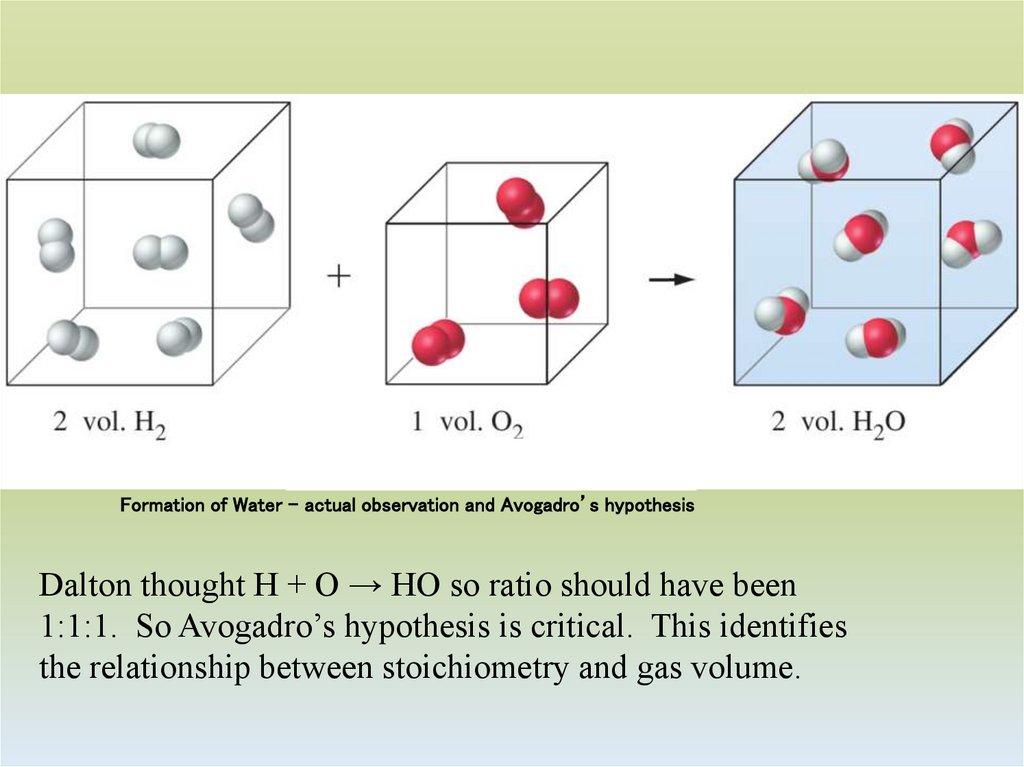
18. Formation of Water – actual observation and Avogadro’s hypothesis

Dalton thought H + O → HO so ratio should have been
1:1:1. So Avogadro’s hypothesis is critical. This identifies
the relationship between stoichiometry and gas volume.

19.

Examples
1. What is the mass of 1L of cyclopropane gas (C3H6) when
measured at STP
2. 128 g piece of solid CO2 sublimes into CO2. What is the
volume of this gas at STP, in liters?

20. 6-3 Combining the Gas Laws: The Ideal Gas Equation and the General Gas Equation

Boyle’s law
V 1/P
Charles’s law
V T
Avogadro’s law
V n
nT
V
P
Any gas whose behavior conforms to the ideal gas equation is
called an ideal or perfect gas.
R is the gas constant. Substitute and calculate.

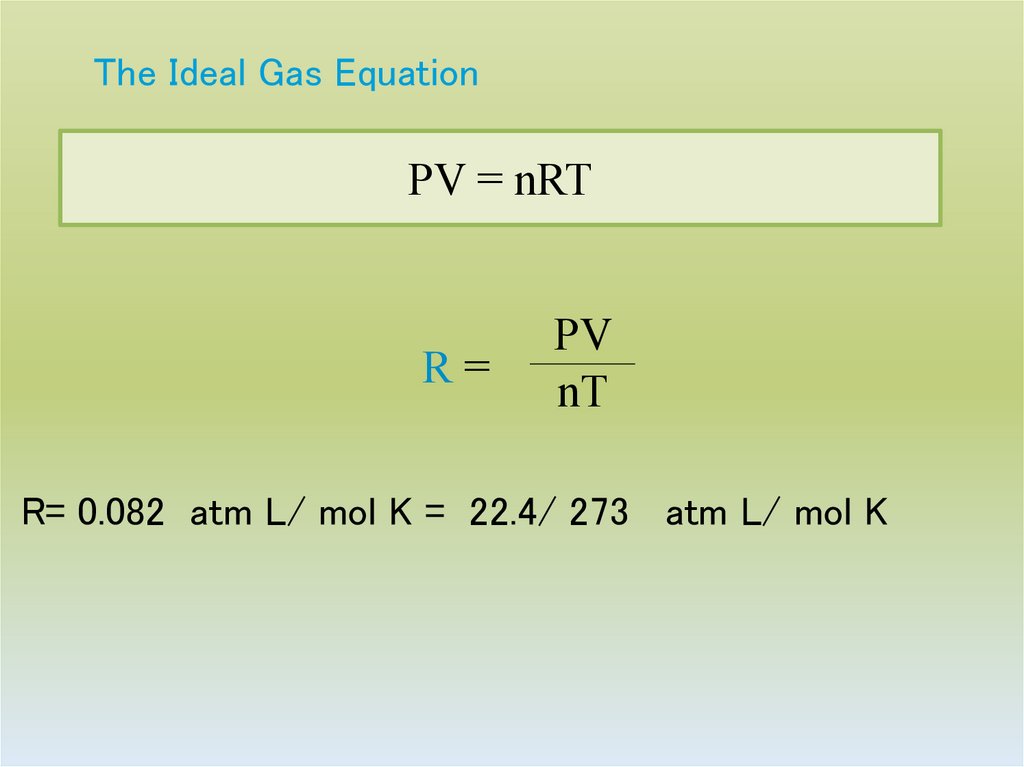
21. The Ideal Gas Equation

PV = nRT
R=
PV
nT
R= 0.082 atm L/ mol K = 22.4/ 273 atm L/ mol K

22.

Examples
1. What is the volume occupied by 13.7 g Cl2(g) at 45 0C and
745 mmHg?
2. What is the volume occupied by 20.2 g NH3 at -250Cand
752mmHg?
3. How many moles of He(g) are in a 5 L storage tank filled
with He at 10.5 atm pressure and 300C?

23. Applying the ideal gas equation

Molar Mass Determination
PV = mRT / Ma
Examples
1.
A glass vessel weighs 40.1305 g when clean, dry and evacuated:
138.2410g when field with water at 25 0C ( density of water = 0.9970
g/ml) and 40.2959 g when field with propylene gas st 740.3 mmHg and
24 0C. What is the molar mass of propylene?
2.
1.27 g sample of an oxide of nitrogen occupies a volume of 1.07 L at
25 0C and 737 mmHg. Which oxide is it?

24. Gas Densities

d= Ma P/ RT
Example
What is the density of O2 at 298 K and 0.987 atm?
Gas densities differ from solid and liquid densities in two important ways.
1.
Gas densities depend strongly on pressure and temperature . Densities of
liquid and solid also depend somewhat on temperature, but they depend far
less on pressure.
2.
The density of gas is directly proportional to its molar mass. No simple
relationship exists between density and molar mass for liquids and solids.

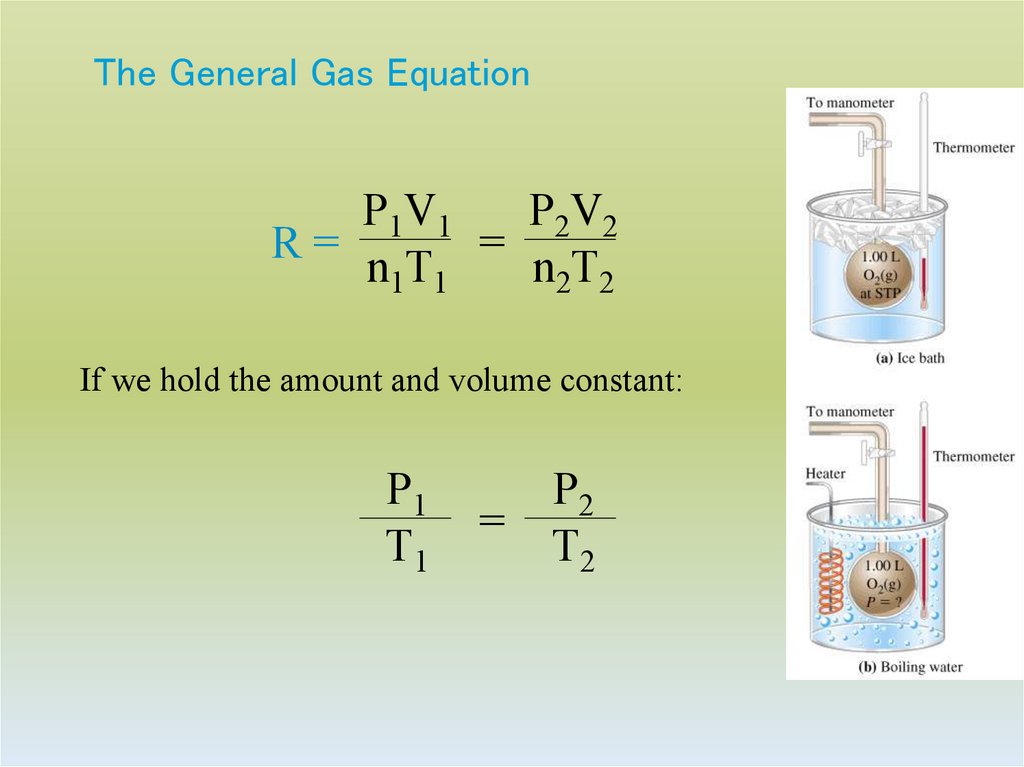
25. The General Gas Equation

P1V1
P2V2
R=
=
n1T1
n2T2
If we hold the amount and volume constant:
P1
T1
=
P2
T2

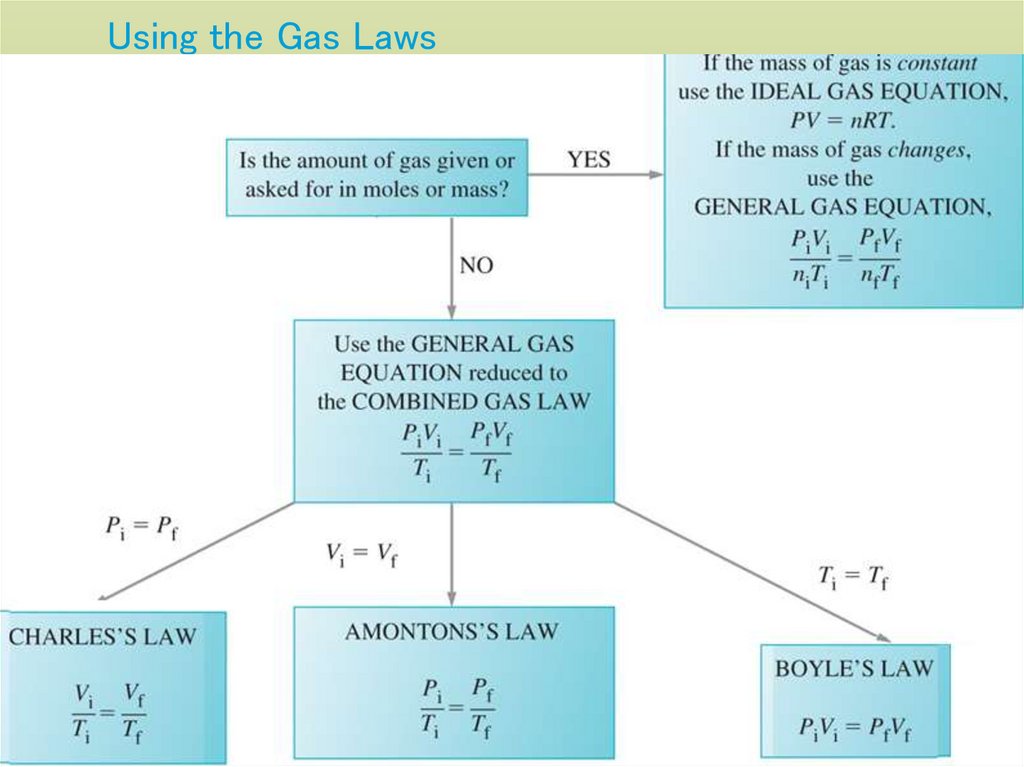
26. Using the Gas Laws

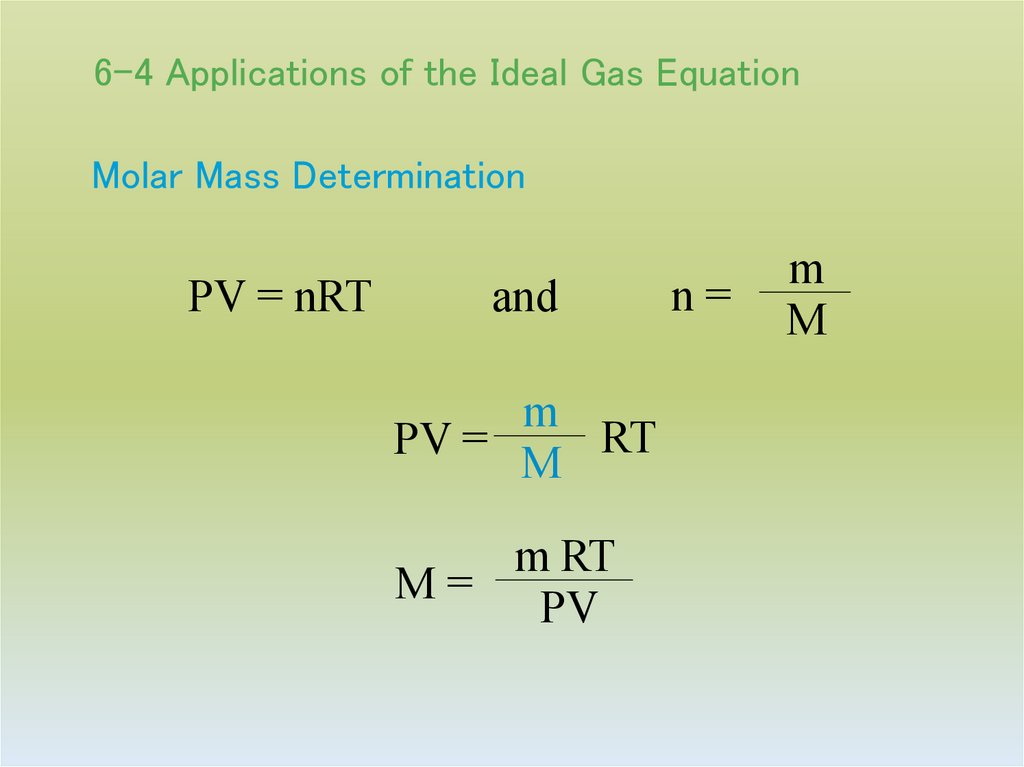
27. 6-4 Applications of the Ideal Gas Equation

Molar Mass Determination
PV = nRT
and
m
RT
PV =
M
m RT
M=
PV
n=
m
M

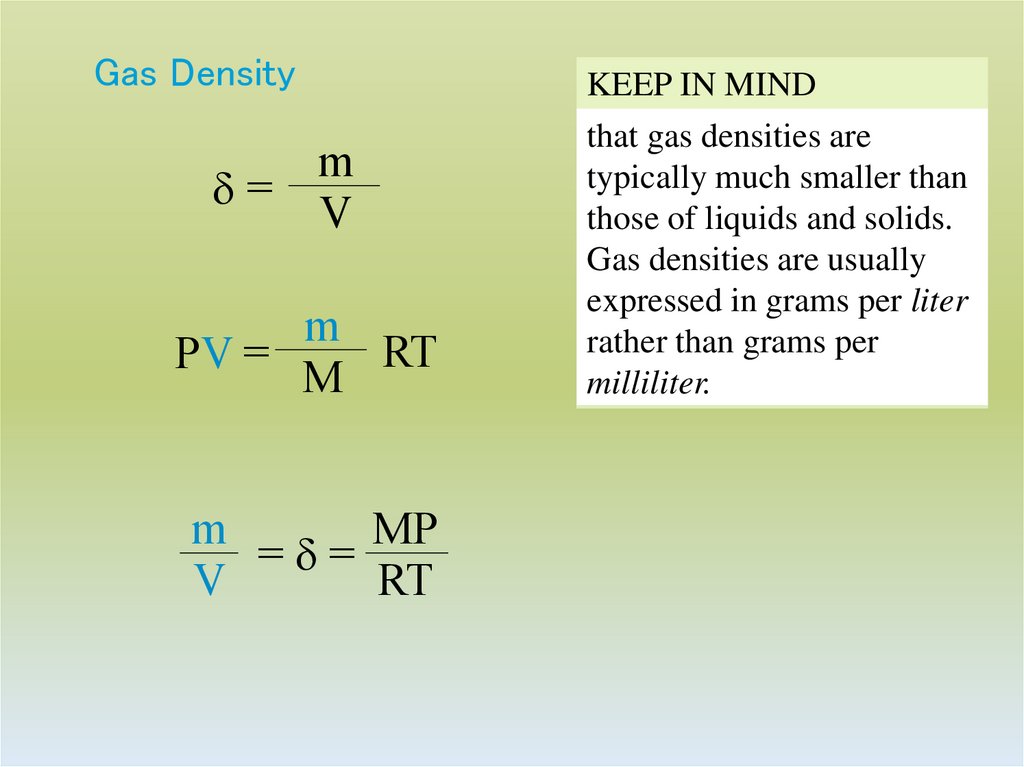
28. Gas Density

m
d=
V
m
RT
PV =
M
m
MP
=d=
V
RT
KEEP IN MIND
that gas densities are
typically much smaller than
those of liquids and solids.
Gas densities are usually
expressed in grams per liter
rather than grams per
milliliter.

29. 6-5 Gases in Chemical Reactions

Stoichiometric factors relate gas quantities to quantities of
other reactants or products.
Ideal gas equation relates the amount of a gas to volume,
temperature and pressure.

30.

Examples:
1. The decomposition of sodium azide. NaN3 at high
temperatures produces N2(g). Together with necessary
devices to initiate the reaction and trap the sodium
metal formed, this reaction is used in air-bag safety
system. What volume of N2(g) measured at 735 mmHg
and 26 0C. Is produced when 70 g NaN3 is
decomposed?
2. How many grams of NaN3, are needed to produce 20 L
of N2(g) at 30 0C and 776 mmHg?

31.

Law of Combining Volumes can be developed using
the gas law.
Gay Lussac’s Law of combining volumes states that
gases react by volumes in the ratio of small whole
numbers.

32.

Examples
1.Zinc blende ZnS is the most important zinc ore. Roasting of
ZnS is the first step in the commercial production of zinc.
2 ZnS(s) + 3O2(g) → 2ZnO(s) + 2SO2(g)
What volume of SO2(g) forms per liter of O2(g) consumed? Both
gases are measured at 25 0C and 745 mmHg.
2. The first step in making nitric acid is to convert ammonia to
nitrogen monoxide. This is done under conditions of high
temperature and in the present of a platinum catalyst. What
volume O2(g) is consumed per liter of NO(g) formed?
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g)

33. 6-6 Mixtures of Gases

Partial pressure
Each component of a gas mixture exerts a
pressure that it would exert if it were in the
container alone.
• Gas laws apply to mixtures of gases.
• Simplest approach is to use ntotal, but....

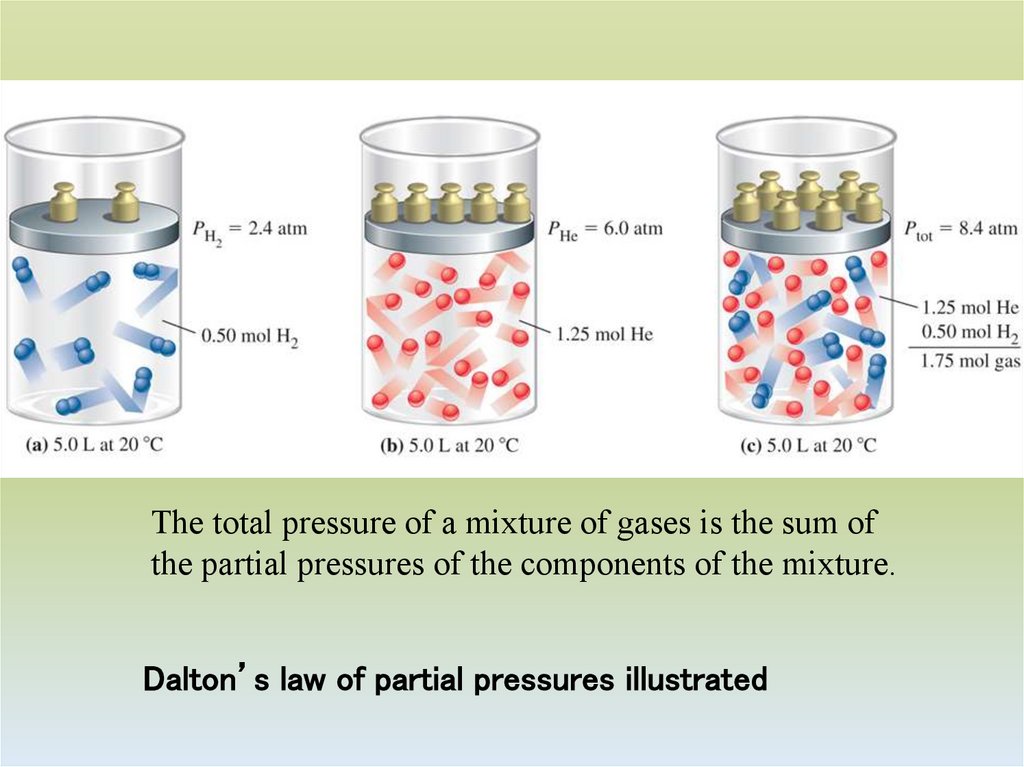
34. Dalton’s law of partial pressures illustrated

The total pressure of a mixture of gases is the sum of
the partial pressures of the components of the mixture.
Dalton’s law of partial pressures illustrated

35. Partial Pressure

Partial pressure is the pressure of a component
of gas that contributes to the overall pressure.
Partial volume is the volume that a gas would
occupy at the total pressure in the chamber.
Ratio of partial pressure to total pressure is the
MOLE FRACTION.
Ptot = Pa + Pb +…
Pa
Ptot
na
naRT/Vtot
=
=
ntotRT/Vtot
ntot
Recall
na
= a
ntot

36.

Examples
1.What is the pressure exerted by a mixture of 1g H2 and
5 g He when the mixture is confined to a volume of 5 L
at 20 0C?
2.If we add 12.5 g Ne to the mixture of gases described
in Example 1 and then raise the temperature to 550C what
will be the total gas pressure?
3. What are the partial pressures of H2 and He gaseous
mixture described in example 1.
4. A mixture of 0.197 mol CO2 g and 0.00278 mol H2O g
is held at 30 0C and 2.5 atm. What is the partial pressure
of each gas?