ИП матемаика декабрь

1.

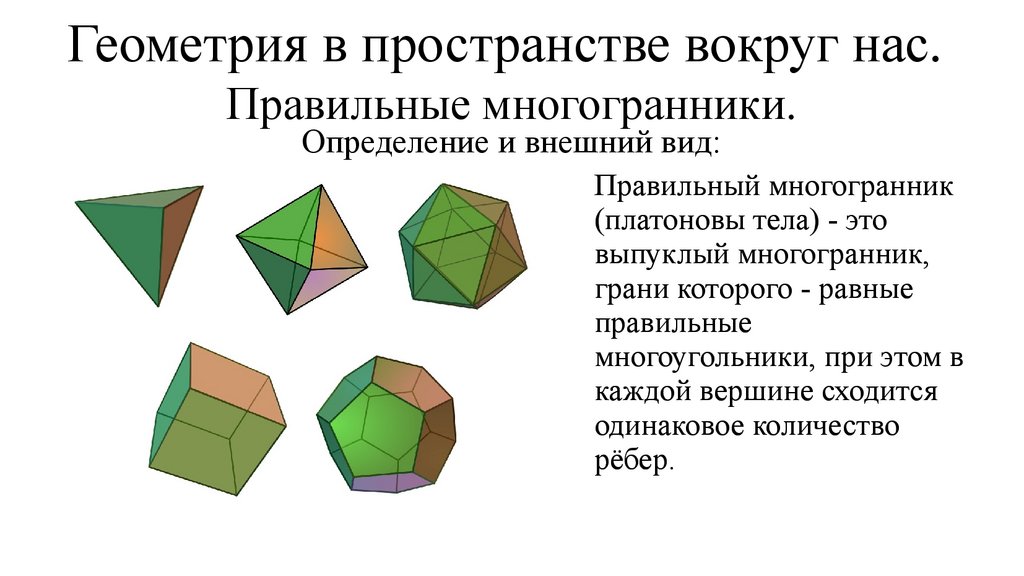
Геометрия в пространстве вокруг нас.
Правильные многогранники.
Определение и внешний вид:
Правильный многогранник
(платоновы тела) - это
выпуклый многогранник,
грани которого - равные
правильные
многоугольники, при этом в
каждой вершине сходится
одинаковое количество
рёбер.

2.

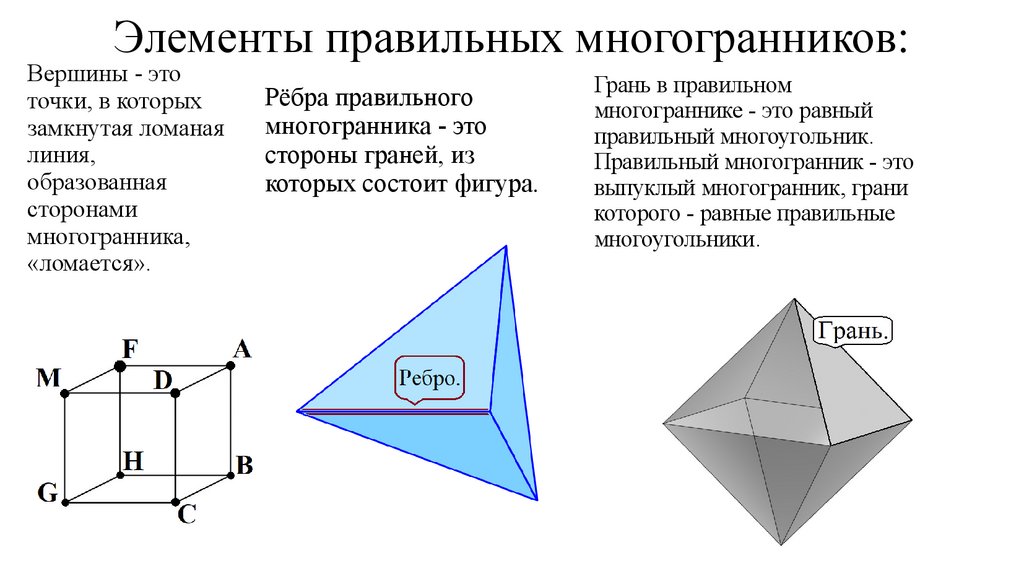
Элементы правильных многогранников:
Вершины - это
точки, в которых
замкнутая ломаная
линия,
образованная
сторонами
многогранника,
«ломается».
Рёбра правильного
многогранника - это
стороны граней, из
которых состоит фигура.
Грань в правильном
многограннике - это равный
правильный многоугольник.
Правильный многогранник - это
выпуклый многогранник, грани
которого - равные правильные
многоугольники.

3.

Из чего состоит поверхность правильных
многогранников:
Правильный многогранник это {p, q}, где:
P - число рёбер в каждой грани.
q - число рёбер, сходящихся в каждой вершине.
Поверхность правильного многогранника состоит из
правильных многоугольников.
Площадь поверхности S правильного многогранника {p, q}
вычисляется, как площадь правильного p-угольника,
умноженная на число граней Г:

4.

С каждым правильным многогранником связаны три
концентрические сферы:
Описанная сфера, проходящая через вершины многогранника;
Срединная сфера, касающаяся каждого его ребра в середине;
Вписанная сфера, касающаяся каждой его грани в её центре.
где θ - двугранный угол между
смежными гранями
многогранника.

5.

Объём правильного многогранника
вычисляется, как умноженный на
число граней объём правильной
пирамиды, основанием которой
служит правильный p-угольник, а
высотой - радиус вписанной сферы
r:

6.

Формулы правильных многогранников:
Константы φ и ξ задаются выражениями:

7.

Интересные факты о правильных многогранниках!!!
1) Согласно концепции, придуманной платоном в 360 году до н.э. каждый
правильный многогранник соответствовал 4 стихиям.
☺ Огню соответствовал тетраэдр.
☺ Земле - гексаэдр.
☺ Воздуху - октаэдр.
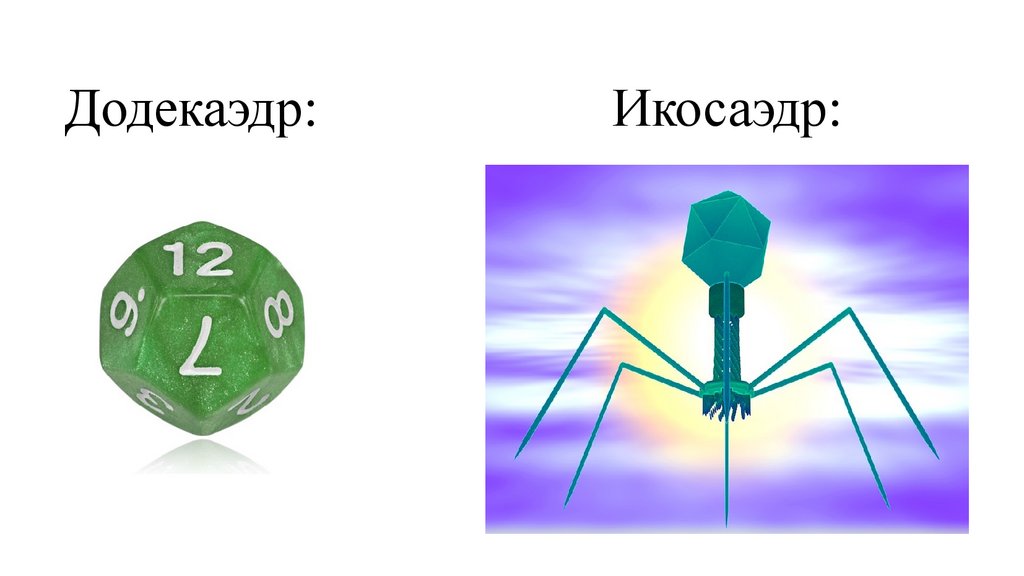
☺ Воде - икосаэдр.
☻ Додекаэдр - символизировал вселенную.
2) Существуют геометрические связи между правильными
многогранниками. Например, куб и октаэдр дуальны: получаются друг из
друга, если центры тяжести граней одного принять за вершины другого и
обратно.

8.

3) Правильные многогранники известны с древнейших времён. Их орнаментные
модели можно найти на резных каменных шарах, созданных в период позднего
неолита, в Шотландии.
4) Для выпуклых многогранников существует важная формула Эйлера: V-E+F=2,
V - количество вершин, E - количество рёбер, F - количество граней. Эта формула
верна для всех многогранников, включая правильные.
5) Все правильные многогранники обладают высокой степенью симметрии.
Например куб имеет 24 симметрии, что означает что его можно повернуть или
отразить 24 различными способами и он останется неизменным. ☺

9.

Примеры правильных многогранников из окружающего мира и жизни:
Куб:
Тетраэдр:
Октаэдр:

10.

Додекаэдр:
Икосаэдр: