Geometricheskie-tela-Ot-osnov-k-slozhnym-formam (1)

1.

Геометрические тела: От основ к
сложным формам
Добро пожаловать в увлекательный мир геометрии, где простые формы сливаются
в сложные структуры, лежащие в основе всего, что нас окружает. Эта презентация
погрузит вас в фундаментальные концепции геометрических тел, от их базовых
определений до мощных теорем, таких как теорема Эйлера и пространственная
теорема Пифагора, раскрывая их значение в науке, инженерии и повседневной
жизни. Приготовьтесь увидеть красоту и логику, скрытую в формах и измерениях.

2.

Что такое геометрическое тело? Определение и примеры
Определение:
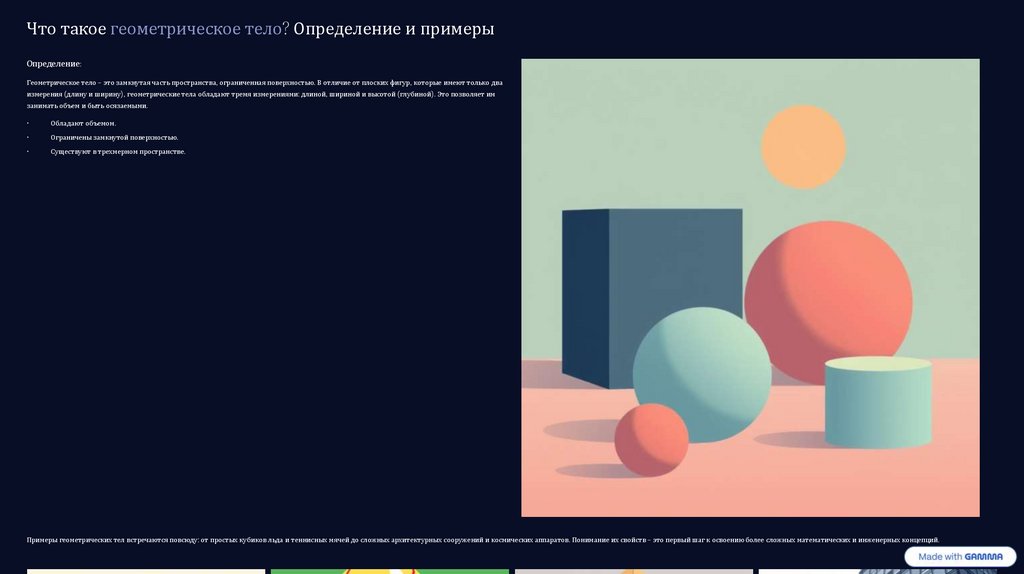
Геометрическое тело – это замкнутая часть пространства, ограниченная поверхностью. В отличие от плоских фигур, которые имеют только два
измерения (длину и ширину), геометрические тела обладают тремя измерениями: длиной, шириной и высотой (глубиной). Это позволяет им
занимать объем и быть осязаемыми.
Обладают объемом.
Ограничены замкнутой поверхностью.
Существуют в трехмерном пространстве.
Примеры геометрических тел встречаются повсюду: от простых кубиков льда и теннисных мячей до сложных архитектурных сооружений и космических аппаратов. Понимание их свойств – это первый шаг к освоению более сложных математических и инженерных концепций.

3.

Основные характеристики геометрических тел: Вершины, ребра,
грани
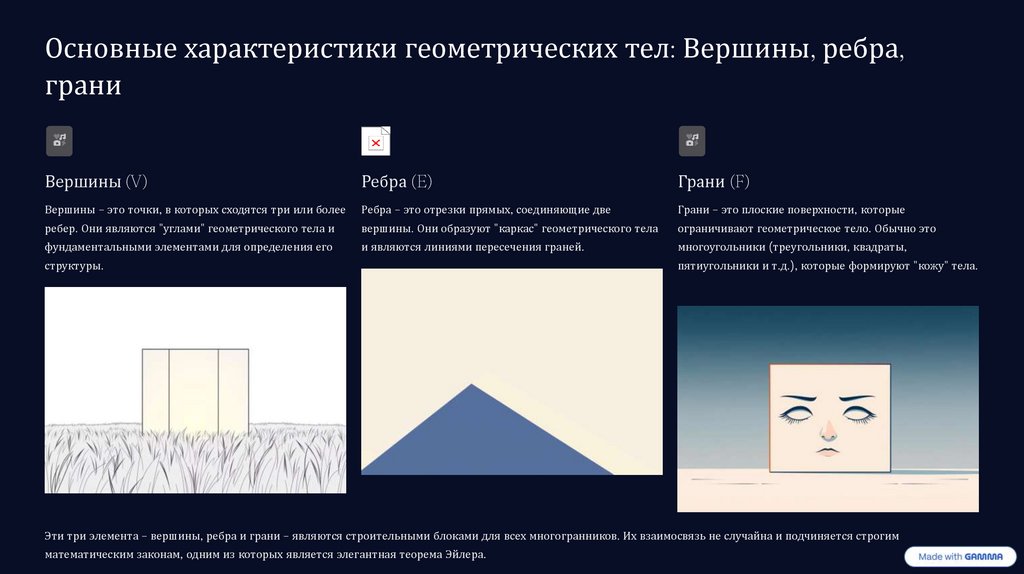
Вершины (V)
Ребра (E)
Грани (F)
Вершины – это точки, в которых сходятся три или более
Ребра – это отрезки прямых, соединяющие две
Грани – это плоские поверхности, которые
ребер. Они являются "углами" геометрического тела и
вершины. Они образуют "каркас" геометрического тела
ограничивают геометрическое тело. Обычно это
фундаментальными элементами для определения его
и являются линиями пересечения граней.
многоугольники (треугольники, квадраты,
структуры.
пятиугольники и т.д.), которые формируют "кожу" тела.
Эти три элемента – вершины, ребра и грани – являются строительными блоками для всех многогранников. Их взаимосвязь не случайна и подчиняется строгим
математическим законам, одним из которых является элегантная теорема Эйлера.

4.

Теорема Эйлера для многогранников: V - E + F = 2
Открытие Леонарда Эйлера
В середине 18 века великий швейцарский математик Леонард Эйлер обнаружил удивительную и простую
взаимосвязь между количеством вершин (V), ребер (E) и граней (F) любого выпуклого многогранника. Его
формула, V - E + F = 2, стала одной из самых известных и фундаментальных теорем в топологии и геометрии.
Эта теорема гласит, что для любого выпуклого многогранника, сколько бы граней, вершин или ребер он ни
имел, сумма вершин и граней всегда будет на два больше, чем количество ребер. Это универсальное свойство,
которое проявляется во всех многогранниках, от простейших кубов до сложнейших икосаэдров.
Формула Эйлера подчеркивает глубокую структурную инвариантность многогранников, которая не зависит от
их размера, формы или конкретных углов, а только от их топологической структуры.
Леонард Эйлер (1707–1783)
"Геометрия — это знание всегда верного."
Эта теорема является краеугольным камнем в изучении топологии, области математики, которая исследует свойства фигур, сохраняющиеся при деформациях без разрывов или склеиваний.

5.

Применение теоремы Эйлера: Проверка и анализ структур
01
02
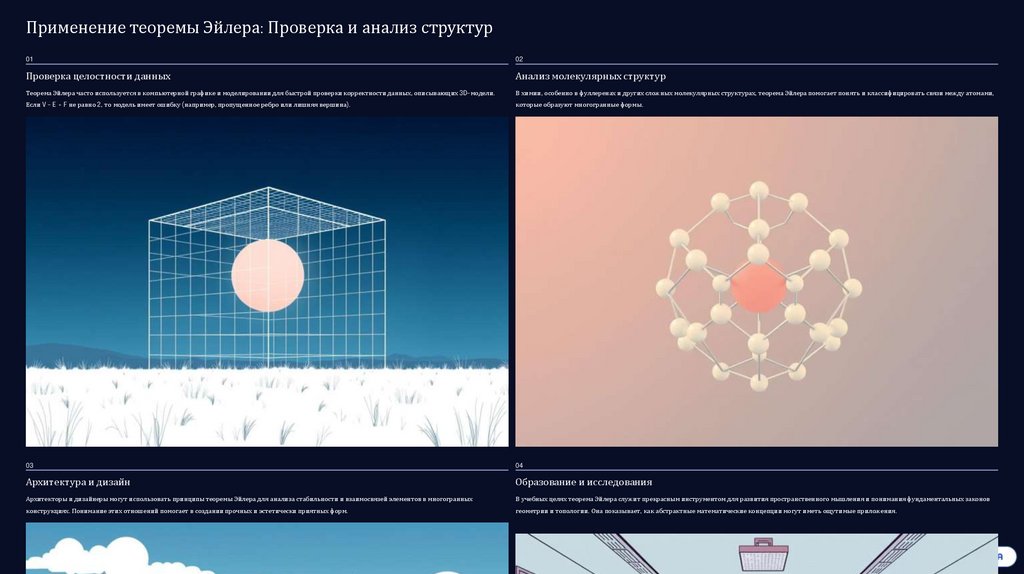
Проверка целостности данных
Анализ молекулярных структур
Теорема Эйлера часто используется в компьютерной графике и моделировании для быстрой проверки корректности данных, описывающих 3D-модели.
В химии, особенно в фуллеренах и других сложных молекулярных структурах, теорема Эйлера помогает понять и классифицировать связи между атомами,
Если V - E + F не равно 2, то модель имеет ошибку (например, пропущенное ребро или лишняя вершина).
которые образуют многогранные формы.
03
04
Архитектура и дизайн
Образование и исследования
Архитекторы и дизайнеры могут использовать принципы теоремы Эйлера для анализа стабильности и взаимосвязей элементов в многогранных
В учебных целях теорема Эйлера служит прекрасным инструментом для развития пространственного мышления и понимания фундаментальных законов
конструкциях. Понимание этих отношений помогает в создании прочных и эстетически приятных форм.
геометрии и топологии. Она показывает, как абстрактные математические концепции могут иметь ощутимые приложения.

6.

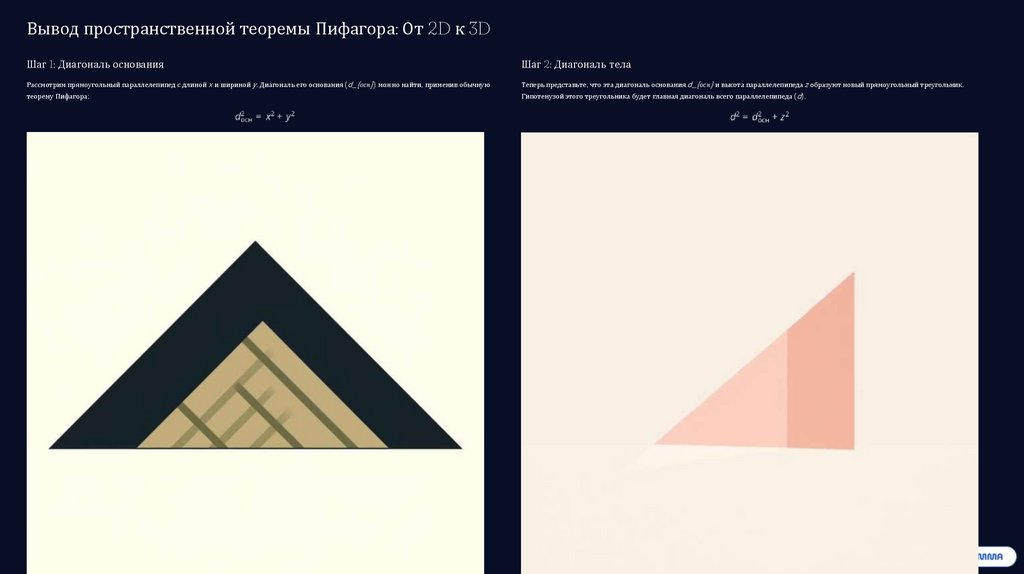
Вывод пространственной теоремы Пифагора: От 2D к 3D
Шаг 1: Диагональ основания
Шаг 2: Диагональ тела
Рассмотрим прямоугольный параллелепипед с длиной x и шириной y. Диагональ его основания (d_{осн}) можно найти, применив обычную
Теперь представьте, что эта диагональ основания d_{осн} и высота параллелепипеда z образуют новый прямоугольный треугольник.
теорему Пифагора:
Гипотенузой этого треугольника будет главная диагональ всего параллелепипеда (d).

7.

Практическое применение пространственной теоремы Пифагора:
Расчеты в строительстве и инженерии
Строительство и архитектура
Навигация и картография
При проектировании зданий и мостов, теорема используется для расчета длин
В системах GPS и других навигационных технологиях пространственная теорема
стальных балок, труб и кабелей, проложенных по диагонали через трехмерные
Пифагора необходима для точного определения расстояния между двумя
пространства, обеспечивая точность и безопасность конструкции.
точками на Земле (с учетом ее кривизны) или в воздухе, а также для расчета
траекторий движения.
Робототехника и мехатроника
Компьютерная графика и VR
Для программирования движений роботов и манипуляторов, эта теорема
При создании 3D-моделей, игр и виртуальной реальности, теорема используется
помогает рассчитать точное положение конечного эффектора в пространстве,
для расчета расстояний между объектами, определения видимости и для
исходя из углов и длин звеньев, что критически важно для выполнения задач с
реалистичного рендеринга трехмерных сцен, что обеспечивает погружение
высокой точностью.
пользователя.
От разработки новых технологий до решения повседневных задач, пространственная теорема Пифагора остается незаменимым инструментом, позволяющим нам
эффективно взаимодействовать с трехмерным миром.

8.

Взаимосвязь между теоремой Эйлера и пространственной теоремой Пифагора
Хотя теорема Эйлера и пространственная теорема Пифагора относятся к разным разделам геометрии
(топологии и евклидовой геометрии соответственно), они обе предоставляют фундаментальные
инструменты для понимания и анализа трехмерного пространства.
Теорема Эйлера (V - E + F = 2):
Описывает топологические свойства многогранников.
Касается взаимосвязи между количеством вершин, ребер и граней.
Не зависит от размера или формы многогранника, только от его "структуры связей".
Пространственная теорема Пифагора (d^2 = x^2 + y^2 + z^2):
Описывает метрические свойства пространства.
Касается количественных измерений: длин, расстояний.
Критически зависит от конкретных размеров объекта в трех измерениях.

9.

Итоги и дальнейшие исследования: Красота геометрии вокруг нас
Теорема Эйлера
Основы геометрии
Мы рассмотрели, что такое геометрические тела, их основные
Эта фундаментальная теорема (V - E + F = 2) раскрывает элегантную
топологическую взаимосвязь между элементами любого выпуклого
многогранника.
элементы: вершины, ребра и грани, которые формируют основу для
понимания трехмерного пространства.
Пространственная теорема Пифагора
Расширяя знакомую нам 2D-теорему, она позволяет точно
измерять расстояния и диагонали в трехмерном пространстве
(d^2 = x^2 + y^2 + z^2).
Дальнейшие исследования
Геометрия – это постоянно развивающаяся область. Откройте для себя
фракталы, неевклидову геометрию, топологию и другие
захватывающие концепции, чтобы углубить свое понимание мира.
Практическое применение
Обе теоремы имеют колоссальное значение в различных областях – от
инженерии и архитектуры до компьютерной графики и науки о
материалах.
Геометрия не просто наука, это язык, который описывает структуру Вселенной. От микромира до макрокосмоса, от атомов до галактик – все пронизано геометрическими формами и закономерностями. Надеемся, эта
презентация вдохновила вас на дальнейшее исследование этой удивительной и красивой дисциплины.