неравенства урок 1

1. Решение квадратных неравенств

2. 1. Среди приведенных уравнений укажите уравнения, задающие квадратичную функцию:

1. Среди приведенных уравнений укажите
уравнения, задающие квадратичную
функцию:
• 1) у = 2х2 + х - 1;
• 2) у2 = х + 1;
• 3) у2 = х2 - 1;
• 4) у = -х - х2;
• 5) у2 = х2;
• 6) у = -х2.
• Для указанных функций назовите
коэффициенты квадратного трехчлена (в
формуле у = ах2 + bх + с).

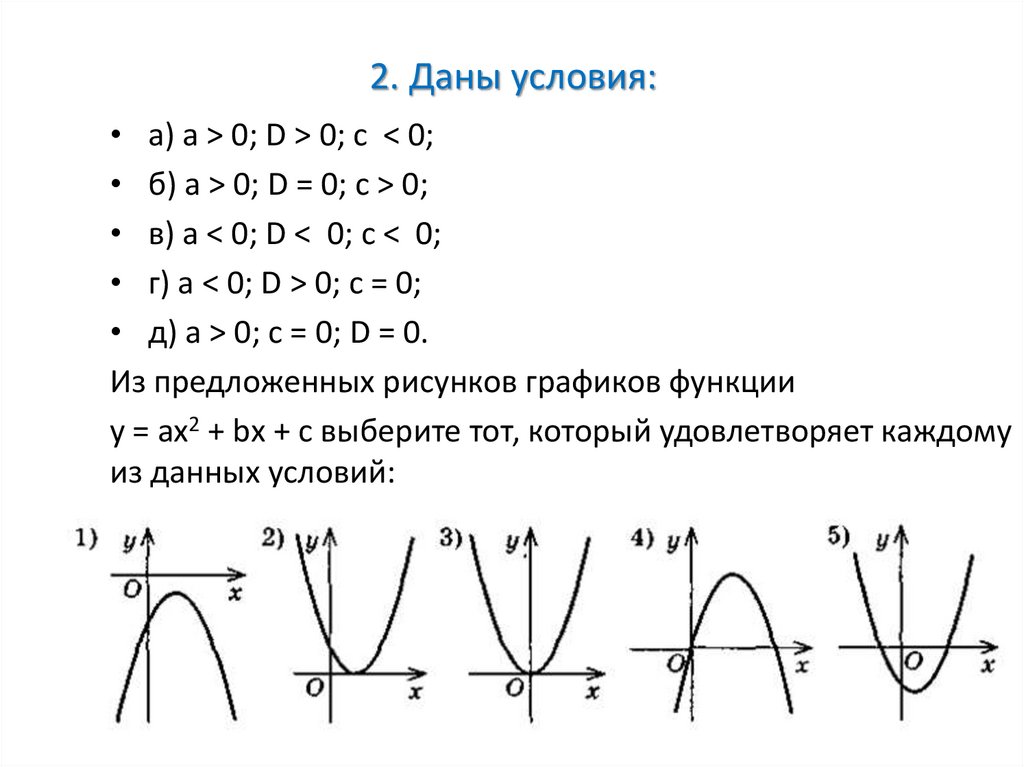
3. 2. Даны условия:

2. Даны условия:
• а) а > 0; D > 0; c < 0;
• б) а > 0; D = 0; c > 0;
• в) а < 0; D < 0; c < 0;
• г) а < 0; D > 0; c = 0;
• д) а > 0; с = 0; D = 0.
Из предложенных рисунков графиков функции
у = ах2 + bх + с выберите тот, который удовлетворяет каждому
из данных условий:

4. 3. Найдите нули функции (если они существуют):

3. Найдите нули функции (если они существуют):

5. Определение.

Неравенства вида ах2 + bх + с > 0 (< 0; ≥ 0; ≤ 0)
называются квадратными, если а≠ 0.
Пример.
3х2 - 2х - 1 > 0,
x2 - 9 ≥ 0,
х2 - 2х 0,
х2 > 0

6. Схема решения квадратных неравенств

• 1. Найти дискриминант D, корни x1, x2 квадратного
трехчлена (если они существуют).
• 2. Построить эскиз графика квадратичной функции
у = ах2 + bх + с (с учетом знака коэффициента а и
найденного знака дискриминанта D и корней).
• 3. Для случая > 0 соответственно получим
промежуток, для которого точки параболы лежат
выше оси Ох,
• для случая < 0 соответственно получим промежутки,
для которых точки параболы лежат ниже оси Ох.

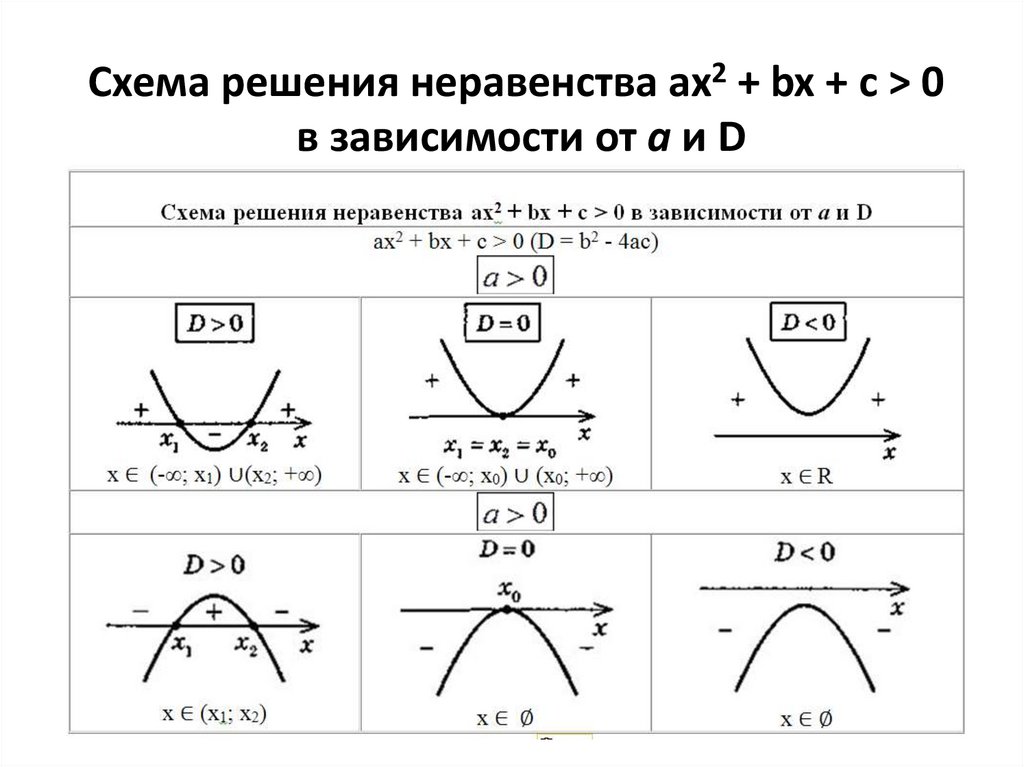
7. Схема решения неравенства ах2 + bx + c > 0  в зависимости от а и D

Схема решения неравенства ах2 + bx + c > 0
в зависимости от а и D

8. Решение квадратных неравенств

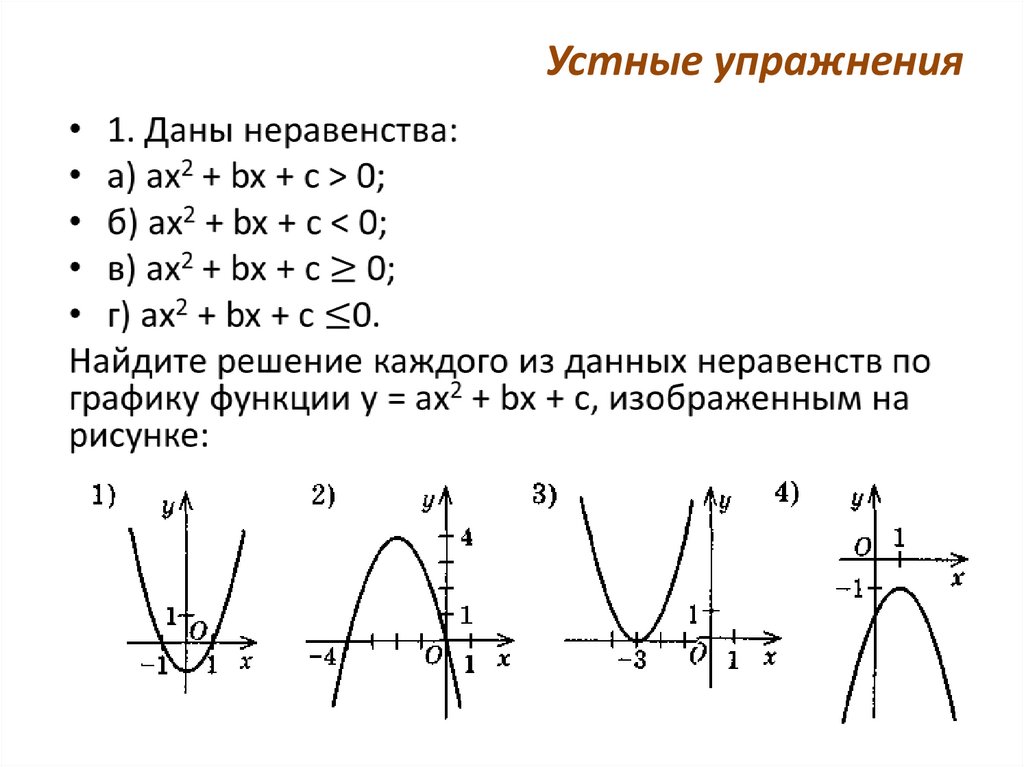
9. Устные упражнения

10. Устные упражнения

11. Самостоятельная работа

12. Контрольные вопросы

• 1. Определите знак
• коэффициента а,
• коэффициента с,
• дискриминанта D
по графику функции у = ах2 + bх + с, изображенному на
рисунке:

13. Контрольные вопросы