Урок_10_Свойства_параллельных_плоскостей

1.

Геометрия 10 класс
Тема:
«Свойства параллельных
плоскостей»

2.

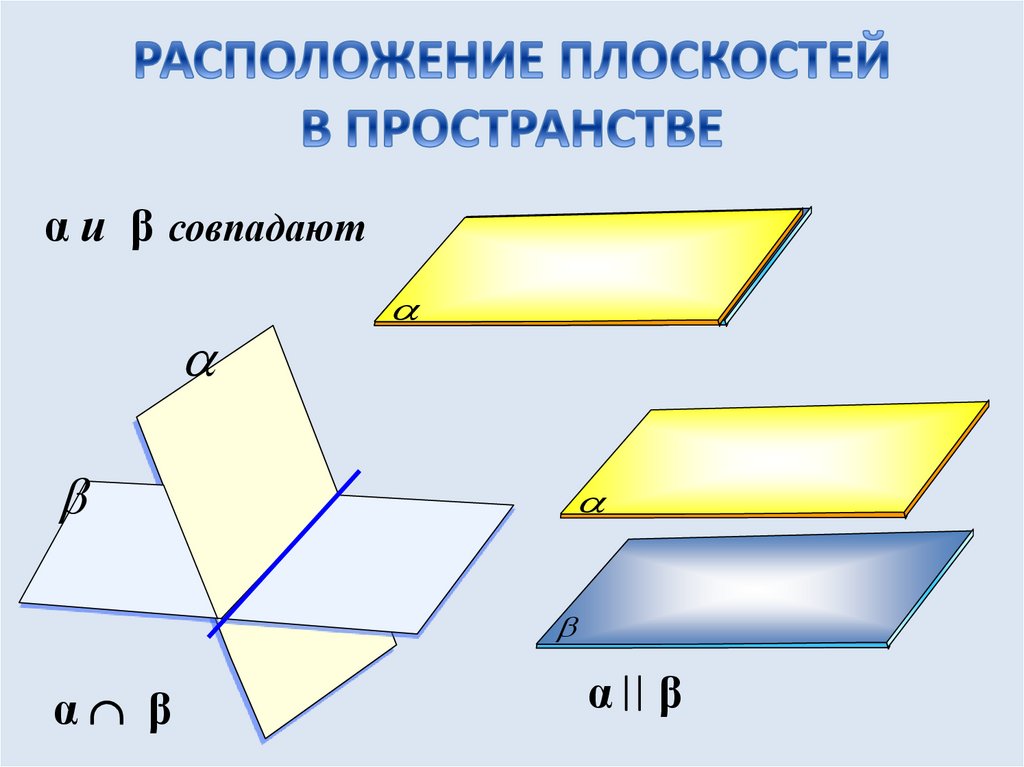
α и β совпадают
α β
α β

3.

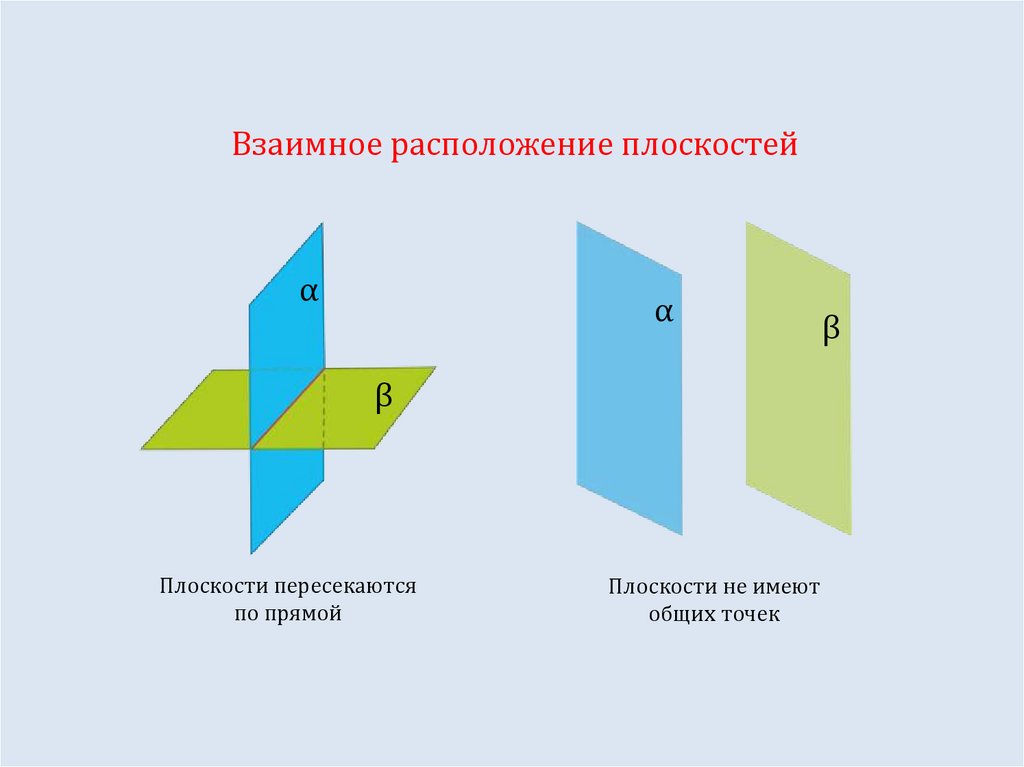
Взаимное расположение плоскостей
α
α
β
Плоскости пересекаются
по прямой
Плоскости не имеют
общих точек
β

4.

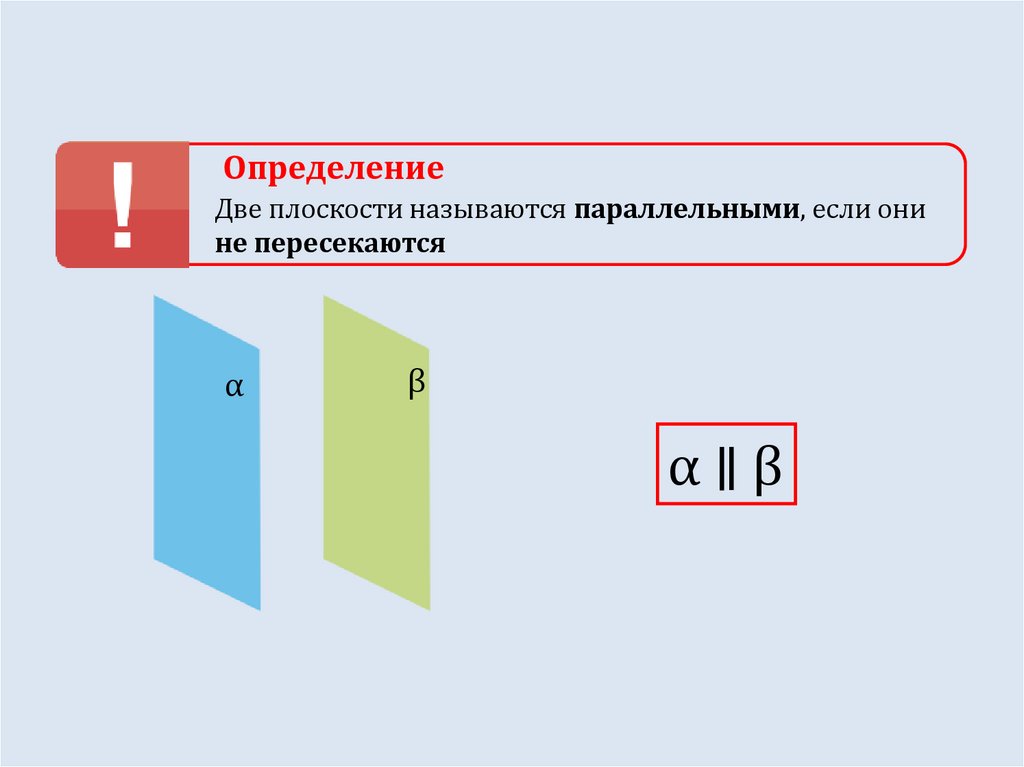
Определение
Две плоскости называются параллельными, если они
не пересекаются
α
β
α∥β

5.

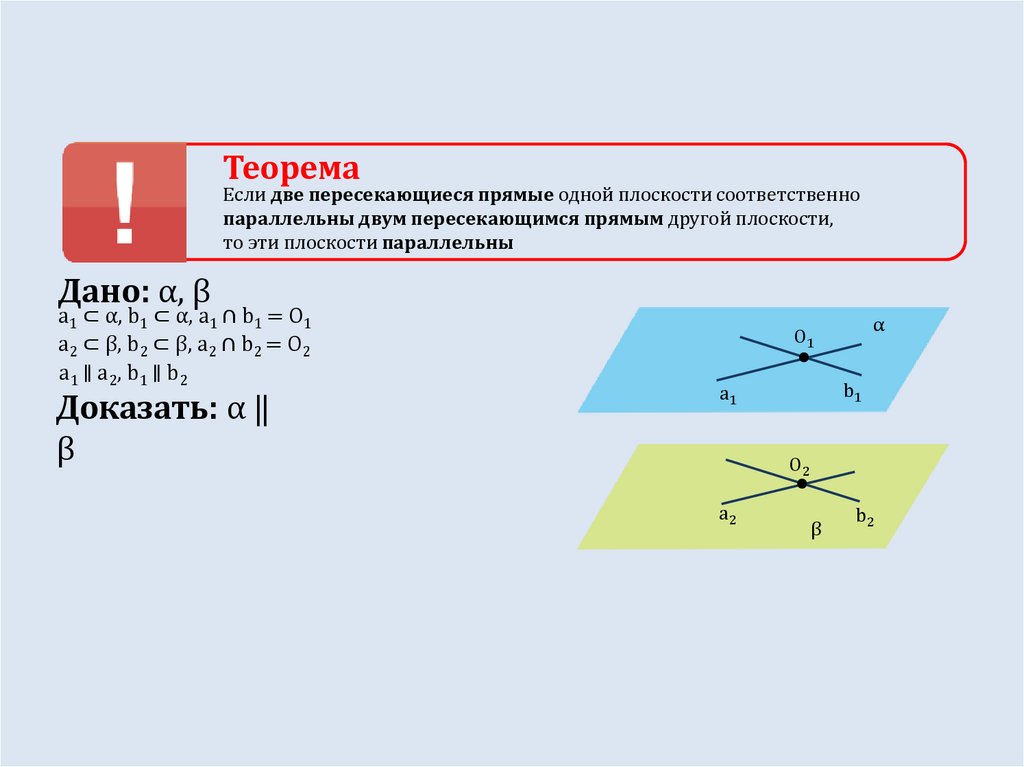
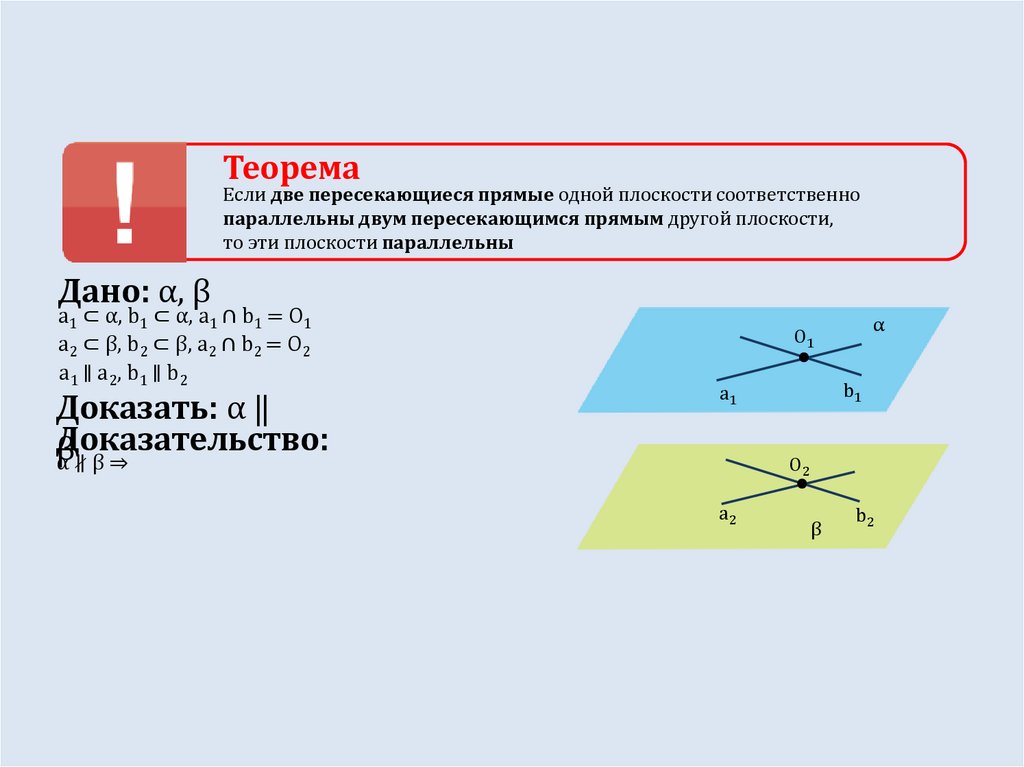
Теорема
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
Доказать: α ‖
β
α
O1
b1
a1
O2
a2
β
b2

6.

Теорема
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
Доказать: α ‖
Доказательство:
β
α∦β⇒
α
O1
b1
a1
O2
a2
β
b2

7.

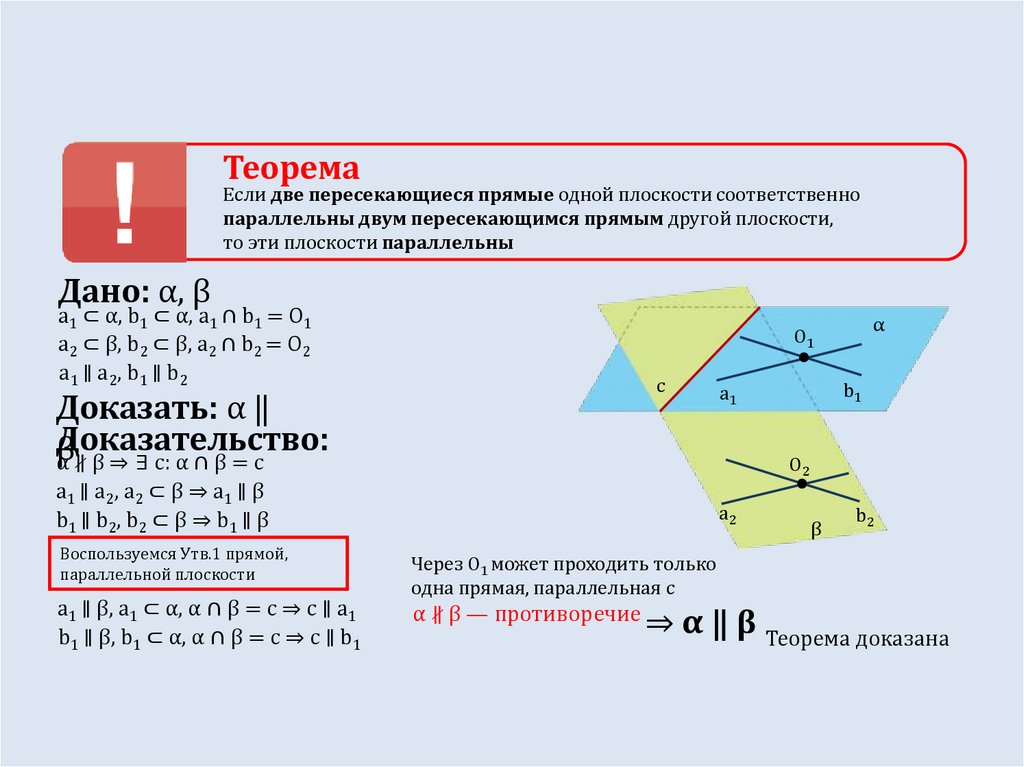
Теорема
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
c
Доказать: α ‖
Доказательство:
β
α ∦ β ⇒ ∃ c: α ∩ β = c
a1 ∥ β, a1 ⊂ α, α ∩ β = c ⇒ c ∥ a1
b1 ∥ β, b1 ⊂ α, α ∩ β = c ⇒ c ∥ b1
b1
a1
O2
a1 ∥ a2, a2 ⊂ β ⇒ a1 ∥ β
b1 ∥ b2, b2 ⊂ β ⇒ b1 ∥ β
Воспользуемся Утв.1 прямой,
параллельной плоскости
α
O1
a2
β
b2
Через O1 может проходить только
одна прямая, параллельная с
α ∦ β — противоречие
⇒ α ‖ β Теорема доказана

8.

1. Верно ли, что если две пересекающиеся прямые,
лежащие в одной плоскости, параллельны другой плоскости,
то эти плоскости параллельны. Верно
2. Верно ли, что если две прямые, лежащие в одной
плоскости, параллельны двум прямым другой плоскости,
то эти плоскости параллельны. Нет
Привести контрпример – пересекающиеся плоскости,
проведенные через параллельные прямые.

9.

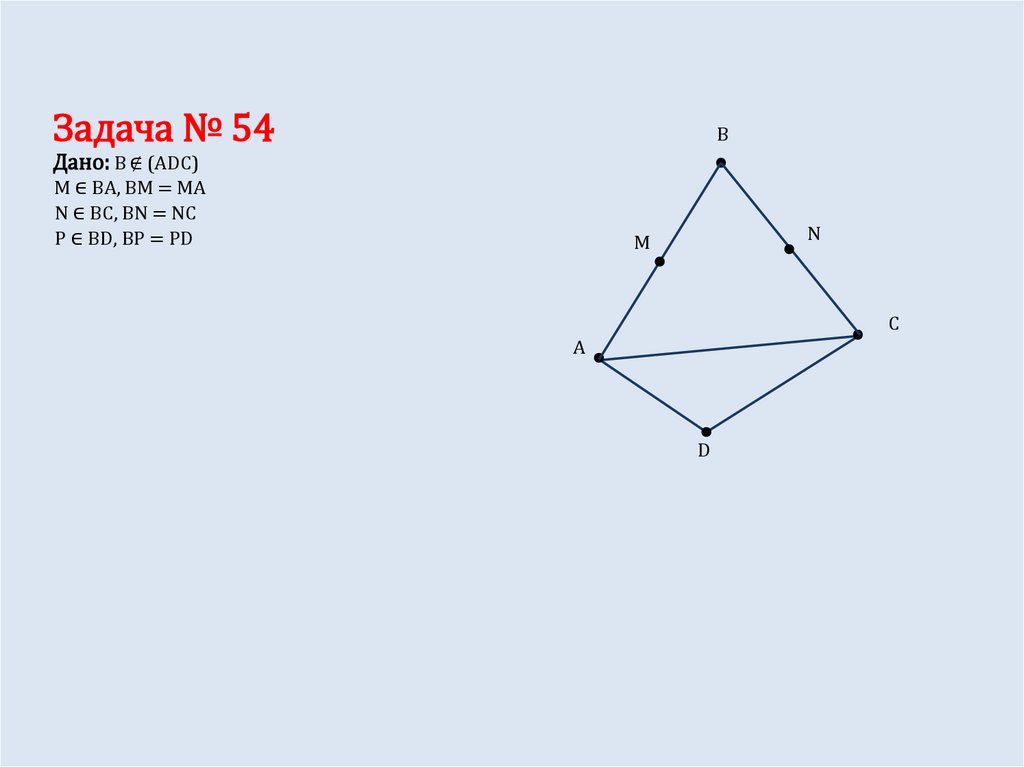
Задача № 54
B
Дано: B ∉ (ADC)
M ∈ BA, BM = MA
N ∈ BC, BN = NC
P ∈ BD, BP = PD
N
M
C
A
D

10.

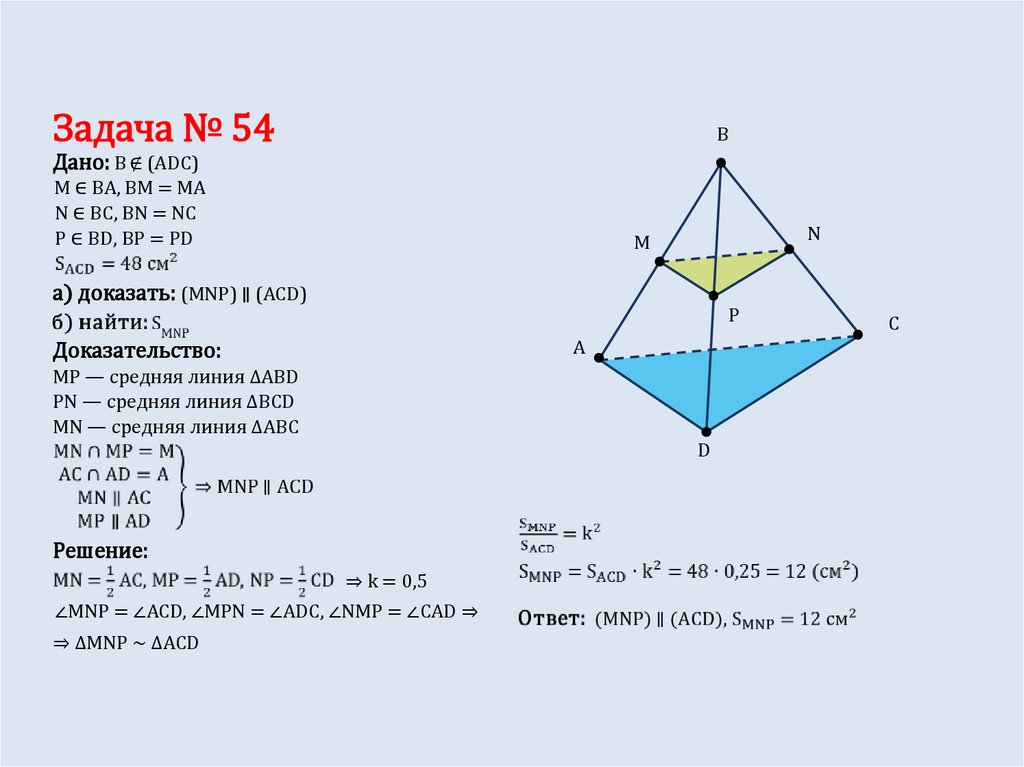
Задача № 54
B
Дано: B ∉ (ADC)
M ∈ BA, BM = MA
N ∈ BC, BN = NC
P ∈ BD, BP = PD
N
M
а) доказать: (MNP) ∥ (ACD)
P
A
Доказательство:
MP — средняя линия ∆ABD
PN — средняя линия ∆BCD
MN — средняя линия ∆ABC
D
Решение:
⇒ k = 0,5
∠MNP = ∠ACD, ∠MPN = ∠ADC, ∠NMP = ∠CAD ⇒
⇒ ∆MNP ∼ ∆ACD
C

11.

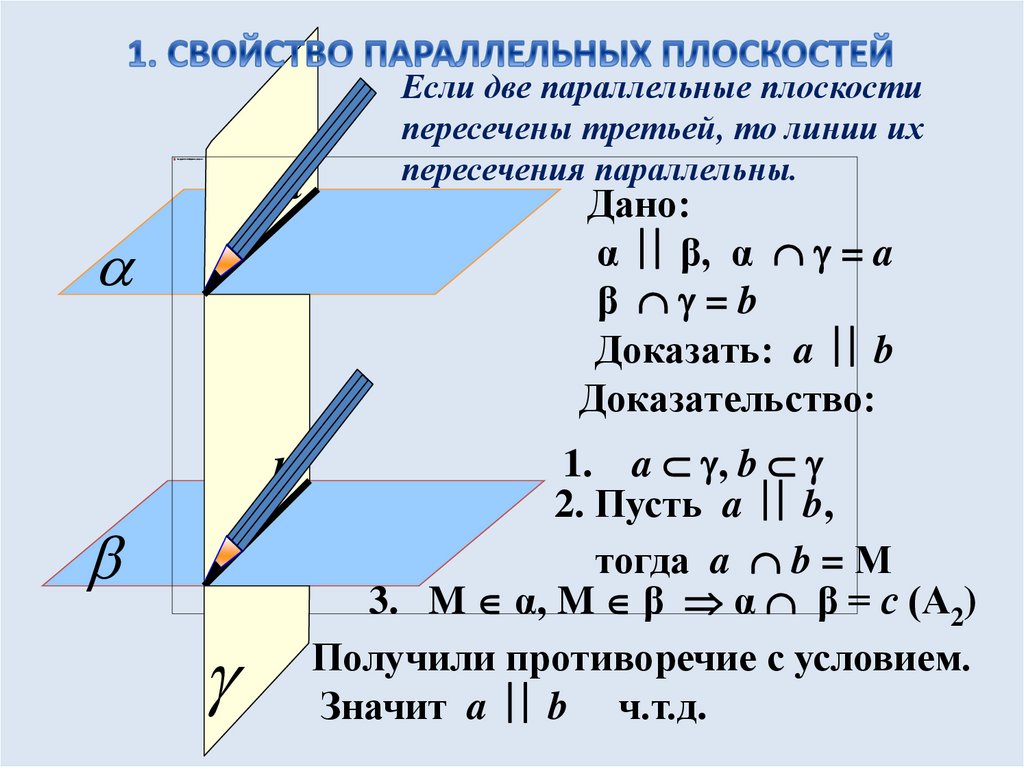
а
b
Если две параллельные плоскости
пересечены третьей, то линии их
пересечения параллельны.
Дано:
α β, α = a
β =b
Доказать: a b
Доказательство:
1. a , b
2. Пусть a b,
тогда a b = М
3. M α, M β α β = с (А2)
Получили противоречие с условием.
Значит a b ч.т.д.

12.

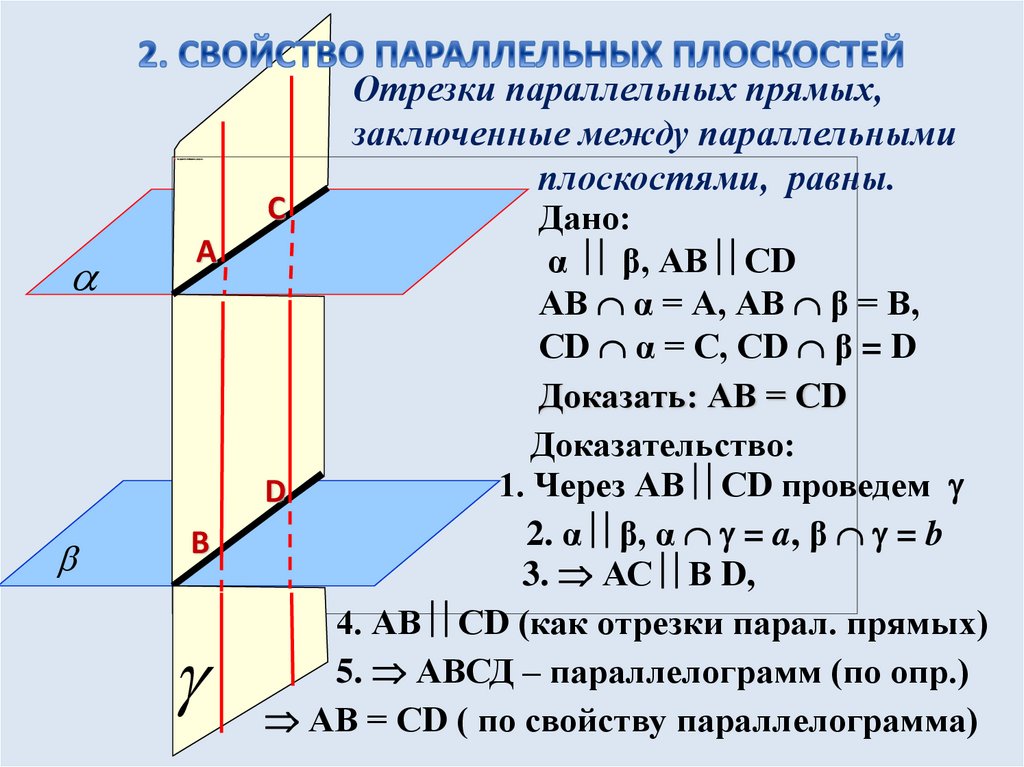
А
В
Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
С
Дано:
α β, АВ СD
АВ α = А, АВ β = В,
СD α = С, СD β = D
Доказать: АВ = СD
Доказательство:
1. Через АВ СD проведем
D
2. α β, α = a, β = b
3. АС В D,
4. АВ СD (как отрезки парал. прямых)
5. АВСД – параллелограмм (по опр.)
АВ = СD ( по свойству параллелограмма)

13.

1. Если плоскости не пересекаются, то они параллельны.
ДА
2. Плоскости параллельны, если прямая лежащая в
НЕТ
одной плоскости, параллельна другой плоскости?
3. Если две прямые, лежащие в одной плоскости,
НЕТ
параллельны двум прямым другой плоскости, то эти
плоскости параллельны?
4. Если прямая перпендикулярна одной из двух параллельных
ДА
плоскостей, то она перпендикулярна и другой плоскости.
5. Прямые, по которым две параллельные плоскости
ДА
пересечены третьей плоскостью, параллельны.
6. Если прямая пересекает одну из двух плоскостей, то
НЕТ
она пересекает и другую.
7. Две плоскости, параллельные третьей, параллельны.
ДА
8. Отрезки прямых, заключенные между
НЕТ
параллельными плоскостями, равны.

14. верно ли утверждение?

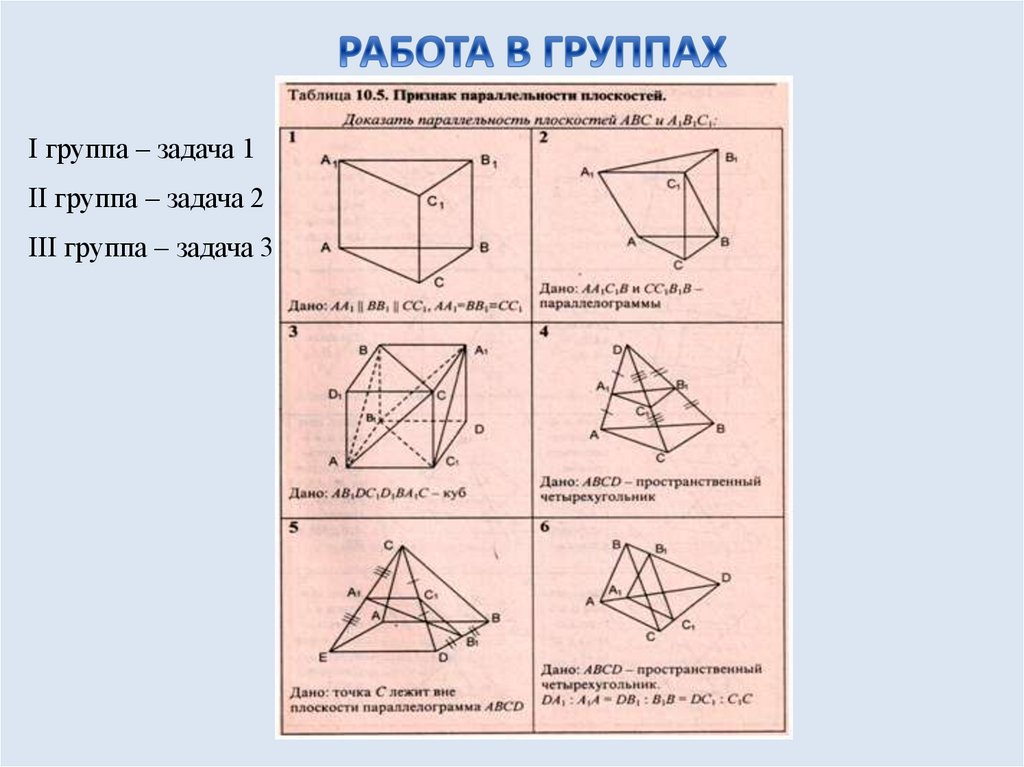
I группа – задача 1
II группа – задача 2
III группа – задача 3

15.

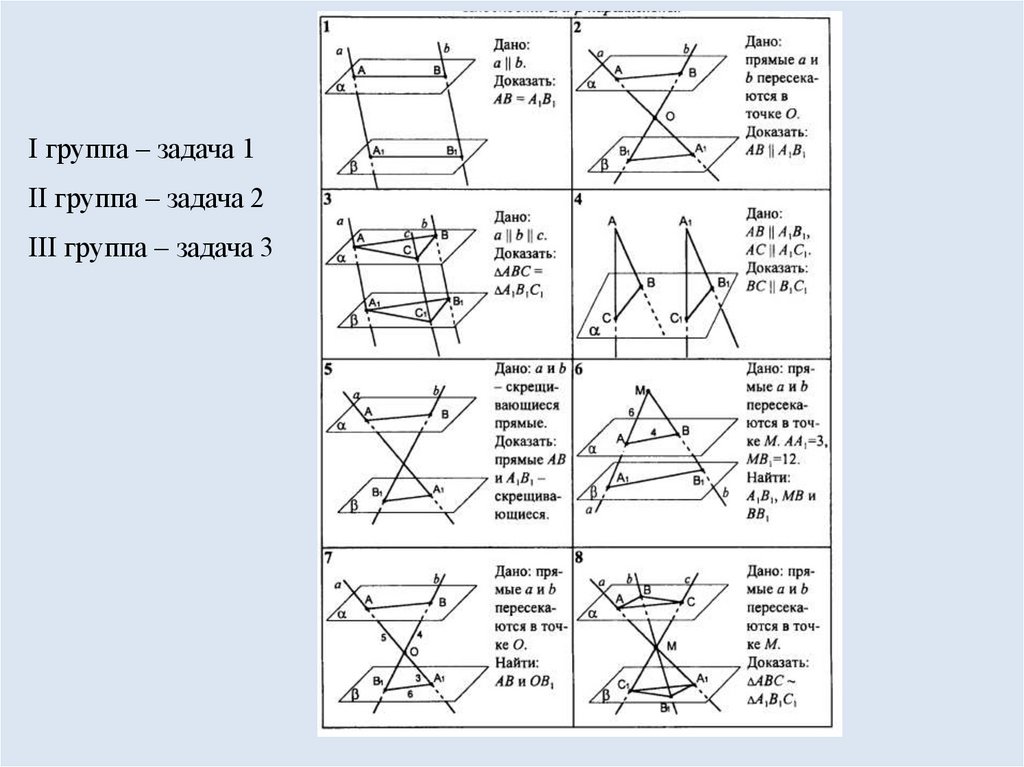
I группа – задача 1
II группа – задача 2
III группа – задача 3

16.

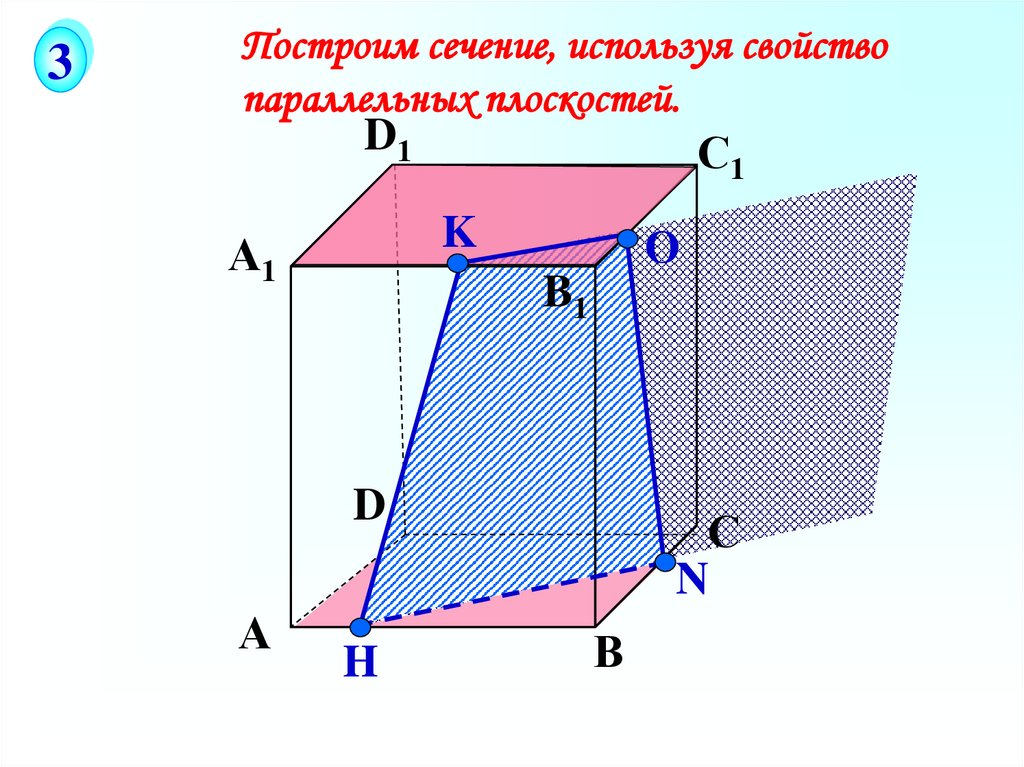
3
Построим сечение, используя свойство
параллельных плоскостей.
D1
С1
K
А1
О
B1
D
А
H
С
N
В

17.

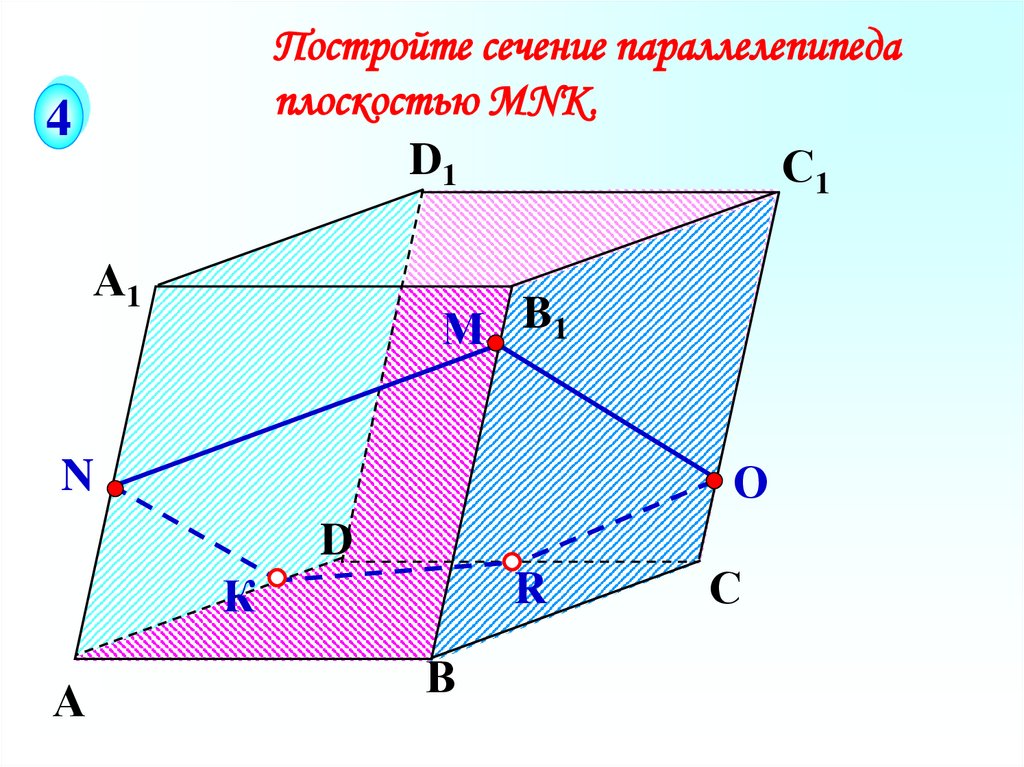
Постройте сечение параллелепипеда
плоскостью МNК.
D1
С1
4
А1
М B1
О
N
D
К
А
R
В
С

18.

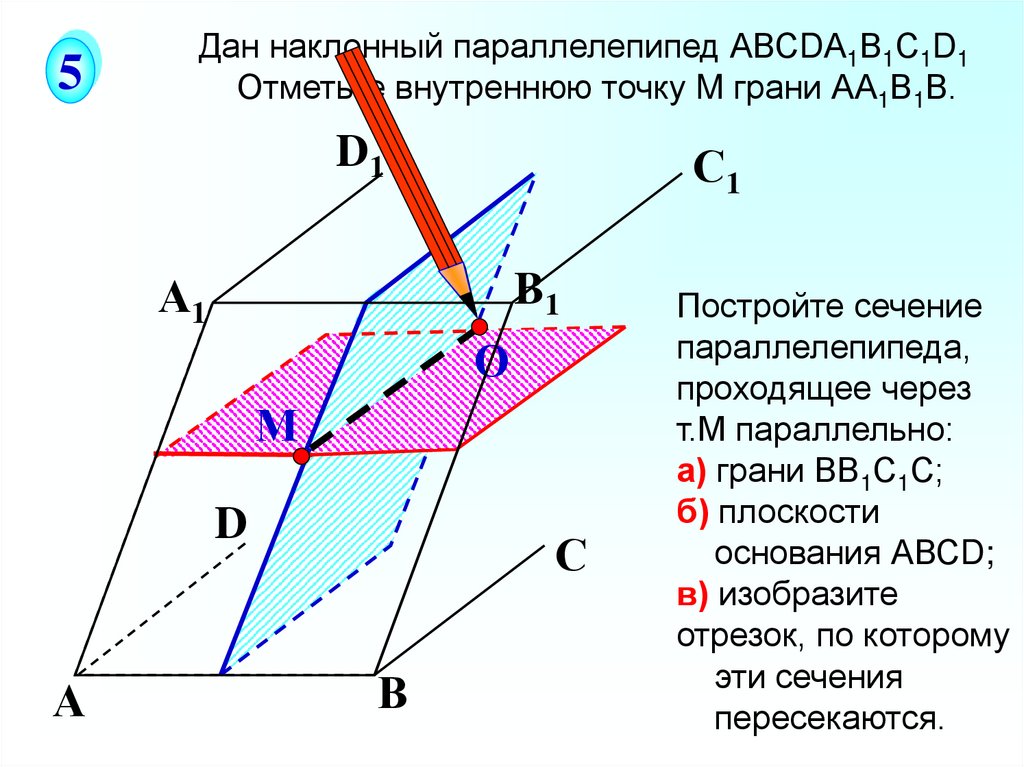
5
Дан наклонный параллелепипед АВСDА1В1С1D1
Отметьте внутреннюю точку M грани АА1В1В.
D1
С1
А1
B1
О
М
D
А
С
В
Постройте сечение
параллелепипеда,
проходящее через
т.М параллельно:
а) грани ВВ1С1С;
б) плоскости
основания АВСD;
в) изобразите
отрезок, по которому
эти сечения
пересекаются.

19.

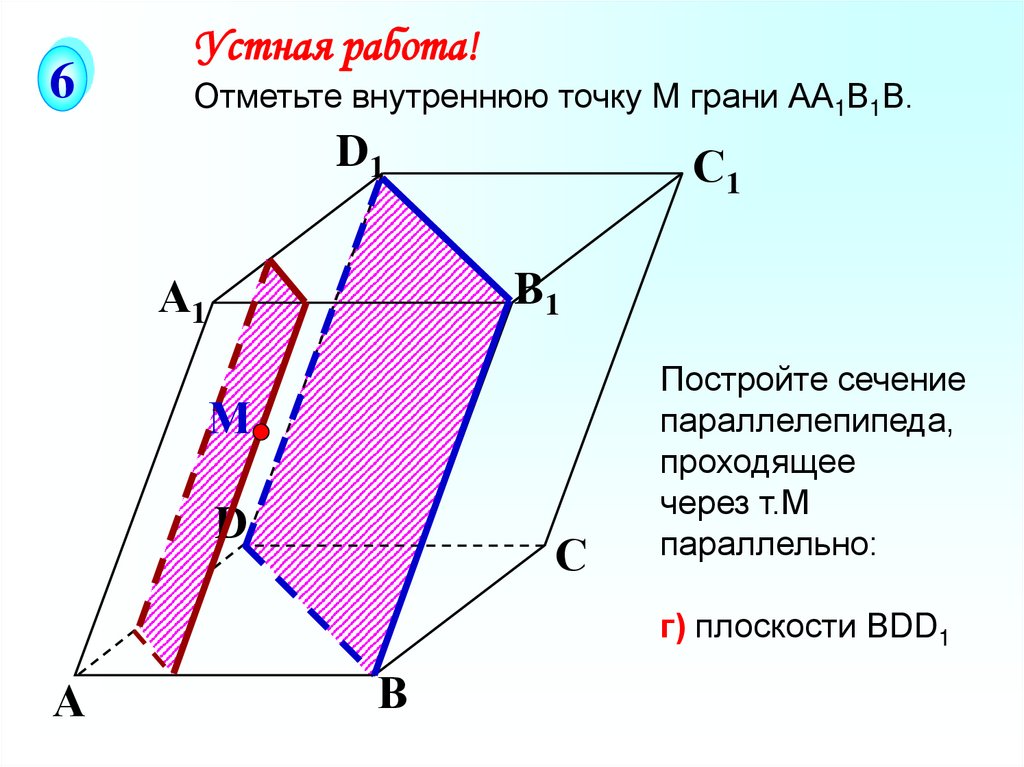
6
Устная работа!
Отметьте внутреннюю точку M грани АА1В1В.
D1
А1
С1
B1
М
D
С
Постройте сечение
параллелепипеда,
проходящее
через т.М
параллельно:
г) плоскости ВDD1
А
В

20.

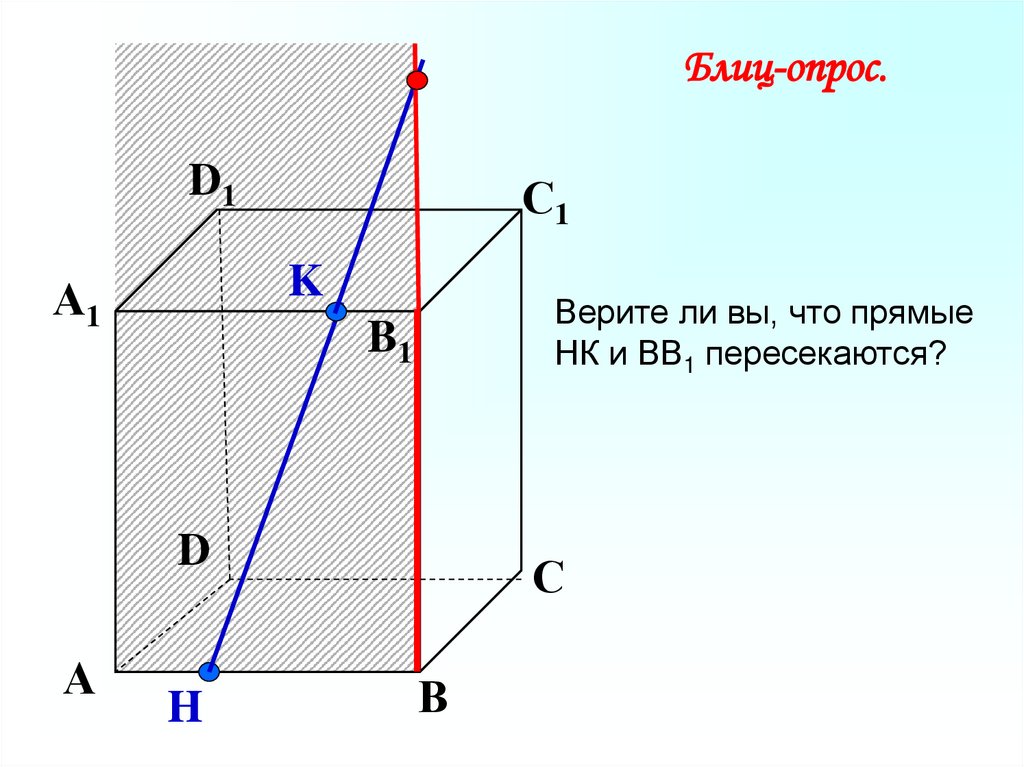
Блиц-опрос.
D1
С1
K
А1
Верите ли вы, что прямые
НК и ВВ1 пересекаются?
B1
D
А
H
С
В

21.

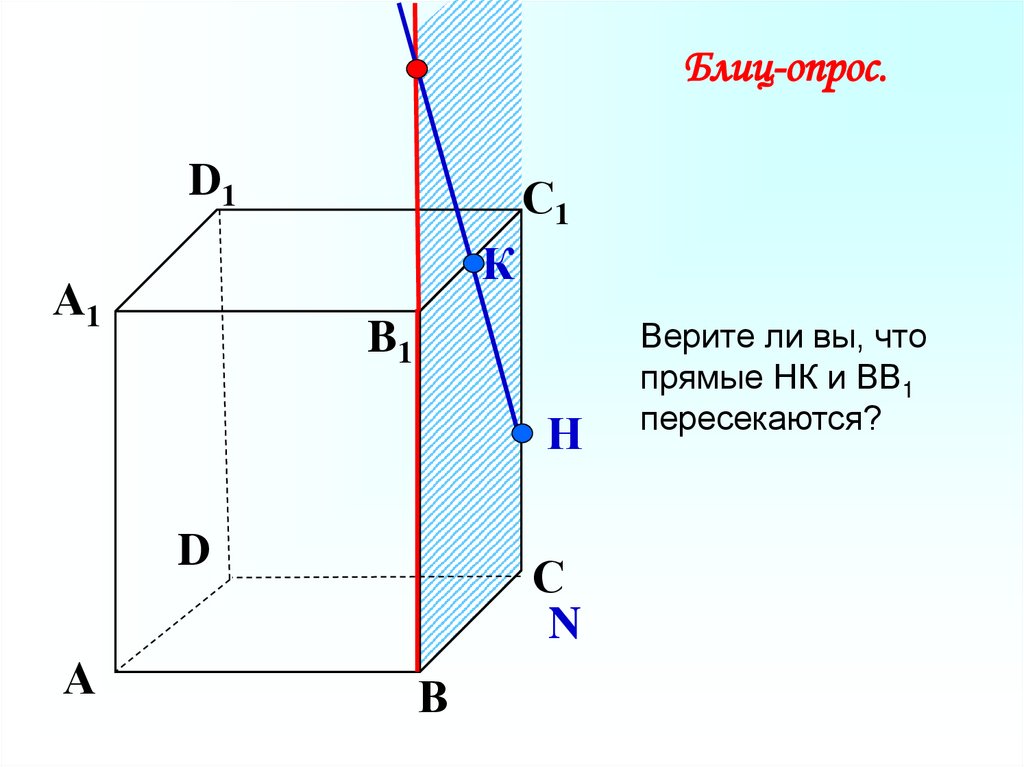
Блиц-опрос.
D1
С1
К
А1
B1
Н
D
А
С
N
В
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

22.

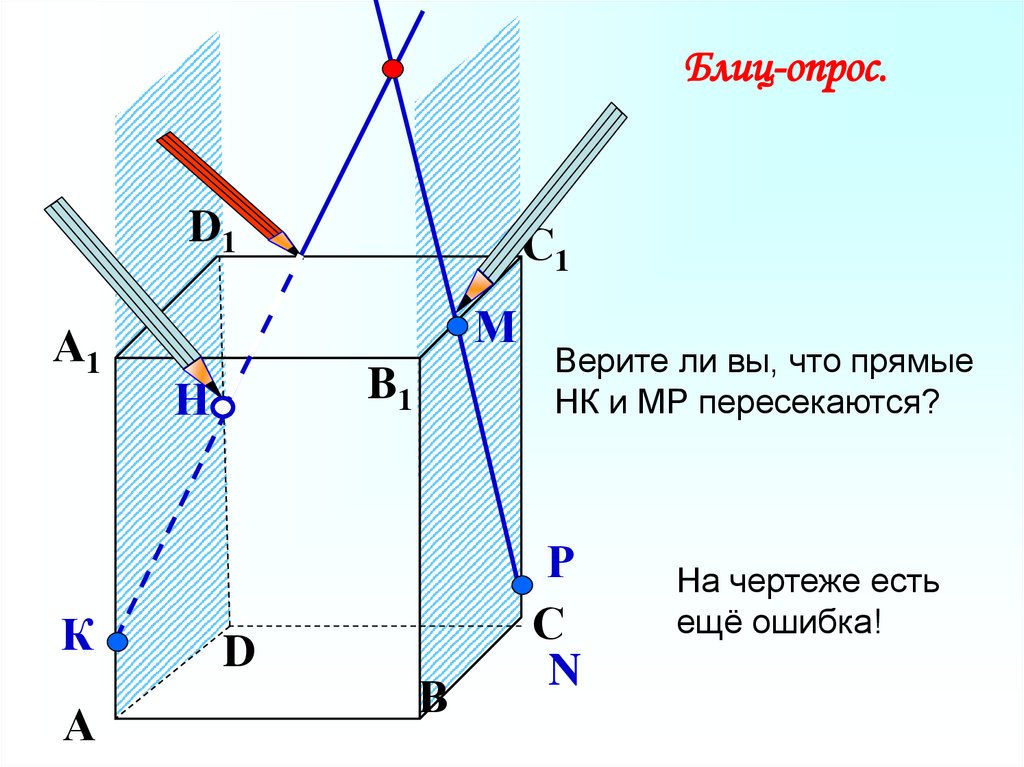
Блиц-опрос.
D1
А1
К
А
С1
М
B1
Н
D
В
Верите ли вы, что прямые
НК и МР пересекаются?
Р
С
N
На чертеже есть
ещё ошибка!

23.

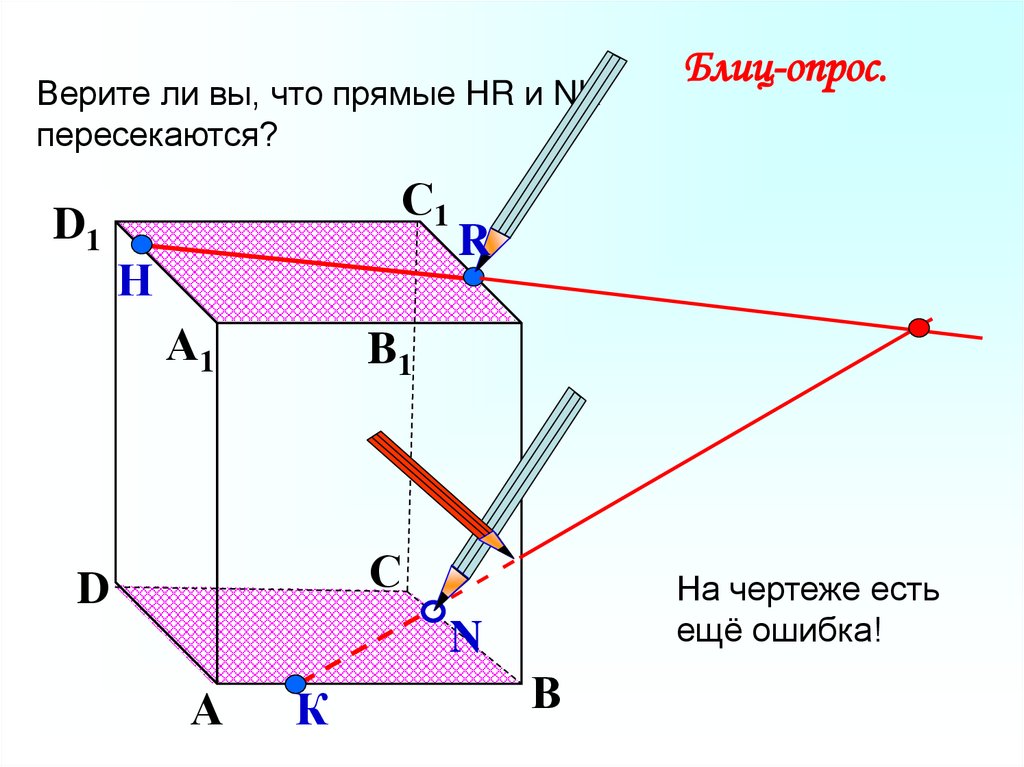
Верите ли вы, что прямые НR и NK
пересекаются?
D1
С1
Н
А1
R
B1
С
D
На чертеже есть
ещё ошибка!
N
А
Блиц-опрос.
К
В

24.

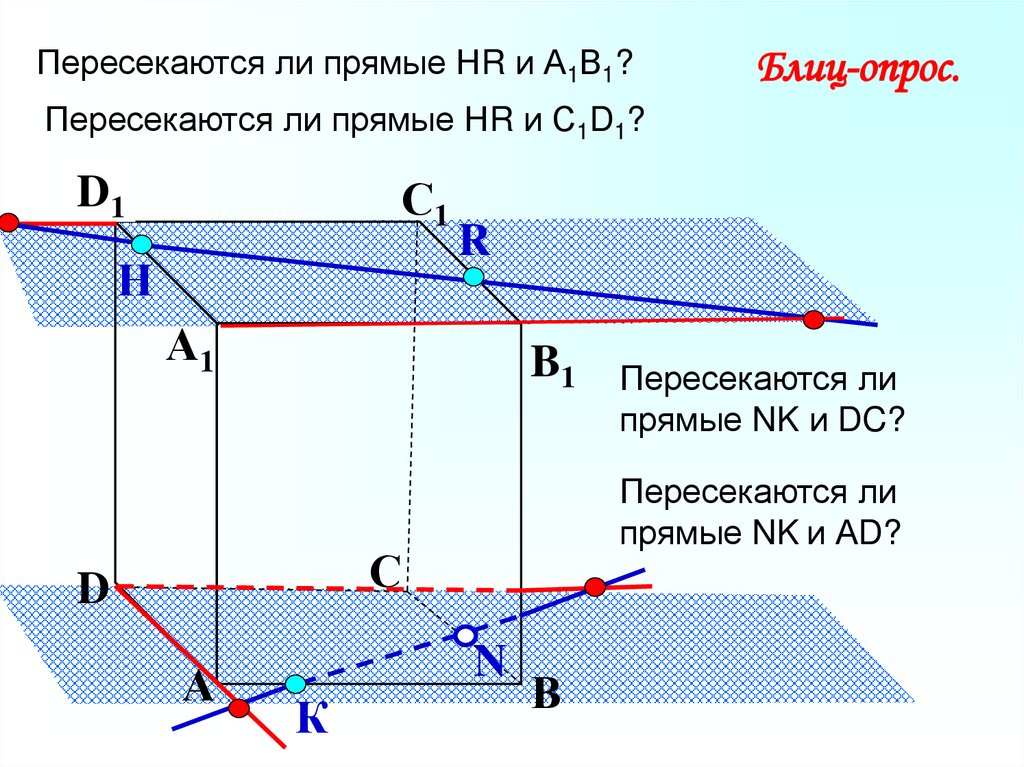
Пересекаются ли прямые НR и А1В1?
Блиц-опрос.
Пересекаются ли прямые НR и С1D1?
С1
D1
Н
R
А1
B1
Пересекаются ли
прямые NK и АD?
С
D
А
N
К
Пересекаются ли
прямые NK и DC?
В

25.

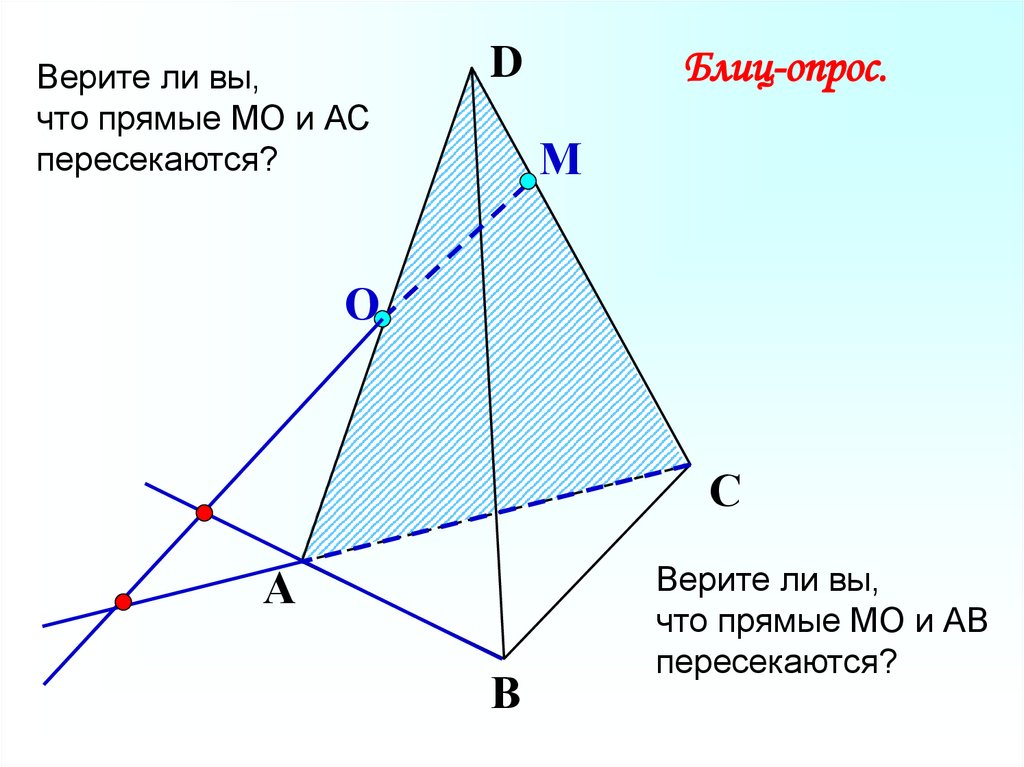
Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос.
D
М
О
С
А
В
Верите ли вы,
что прямые МО и АВ
пересекаются?

26.

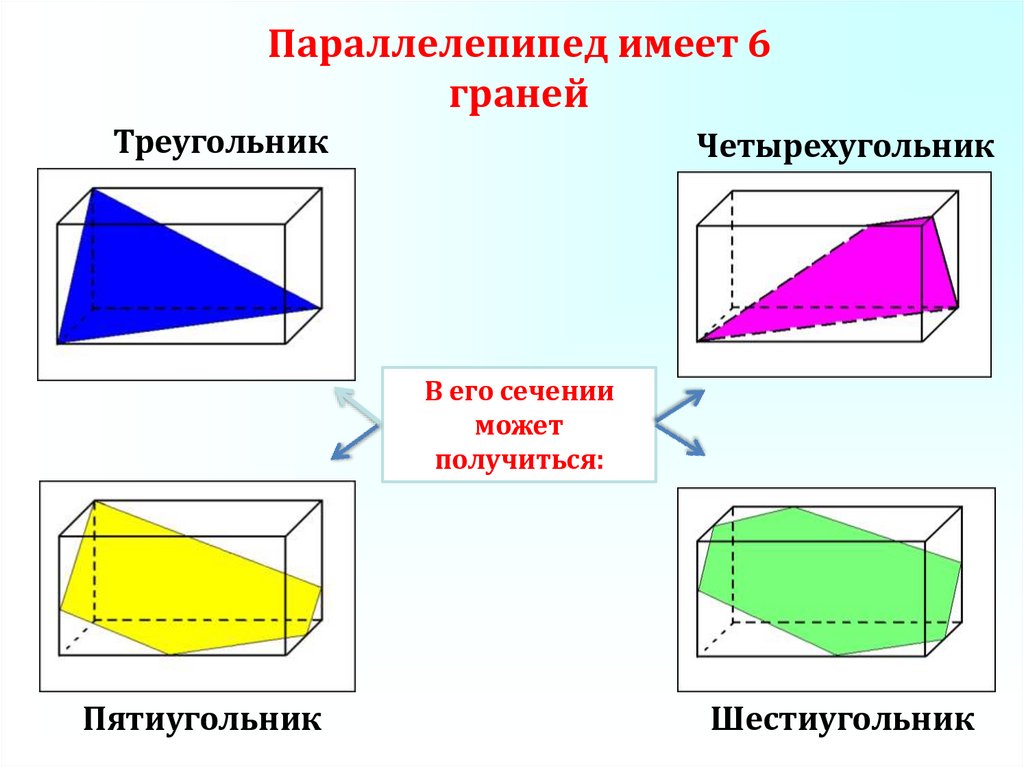
Параллелепипед имеет 6
граней
Треугольник
Четырехугольник
В его сечении
может
получиться:
Пятиугольник
Шестиугольник

27. Параллелепипед имеет 6 граней

Построение сечений
параллелепипеда

28. Построение сечений параллелепипеда

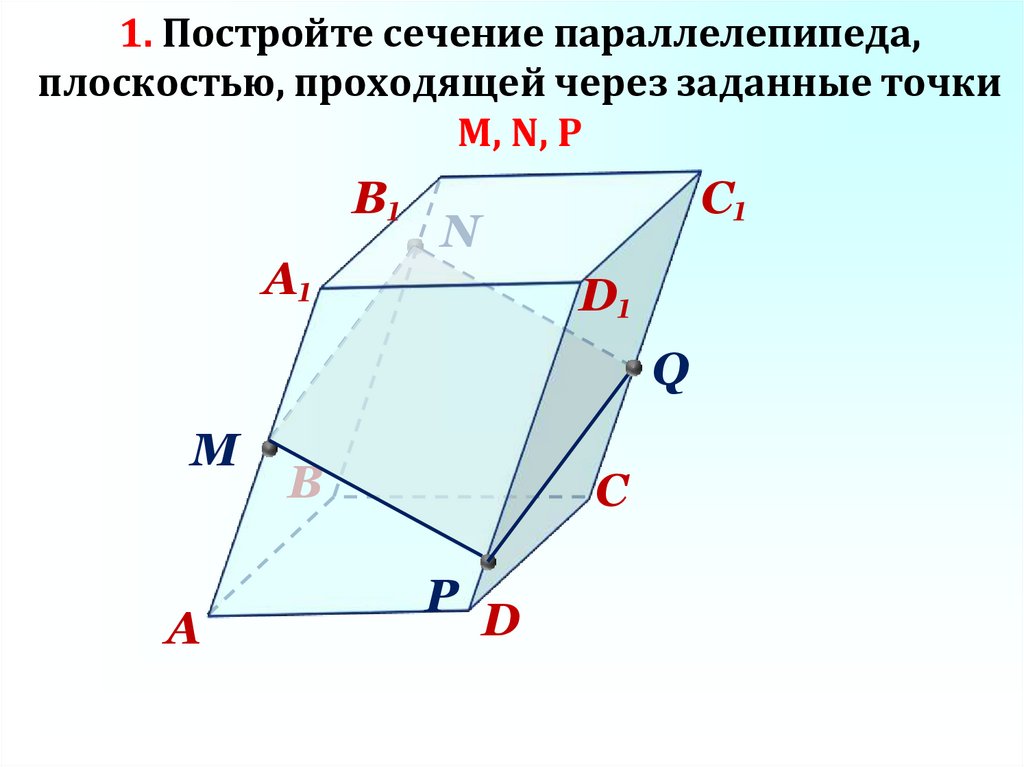
1. Постройте сечение параллелепипеда,
плоскостью, проходящей через заданные точки
M, N, P
B₁
A₁
C₁
N
D₁
Q
М
A
В
C
P
D

29. 1. Постройте сечение параллелепипеда, плоскостью, проходящей через заданные точки M, N, P

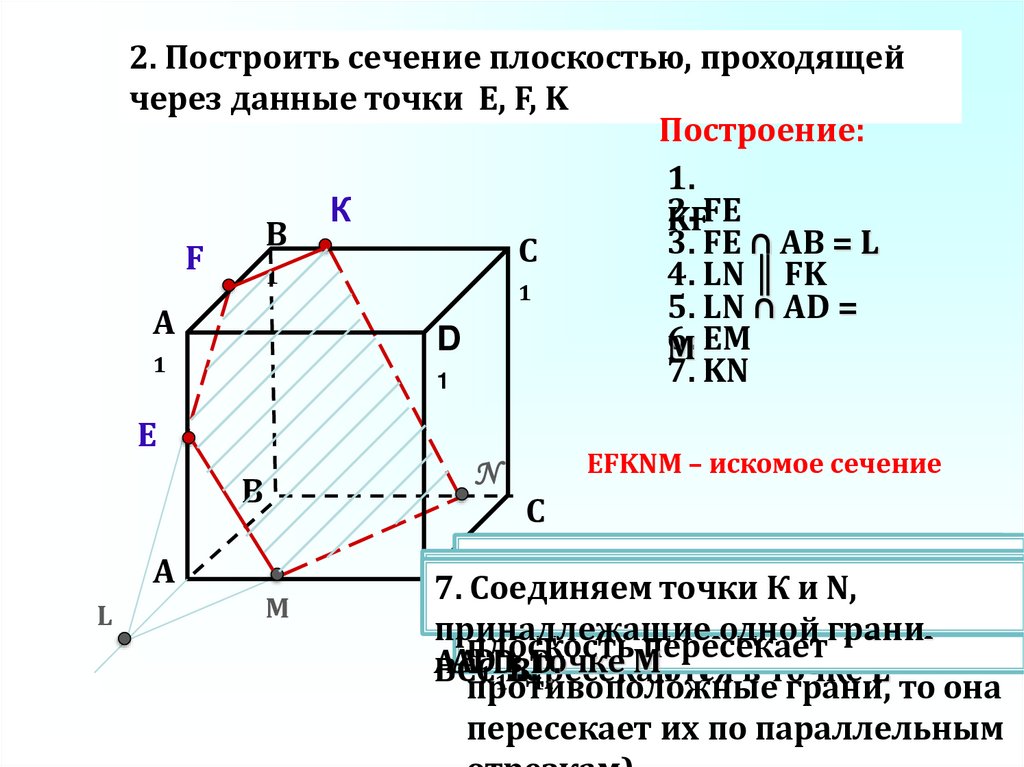
2. Построить сечение плоскостью, проходящей
через данные точки Е, F, K
Построение:
1.
К
2.
FE
KF
В
3. FE ∩ АB = L
C
F
1
4. LN ║ FK
1
5. LN ∩ AD =
А
6.
EM
D
M
1
7. KN
1
E
N
В
А
L
М
EFKNM – искомое сечение
С
4.
1.
Проводим
Соединяем
прямую
точки
K
LN
и E,
F,
6.
Соединяем
2.
Соединяем
точки
точки
Е
и
F
М,
и
7. 3.
Соединяем
Прямые
FE
точки
и
АВ,
Клежащие
и
N,
в
параллельно
принадлежащие
FK
(если
одной
секущая
Dпринадлежащие
5. Прямая
LN пересекает
ребро
принадлежащие
одной
одной
грани
принадлежащие
одной
грани
АА
одной
В
В,
грани
1
1
плоскость
грани
А
пересекает
В1ВС1В.
D1.
1
AD
в
точке
M
АА
D
грани
D.
АА
ВСС
В1 1.
1 1пересекаются
1 1 в точке L
противоположные
грани, то она
пересекает их по параллельным

30.

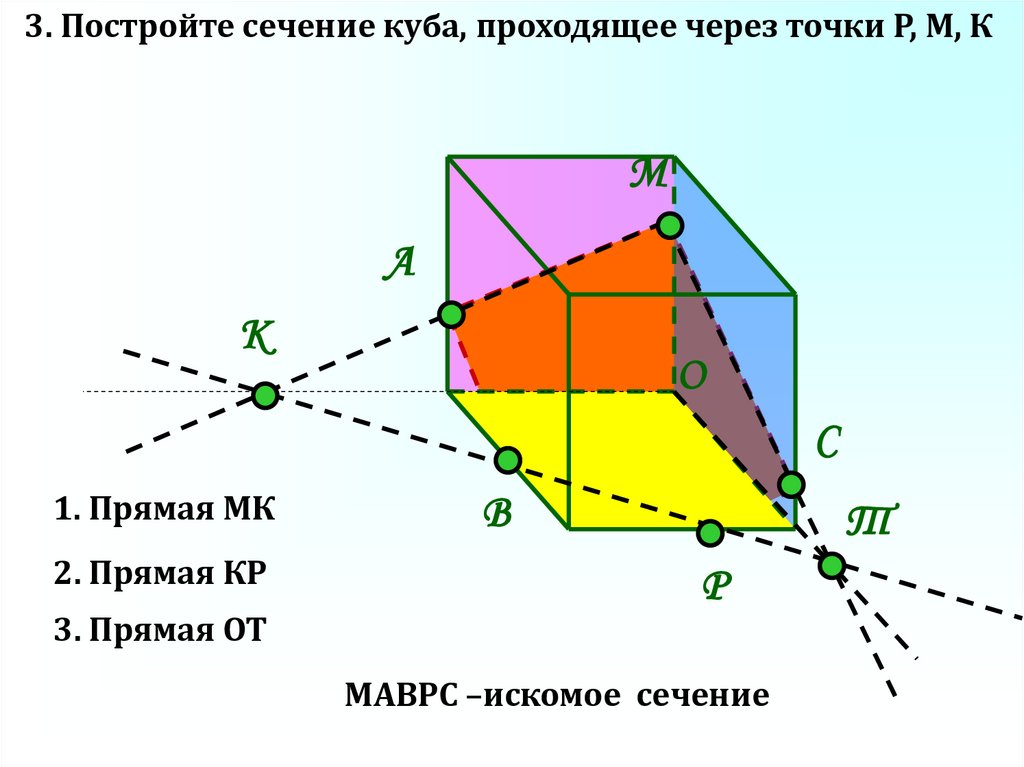
3. Постройте сечение куба, проходящее через точки P, М, К
М
А
К
О
С
1. Прямая МК
2. Прямая КР
3. Прямая ОТ
В
Т
Р
МАВРС –искомое сечение

31.

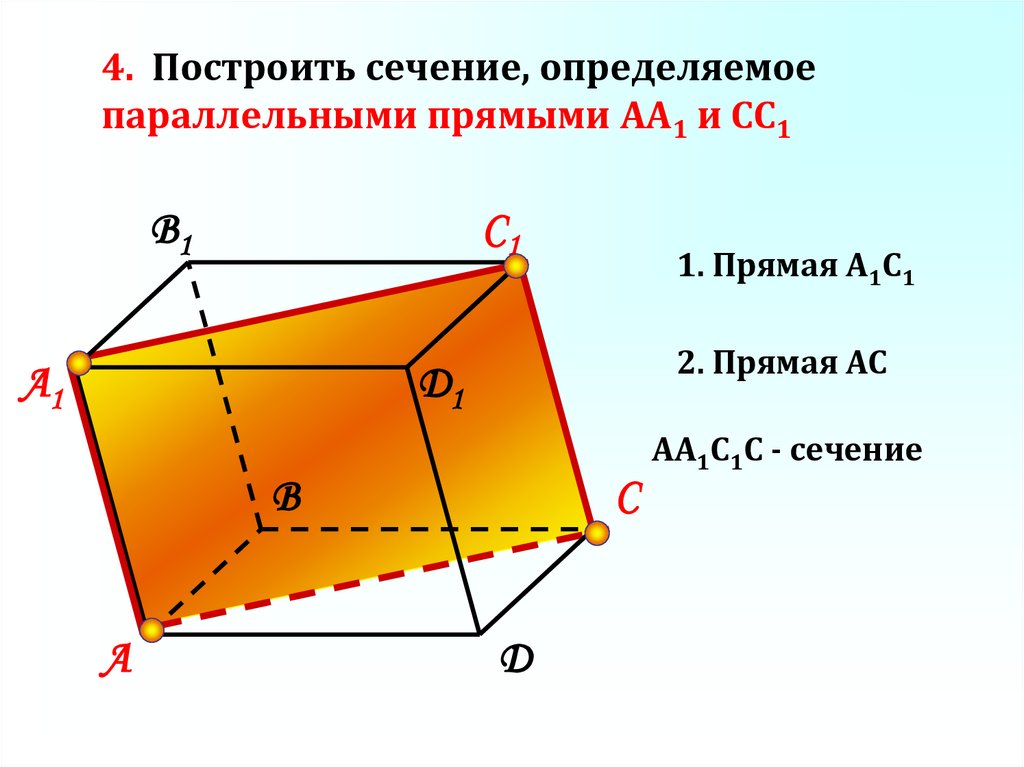
4. Построить сечение, определяемое
параллельными прямыми АА1 и CC1
В1
С1
А1
1. Прямая А1С1
2. Прямая АС
D1
С
В
А
D
АА1С1С - сечение

32.

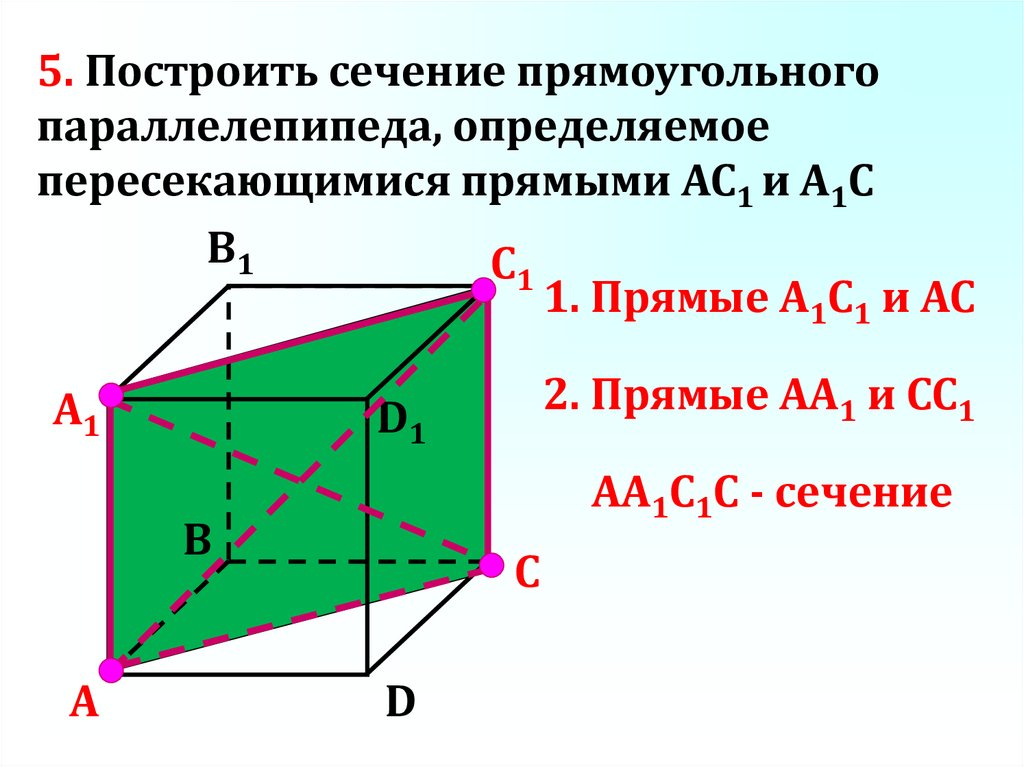
5. Построить сечение прямоугольного
параллелепипеда, определяемое
пересекающимися прямыми АС1 и А1С
В1
С1
1. Прямые А1С1 и АС
А1
D1
АА1С1С - сечение
В
А
2. Прямые АА1 и СС1
С
D

33.

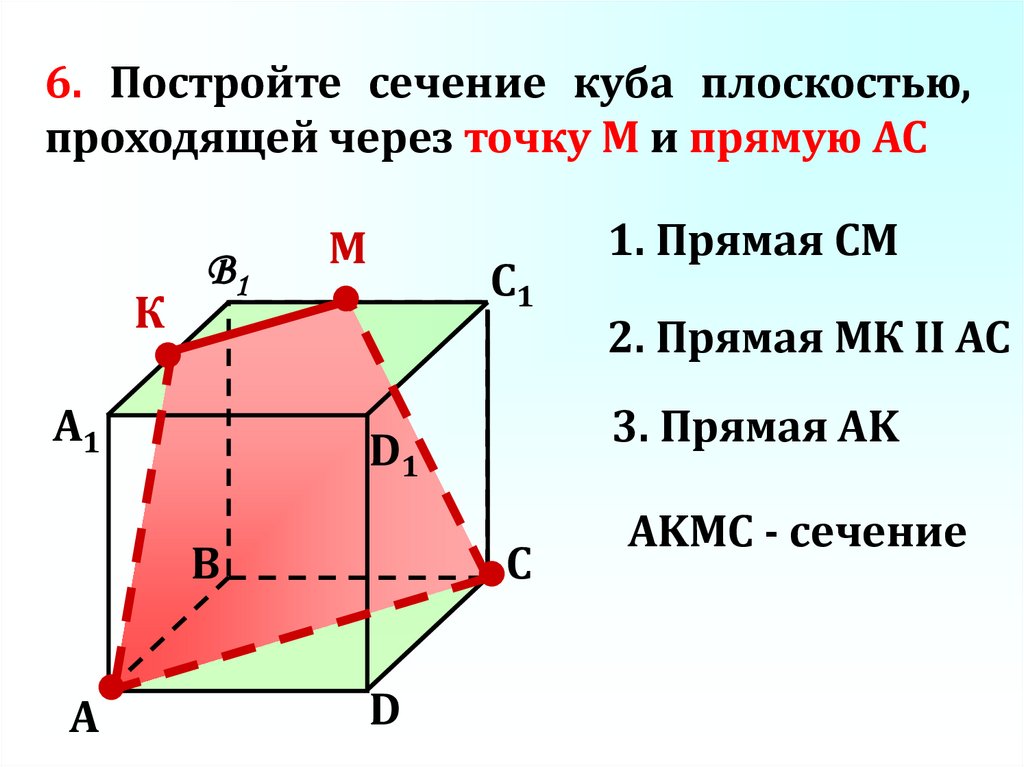
6. Постройте сечение куба плоскостью,
проходящей через точку М и прямую АС
К
В1
А1
М
С1
А
С
D
2. Прямая МК II AC
3. Прямая AK
D1
В
1. Прямая СМ
AKМС - сечение

34.

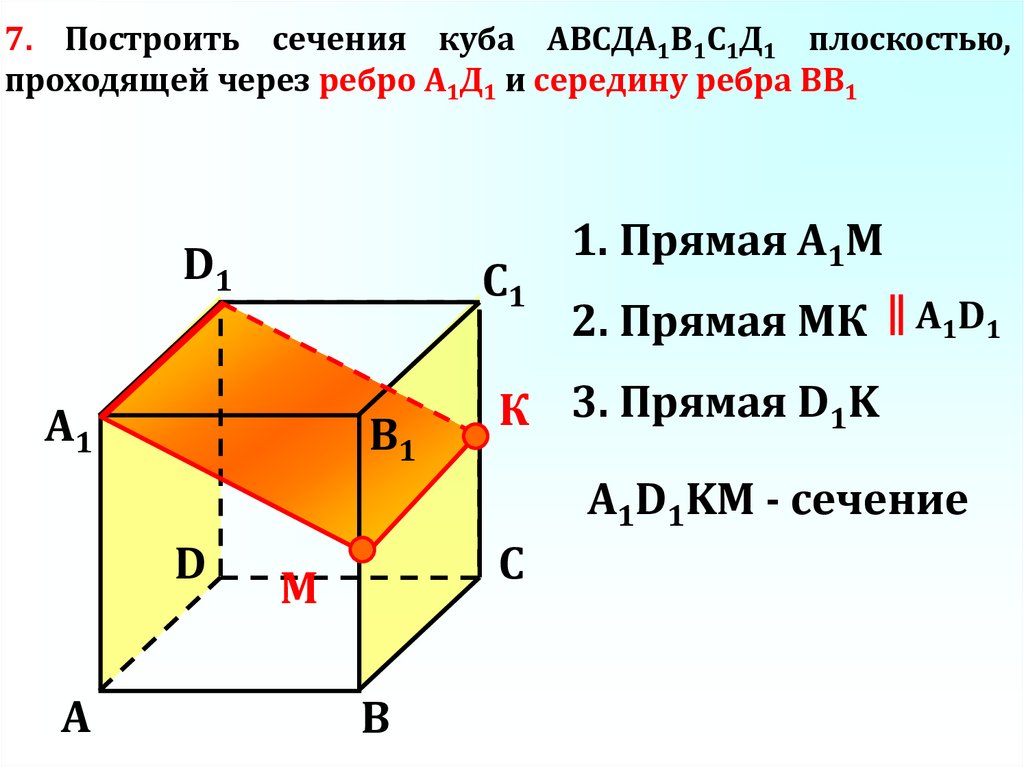
7. Построить сечения куба АВСДА1В1С1Д1 плоскостью,
проходящей через ребро А1Д1 и середину ребра ВВ1
D1
С1
А1
В1
1. Прямая А1М
2. Прямая МК
А1D1
К 3. Прямая D1K
A1D1KM - сечение
D
А
С
М
В

35.

Выводы:
Изучив и проанализировав литературу по теме:
«Построение сечений многогранников»
мы классифицировали задачи с учетом задания
точек сечения параллелепипеда и выяснили:
1. Соединять можно только две точки, лежащие в
плоскости одной грани.
2. Если нет по условию двух точек, лежащих в
плоскости (одной грани многогранника) или одна из
трёх точек находится внутри фигуры или же
снаружи, находясь в пространстве, то сначала надо
построить вспомогательную плоскость, которая
пересекала бы основание данной фигуры или его
продолжение, которая в свою очередь будет
пересекать какие-то стороны основания или их
продолжение.
3. Секущая плоскость пересекает параллельные грани
по параллельным отрезкам.

36. Выводы: Изучив и проанализировав литературу по теме: «Построение сечений многогранников» мы классифицировали задачи с учетом

M
P
M
N
P
M
N
N
P
N
M
N
M
P
N
P
P
M