L15_HydroGaz_2025_12_15

1.

Курс общей физики НИЯУ МИФИ
Основы механики
Лекция 15
Элементы механики сплошных сред
Обзор курса.
Лектор: профессор НИЯУ МИФИ,
Ольчак Андрей Станиславович

2.

Механика жидкостей и газов
1. Механика материальной точки
2. Механика твердого тела
3. Механика жидкостей и газов

3. Механика жидкостей и газов

Что мы знаем из школьного курса физики?
1) На тело, погруженное в газ или жидкость, действует сила Архимеда,
направленная вверх и равная численно весу вытесненной телом жидкости
или газа:
Fарх = ρжgVтела
2) На поверхность тел, погруженных в газ или жидкость, действует сила
гидродинамического давления, пропорциональная площади поверхности
и перпендикулярная ей.
3) Давление атмосферы у поверхности Земли равно Ратм =~ 105 Па
4) На глубине Н под поверхностью жидкости ее давление равно:
Р = ρжgН
5) На тело, движущееся в жидкости или газе, действует сила
сопротивления, направленная против скорости тела (если тело имеет
простую геометрическую форму) и тем большая, чем больше скорость.
Fсопр ~ v или v2

4. Примеры задач

На тело, погруженное в газ или жидкость, действует сила Архимеда,
направленная вверх и равная численно весу вытесненной телом жидкости
или газа:
Fарх = ρжgVтела
1. Два тела равного объема уравновешены на весах. Как изменится
положение рычага весов, если поместить грузы в воду?
ОТВЕТ: Никак
2. …а если поместить в воду только один из грузов?
ОТВЕТ: Другой груз начнет перевешивать
3. …а если объемы тел разные?
Станет перевешивать то, что имеет меньший объем. :

5.

Примеры задач
2) На поверхность тел, погруженных в газ или жидкость, действует сила
гидродинамического давления, пропорциональная площади поверхности
и перпендикулярная ей.
3) Давление атмосферы у поверхности Земли равно Ратм =~ 105 Па
4) На глубине Н под поверхностью жидкости ее давление равно:
Р = ρжgН
ПРИМЕРЫ:
1. «Магдебургские полушария»:
Какую силу надо приложить,
чтобы их разъединить?
F = SРатм , где S - площадь стыка
полушарий
2. Гидравлический пресс,
преобразующий силы
F1/F2 = S1/S2

6. Механика жидкости

Основные понятия и определения
v
dV
1) Частица жидкости - малый объем ее dV,.
Аналог материальной точки.
2) Объем мал по сравнению с областью течения,
но велик по сравнению с межмолекулярными
расстояниями (dV ~1 мкм3).
2) Для каждой частицы жидкости можно указать ее
вектор скорости как функцию времени.
3) Поле векторов скорости: совокупность векторов
скорости для всех точек течения
4) Векторное поле – математическая функция, где каждой точке
пространства сопоставляется вектор. Поле векторов называют
стационарным, если вектора в каждой точке т не меняются со временем.
5) Несжимаемая жидкость, текучая среда, плотность которой ρ во
всех точках течения постоянна и одинакова.

7.

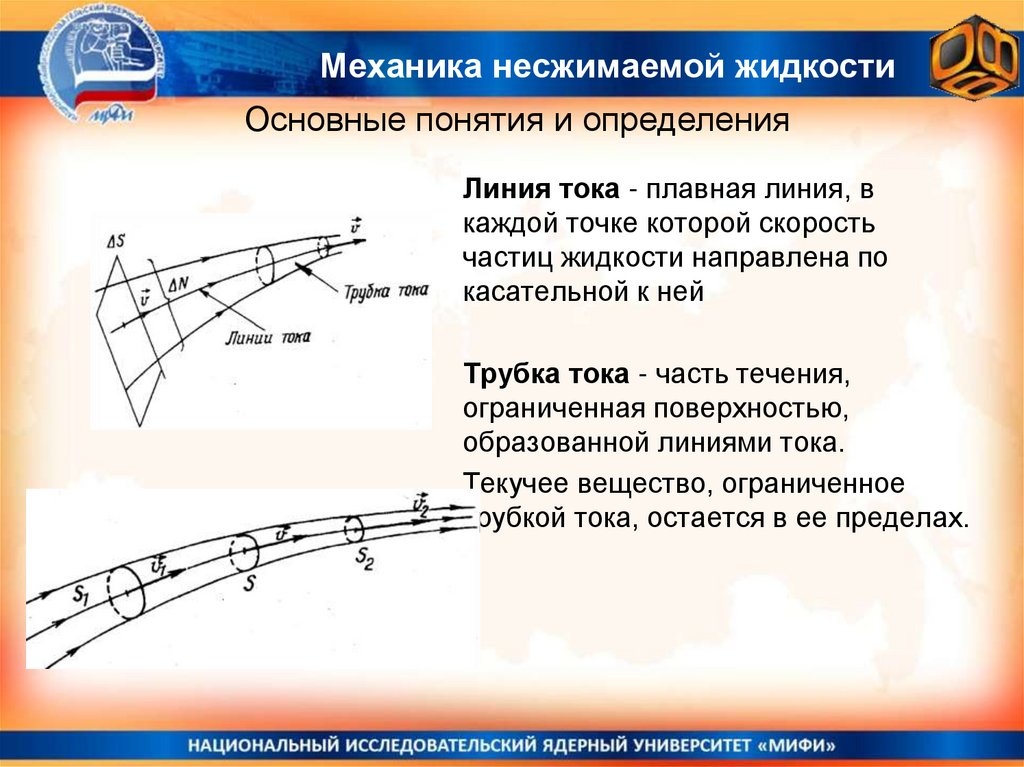
Механика несжимаемой жидкости
Основные понятия и определения
Линия тока - плавная линия, в
каждой точке которой скорость
частиц жидкости направлена по
касательной к ней
Трубка тока - часть течения,
ограниченная поверхностью,
образованной линиями тока.
Текучее вещество, ограниченное
трубкой тока, остается в ее пределах.

8.

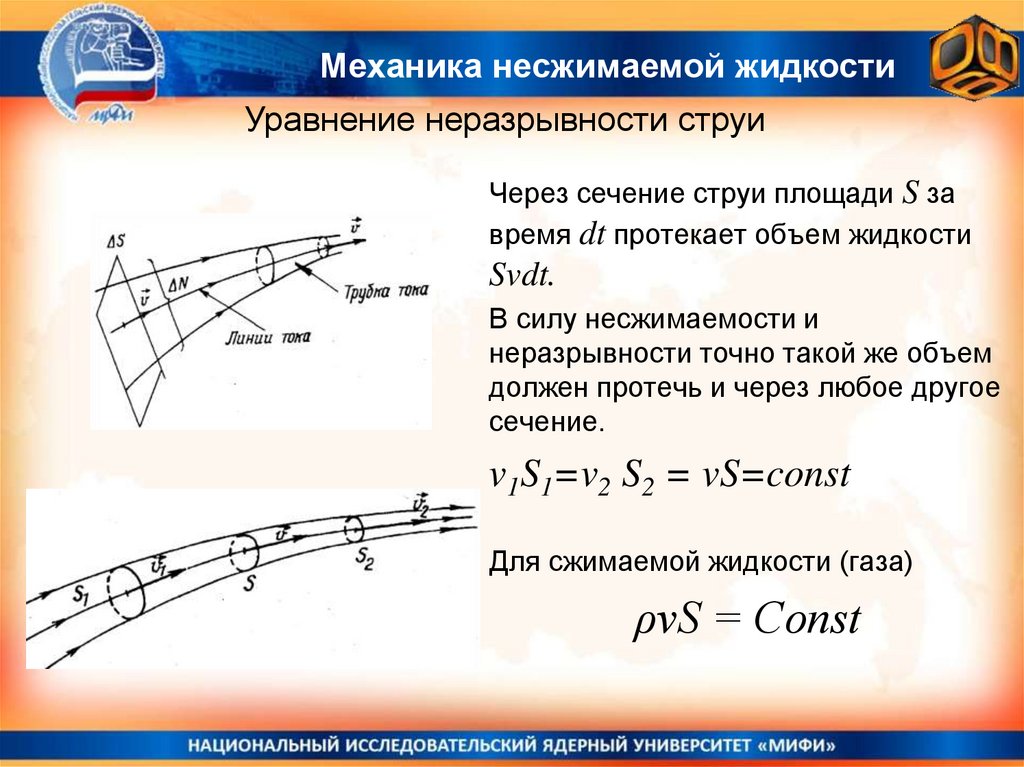
Механика несжимаемой жидкости
Уравнение неразрывности струи
Через сечение струи площади S за
время dt протекает объем жидкости
Svdt.
В силу несжимаемости и
неразрывности точно такой же объем
должен протечь и через любое другое
сечение.
v1S1=v2 S2 = vS=const
Для сжимаемой жидкости (газа)
ρvS = Const

9.

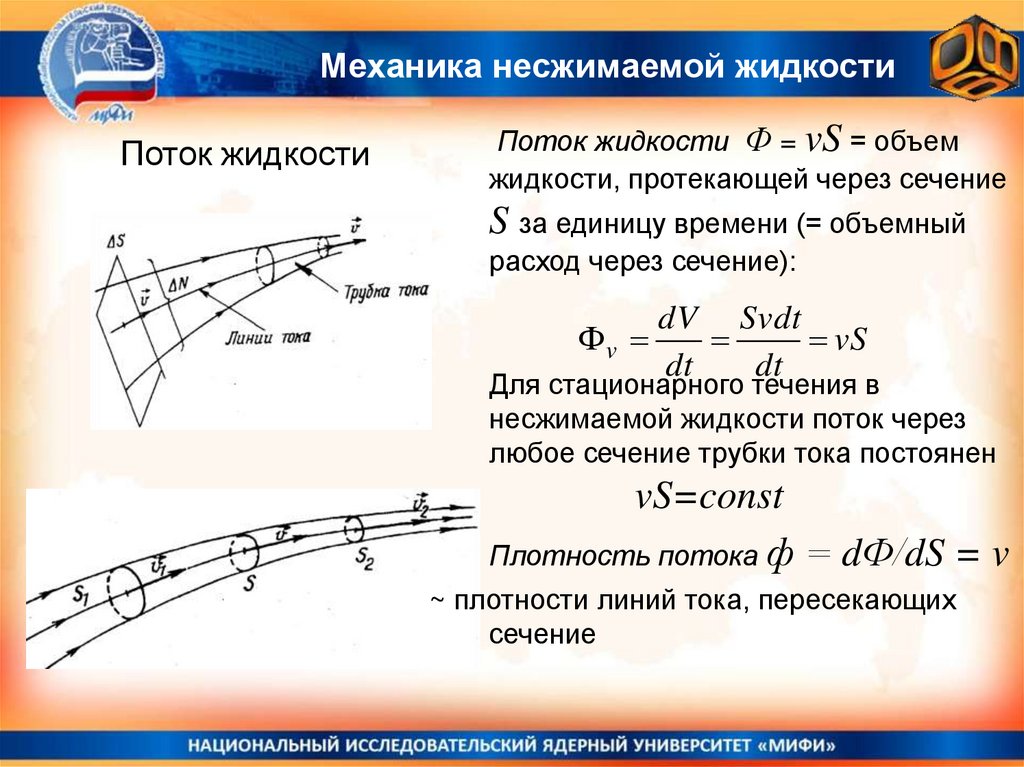
Механика несжимаемой жидкости
Поток жидкости
Поток жидкости Ф = vS = объем
жидкости, протекающей через сечение
S за единицу времени (= объемный
расход через сечение):
dV Svdt
v
vS
dt
dt
Для стационарного течения в
несжимаемой жидкости поток через
любое сечение трубки тока постоянен
vS=const
Плотность потока ф = dФ/dS = v
~ плотности линий тока, пересекающих
сечение

10.

Уравнения Эйлера
Жидкость, в которой отсутствуют
силы трения, называют идеальной.
Для идеальной жидкости
справедливо уравнение Эйлера
dv
P g .
dt
Уравнение Эйлера для идеальной жидкости = аналог второго
закона Ньютона для мат.точки

11.

Уравнения идеальной жидкости
Жидкость, в которой отсутствуют
силы трения, называют идеальной.
Для идеальной жидкости
справедливо уравнение Эйлера
dv
P g .
dt
Умножим уравнение Эйлера скалярно на dr = vdt:
d(ρv2/2) = d(ρ(g,r)) - dp ; g ge z
Интегрируя, получаем уравнение Бернулли:
ρv2/2 +р+ρgz = B, где В - постоянная Бернулли
Вдоль трубки тока величина v 2
2
gz p
остается постоянной

12.

Истечение жидкости из отверстия
Задача: как быстро выльется вода из сосуда
высоты h с основанием S через малое
отверстие у дна площади s.
S
РЕШЕНИЕ: Давление в верхнем (S) и нижнем (s)
сечениях трубки тока равно атмосферному.
Следовательно:
v02 v 2
gh
2
2
v 0 S vs
dh
v0
dt
v
s
- скорость опускания
свободной поверхности
- скорость истечения из отверстия
v = (2gh/(1 - s2/S2))1/2 => v
2 gh
- формула Торричелли
H
dh s
S
S
dh
v0
2 gh =>
dt =>
dt S
s
s 2g
h
0
0
2H
g

13.

Истечение жидкости
Задача о пульверизаторе. .
Давление у входа в трубку
*внизу) – Р0. Скорость потока
газа над трубкой - v. На какую
максимальную высоту
устройство может поднять воду ?
Над трубкой статическое
давление понизится на величину
давления – ρвоздv2/2, что
позволяет скомпенсировать
давление столба воды ρводgh:
ОТВЕТ: h = ρвоздv2/2gρвод

14.

Течения ламинарное и турбулентное
Ламинарное течение – линии
тока не пересекаются.
Ламинарное течение может быть
стабильным и стационарным.
Турбулентное течение: линии
тока завихряются, обрываются,
пересекаются… Течение
нестабильное, нестационарное.
пульсирующее.
Течения воды и воздуха в природе
чаще всего турбулентны

15.

Гидродинамическое подобие
Число Рейнольдсa Re = ρvr/η , определяет характер течения.
r - характерный геометрический размер течения или обтекаемого тела (диаметр
трубы, радиус обтекаемого шарика, толщина крыла и т.п.
η - вязкость среды. Характеризует внутреннее трение в текучей среде и
сопротивление, которое оказывает среда движущимся в ней телам
Re < 1 - течение ламинарное, сопротивление среды Fres ~ v
Re >> 1 - течение турбулентное, сопротивление среды Fres ~ v2
Течения со сходными значениями Re – гидродинамически подобны.

16.

Ламинарное обтекание сферы
F = - 6πηrv
Формула Стокса для силы сопротивления
движению шарообразного тела радиуса r
в жидкости с динамической вязкостью η
ПРИМЕР: скорость устойчиворавномерного падения шарика в
жидкости:
mg = gρ(4/3)πr3 = 6πηrv
v = 2gρr2/9η
Для ламинарного течения можно получить умеренно слождное
дифференциальное уравнение, которым оно описывается

17.

Уравнения Навье - Стокса
dv
Fтр S
dz

18.

Уравнения Навье - Стокса
mw Fi
i
dv
dV
pdV v dV gdV
dt
dv
p v g
dt
ПРИМЕР: с помощью УНС можно, например, рассчитать скорость течения
жидкости c вязкостью η в трубе длины l и радиуса R:
v = R2∆P/4ηl , где ∆P - разность давлений на концах трубы

19.

Что мы будем изучать дальше?
Молекулярная физика и термодинамика. Все тела состоят из
молекул и атомов. Теплота есть проявление энергии движения
составляющих тело молекул и атомов – то есть, внутренняя энергия
системы. Температура = мера ее.
Электродинамика. Взаимодействие микрочастиц материи носит
электро-магнитный характер. Взаимодействие осуществляется
через посредство электрического и магнитного полей, способных
переносить как энергию, так и импульс (электромагнитные
волны).
Квантовая физика: Взаимодействия между частицами в
микромире носят вероятностный (квантовый) характер.
…..Вам предстоит узнать еще много интересного…..
http://www.allposters.com/-sp/Einstein-E-Mc2-Posters_i314174_.htm

20.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!

21.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Удачи на экзаменах!..
…и до встречи в новом семестре…