Похожие презентации:
Основы гидромеханики. Механика жидкости и газа
1.
Основы гидромеханикимеханика жидкости и
газа
Основные понятия и определения
Физические свойства жидкостей
Элементы гидростатики
Элементы гидродинамики
2. Гидромеханика
- наука, изучающая равновесие и движение жидкости, а такжевзаимодействие между жидкостью и твердыми частицами,
погруженными в жидкость полностью или частично.
По принципу целенаправленности гидромеханические процессы
можно разделить на:
1. Процессы перемещения потоков в трубопроводах и аппаратах;
2. Процессы, протекающие с разделением неоднородных систем
(осаждение, фильтрование, центрифугирование)
3. Процессы, протекающие с образованием неоднородных систем
(перемешивание, псевдоожижение и др.)
Законы гидромеханики и их практические приложения изучают в
ГИДРАВЛИКЕ
3.
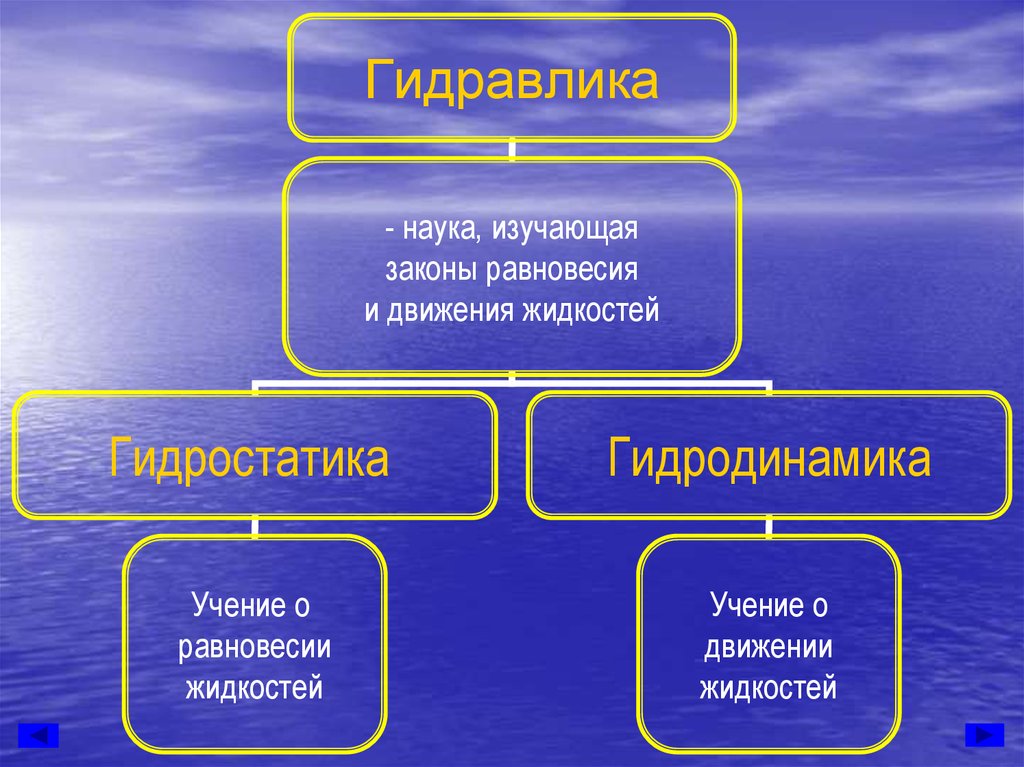
Гидравлика- наука, изучающая
законы равновесия
и движения жидкостей
Гидростатика
Гидродинамика
Учение о
равновесии
жидкостей
Учение о
движении
жидкостей
4.
- физические тела, которые легко изменяют своюформу под действием приложенных сил.
Капельные
Газообразные
характеризуются малой сжимаемостью и
относительно небольшим изменением объема при
изменении температуры.
5.
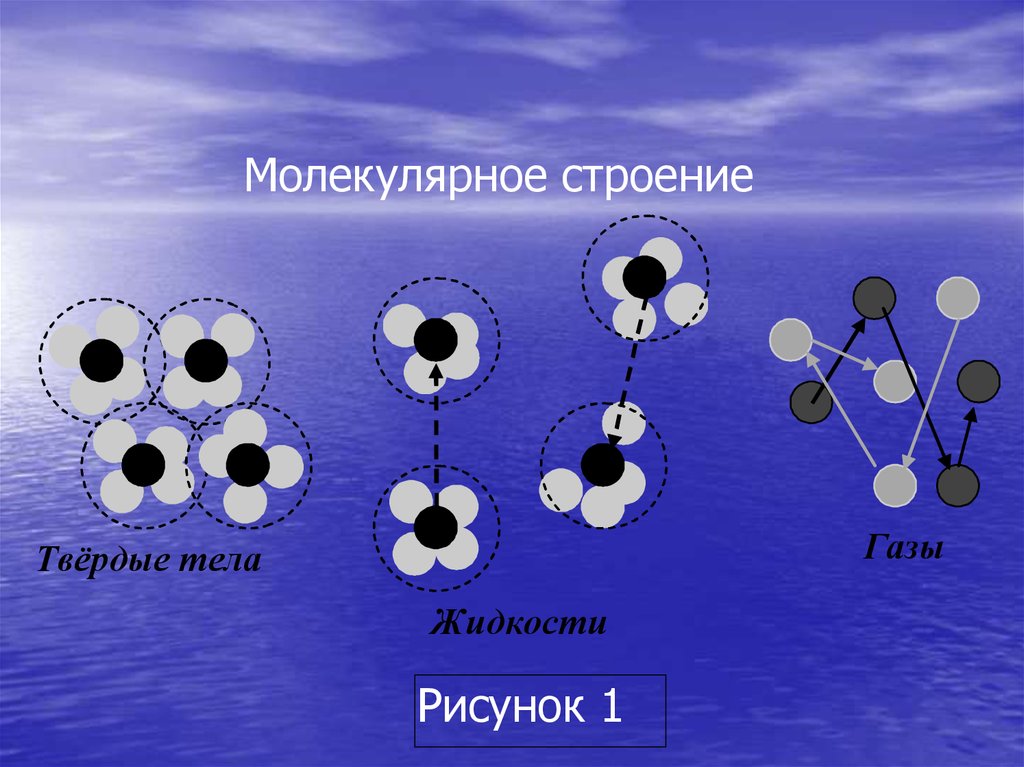
Молекулярное строениеГазы
Твёрдые тела
Жидкости
Рисунок 1
6.
Предмет гидравлики• Гидравлика– наука о движении и покое
воды и других жидкостей. Жидкость в
гидравлике представляют как сплошную
среду, легко изменяющую форму под
действием внешних сил.
• Сплошная среда– это масса, физические и
механические параметры которой являются
функциями координат в выбранной системе
отсчета. Молекулярное строение жидкостей
заменяется сплошной средой той же массы.
7.
Понятие жидкости.Свойства капельной,
некапельной и идеальной жидкости
Жидкостью называется физическое тело,
обладающее текучестью и не имеющее своей
формы, но принимающее форму того сосуда, в
котором оно находится.
Текучестью называется способность жидкости
изменять свою форму, не дробясь на части,
под действием даже небольших сил.
8.
Различают два вида жидкостей:капельные и некапельные (газообразные).
Капельные жидкости: оказывают большое
сопротивление изменению объема и
трудно поддаются сжатию.
• При изменении давления и температуры их
объем изменяется весьма незначительно.
• Любая капельная жидкость может переходить в газообразное состояние при
определенной температуре и давлении.
• Практически не оказывают заметного
сопротивления растягивающим усилиям.
• Оказывают существенное сопротивление
сдвигающим силам.
9.
Некапельные (газообразные) жидкости• Изменяют свой объем в зависимости от этих
же факторов в значительной степени.
• При понижении температуры и повышении
давления могут переходить в жидкое
состояние.
Идеальная жидкость — это жидкость, лишен-
ная вязкости ( = 0). Эту модель используют для
упрощения расчетов в случае, когда силами вязкости
можно пренебречь.
10.
• Физические свойства жидкости1 – Плотность
m
lim
V 0 V
кг
м
3
р, Т
pV nRT ; n m M
p
R0T ;
R0 R
M R 8,314 кДж кмоль
2 – Сжимаемость жидкости
определяется производной р/ ,
11.
Несмотря на значительную сжимаемость газов посравнению с жидкостями при скоростях в средах
v<0,1с (с — скорость звука в среде), при решении
конкретных задач сжимаемостью можно пренебречь.
Поэтому понятие “несжимаемая жидкость” нашло
широкое применение.
V
V p p
p
E0 1
p
p
E0
c
c k c
свозд=330 м/с; свод=1414 м/с; Ма=u/c
скорость распространения малых возмущений
давления в данной среде,
12.
ВЯЗКОСТЬ ИЛИ ВНУТРЕННЕЕТРЕНИЕ В ЖИДКОСТЯХ
Характеризует ее способность сопротивляться
сдвиговым усилиям.
z, м
F
u0
F = Su0/
x, м
u, м/c
du
dz
13.
где μ – коэффициент пропорциональности илидинамический коэффициент вязкости.
Единица измерения – Па с; Пуаз (П):
1 П = 0,1 Па·с; 1 Па с = 1 сП
На практике чаще используется
кинематический коэффициент вязкости
14.
01
2
3
3
du
.
dz
ньютоновская (вода, керосин, спирт, газы)
4
du/dz
1
du
0
.
dz
вязкопластическая или бингамовская (глинистые и цементные р- ры; пасты; пена;
масл. краски)
n
2, 4
du
C .
dz
2 – псевдопластическая (суспензии из
ассим. част.; р-ры полимеров; еллюлоза);
4 – дилатантная ( клейстер, крахмал)
1 – масло; 2 – воздух; 3
– керосин; 4 – водород;
5 – вода
15.
Вязкость жидкости определяется экспериментально спомощью приборов, которые называются
вискозиметрами. Примером такого прибора может
служить вискозиметр Стокса.
G шWg ,
A
v
Шарик
FC
G
A жWg ,
FC 3 v
2
1
2 1
g ш ж
18
v
16.
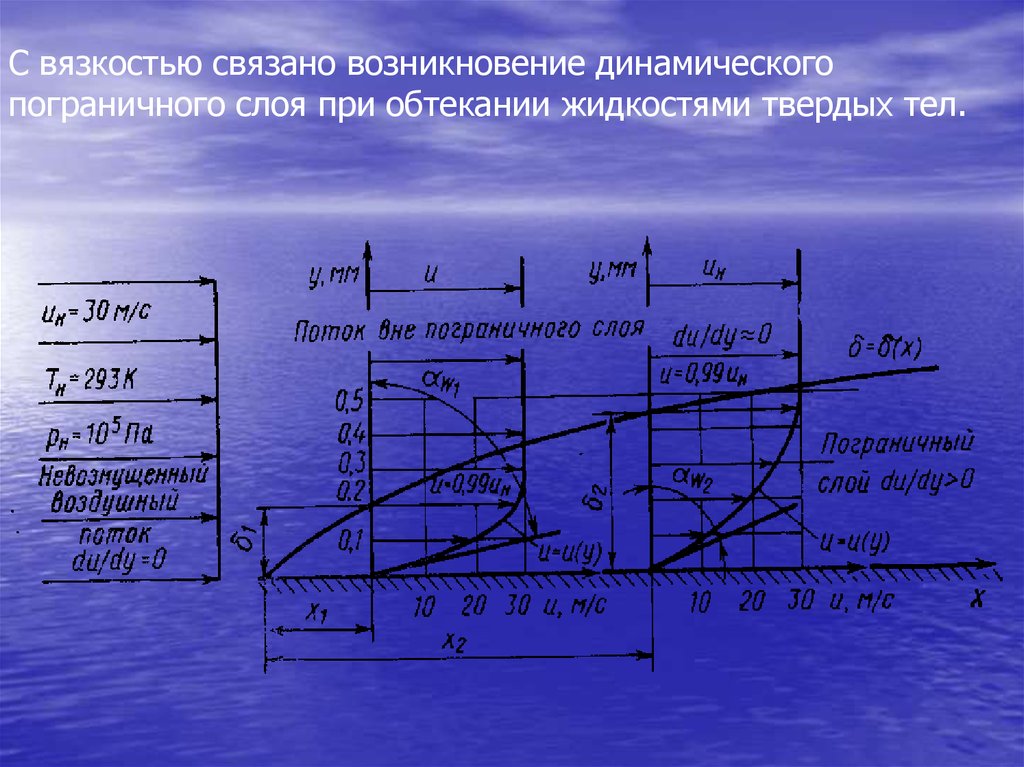
С вязкостью связано возникновение динамическогопограничного слоя при обтекании жидкостями твердых тел.
17.
18.
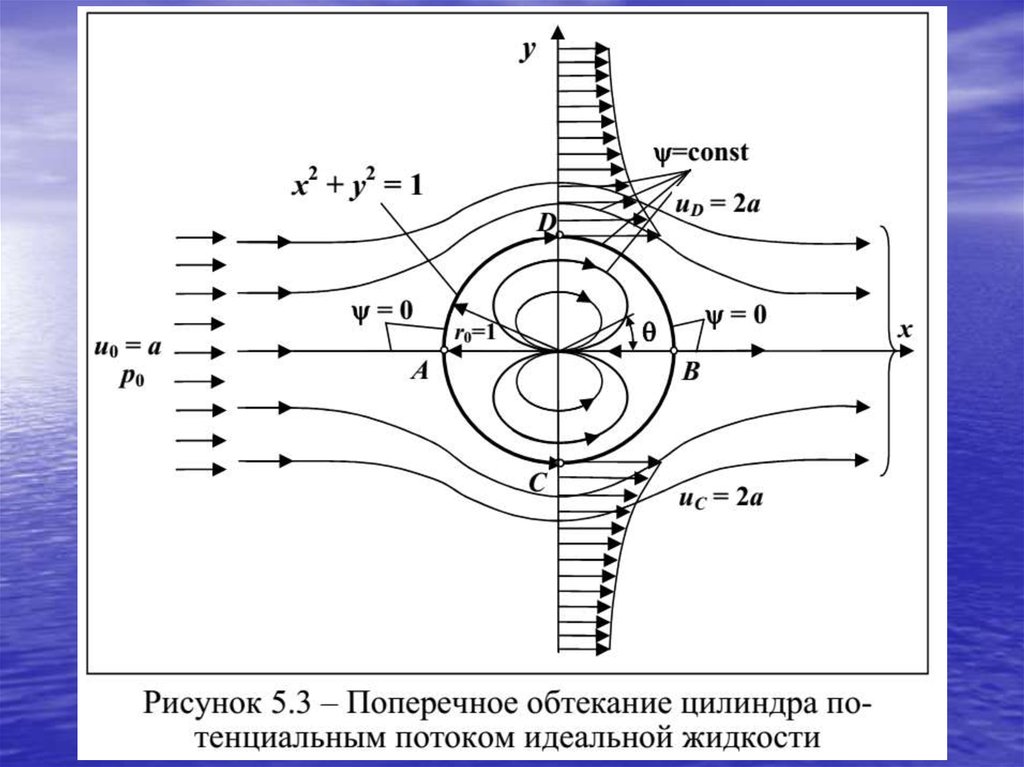
Парадокс ДаламбераВ силу полной симметрии распределения давления по поверхности
цилиндра равнодействующая сил
давления равна нулю. Полученный
вы-вод называется парадоксом
Даламбера: при дозвуковом
безотрывном обтекании тел
идеальной жидкостью сила
лобового сопротивления равна
нулю: сила трения отсутствует, а
вторая составляющая — сила
сопротивления давления,
действующая на переднюю часть
цилиндра, уравновешивается силой
давления на кормовую часть.
Парадокс состоит в несоответствии
этого вывода с
экспериментальными данными —
при обтекании тел реальными
жидкостями всегда возникает сила
19.
Поверхностное натяжениеКоэффициент поверхностного натяжения – , Н/м.
Физический смысл – это свободная потенциальная энергия
единицы поверхности раздела , обусловленная действием сил
притяжения на молекулы вблизи поверхности раздела
Капиллярные явления
На поверхности раздела трех фаз:
твердой стенки, жидкости и газа
образуется краевой угол θ. Величина
угла зависит только от природы
соприкасающихся сред, и не зависит от
формы сосуда и силы тяжести.
1
1
4
p p
d
R1 R2
20.
Давление насыщенных паров рнХарактеризует испаряемость жидкостей. Зависит от температуры Т. Эта
величина определяет то минимальное абсолютное давление, при
котором жидкость не теряет своей сплошности.
местное нарушение сплошности течения с образованием паровых и
газовых пузырей (каверн), обусловленное местным падением давления в
потоке, называется кавитацией.
Кавитация сопровождается характерным шумом, а при длительном её
воздействии также и эрозионным разрушением твёрдых, как
правило, металлических стенок. Последнее объясняется тем, что
конденсация пузырьков пара (и сжатие пузырьков газа) происходит со
значительной скоростью, частицы жидкости, заполняющие полость
конденсирующегося пузырька, устремляются к его центру и в момент
завершения конденсации вызывают местный гидравлический удар, т. е.
значительное местное повышение давления. Разрушение материала при
кавитации происходит не там, где выделяются пузырьки, а там, где они
конденсируются вследствие длительного воздействия знакопеременных
сил.
Кавитация в обычных случаях явление нежелательное.
При кавитации также возрастает сопротивление трубопроводов и,
следовательно, уменьшается их пропускная способность.
21.
ЭЛЕМЕНТЫ КИНЕМАТИКИ ЖИДКОСТИМетод Эйлера заключается в непосредственном
описании поля скоростей в пространстве и
времени, т. е.
u u r , t
или ux=ux(x,y,z,t); uy=uy(x,y,z,t); и= uz(x, у, z, t)
Если u/ t = 0 или, иначе, u = u(x, y, z), то движение
называют установившемся или стационарным
z
Если u/ t 0, то неустановившемся или нестационарным
22.
Линия тока — это линия, в каждой точке которой вданный момент времени вектор скорости u
направлен по касательной, т. е.
u dr u dr 0
u dz u dy i u dx u dz j u dy u dx k 0
y
z
z
x
x
y
dx dy dz
ux u y uz
Траектория– кривая, вдоль которой происходит
перемещение частицы жидкости, т. е.
dr udt dx u x dt ; dy u y dt ; dz u z dt
dx dy dz
dt
ux u y uz
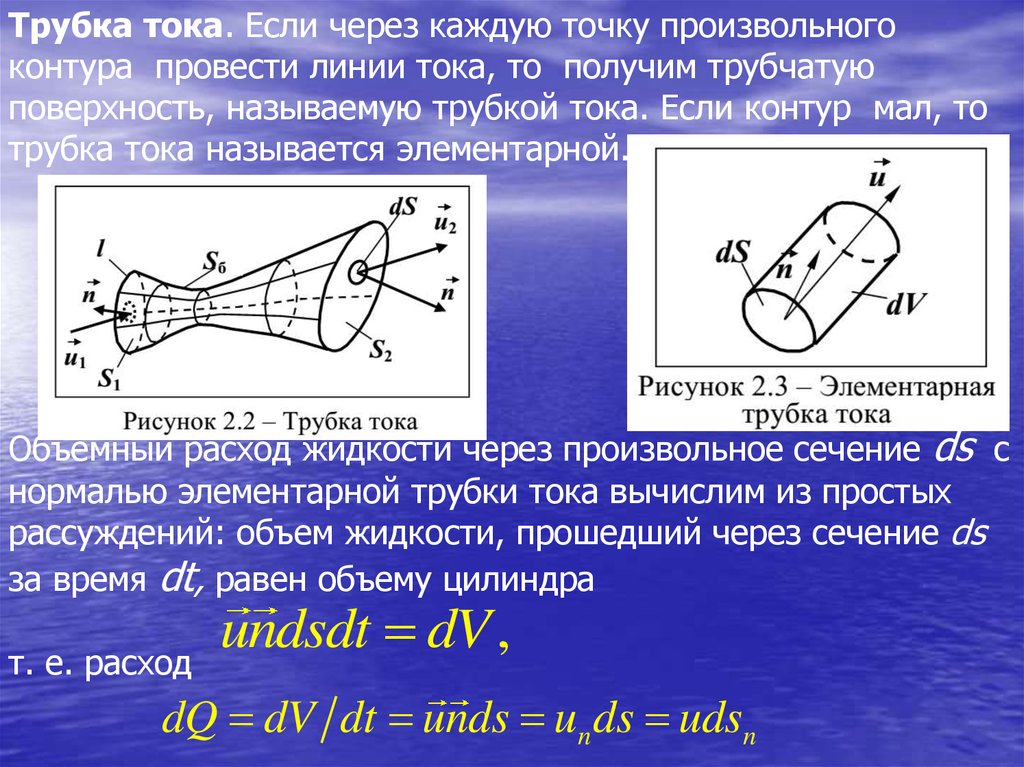
23.
Трубка тока. Если через каждую точку произвольногоконтура провеcти линии тока, то получим трубчатую
поверхность, называемую трубкой тока. Если контур мал, то
трубка тока называется элементарной.
Объемный расход жидкости через произвольное сечение ds с
нормалью элементарной трубки тока вычислим из простых
рассуждений: объем жидкости, прошедший через сечение ds
за время dt, равен объему цилиндра
т. е. расход
undsdt dV ,
dQ dV dt unds un ds udsn
24.
dsn ds cos u, nплощадь сечения, перпендикулярная линиям тока, или
«живое сечение»
dG unds un ds udsn
Объемный и массовый расходы жидкости через произвольную
площадку s найдем, просуммировав расходы по
элементарным пронизывающим ее трубкам, т. е. объемный
расход
Q un ds
G un ds
s
s
Средняя расходная скорость
v в живом сечении sn
υ Q Sn
25.
Ускорение при движении жидкостиdu u dx u dy u dz u
a
dt x dt y dt z dt t
du
u
u
u u
a
ux
uy
uz
dt
x
y
z t
dux
ux
ux
ux ux
ax
ux
uy
uz
dt
x
y
z
t
du
a
dt
26.
Уравнение неразрывностиэто уравнение материального баланса
или иначе закон сохранения массы
Если в сплошной среде выделить
произвольный объем V , то очевидно
m dV
V
m
dV dV
t t V
t
V
Возможно лишь за счет притока жидкости, который равен
суммарному массовому расходу жидкости через поверхность s
объема V, т. е.
27.
G un dss
Тогда
V t dV s un ds 0
уравнение неразрывности в интегральной форме
С учетом теоремы о кратных интегралах
(теоремы Остроградского-Гаусса) можно записать
V t div u dV 0
Поскольку предел интегрирования произволен, то
div u 0
t
28.
Для несжимаемой жидкости =const и0
t
Тогда
u x u y u z
divu
0
x
y
z
Для потока несжимаемой жидкости уравнение неразрывности
для трубки тока с учетом непроницаемости ее боковой
поверхности после интегрирования преобразуется к виду
Q υ1s1 υ2 s2
29.
Скорость деформации30.
uu
u
uB u A du u A dx dy dz
x
y
z
Различие в скоростях обусловлено:
а) растяжением жидкостного элемента, т. е. линейной
деформацией; б) угловой деформацией, изменяющей форму и
размер жидкостной частицы; в) вращением элемента без
деформации. Следовательно, различие в скоростях –
результат деформации жидкостного элемента, т. е.
duдеф du duвр
31.
В свою очередьduвр dr x i y j z k dxi dyj dzk
y dz z dy i z dx x dz j x dy y dx k
32.
Проектируя, например, на ось х будем иметьduдеф x dux duвр y
(1)
ux
ux
ux
dux
dx
dy
dz
x
y
z
(2)
duвр x y dz z dy
(3)
33.
Подставляя (2) – (3) в (1) получимduдеф x
u y
ux
u z
dx
dy
dz y dz z dy
x
y
z
d вр y
то
1
1 ux uz
d A d C
dt
2
2 z
x
y
d вр y
dt
1 ux uz
2 z
x
По аналогии для z можно записать
1 u y ux
z
2 x
y
(4)
34.
Подставляя эти выражения в (4), после преобразований будемиметь
duдеф x xx dx xy dy xz dz
Здесь хх – скорость линейной относительной деформации;
ху; хz – скорости угловой деформации, представляющие
собой
ux
1 ux u y
1 ux uz
xx
; xy
.
; xz
x
2 y
x
2 z
x
Физический (кинематический) смысл
u x
x
35.
В системе координат, связанной с точкой 0 жидкости, завремя dt точка А переместится и займет положение А . Тогда
удлинение отрезка АА1=(uАх—uОх)dt и, так как для бесконечно
малого отрезка 0А
ux
u Ax uOx
0 A , то
x
ux
AA1
0 Adt
x
AA1 ux
xx
0Adt x
По аналогии можно записать
u y
uz
yy
; zz
y
z
36.
Тогда уравнение неразрывности для несжимаемой жидкости,представленное в виде
divu xx yy zz 0
свидетельствует о неизменности объема элемента жидкости
при его линейной деформации
37.
38.
39.
40.
41.
По аналогии можно записать1 ux u y
1 u y uz
xy
; yz
2 y
x
2 z
y
Таким образом имеем
duдеф y yx dx yy dy yz dz; duдеф z zx dx zy dy zz dz
Матрица, составленная из девяти компонентов скоростей
линейных и угловых деформаций называется тензором
скоростей деформаций S.
xx
xy
xz
S yx
zx
yy
zy
yz
zz
42.
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЖИДКИЙ ОБЪЕМВнешние силы, действующие на жидкий объем и
определяющие его движение, разделяются на
массовые (объемные) и поверхностные.
Массовые силы Rm приложены ко всем жидким
частицам, составляющим жидкий объем. К ним
относятся силы тяжести и силы инерции.
Напряжением или плотностью, или удельной
(единичной) массовой силой (м/с2, Н/кг) называют
R mm
f lim
; f a
m 0 m
f f xi f y j f z k ; f z g
43.
Поверхностные силы Rs представляют воздействиевнешней среды на поверхность выделенного объема.
Это воздействие распределено по поверхности
непрерывно.
Выберем на плоскости S, рассекающей нeкотоpyю
массу жидкости на части 1 и 2 (рис. 3.1),
элементарную площадку S, на которой лежит точка
А (х, у, z). Отбросим часть 2 и заменим ее действие
на площадку S части 1 равнодействующей
поверхностных сил Rs. В общем случае величина
Rs зависит от ориентации площадки S и направлена к ней под острым углом у. Ориентация
площадки S определяется единичным вектором
внешней нормали n.
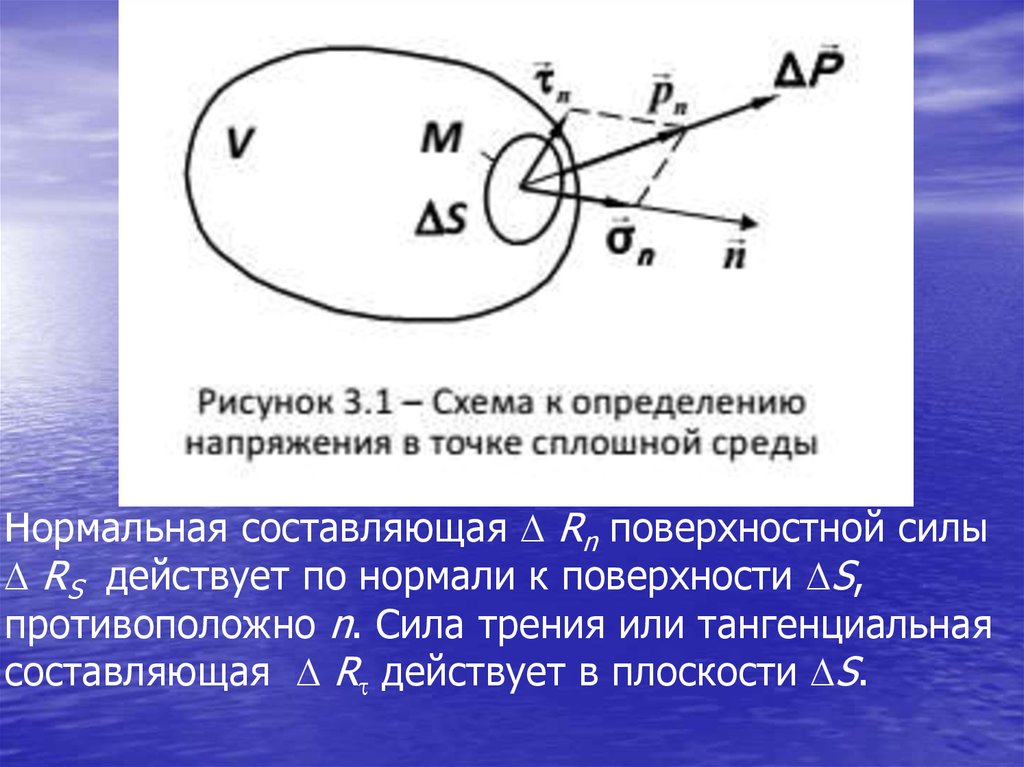
44.
Рисунок 1.1Нормальная составляющая Rn поверхностной силы
RS действует по нормали к поверхности S,
противоположно n. Сила трения или тангенциальная
составляющая R действует в плоскости S.
45.
Плотность поверхностных сил на площадке с нормалью n называется напряжением и определяетсявыражением
RS
pn lim
;
S 0 S
Н
pn 2 Па
м
При этом различают следующие напряжения.
pn pnn n pn
Компоненты напряжения на площадках, нормальных
к координатным осям, называются основными. Так,
например, напряжение на площадке с нормалью,
совпадающей с направлением оси х, может быть
выражено через основные компоненты напряжения в
виде
px xi xy j xz k
46.
Первый индекс указывает направление нормали к площадке,второй – ось, на которую спроектировано напряжение .
Компонент напряжения, считается положительным, если его
направление и направление внешней нормали к площадке
совпадают (или оба направления не совпадают) с
направлениями осей координат. На рисунке 3.2 показаны
положительные направления компонентов напряжения при
плоском напряженном состоянии.
47.
48.
49.
50.
51.
Давление в покоящейся жидкостиp = pn= x= y= z
52.
Закон внутреннего трения в обобщеннойформе – это эмпирический закон
Устанавливает взаимосвязь между компонентами
тензоров скоростей деформаций S и напряжений Т .
Если Т представить в виде
53.
T T0 T1p
0
0
T0 0
p
0
0
0
p
T1
x p
xy
xz
yx
y p
yz
zx
zy
x p
то простейшая форма связи между матрицами S
и Т1 для ньютоновской жидкости – это прямая
пропорциональность
T1 2 S
54.
u x u yu x
x p 2
; xy
;
x
x
y
u y
u y u z
y p 2
; yz
;
y
y
z
u z
u z u x
z p 2
; zx
.
z
z
x
55.
56.
du xx yx zx
X
dt
x
y
z
du y
xy y zy
Y
dt
x
y
z
du z
xz yz z
Z
dt
x
y
z
57.
Уравнение движения вязкойнесжимаемой жидкости
(уравнение Навье—Стокса)
du x
1 p
2
X
u x
dt
x
du y
1 p
2
Y
u y
dt
y
du z
1 p
2
Z
u z
dt
z
2 2 2
x
y
z
2
2
2
2
58.
du1
2
F gradp u
dt
u uxi u y j uz k
F Xi Yj Zk
p p
p
gradp i j k
x
y
z
59.
Уравнение энергииИзменение энергии Е жидкости в случае отсутствия теплообмена с окружающей средой dQ = 0
возможно лишь за счет работы внешних сил, т. е.
dE = dA = Ndt
или иначе
dE
N
dt
Для гомогенной жидкости, не изменяющей своего
агрегатного состояния, можно записать
60.
2u
E dV c pT dV
2
V
V
dE d u 2
dT
du
c pT dV u
cp
dt dt V 2
dt
dt
V
N=Nm+Ns
dV
N m uF dV
V
upx up y up
z
N S upds
dV
x
y
z
V
V
61.
dudT
px p y pz
c p
u
F
dt
x
y
z
dt
u y
u x
u z
px
py
pz
0
x
y
z
u y
dT
u x
u z
u x
c p
x
xy
xz
yx
dt
x
x
x
y
u y
u y
u z
u x
u z
y
yz
zx
zy
z
y
y
z
z
z
62.
dTс р
D
dt
u 2 u y 2 u 2
z
D 2 x
x y z
u x u y u y u z u z u x
x z
y x
z
y
2
2
D 2
2
xx
2
yy
2
zz
4
2
xy
2
xz
2
yz
2
63.
Потери энергии на сопротивлениях и по длинетрубопровода
1
dT
1
hw
c p
dV
DdV
gQ V
dt
gQ V
v2
l v2
4S
hw hмс hl ; hмс ; hl
; dэ
.
2g
dэ 2 g
A
геометрических размеров, Re кв
Re
кв
Reкв
Re
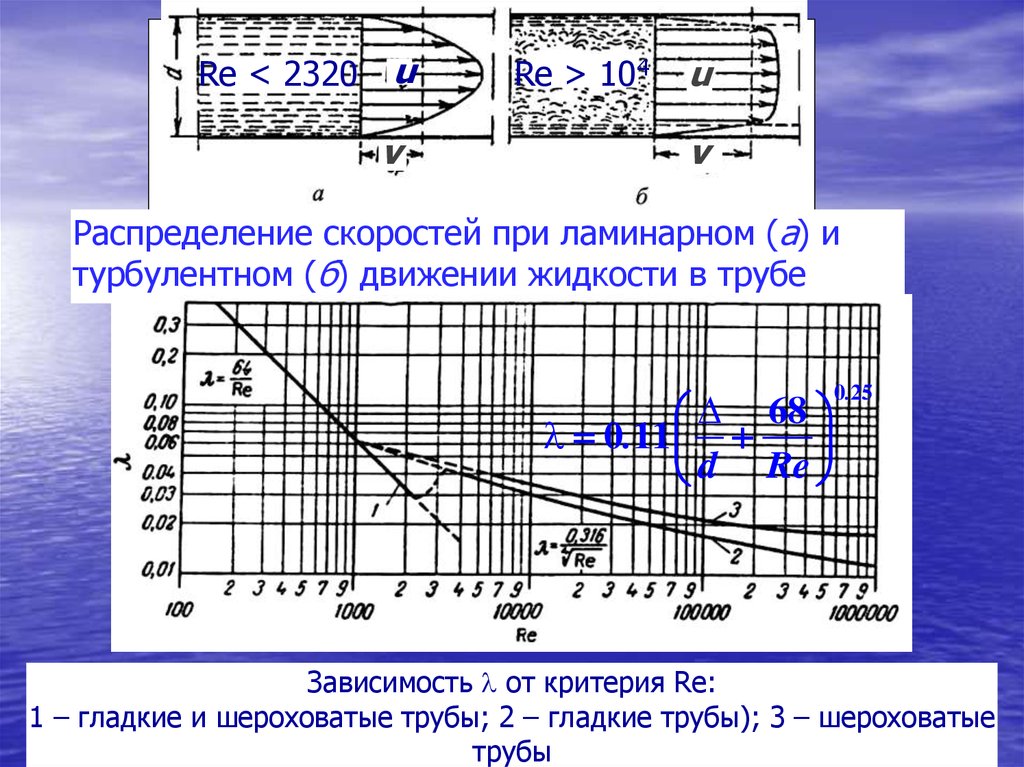
64.
Re < 2320u
v
Re > 104
u
v
Распределение скоростей при ламинарном (а) и
турбулентном (б) движении жидкости в трубе
68
0.11
d Re
0.25
Зависимость от критерия Re:
1 – гладкие и шероховатые трубы; 2 – гладкие трубы); 3 – шероховатые
трубы
65.
ГИДРОСТАТИКА1
F gradp
1 p
fx
x
1 p
fy
y
1 p
fz
z
1 p
p
p
f x dx f y dy f z dz dx dy dz
x
y
z
66.
Если =const, тоp
f x dx f y dy f z dz d
а)
т. е. правая часть представляет собой полный
дифференциал. В связи с этим можно утверждать,
что это уравнение имеет решение всегда, т. е.
жидкость может находиться в равновесии, если и
левая часть уравнения представляет собой полный
дифференциал некоторой функции Ф, зависящей от
х, у, z. Так как
d
dx
dy
dz
x
y
z
b)
67.
Сравнив а) и b) получим условия, при которыхжидкость может находиться в равновесии
fx
; fy
; fz
.
x
y
z
A Fdl f x i f y j f z k idx jdy kdz
l
2
f dx f dy f dz d
x
l
y
z
2
1
l
Поверхность, на которой Ф = const или dФ=0,
называется эквипотенциальной или поверхностью
уровня. На этой поверхности dp =0 или р =const или
f x dx f y dy f z dz 0
68.
Равновесие жидкости в гравитационномполе
z
z0
z
p0
h
g
В этом случае имеем: fz = –
g; fx = fy = 0.
m
x
Граничные условия: z = z0;
p = p0 .
Уравнение поверхности уровня – gdz = 0 или
после интегрирования z = const
p
p
const
gz C z
g
p0
C
gz0
p p0 g z0 z p0 gh
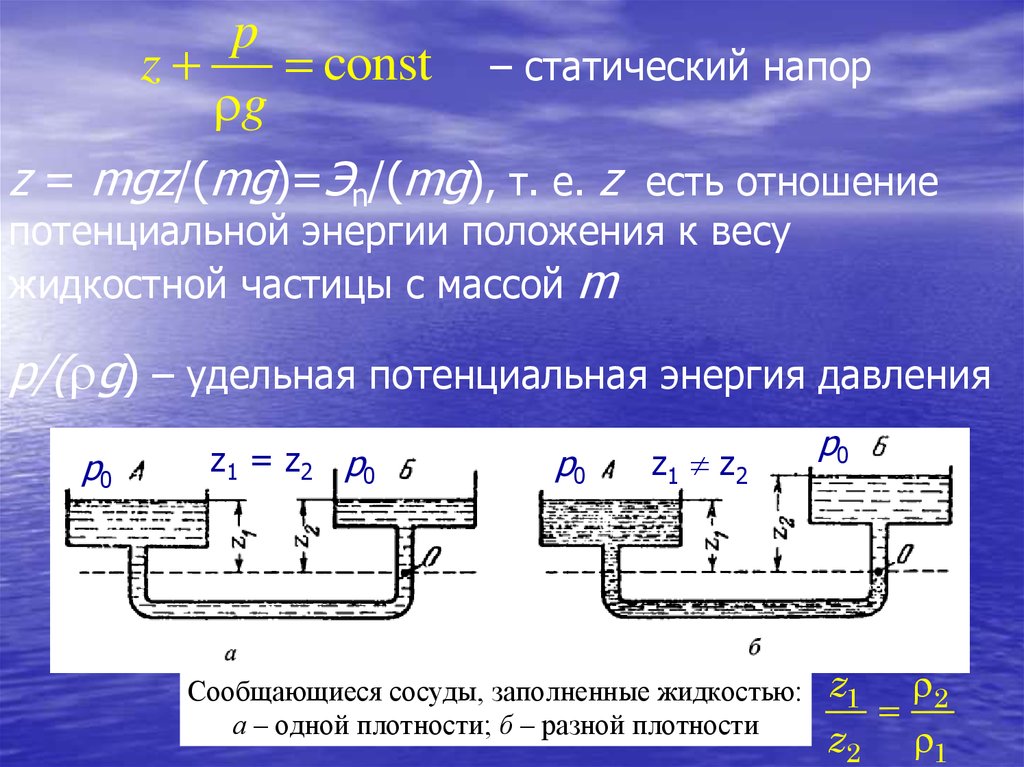
69.
pz
const
g
– статический напор
z = mgz/(mg)=Эn/(mg), т. е. z есть отношение
потенциальной энергии положения к весу
жидкостной частицы с массой m
p/( g) – удельная потенциальная энергия давления
p0
z1 = z2 p0
p0
z1 z2
Сообщающиеся сосуды, заполненные жидкостью:
а – одной плотности; б – разной плотности
p0
z1 2
z2 1
70.
F2P2 P1
F1
Схема гидравлического пресса
При изменении атмосферного
давления изменяется высота
жидкости в трубке. Это позволяет
использовать такую трубку
в качестве прибора для
измерения давления –
ртутного барометра
Для воды:
H
101325
10, 34 м
1000 9,8
71.
ЗадачаВакуумметр на барометрическом конденсаторе
показывает вакуум, равный 600 мм рт.ст.
Атмосферное давление 748 мм рт.ст.
Определить:
а) абсолютное давление в конденсаторе в Па и
в кгс/см2;
б) на какую высоту Н поднимается вода в
барометрической трубе?
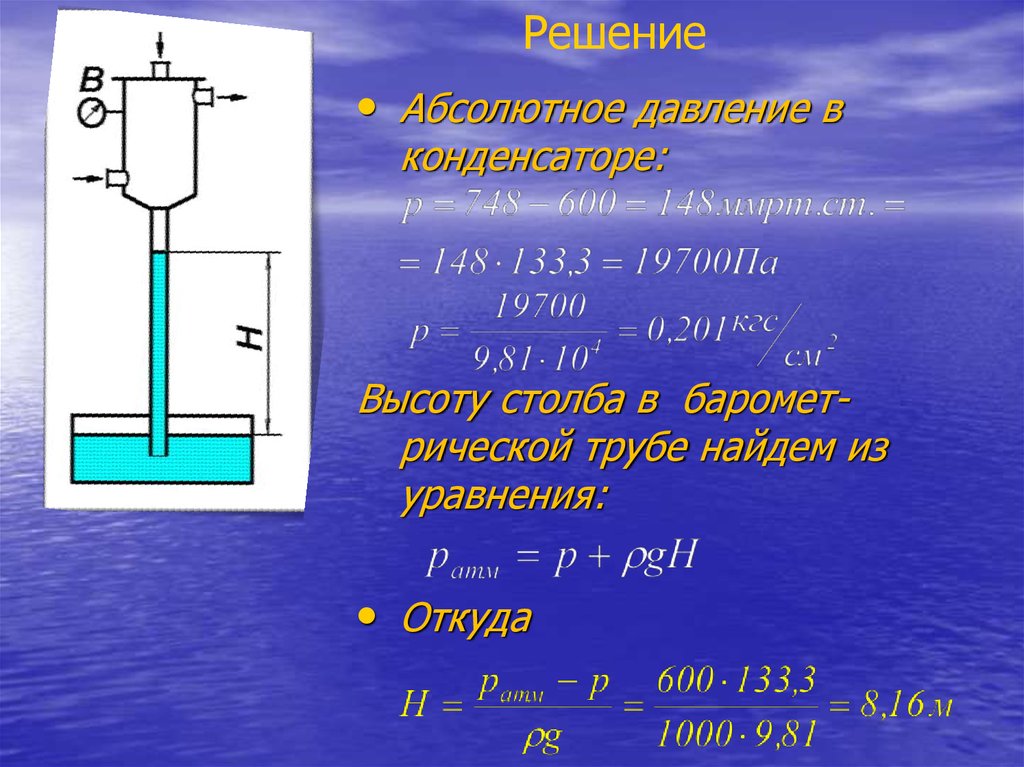
72.
Решение• Абсолютное давление в
конденсаторе:
Высоту столба в барометрической трубе найдем из
уравнения:
• Откуда
73.
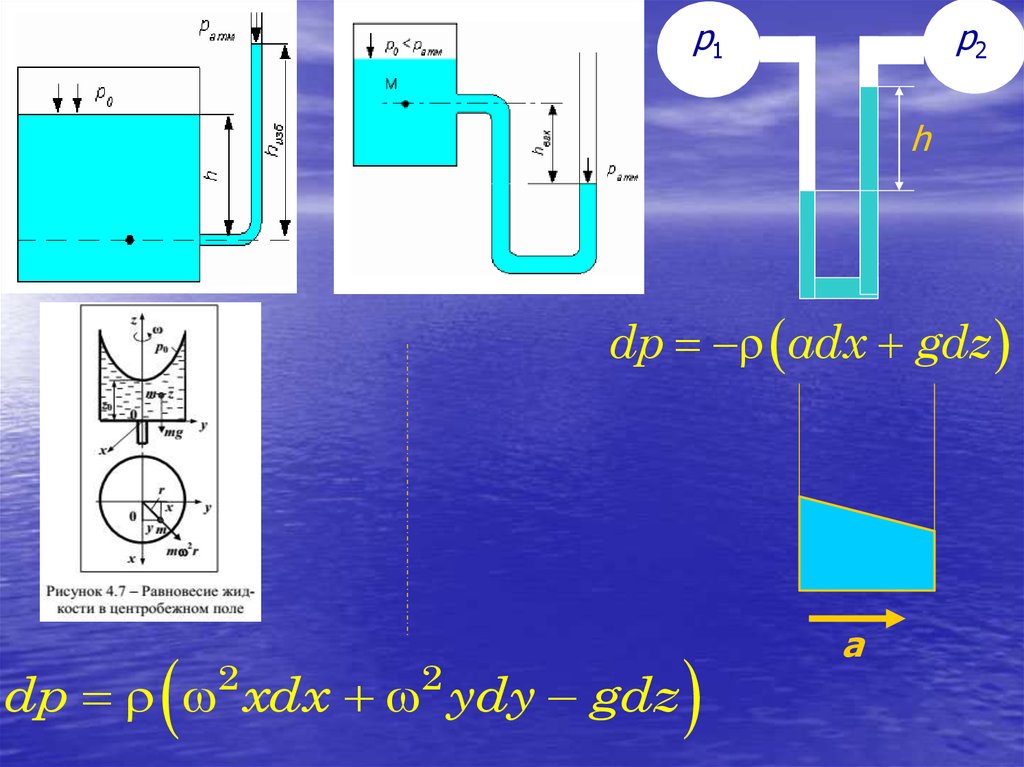
p1p2
h
dp adx gdz
dp 2 xdx 2 ydy gdz
a
74.
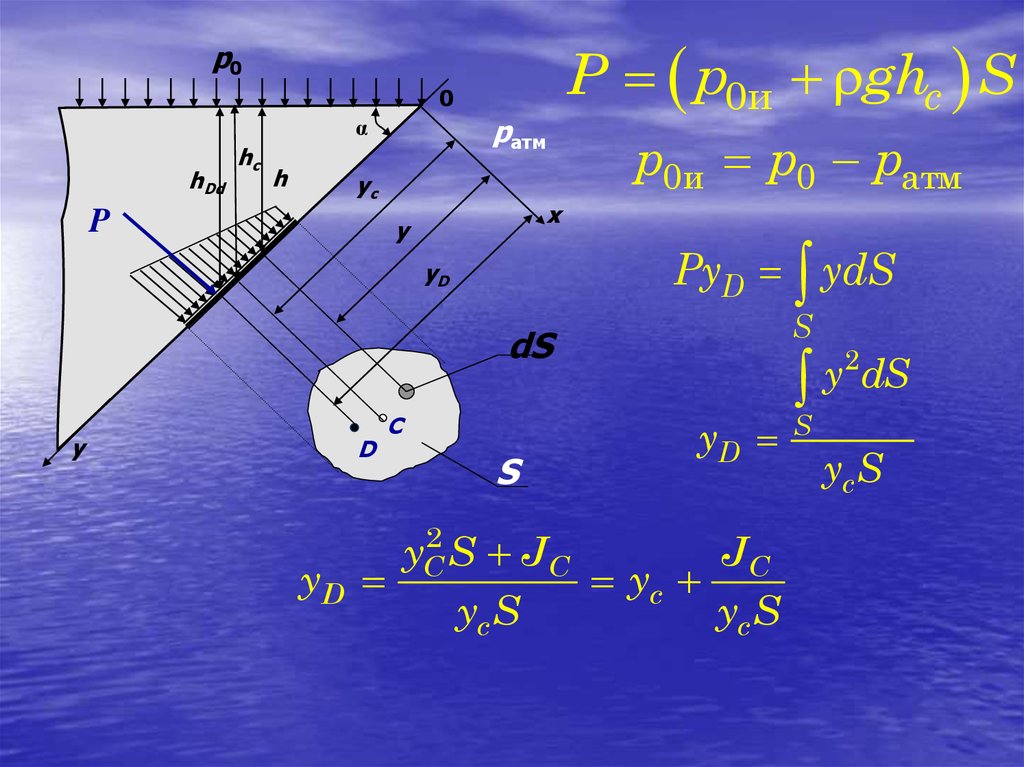
P р0и ghc Sp0
0
pатм
α
hDd
hc
h
yc
P
р0и р0 ратм
x
y
PyD ydS
yD
S
dS
y
D
C
S
yD
yC2 S JC
JC
yD
yc
yc S
yc S
2
y
dS
S
yc S
75.
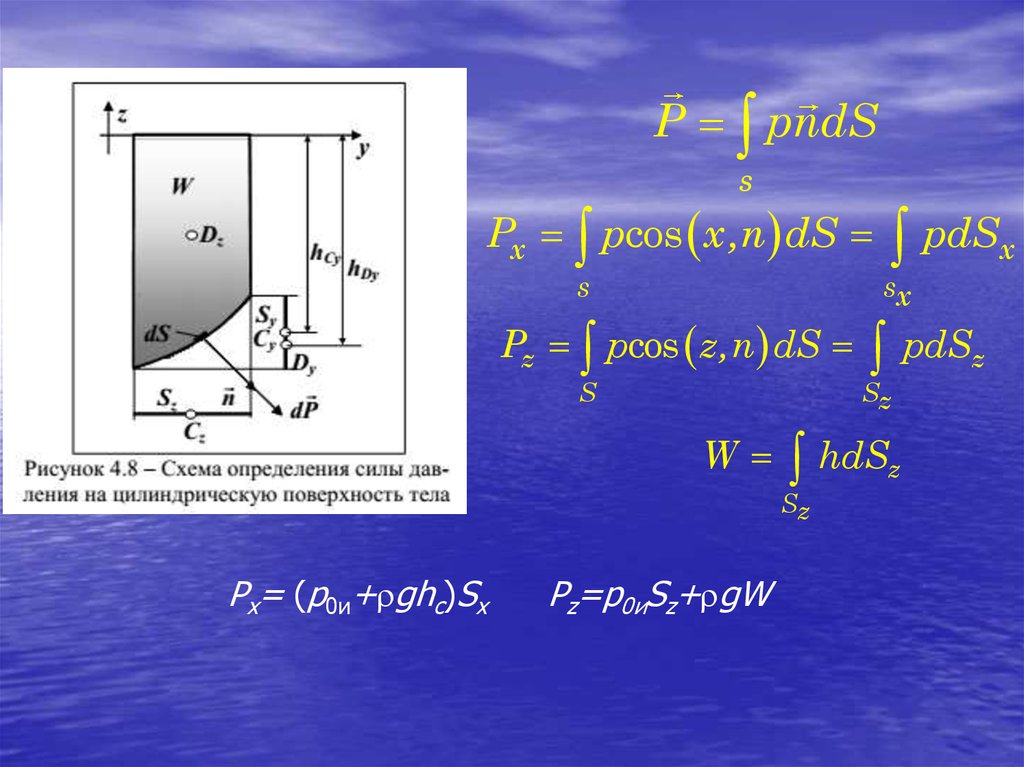
P pndSs
Px pcos x,n dS
s
Pz pcos z,n dS
S
W
Pz=p0иSz+ gW
sx
pdSz
Sz
hdSz
Sz
Px= (p0и+ ghc)Sx
pdSx
76.
77.
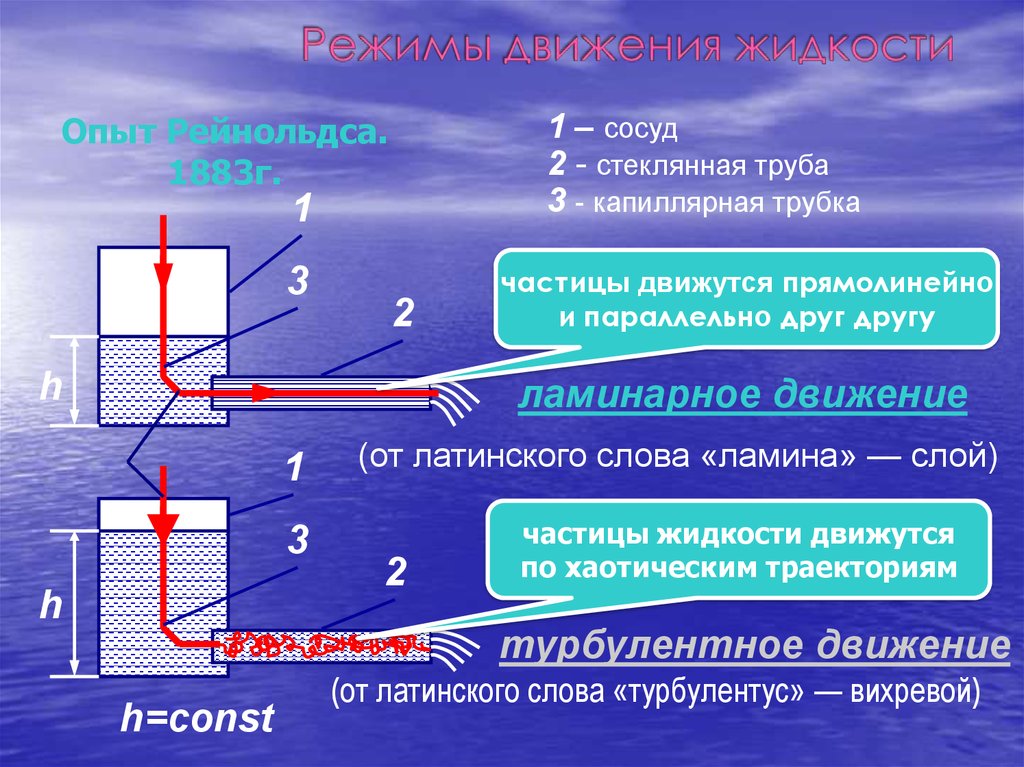
1 – сосуд2 - стеклянная труба
3 - капиллярная трубка
Опыт Рейнольдса.
1883г.
1
3
2
h
частицы движутся прямолинейно
и параллельно друг другу
ламинарное движение
1
3
h
(от латинского слова «ламина» — слой)
2
частицы жидкости движутся
по хаотическим траекториям
турбулентное движение
h=const
(от латинского слова «турбулентус» — вихревой)
78.
Опыт показывает, что переход от ламинарноготечения к турбулентному зависит от массовой
скорости жидкости ρ , диаметра трубы d
и вязкости жидкости μ.
Критерий Рейнольдса:
Reкр=2300
vd vd
Re
Re < 2300 – устойчивый ламинарный режим
2300 < Re < 10000 – неустойчиво турбулентный режим
Re > 10000 – устойчиво турбулентный режим
79.
Уравнение турбулентного течения несжимаемой жидкости (уравнение Рейнольдса)ux ux u'x
x x 'x
u y u y u'y
xy xy 'xy
uz uz u'z
xz xz 'xz
a a a ; b b b ; a b a b ; a a ; a 0; ab 0;
a a
x x
u u u u
2
ux
dux ux
dt
t
x
x y
y
x z
z
dux
' '
' '
X
x ux ux
xy ux uy
xz u'x u'z
dt
x
y
z
80.
' 'ux ux
' '
ux uy
' '
ux uz
' '
T uyux
' '
uyuy
' '
uyuz
' '
uz ux
' '
uz uy
' '
uz uz
81.
umaxv
umax
r
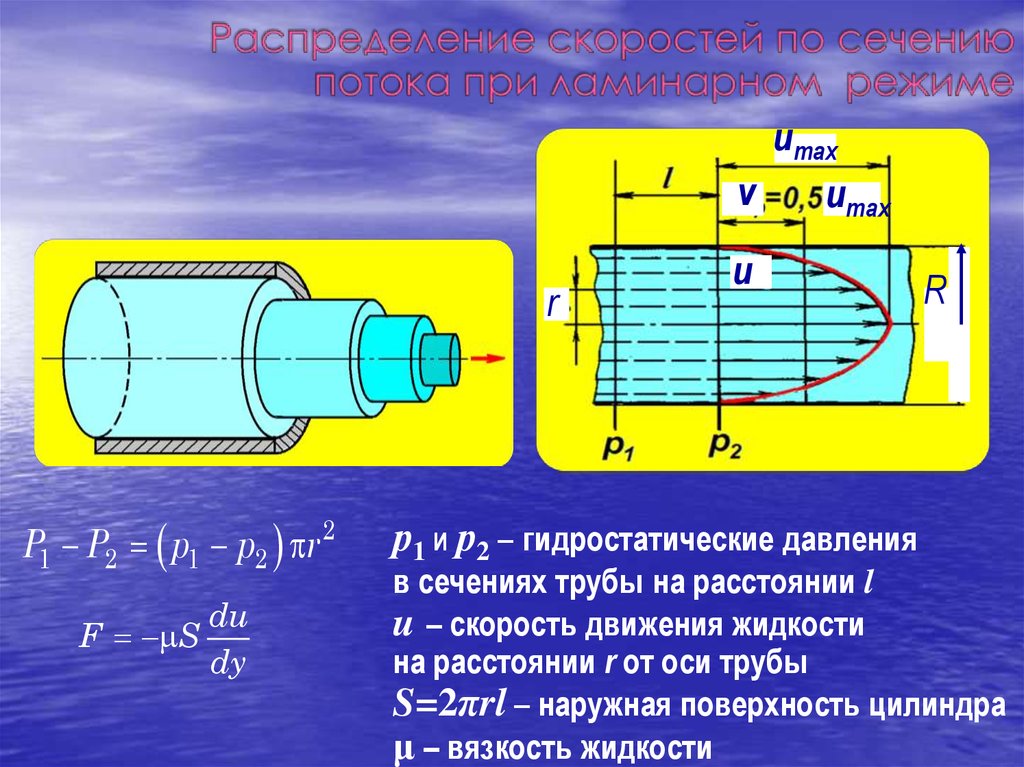
P1 P2 p1 p2 r 2
F S
du
dy
u
р1 и р2 – гидростатические давления
R
в сечениях трубы на расстоянии l
u – скорость движения жидкости
на расстоянии r от оси трубы
S=2πrl – наружная поверхность цилиндра
μ – вязкость жидкости
82.
Распределение скоростей по сечениюпотока при ламинарном режиме
Сумма проекций всех сил на ось потока равна нулю
du
p1 p2 r 2 rl
dr
2
После сокращения и разделения переменных
p1 p2
rdr du
2 l
Интегрируя с учетом граничных условий, получим
p1 p2 2
u
R r2
4 l
83.
Распределение скоростей по сечениюпотока при ламинарном режиме
Скорость имеет максимальное значение на оси трубы
umax
p1 p2 2
R
4 l
r2
u umax 1 2
R
- параболическое
распределение скоростей в сечении трубопровода
при ламинарном движении
При ламинарном режиме средняя скорость жидкости
равна половине скорости на оси трубы
v 0, 5umax
84.
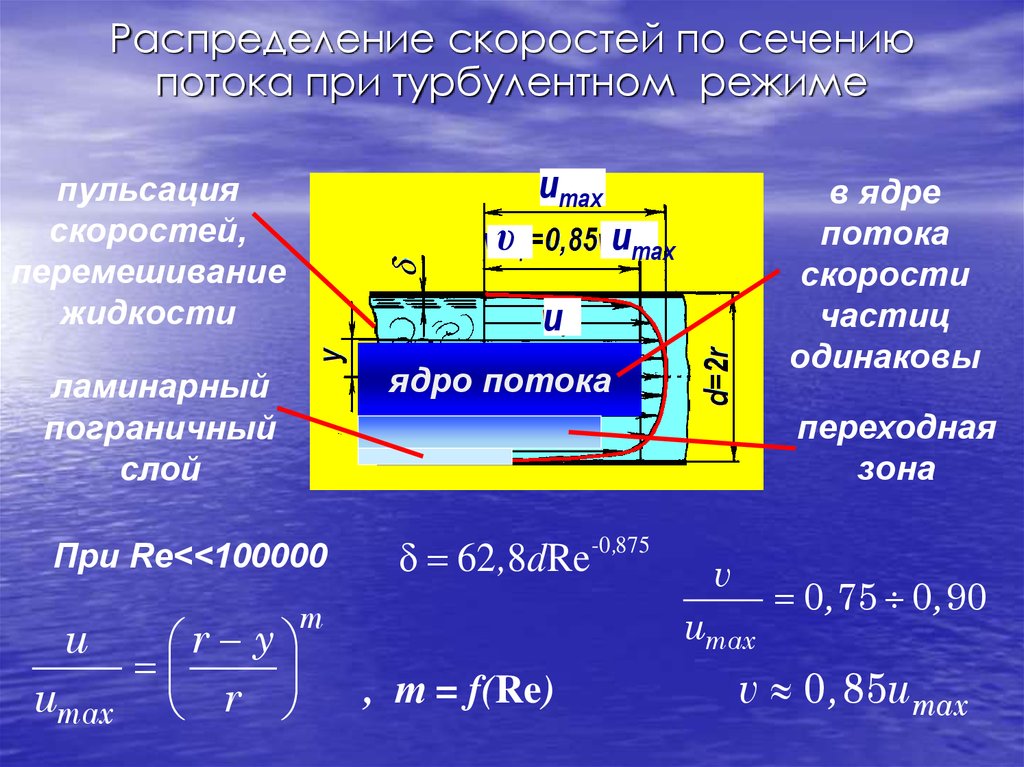
Распределение скоростей по сечениюпотока при турбулентном режиме
umax
пульсация
скоростей,
перемешивание
жидкости
vυ
umax
u
ламинарный
пограничный
слой
ядро потока
При Re<<100000
62 ,8dRe -0 ,875
u
umax
в ядре
потока
скорости
частиц
одинаковы
переходная
зона
m
r y
r
v
umax
, т = f(Re)
0 , 75 0 , 90
v 0 , 85umax
85.
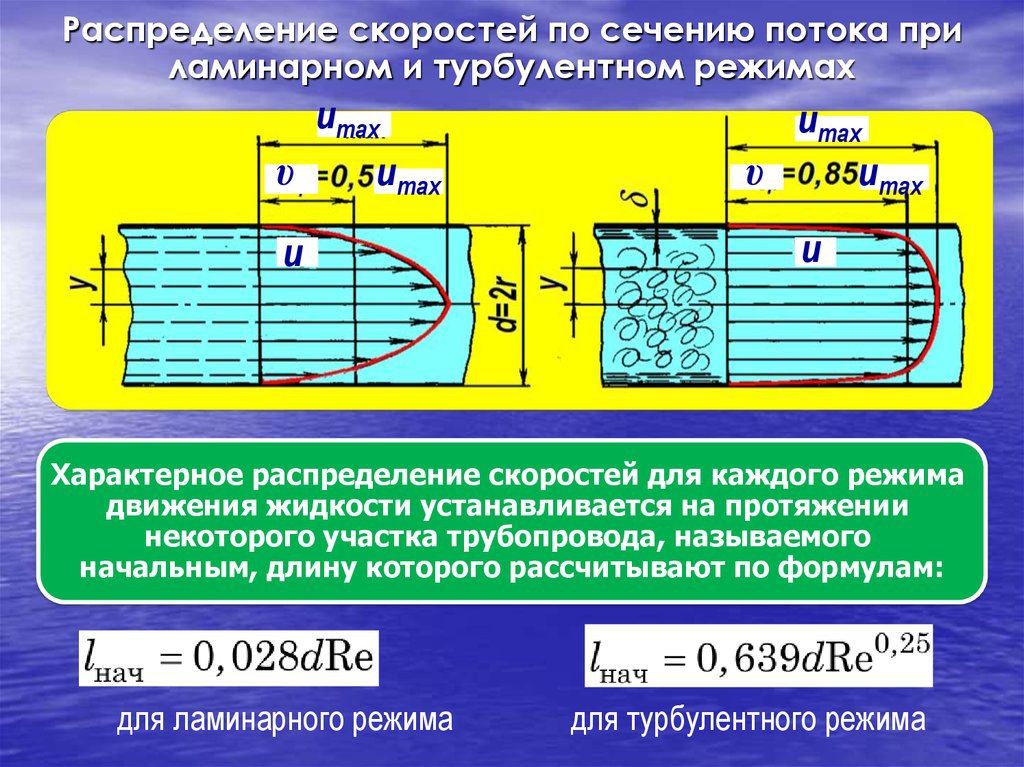
Распределение скоростей по сечению потока приламинарном и турбулентном режимах
umax
υ
umax
u
umax
υ
umax
u
Характерное распределение скоростей для каждого режима
движения жидкости устанавливается на протяжении
некоторого участка трубопровода, называемого
начальным, длину которого рассчитывают по формулам:
для ламинарного режима
для турбулентного режима
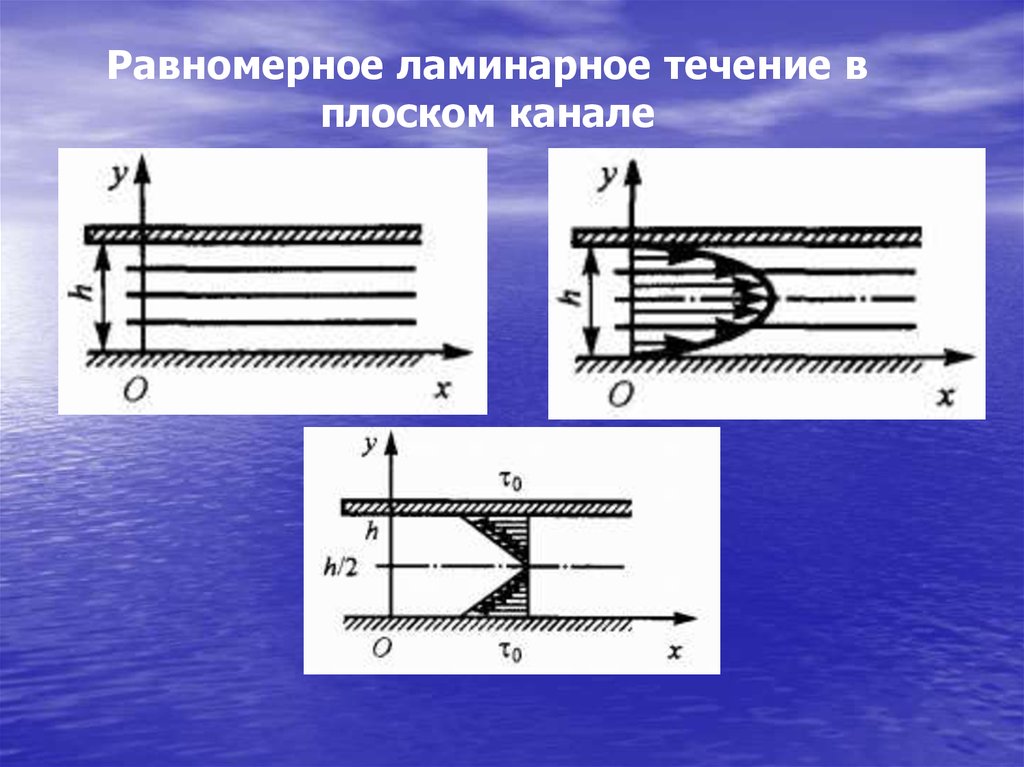
86.
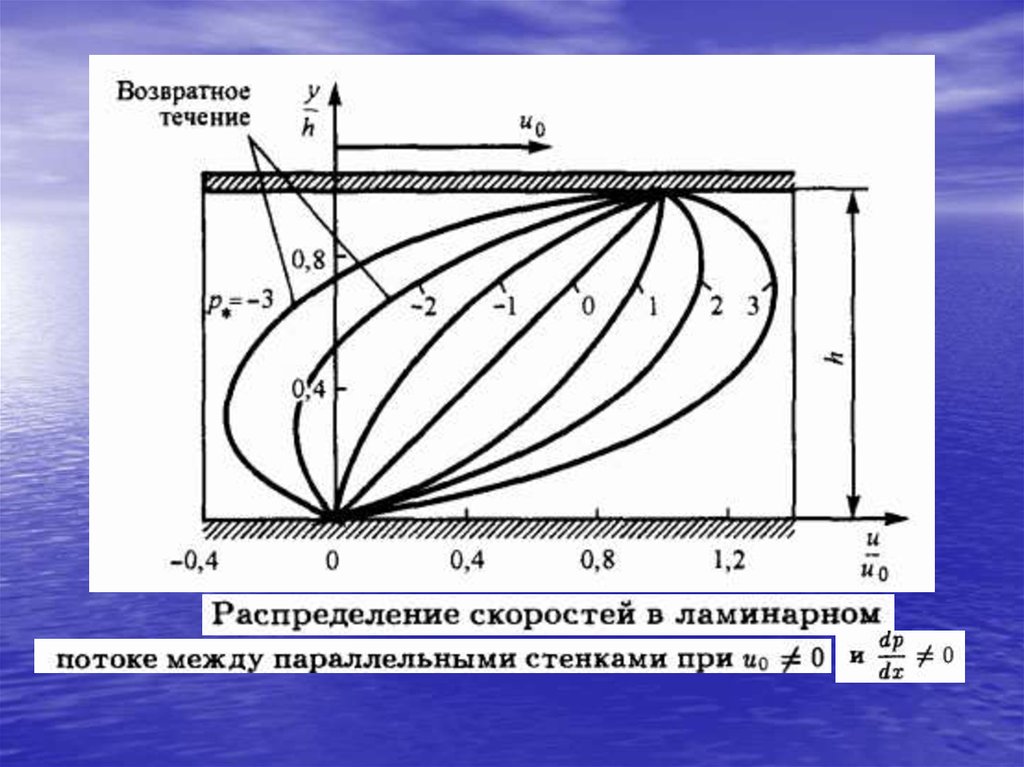
Равномерное ламинарное течение вплоском канале
87.
88.
v2
um 3
89.
90.
91.
ГИДРОДИНАМИЧЕСКИЙ ПРОЦЕССматематическая модель
решение системы сложных
дифференциальных
уравнений известными
математическими
методами
общий случай,
но не всегда возможен
экспериментальная модель
получение эмпирических
уравнений
частный случай,
применим не для всех
аналогичных явлений
ТЕОРИЯ
ПОДОБИЯ
92.
Элементы теории подобияДва процесса подобны, если описываются
тождественными уравнениями с тождественными
граничными условиями и протекают в
геометрически подобной обстановке.
Зная условия подобия, можно исследовать модельный
аппарат, машину, а потом перенести результаты испытаний
на реальный проектируемый объект. Для выявления условий
гидромеханического подобия уравнение Навье—Стокса
преобразуется к безразмерному виду.
93.
L масштаб длины; x x L ;y y L; z z L
U масштаб скорости; ux ux U ; u y u y U ; uz uz U
T масштаб времени; t t U
g масштаб массовых сил; X X g ; Y Y g ; Z Z g
p0 масштаба давлений; p p p0
uy
ux
ux
uz
1
p 1 2
Sh
ux
uy
uz
X Eu
ux
t
x
y
z
Fr
x Re
p0
L
U2
UL
Sh
; Fr
; Eu
; Re
2
UT
gL
U
Fp
Fи.л
Fи.к
Fи.к
Sh
; Fr
; Eu
; Re
Fи.к
Fm
Fи.к
Fтр
94.
Полную модель для объекта не всегда удается получить.Воспользовавшись индексами: о – объект; м – модель,
рассмотрим пример:
Пусть L0/Lм =102. Тогда из равенства чисел Фруда
U02/(gL0) = Uм2/(gLм) следует, что U0/Uм= (L0/Lм)0,5=10; а
из равенства чисел Рейнольдса
U0 L0 U м Lм
0 U0 L0
;
103
0
м
м U м Lм
Т. е. испытания модели надо проводить в среде, вязкость
которой значительно ниже вязкости среды объекта, что не
всегда удается реализовать
95.
Турбулентное течениеСхема механизма возникновения
турбулентной вязкости
96.
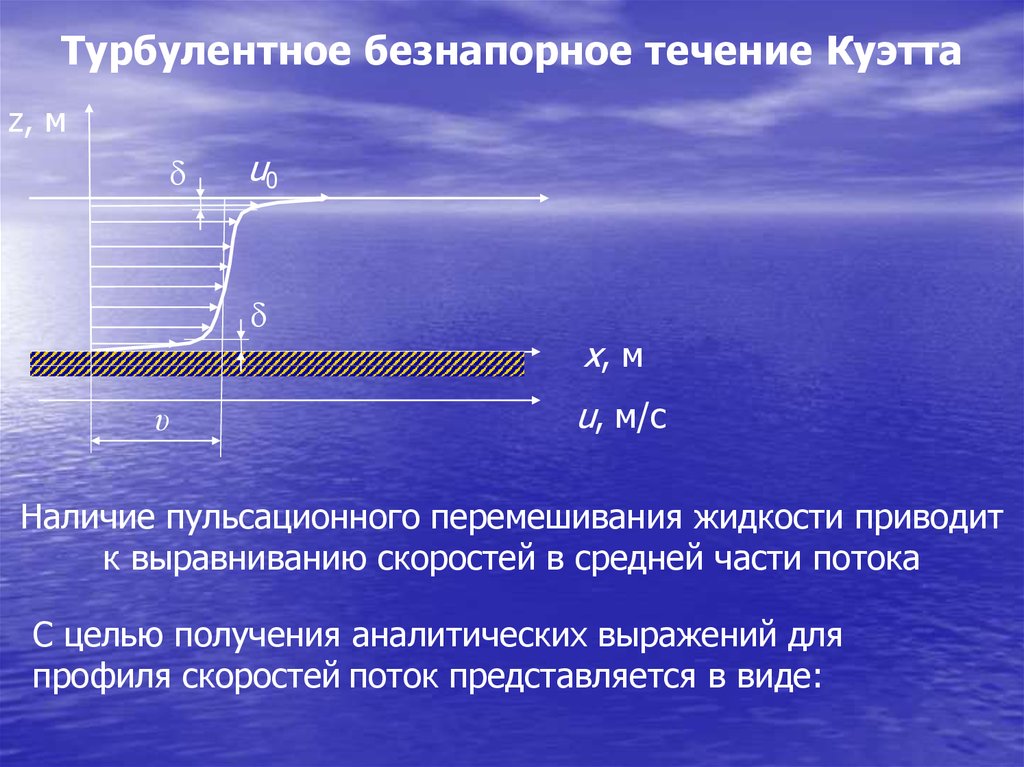
Турбулентное безнапорное течение Куэттаz, м
u0
υ
x, м
u, м/c
Наличие пульсационного перемешивания жидкости приводит
к выравниванию скоростей в средней части потока
С целью получения аналитических выражений для
профиля скоростей поток представляется в виде:
97.
ламинарного пристенного слоя толщиной , в которомпредполагается отсутствие турбулентности, и
турбулентного ядра, в котором вязкость жидкости =0. Если
> , то каналы называются гидравлически гладкими, если
< , то каналы – гидравлически шероховатые, где –
высота микронеровностей на поверхности канала.
Естественная
шероховатость
kэ
k
98.
При установившемся течении Куэтта:dux
x ux ux 0; x xy ux u y 0.
0; fx = 0;
x
dt
ux
ux
ux uz 0
ux uz C1 л т 0
z z
z
Профиль скоростей в ламинарном слое.
Поскольку в нем отсутствует турбулентность, т. е. ux uz 0,
то
ux
0
z
Граничные условия: при z = 0
Интегрируя, получим
ux 0
0 z
ux u z
ux
u
99.
Профиль скоростей в турбулентном ядре потока.Приняв = 0, т. е. предположив, что вязкостные напряжения
в потоке малы по сравнению с турбулентными л = 0, получим
ux uz 0 т
первое допущение о постоянстве
для решения данной задачи необходимо иметь одну
дополнительную зависимость, связывающую турбулентное
напряжение т с уже имеющимися параметрами течения.
Одной из первых моделей, устанавливающих такую связь
является модель Прандтля (1929 г.)
Если ввести понятие турбулентной вязкости т , то
dux
т т
dz
а)
100.
то исходя из аналогии с вязкостью газа можно записатьт lu ,
b)
где ℓ– длина пути перемешивания, т. е. пути, при
прохождении которого жидкостная частица теряет
индивидуальность, смешиваясь с остальным потоком; u —
среднее значение пульсационной скорости, называемой
динамической скоростью
Согласно гипотезе Прандтля
l æz,
с)
второе допущение о прямой
пропорциональности
где æ — коэффициент пропорциональности, æ < 1.
101.
u ux uz12
Поскольку в ядре потока
ux uz т 0 , то u 0
d)
Подставляя d), c), b) в а) получим
u 2
dux
æzu
dz
После интегрирования будем иметь
u
ux
lnz C
æ
e)
Постоянная С определяется из условия равенства скоростей
на границе ламинарного слоя и ядра потока. При z =
u 2
u
C
ln
æ
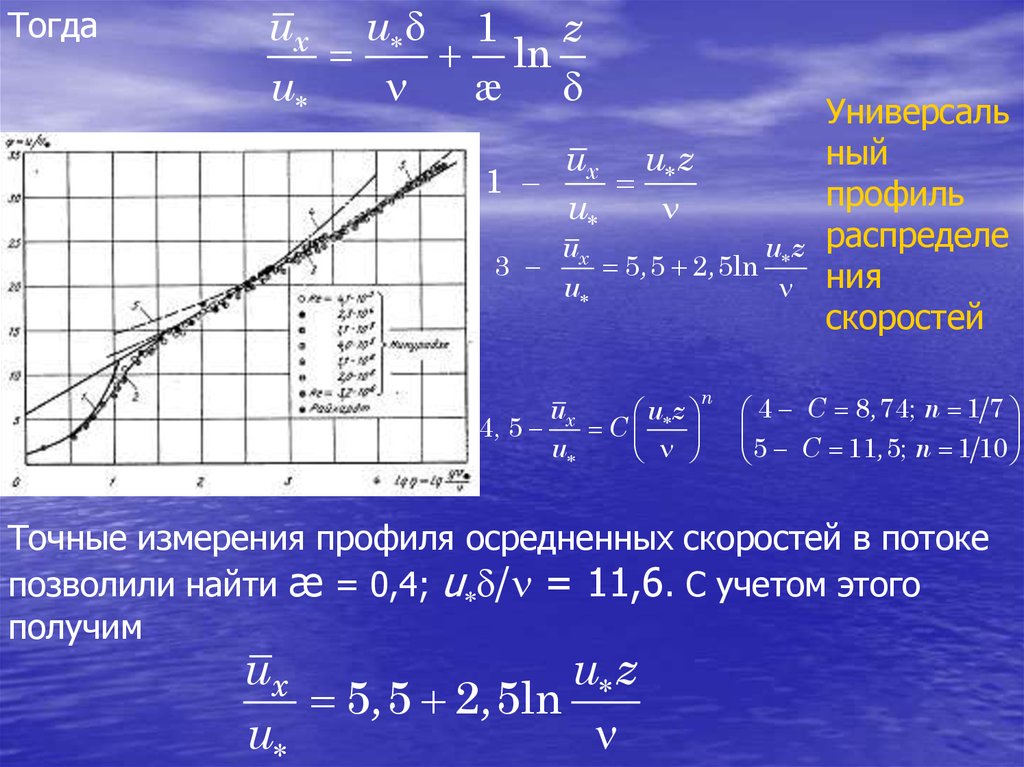
102.
Тогдаux u 1
z
ln
u
æ
Универсаль
ный
ux u z
1
профиль
u
ux
u z распределе
3
5, 5 2, 5ln
u
ния
скоростей
u
u z
4, 5 x C
u
n
4 C 8, 74; n 1 7
5 C 11, 5; n 1 10
Точные измерения профиля осредненных скоростей в потоке
позволили найти æ = 0,4; u / = 11,6. С учетом этого
получим
ux
u z
5, 5 2, 5ln
u
103.
Следует отметить, что ни одно из рассмотренных допущенийне согласуется с реальностью. Так, например, рассматривая
графическую интерпретацию ламинарного течения в трубе
будем иметь
104.
Равномерное движение цилиндрического элемента жидкостирадиусом r и длиной L возможно, если
2L
p
r
а равномерное движение всей жидкости в трубе длиной L и
радиусом R при
2L
p
0
R
Поскольку р = const, то
r
0
R
r R z
f)
z
0 1
R
Кроме этого из уравнения f) с учетом ф – лы Дарси-Вейсбаха
следует
v
0
8
2
u v
8
g)
105.
В соответствии с результатами экспериментов, длина путиперемешивания ℓ достигает максимума на оси трубы.
l/r
1
4
2
1 – гипотеза Прандтля; 2 –
гипотеза Кармана; 3 – кривая
Альтшуля; 4 – кривая Конакова; 5 –
кривая Саткевича
0,2
0,1
0
3
0,2
0,4
0,6
0,8
5
z/r
Сопротивление гидравлически гладких и
шероховатых труб при турбулентном режиме
течения жидкости
Для расчета падения давления по длине горизонтальной
трубы применяется уравнение Дарси—Вейсбаха, в котором
неизвестными величинами являются средняя скорость υ и
коэффициент гидравлического трения .
106.
Алгоритм определения этих величинВоспользовавшись универсальным профилем скоростей
находят среднюю скорость
u r0
v
1, 75 2, 5ln
,
u
а далее из уравнения g) после преобразований
1
2lg Re 0, 8 =
0,3164
0,25
Re
формула Блазиуса
Гидравлически гладкие трубы характеризуются неравенством
u u
11, 6. , что соответствует условию
или
d
Re 20
107.
Гидравлически шероховатые трубы характеризуютсянеравенством > или
представить в виде
u
11, 6
d
Re 500
, которое можно
В этом случае постоянную интегрирования С в уравнении e)
находят из условия:
2
при z =
u
ux
11, 6u , что дает
ux
z
C1 2, 5ln
u
Определив среднюю скорость потока v , получим
r0
v
C2 2, 5ln
u
А далее с учетом уравнения g) будем иметь
108.
r08
С3 2, 5ln
Это уравнение хорошо аппроксимируется более простым
0,11
d
0 ,25
68
0,11
d
Re
формула Шифринсона
0 ,25
формула Альтшуля
109.
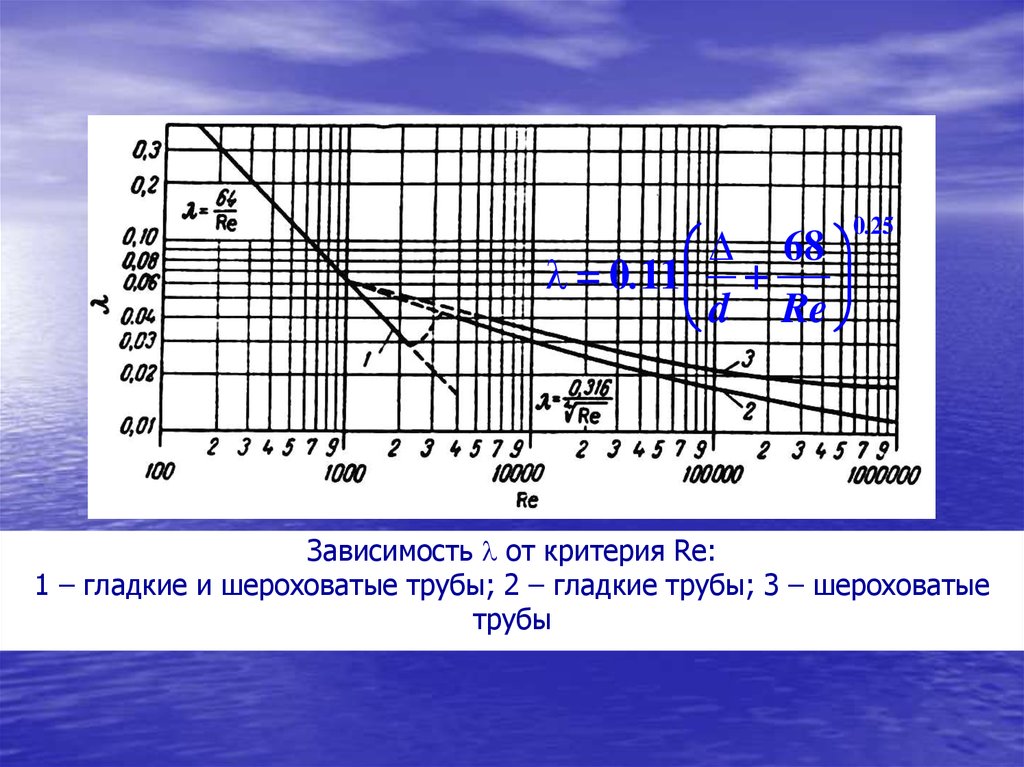
680.11
d
Re
0.25
Зависимость от критерия Re:
1 – гладкие и шероховатые трубы; 2 – гладкие трубы; 3 – шероховатые
трубы
110.
Уравнения пограничного слоя111.
Тонкий пристенный слой переменной толщины ,формирующийся при обтекании плоской пластины с
заостренной передней кромкой набегающим равномерным
потоком вязкой жидкости, называют пограничным слоем. В
этом слое жидкость заторможена за счет вязкостных сил
трения, а скорость изменяется от нуля на стенке до значения,
близкого к скорости набегающего потока U.
2ux
y
2
2ux
x 2
На внешней границе очевидно, что ux = U
p U2
С,
g 2 g
1 dp
dU
т.е.
U
dx
dx
u x
u x
2u x
dU
ux
uy
U
2
x
y
dx
y
112.
Интегральное соотношение пограничного слояd
dU 0
2
U 2 U 1
dx
dx
ux ux
2 1
U
U
0
ux
1 1
U
0
dy
dy
толщина потери импульса
толщина вытеснения, определяющая
насколько смещаются линии тока
основного потока из-за уменьшения
скоростей в пограничном слое или
иначе это толщина слоя, в каждом
сечении которого расход невозмущенного потока 1U равен расходу,
вытесненному из пограничного слоя к
соответствующему сечению
113.
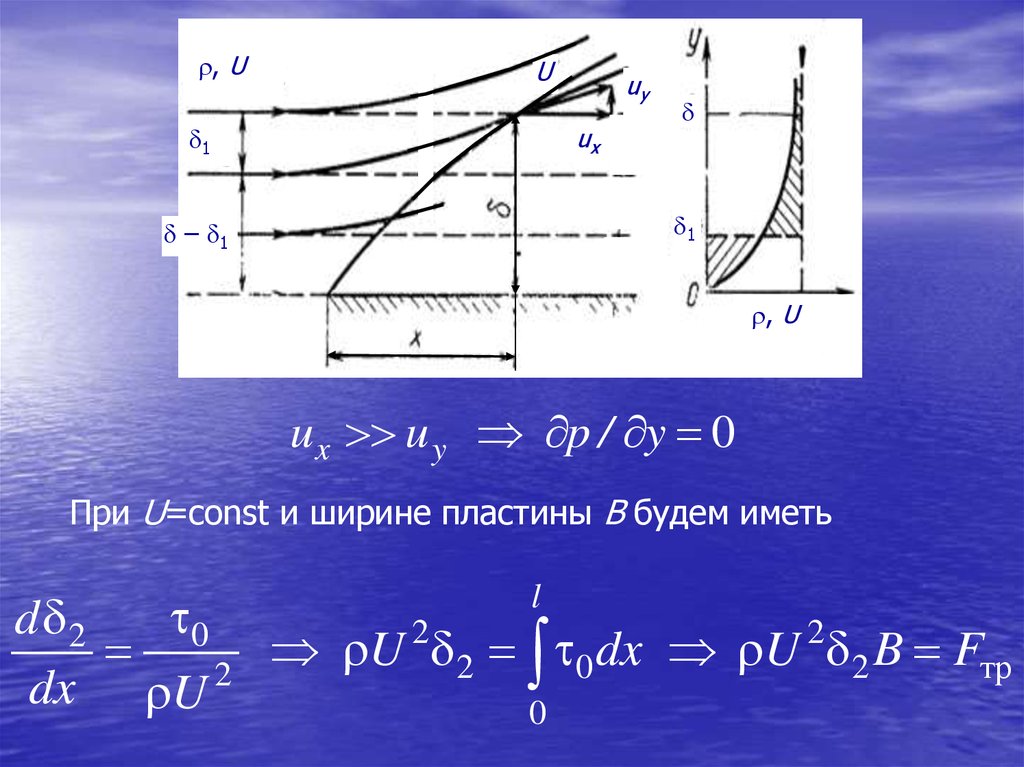
, UU
uy
ux
1
1
– 1
, U
ux u y p / y 0
При U=const и ширине пластины В будем иметь
0
d 2
2
2
U
dx
U
B
F
2
0
2
тр
2
dx U
0
l
114.
ОДНОМЕРНЫЕ ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИодномерными называют потоки, в которых
гидродинамические величины (скорость, давление) зависят
только от одной геометрической координаты. Если реальные
потоки жидкости в каналах различной формы
характеризовать средней расходной скоростью и давлением
на оси потока, то такой поток можно считать одномерным
Уравнение Бернулли для потока вязкой жидкости
p1
υ12 0 υ
p2
υ22
z1
1
dl z2
2
hW
g
2 g g l t
g
2g
1
dT
1
hw
c p
dV
DdV
gQ V
dt
gQ V
115.
υl υ
4S
hw hмс hl ; hмс ; hl
; dэ
.
2g
dэ 2 g
2
2
Уравнение Бернулли для сети с насосом
Если выполняется условие
2
1υ1
2
2υ2
p1
p2
z1
z2
g 2 g
g
2g
то для обеспечения подачи жидкости необходимо сообщить
ей энергию внешним источником, или насосом.
Удельная энергия, сообщаемая жидкости насосом, называется
полезным напором и обозначается Н, м. Уравнение баланса
энергий в этом случае имеет вид
2
1υ1
2
2υ2
p1
p2
H z1
z2
hw
g 2 g
g
2g
116.
Это уравнение позволяет для заданной схемы трубопроводоврассчитывать Н, а следовательно, подобрать насос. Поскольку
слагаемые
2
то
2
υ1
υ2
2
1
hw f Q ,
2g
2g
p2 p1
H z2 z1
f Q H ст аQ2
g
Уравнение
характеристики
сети
117.
Виды местных сопротивленийВнезапное расширение. Теорема Борда - Карно
Расчетная схема к определению потерь
при внезапном расширении
Из уравнения Бернулли следует
p1 p2
hв р
g
2
υ1
2
υ2
2g
118.
Выигрыш в давлении определим, воспользовавшись теоремойоб изменении количества движения жидкости
dK x
=R px
dt
Тогда
dK x
Q υ2 υ1 ;
p1 p2 υ22 υ1υ2
dt
g
g
R px p1 p2 S 2 .
2
2
υ
υ
υ1
υ2
2
1
hв р
1
2
2g
2g
2g
2
С учетом уравнения неразрывности υ1S1 = υ2S2 , получим
S1
1 1
S2
2
S2
2 1
S1
2
119.
Постепенное расширениеПотерю напора в диффузоре можно условно рассматривать
как сумму потерь на трение и расширение. При небольших
углах возрастают потери по длине, а сопротивление на
расширение становится минимальным. При больших углах
наоборот: возрастает сопротивление на расширение.
Коэффициент сопротивления диффузора можно определить
по следующей формуле
120.
121.
122.
123.
124.
υ12gh
2
S1
2 1
S2
125.
126.
Ротаметр (рис. 7.12) – это расходомер,выполненный из стеклянной конической
трубки, внутри которой находится
поплавок. При расходе жидкости Q
поплавок устанавливается по высоте а.
Установим вид зависимости Q = f(a).
Запишем условие равновесия
вертикальных составляющих сил,
действующих на поплавок
п gVп ж gVп p1 p2 Sп 0
где Vп – объем поплавка; ρп – плотность
материала поплавка; Sп – площадь
сечения поплавка.
127.
Поскольку величины двух первых слагаемых не зависят отрасхода, то для прибора р1 – p2 = const. Следовательно,
гидравлические потери, возникающие при обтекании
поплавка,
p1 p2
υк2
hw
g
2g
Поскольку площадь кольцевого канала Sк = S – Sп,
то скорость жидкости υк = Q/(S – Sп) = const.
При выполнении условия S = S0+ka (k – коэффициент пропорциональности) окончательно получим
Q = υк(S0 – Sп + ka).
128.
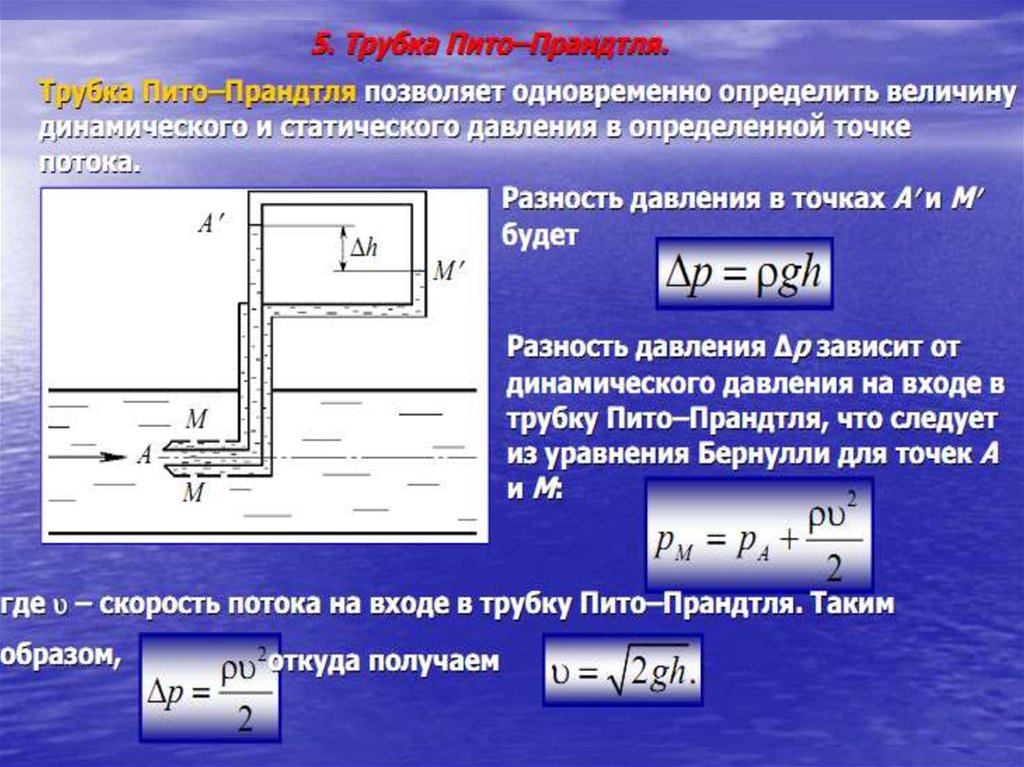
плоский зондИзмерив перепады уровней h2—h1 и h2—h3, каждый из
которых зависит от значения скорости u и угла набегания
потока, получаем возможность нахождения u и
129.
Истечение жидкостиПри истечении жидкости через отверстие или насадки из
сосуда под давлением р0 для расчета скоростей и расходов
используются зависимости
υ 2 gH ; = υ υт ;
Q S0 2 gH ; Q Qт
130.
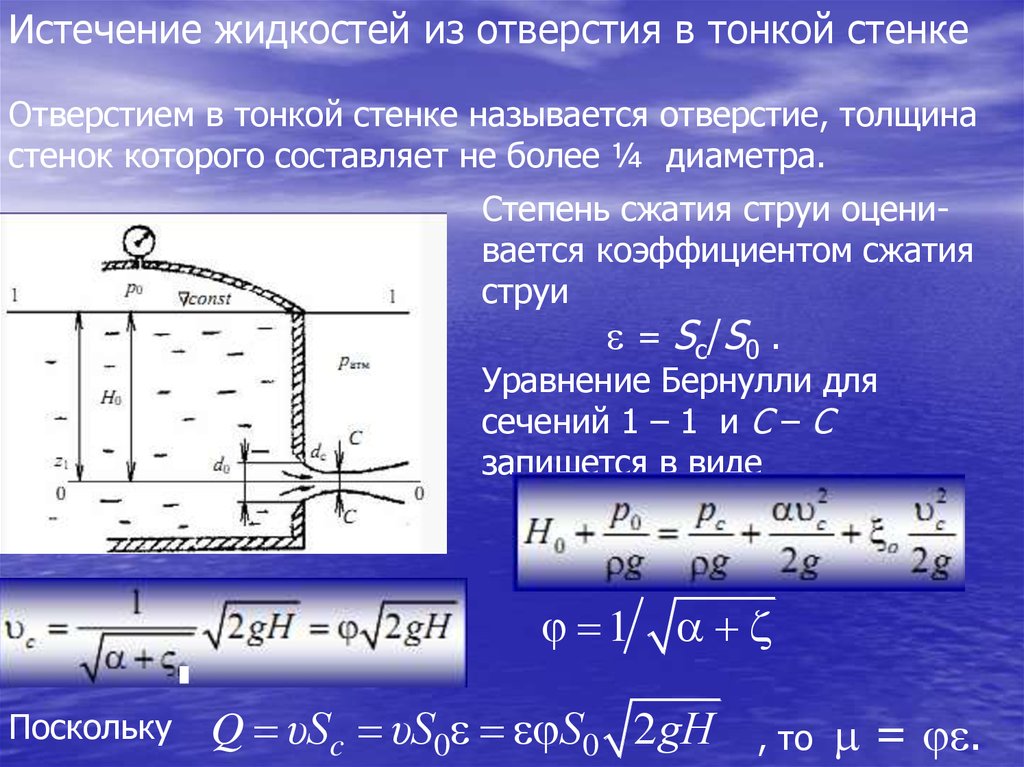
Истечение жидкостей из отверстия в тонкой стенкеОтверстием в тонкой стенке называется отверстие, толщина
стенок которого составляет не более ¼ диаметра.
Степень сжатия струи оценивается коэффициентом сжатия
струи
= Sс/S0 .
Уравнение Бернулли для
сечений 1 – 1 и С – С
запишется в виде
1
Поскольку
Q υSc υS0 S0 2 gH
, то
= .
131.
132.
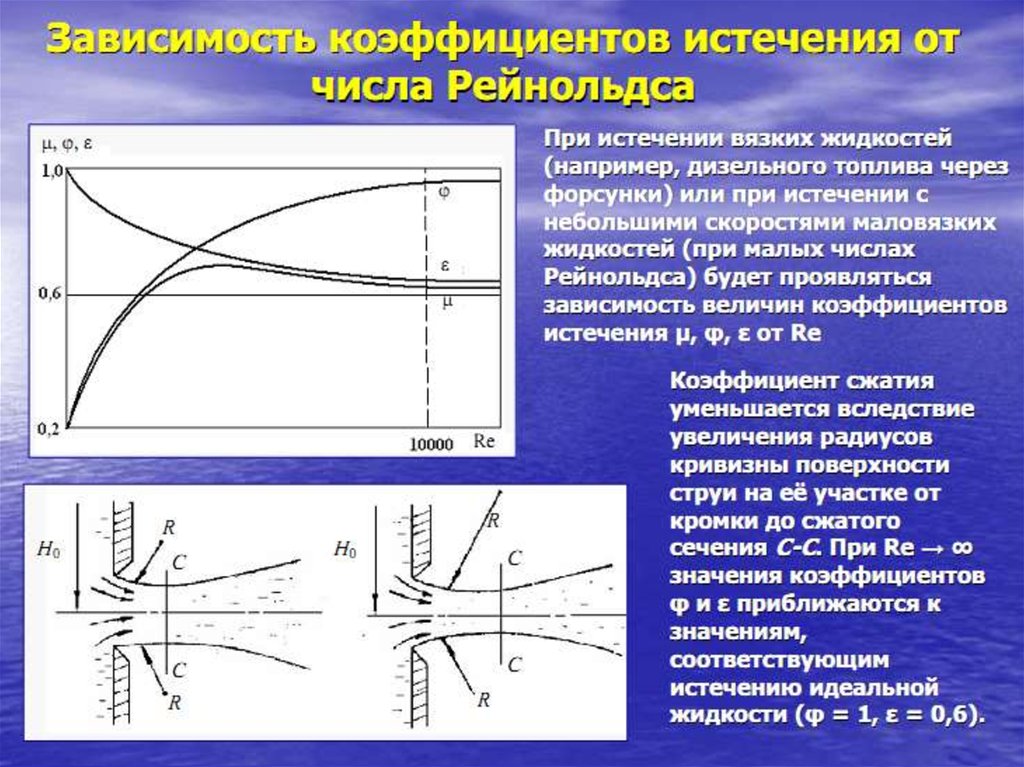
Экспериментально установлено, что при турбулентномрежиме истечения = 0,62 – 0,64; = 0,60 – 0,62; при
ламинарном и существенно зависят от Re.
Истечение жидкости через цилиндрический насадок
Насадком называется короткая труба длиной от 3 до 5 его
диаметров, присоединенная к отверстию. При расчете
насадков потерями напора по длине обычно пренебрегают.
1
1
h
2
2
133.
При входе жидкости в патрубок в сечении C – C происходитсжатие струи до величины Sс. Далее следует расширение
потока до величины S0. В уравнении Бернулли, записанном
для сечений 1 и 2, z1=h; z2=0;
hw=hc+hв.р+hl, где
2
hc cυc
/ 2g
hв р
υ1 = 0; p1 = p0; p2 = p0;
υ2 υc
2
2g
Для коротких насадков hl можно пренебречь. С учетом
υc Sc υ2 S0 , Sc / S0 ,
получим выражения для скорости и расхода. При этом
1
1 1 1 ; =
2
2
134.
Экспериментально найдено, что при турбулентном истечении=0,80 – 0,82. Длина патрубков l принимается обычно равной
3—4 диаметра. Это обеспечивает завершение расширения
потока внутри насадка. Если составить уравнение Бернулли
для сечений с и 2, то при =1 найдем
pc p2
1
0,
g
2g
2
υ2
т. е.
рс<р2.
Картина истечения между сечениями 1 и С аналогична
картине истечения через отверстие, но в насадке жидкость
истекает в область пониженного давления. Этим объясняется
увеличение расхода Q по сравнению с отверстием.
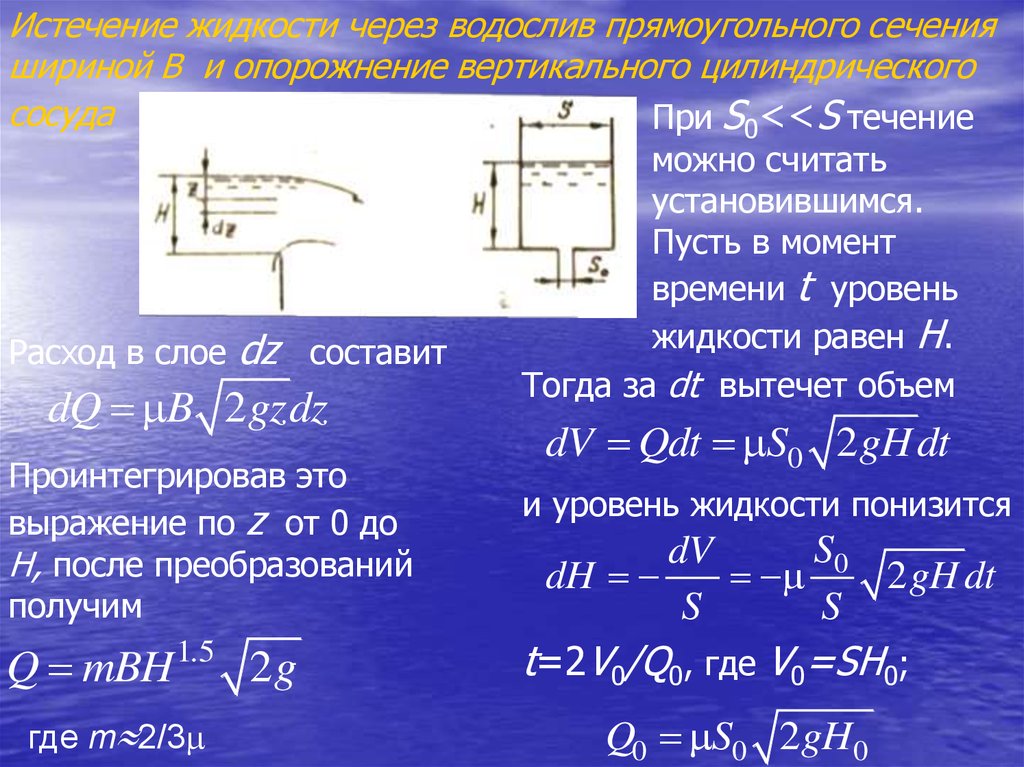
135.
Истечение жидкости через водослив прямоугольного сеченияшириной В и опорожнение вертикального цилиндрического
сосуда
При S0<<S течение
dz составит
dQ B 2 gzdz
Расход в слое
Проинтегрировав это
выражение по z от 0 до
Н, после преобразований
получим
Q mBH 1.5 2 g
где m 2/3
можно считать
установившимся.
Пусть в момент
времени t уровень
жидкости равен H.
Тогда за dt вытечет объем
dV Qdt S0 2 gH dt
и уровень жидкости понизится
S0
dV
dH
2 gH dt
S
S
t=2V0/Q0, где V0=SH0;
Q0 S0 2 gH0
136.
137.
138.
139.
140.
141.
142.
Поле скоростей и давлений в циклонном устройствеВ отличие от ранее рассмотренного относительного покоя, где
вращение внутренним слоям жидкости передавалось за счет
сил трения, в циклоне движение центральных слоев происходит за счет перемещения вращательно движущейся жидкости
от периферии к центру
При движении жидкости в плоскости ху координата z=const и
полный дифференциал уравнения
Бернулли можно записать в виде
p
d udu
а)
Поскольку радиальная составляющая скорости uR<<u, то в
уравнении движения Эйлера при проектировании его на
радиальное направление можно пренебречь слагаемым
duR/dt. Учитывая, что
p
p
2
получим
2 r
F r r gradp r
r
r
143.
2p
p
u
d 2 rdr d dr
b)
r
Из равенства а) и b), после интегрирования с начальным
условием u=u0 при r=r0 получим
ru r0u0 C
, а также
r 2
p p0
0 1
2 r
u02
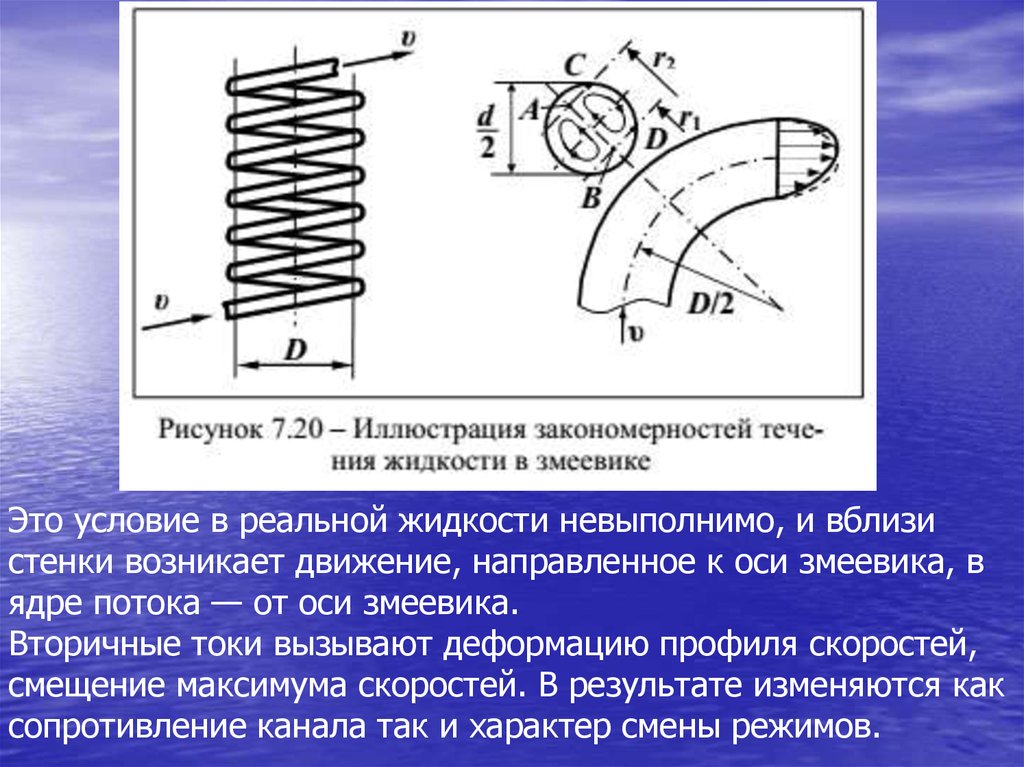
Вторичные токи в реальной жидкости
Вторичными называются течения, возникающие в поперечном
сечении каналов из-за наличия вязкости жидкости. В качестве
примера рассмотрим течение жидкости в цилиндрическом
змеевике, выполненном из трубы диаметром d. В центре потока из-за наличия плавного поворота создается центробежное
поле давлений и pA>pB . В жидкости, примыкающей к стенке,
движение отсутствует, т. е. центробежное поле давлений
возникнуть не может. Уcловие отсутствия движения жидкости
в поперечном сечении— это равенство давлений при r=const,
т. е. pA>pC; pB>pD .
144.
Это условие в реальной жидкости невыполнимо, и вблизистенки возникает движение, направленное к оси змеевика, в
ядре потока — от оси змеевика.
Вторичные токи вызывают деформацию профиля скоростей,
смещение максимума скоростей. В результате изменяются как
сопротивление канала так и характер смены режимов.
145.
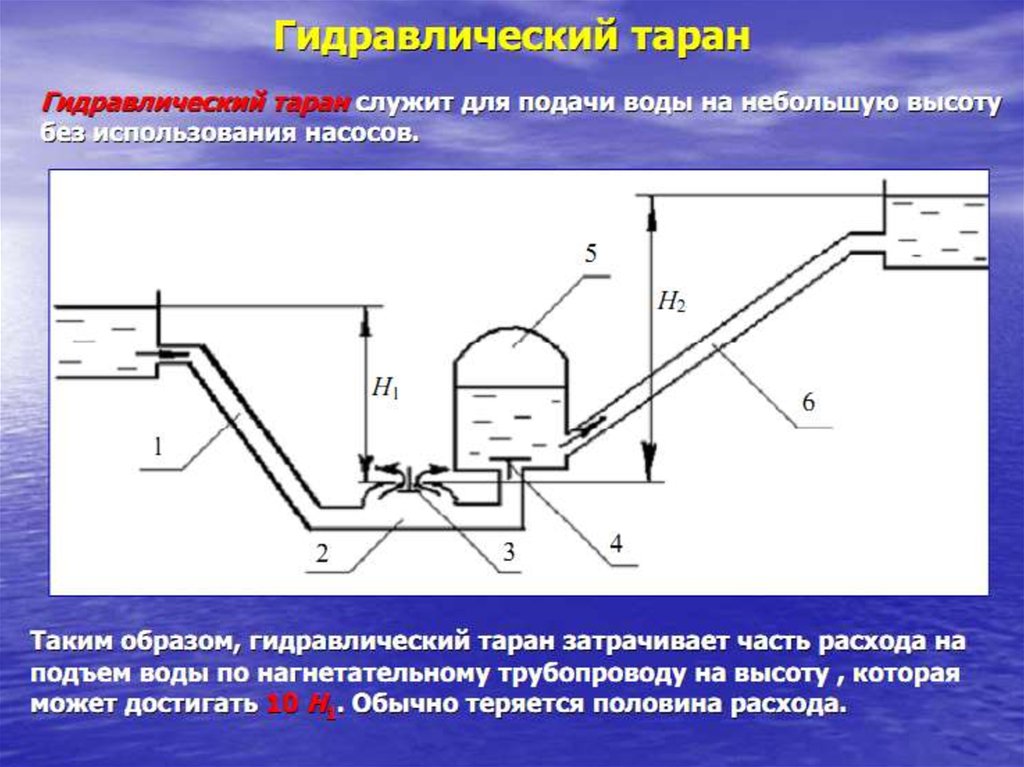
зм 1 3,54d / DГидравлический удар в трубах
Если внезапно остановить
движущийся в трубе поток
жидкости, то изменение
количества движения вызовет
возникновение избыточной
силы давления жидкости на
задвижку
146.
Очевидно, что абсолютно несжимаемая жидкость вызвала быбесконечное по величине давление при мгновенной остановке
в недеформируемом трубопроводе. Однако в результате
сжимаемости реальных жидкостей остановка жидкости в
трубе даже при мгновенном закрытии заслонки происходит во
времени, и волна давления распространяется в среде со
скоростью, равной скорости звука с. Таким образом, остановка жидкости на участке длиной х произойдет за время t=x/c.
При этом будем иметь K S l x v0
dK K 0 K Sxυ0
Sυ0c
dt
t
xc
В результате изменения количества движения возникнет
R p0 p S pS p cυ0
Для воды р = 103 1,435 103 1= 1,435 106 = 14,4 ати



















































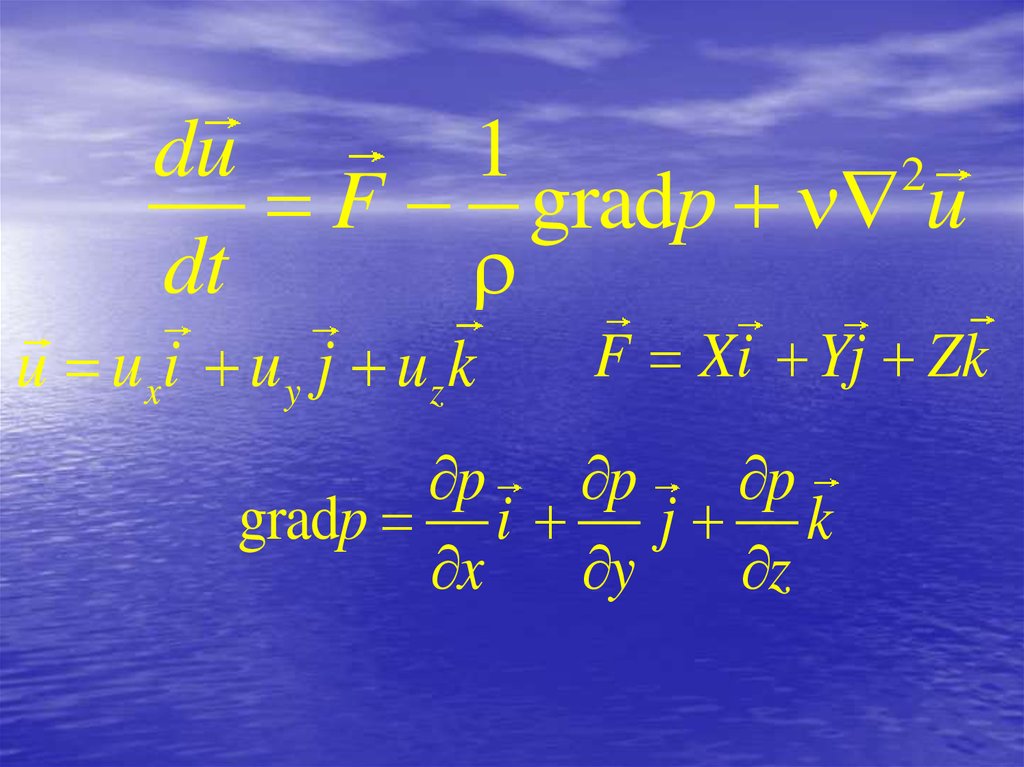


































































 Физика
Физика








