Тема №5. Фрактальная графика

1. Компьютерная графика

Москин Николай Дмитриевич
Институт математики и информационных
технологий
Петрозаводский государственный университет
1

2. § 5 Фрактальная графика

Фрактал (лат. fractus – дробленый, состоящий
из фрагментов) – это геометрическая фигура,
обладающая свойством самоподобия, т. е.
составленная из нескольких частей, каждая из
которых подобна всей фигуре в целом.
Термин был предложен Б. Мандельбротом
в 1975 году (книга «Фрактальная геометрия
природы»).
2

3. Виды фракталов

Классификация по способу построения,
предложенная Калге в 1988 г.:
Геометрические фракталы (наиболее
наглядные, с них началась история
фракталов в XIX веке);
Алгебраические фракталы;
Стохастические фракталы.
3

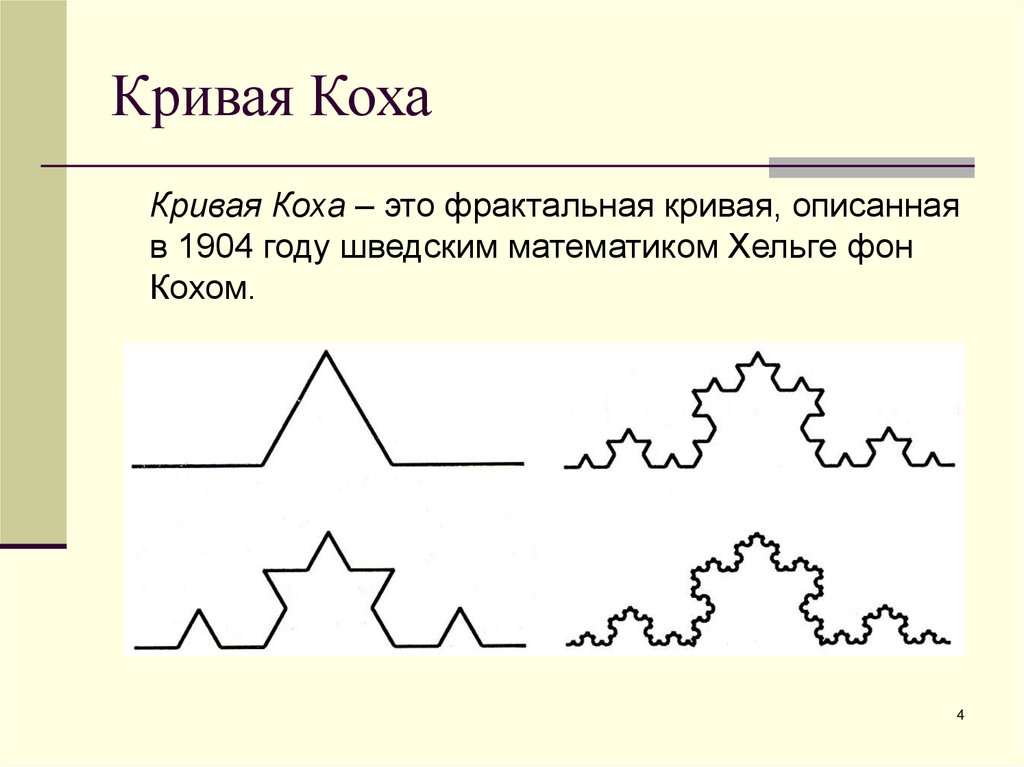
4. Кривая Коха

Кривая Коха – это фрактальная кривая, описанная
в 1904 году шведским математиком Хельге фон
Кохом.
4

5. «Снежинка» Коха

Исходная фигура
(ломаная линия)
называется
аттрактором или
генератором.
Геометрическими
парадоксами снежинки
Коха являются ее
бесконечная длина и то,
что к любой точке этого
фрактала невозможно
провести касательную.
5

6. Кривая Минковского

6

7. Итеративные системы функций

К геометрическим фракталам также относят
фракталы, получаемые с помощью
«итеративных систем функций» (Iterated
Function System), например папоротник
Барнсли, ковер Серпинского, дерево Пифагора, квадрат Кантора, губка Менгера и т. д.
Итеративные системы функций также
используются во фрактальной компрессии
изображений.
7

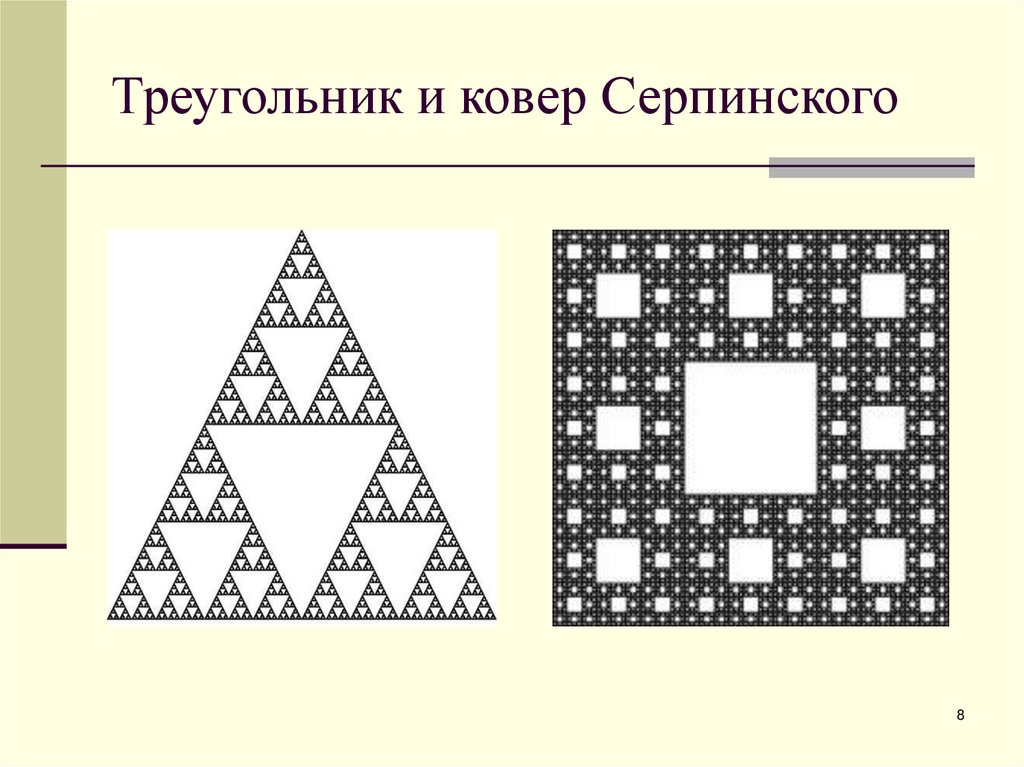
8. Треугольник и ковер Серпинского

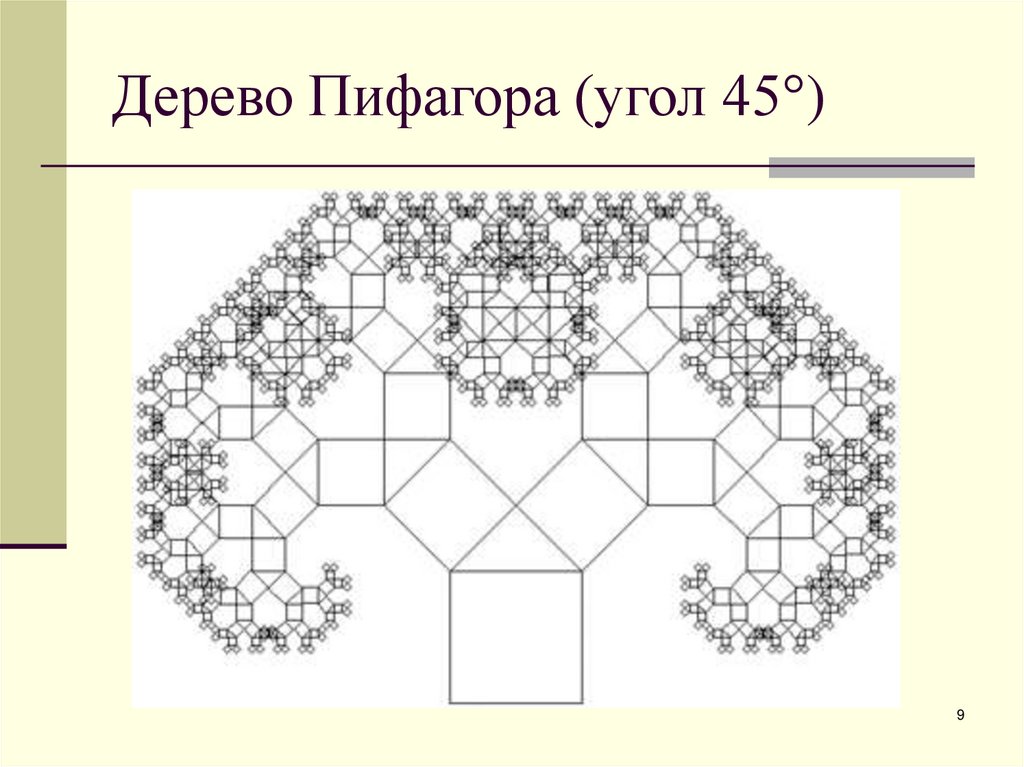
8

9. Дерево Пифагора (угол 45°)

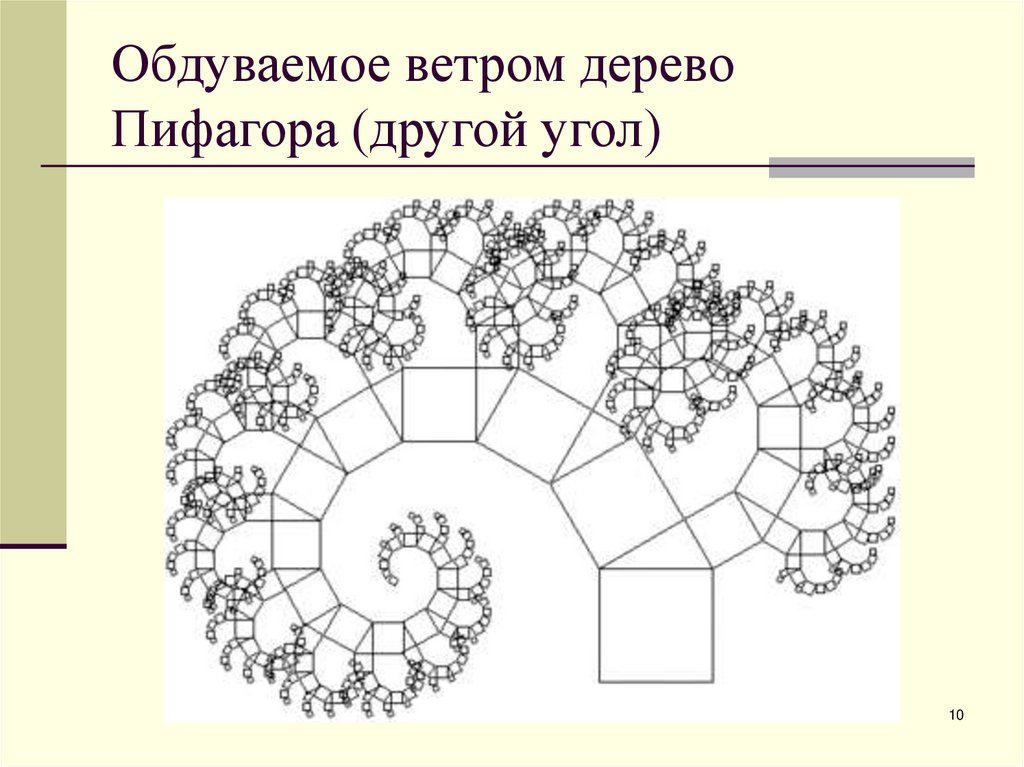
9

10. Обдуваемое ветром дерево Пифагора (другой угол)

10

11. Папоротник Барнсли и кривая дракона (Хартера-Хейтуэя)

11

12. Алгебраические фракталы

Это самая большая группа фракталов.
Получают их в процессе итераций функций
или систем функций. Наиболее известны
изображения множеств Мандельброта и
Жюлиа, получаемые при итерациях
комплексных многочленов второй степени.
На комплексной плоскости выбирается
прямоугольная область и на ней
фиксируется сетка – пиксельный растр
изображения.
12

13. Алгебраические фракталы

К числам-точкам применяется фрактальная
функция, которая переводит их в другие
числа. При большом числе итераций характер
поведения влияет на цвет выбранной точки:
сравниваются полученные значения с заранее
выбранным числом. Несмотря на
примитивность алгоритма и используемых
функций, получаемые изображения весьма
нетривиальны.
13

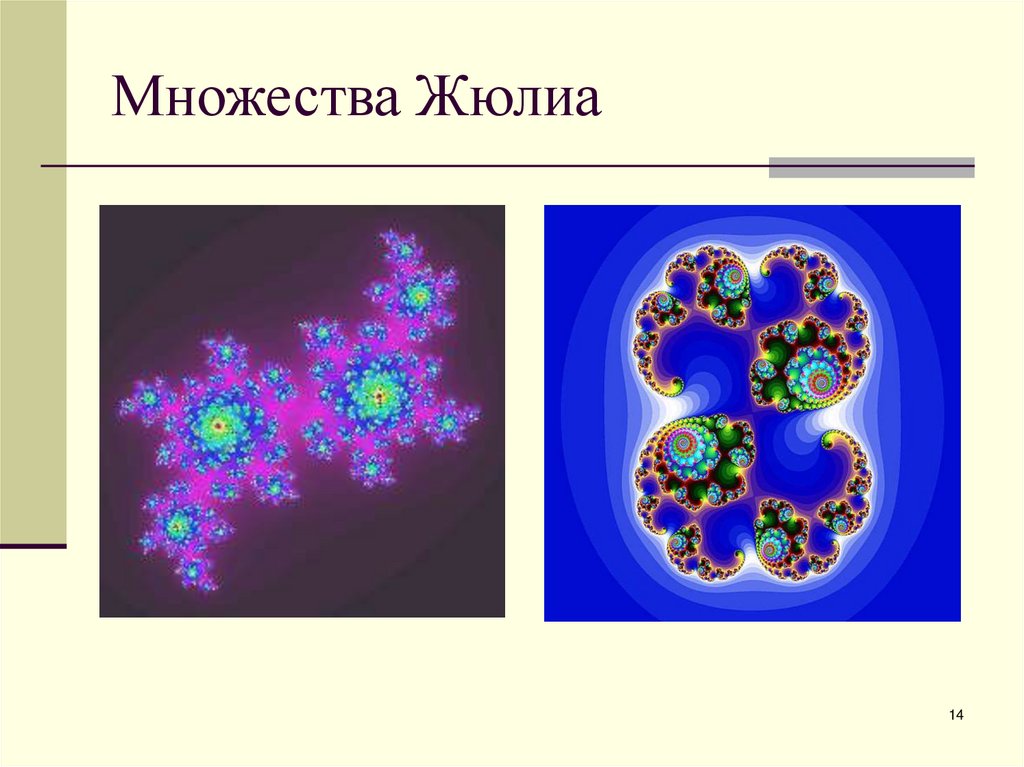
14. Множества Жюлиа

14

15. Стохастические фракталы

Фракталы, при построении которых в
итеративной системе случайным образом
изменяются какие-либо параметры,
называются стохастическими. В
компьютерной графике при получении
изображений деревьев, кустов, горной
местности или береговой линии в фракталы
добавляют случайные возмущения,
повышающие реалистичность синтезируемых
объектов.
15

16. Фрактальная форма цветной капусты

16