Лекция 10. Множества. Функции. Ч.1

1. Множества. Функции.

Лекция №10 ЧАСТЬ 1
1

2.

МНОЖЕСТВО ЕСТЬ
МНОГОЕ,
МЫСЛИМОЕ КАК
ЕДИНОЕ
1845 г. – 1918 г.
(Георг Кантор)
2

3. ПЛАН ЛЕКЦИИ

Понятие множества
Кортежи
Прямое произведение множеств
Проекции множеств
Соответствия
Свойства соответствий
3

4. Общие положения Теории множеств

Теория множеств — одна из самых молодых математических
дисциплин.
Ее появление связано с работами немецкого математика Георга Кантора,
опубликованными в 1874—1884 годах. Определение множества по
Кантору: “объединение в одно целое хорошо различаемых объектов
нашей интуиции или мысли”. Понятие множества оказалось настолько
общим и в то же время полезным, что многие сложные конструкции
алгебры, геометрии и математического анализа получили ясное
теоретико-множественное описание. Это сделало теорию множеств
универсальным математическим языком. В настоящее время теория
множеств — активно развивающаяся область математики.
4

5. Определение множества

Под множеством понимается совокупность (набор) некоторых объектов (элементов,
точек). Множества мы будем обозначать большими буквами ( A , B , X , Y ), его элементы
— малыми ( a, b, x, y ). Тот факт, что a является элементом множества A , будем обозначать
a ∈ A (читается: a принадлежит множеству A ).
Множества могут быть конечными и бесконечными.
Для задания определенного множества A надо указать те элементы, которые ему
принадлежат.
Это можно сделать несколькими способами, например:
перечислением элементов: A = {a1, a2, ...an};
заданием характеристического свойства: B = {x|x ∈ N, четное};
порождающей процедурой: F = {xk|x0 = 0, x1 = 1, xk = xk−2 + xk−1}.
5

6. Операции над множествами и их свойства

УНИВЕРСАЛЬНОЕ МНОЖЕСТВО. Часто рассматривают
множества какого-то определенного типа, т.е. все они
одновременно содержатся в некотором “большом”
множестве. Такое множество, которое содержит все
рассматриваемые множества данного типа, называется
универсальным для этого типа множеством. Так, для
четырехугольников универсальным множеством является
плоскость, для числовых множеств — множество всех
вещественных чисел R и т.п. Обозначаются через I или U.
УНИВЕРСАЛЬНЫМ называют также гипотетическое
множество, которое должно включать в себя все
возможные компоненты. Однако такое всеохватывающее
множество противоречит самой сути понятия множества.
6

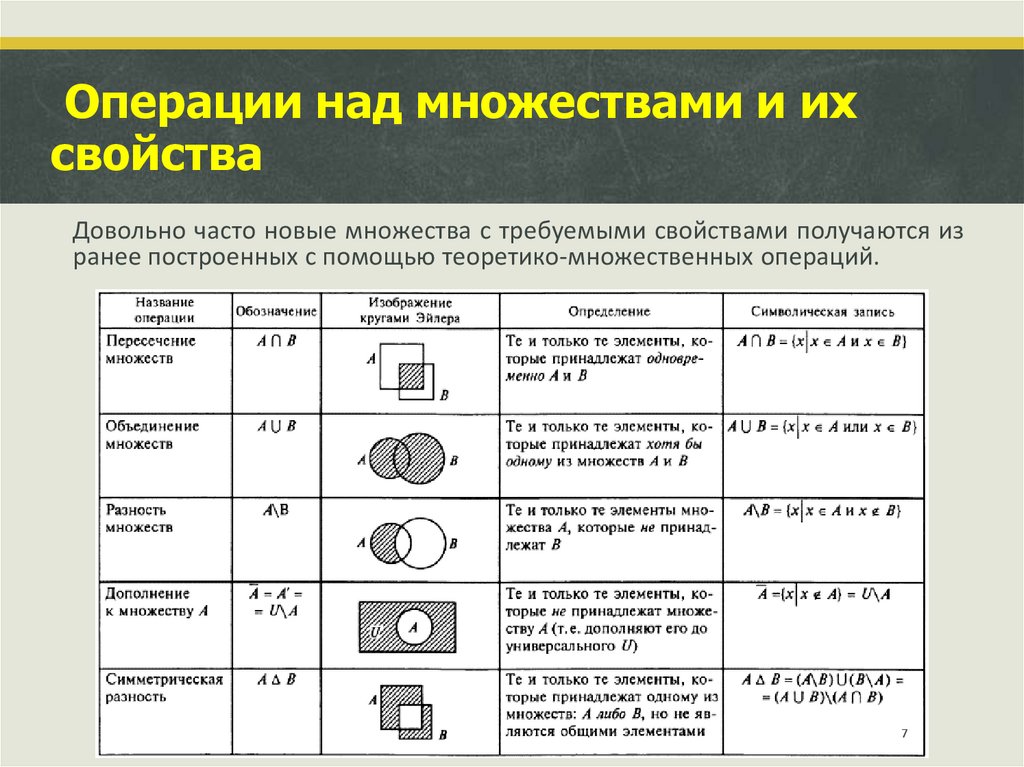
7. Операции над множествами и их свойства

Довольно часто новые множества с требуемыми свойствами получаются из
ранее построенных с помощью теоретико-множественных операций.
7

8. Кортежи. Декартовы произведения

В повседневной жизни и математике нам часто
приходится
иметь
дело
с
упорядоченными
множествами — кортежами.
Слово кортеж переводится с французского cortege
как
торжественная
процессия
(например,
свадебный кортеж).
8

9.

Треугольник АВС на плоскости задается
кортежем из 6 чисел
Где
— координаты вершин.
Слова в предложении, буквы в слове,
предложения в тексте — все это примеры
кортежей.
Двоичный
код
является
кортежем,
состоящим из цифр 0 и 1.
9

10.

В отличие от элементов множества
элементы кортежа могут совпадать.
Например, в прямоугольной системе
координат координаты точек являются
кортежами.
Операция, с помощью которой из двух
кортежей длиной k и m можно составить
новый кортеж длиной k + m, в котором
сначала идут подряд элементы первого
кортежа, а затем – элементы второго
кортежа,
называется
соединением
кортежей.
10

11. Декартово (прямое) произведение

ОПРЕДЕЛЕНИЕ:
Декартово произведение множеств – это
множество, элементами которого являются
всевозможные упорядоченные пары элементов
исходных двух множеств.
Данное понятие употребляется не только в
теории множеств, но также в алгебре,
топологии и прочих разделах математики
благодаря тому, что прямое произведение
часто наследует структуры (алгебраические,
топологические и т. д.), существующие на
перемножаемых множествах.
11

12. Декартово (прямое) произведение

Записывают декартово произведение множеств так:
A × B = {(a; b) | a ∈ A, b ∈ B}.
Это значит, что если например дано множество A =
{1,2,3} и множество B = {15,25}, то их декартово
произведение будет состоять из пар:
A × B = {(1;15), (1;25), (2;15), (2;25), (3;15), (3;25)}
Если во множестве A количество элементов равно m,
а во множестве B — n, то их декартово произведение
будет состоять из m×n элементов.
Следует иметь в виду что A×B и B×A разные
множества, так как пары типа (a; b) отличаются от
пар тип (b; a).
12

13.

Если множества
конечны, то их декартово произведение может быть
представлено в общем виде таблицей из m столбцов и
к строк.
Например, декартово произведение X х Y, где
можно представить в виде табл.
13

14.

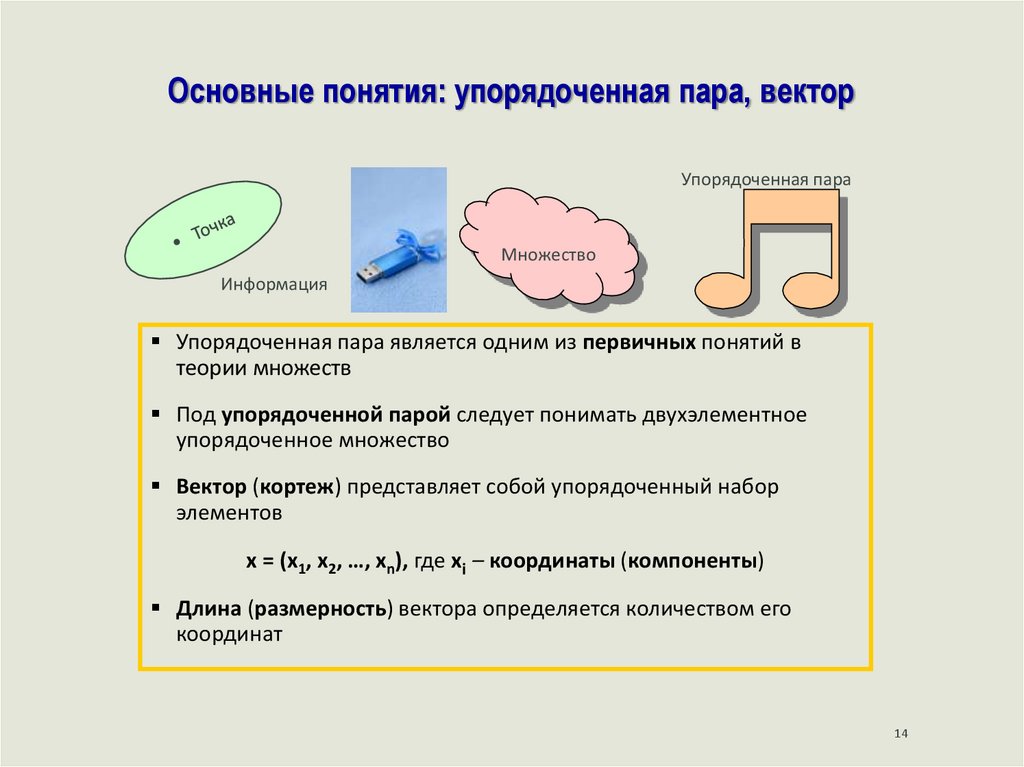
Основные понятия: упорядоченная пара, вектор
Упорядоченная пара
Множество
Информация
Упорядоченная пара является одним из первичных понятий в
теории множеств
Под упорядоченной парой следует понимать двухэлементное
упорядоченное множество
Вектор (кортеж) представляет собой упорядоченный набор
элементов
х = (х1, х2, …, хn), где хi – координаты (компоненты)
Длина (размерность) вектора определяется количеством его
координат
14

15.

Проекция вектора на ось
Два вектора x, y одинаковой размерности
равны, если их соответствующие компоненты
равны:
x=y i xi=yi
проекцией вектора х=(х1, х2, …, хn) на i-ю
ось называется его i-й компонент Pr i x = хi
пусть V – множество векторов одинаковой
длины, тогда проекцией множества V на i-ю
ось называется множество проекций всех
векторов из V: Pri V Pri v | v V
15

16.

Примеры
Координаты точки плоскости
образуют упорядоченную пару: на
первой позиции – абсцисса, на
второй – ордината. Они являются
проекциями на первую и вторую оси
соответственно
y
y1
0
Дано множество V векторов
размерности 3:
(x1, y1)
x1
Pr1V={a,c,b}
Pr2V={b}
Pr3V={c,d}
V = { (a,b,c), (c,b,d), (b,b,d) }
Найти проекции множества V на оси
16
x

17.

Соответствия
соответствие – подмножество декартова
произведения двух множеств:
G A B
А – область определения (множество
отправления) соответствия G :
Pr1G={ x | (x,y) G }
В – область значений (множество прибытия)
соответствия G :
Pr2G={ y | (x,y) G }
17

18.

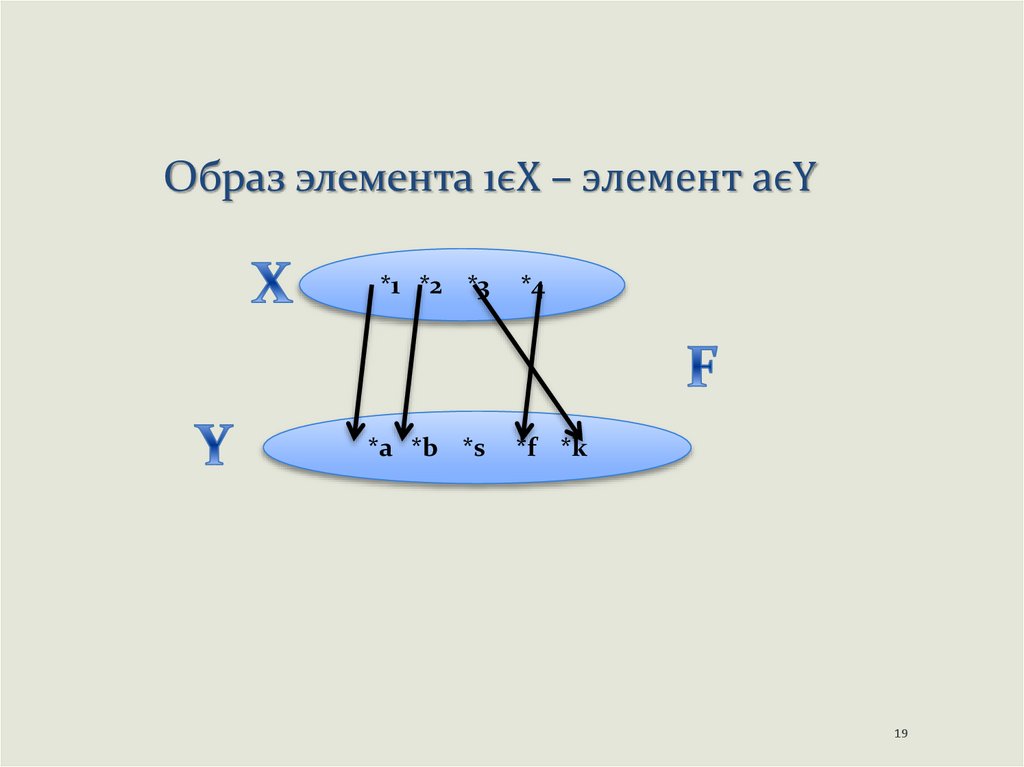
Образы и прообразы
множество всех элементов y B, соответствующих
элементу x A, называется образом элемента х в
множестве B при соответствии G.
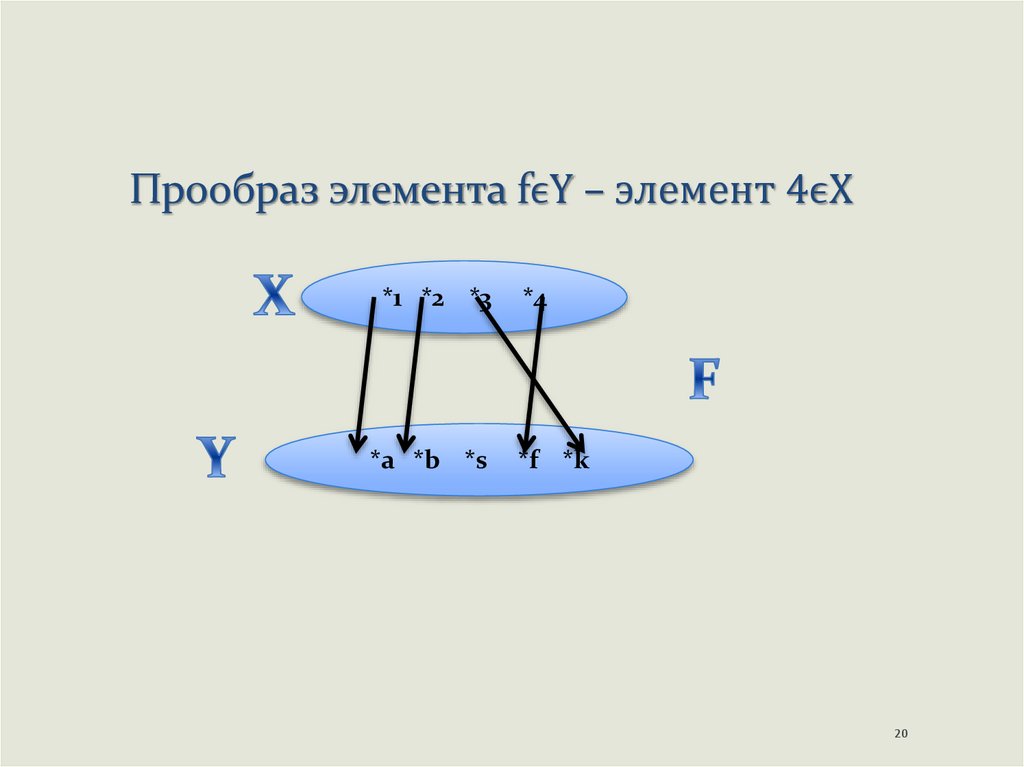
множество всех элементов x A, которым соответствует
элемент y B, называется прообразом элемента y в
множестве A при соответствии G.
18

19.

Образ элемента 1ϵX – элемент аϵY
*1 *2 *3
*4
*a *b *s
*f *k
19

20.

Прообраз элемента fϵY – элемент 4ϵX
*1 *2 *3
*4
*a *b *s
*f *k
20

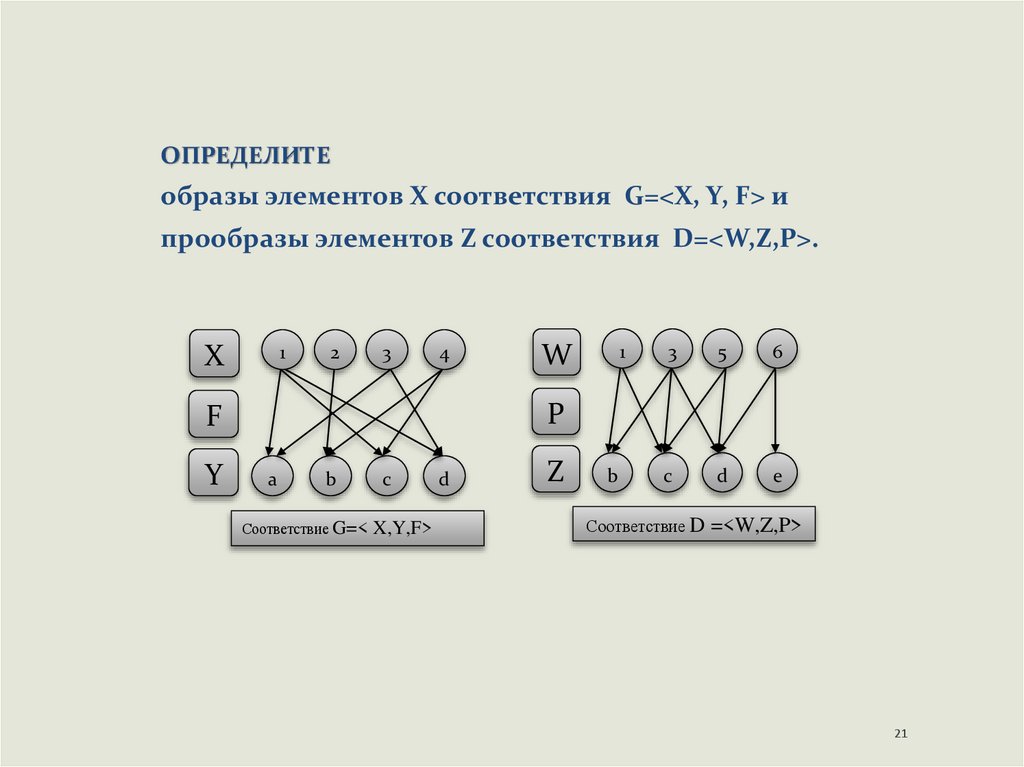
21.

ОПРЕДЕЛИТЕ
образы элементов Х соответствия G=<Х, Y, F> и
прообразы элементов Z соответствия D=<W,Z,P>.
X
1
2
3
4
1
3
5
6
c
d
e
P
F
Y
W
a
b
c
Соответствие G=< X,Y,F>
d
Z
b
Соответствие D =<W,Z,P>
21

22. ГРАФЫ

Графом называется система объектов
произвольной природы (вершин) и связок
(ребер), соединяющих некоторые пары
этих объектов.
22

23. Основные свойства соответствий

23

24.

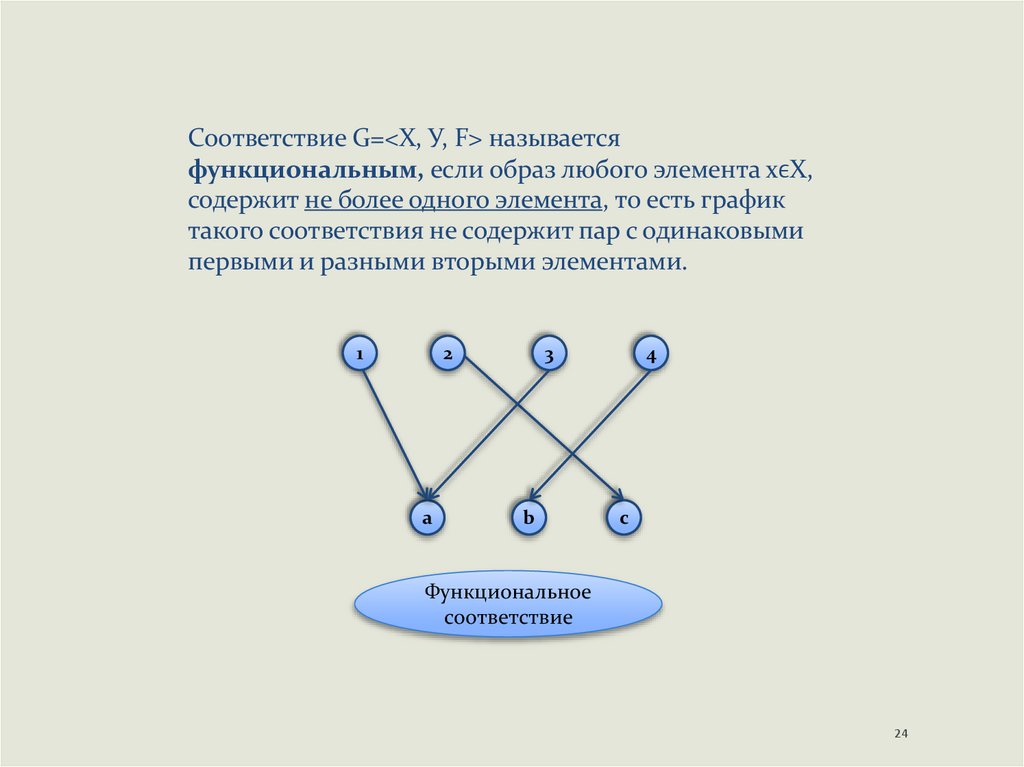
Соответствие G=<Х, У, F> называется
функциональным, если образ любого элемента хϵХ,
содержит не более одного элемента, то есть график
такого соответствия не содержит пар с одинаковыми
первыми и разными вторыми элементами.
1
2
a
3
b
4
c
Функциональное
соответствие
24

25.

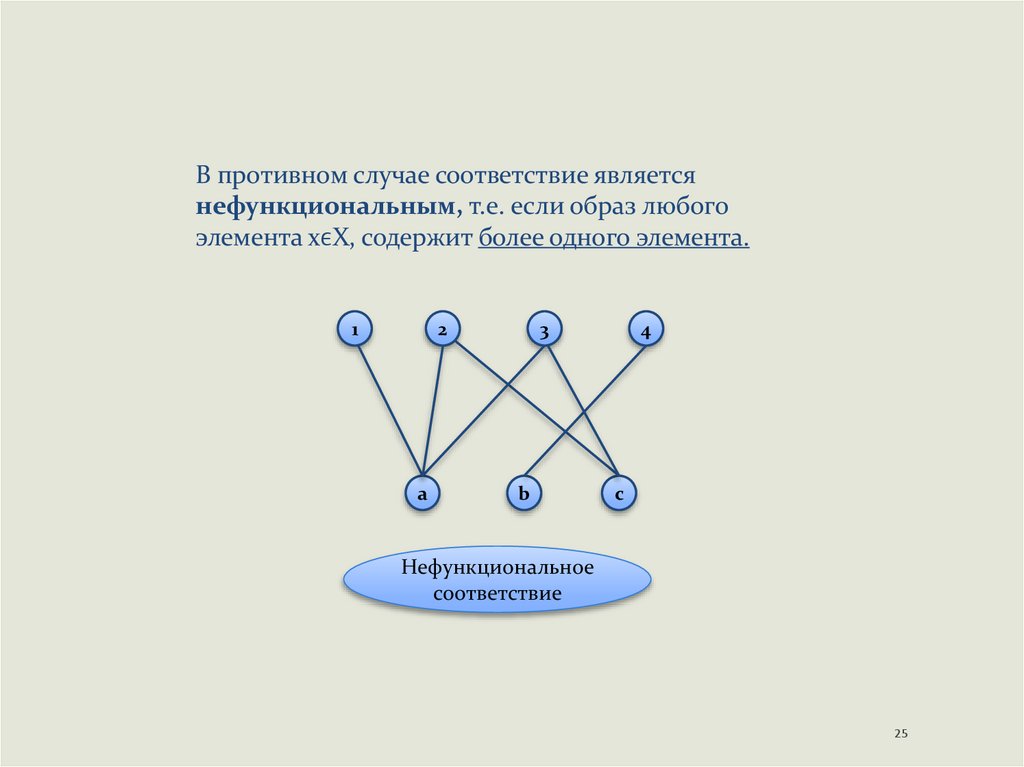
В противном случае соответствие является
нефункциональным, т.е. если образ любого
элемента хϵХ, содержит более одного элемента.
1
2
a
3
b
4
c
Нефункциональное
соответствие
25

26.

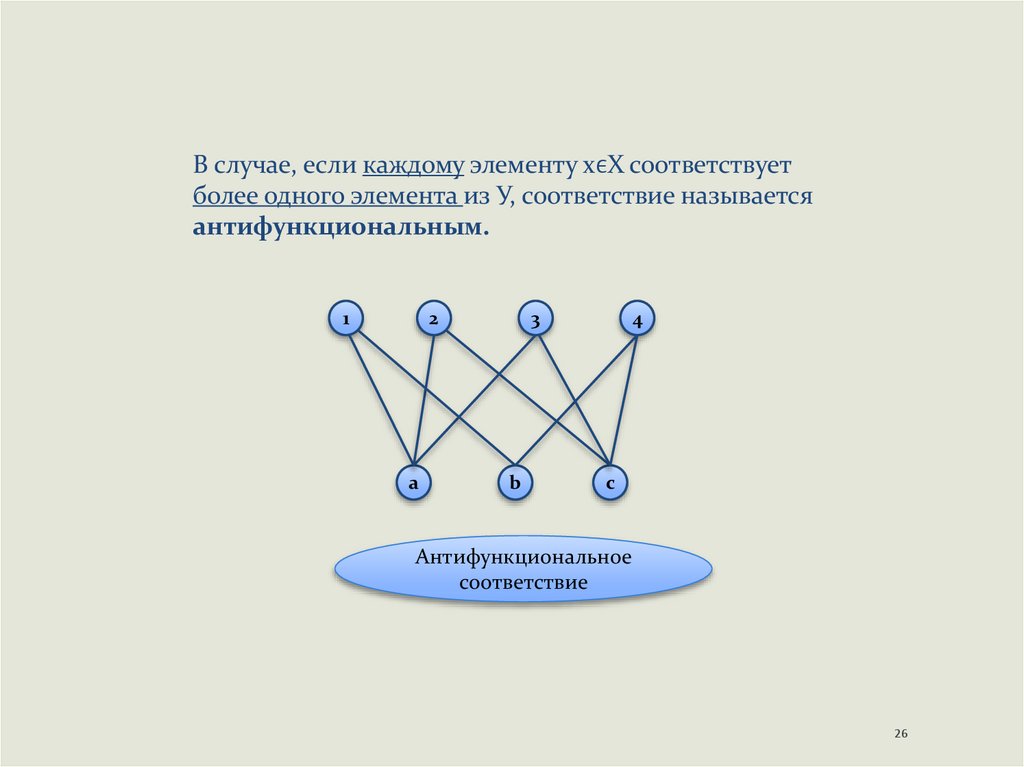
В случае, если каждому элементу хϵХ соответствует
более одного элемента из У, соответствие называется
антифункциональным.
1
2
a
3
b
4
c
Антифункциональное
соответствие
26

27.

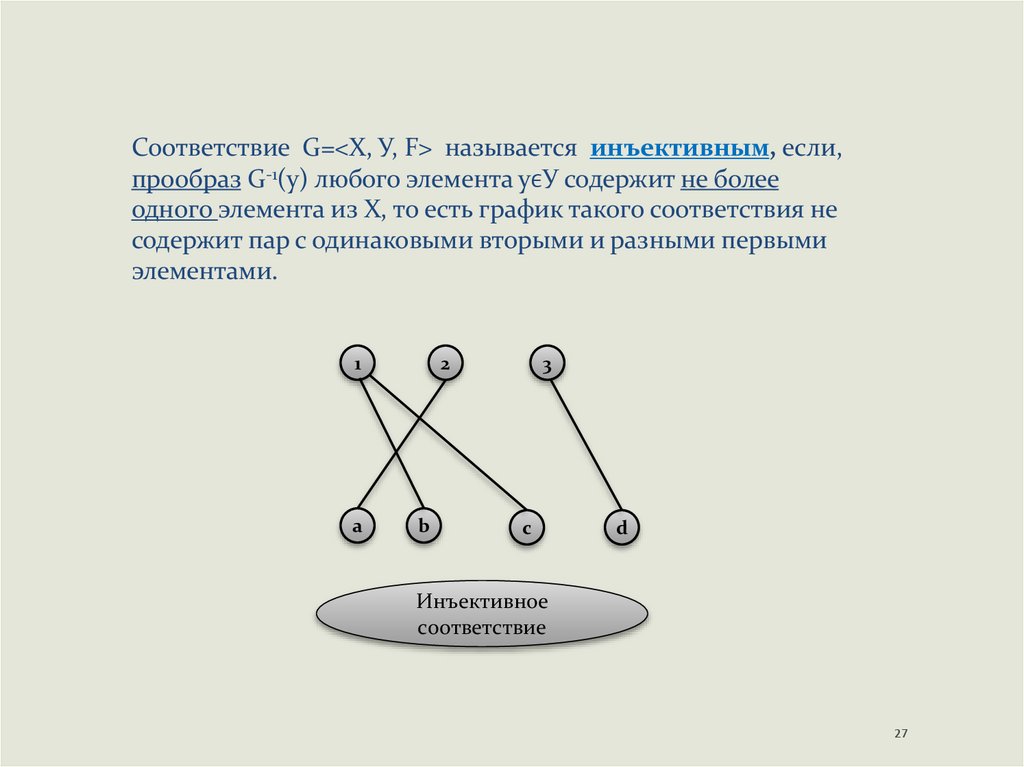
Соответствие G=<Х, У, F> называется инъективным, если,
прообраз G-1(у) любого элемента уϵУ содержит не более
одного элемента из X, то есть график такого соответствия не
содержит пар с одинаковыми вторыми и разными первыми
элементами.
1
a
2
b
3
c
d
Инъективное
соответствие
27

28.

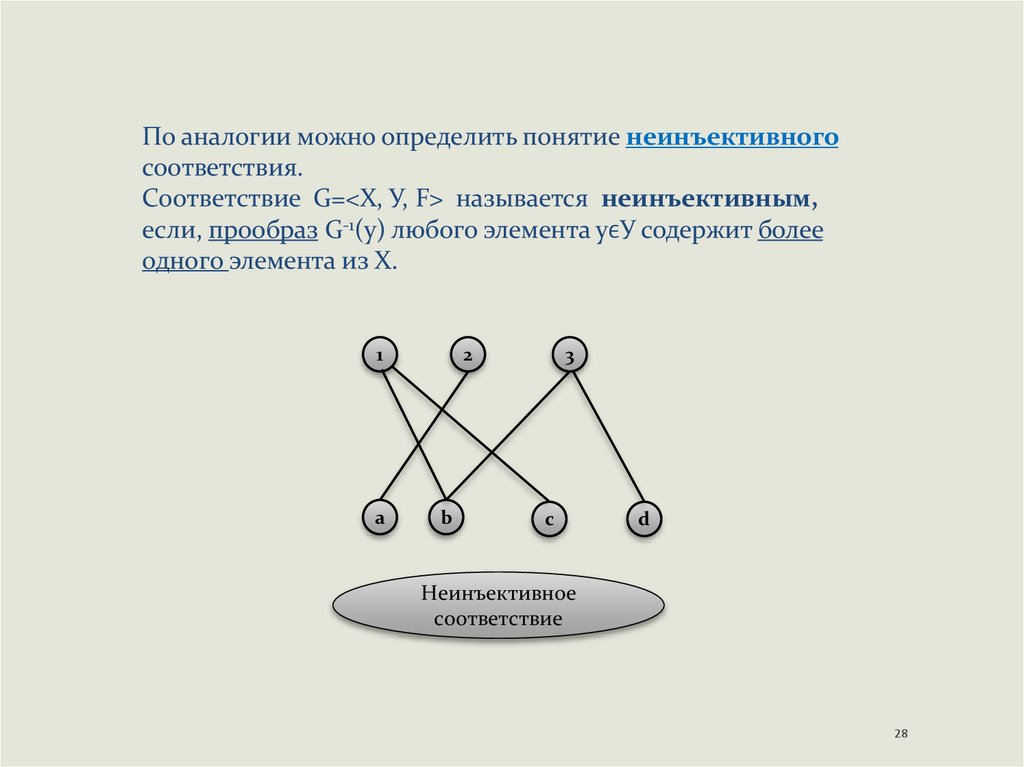
По аналогии можно определить понятие неинъективного
соответствия.
Соответствие G=<Х, У, F> называется неинъективным,
если, прообраз G-1(у) любого элемента уϵУ содержит более
одного элемента из X.
1
a
2
b
3
c
d
Неинъективное
соответствие
28

29.

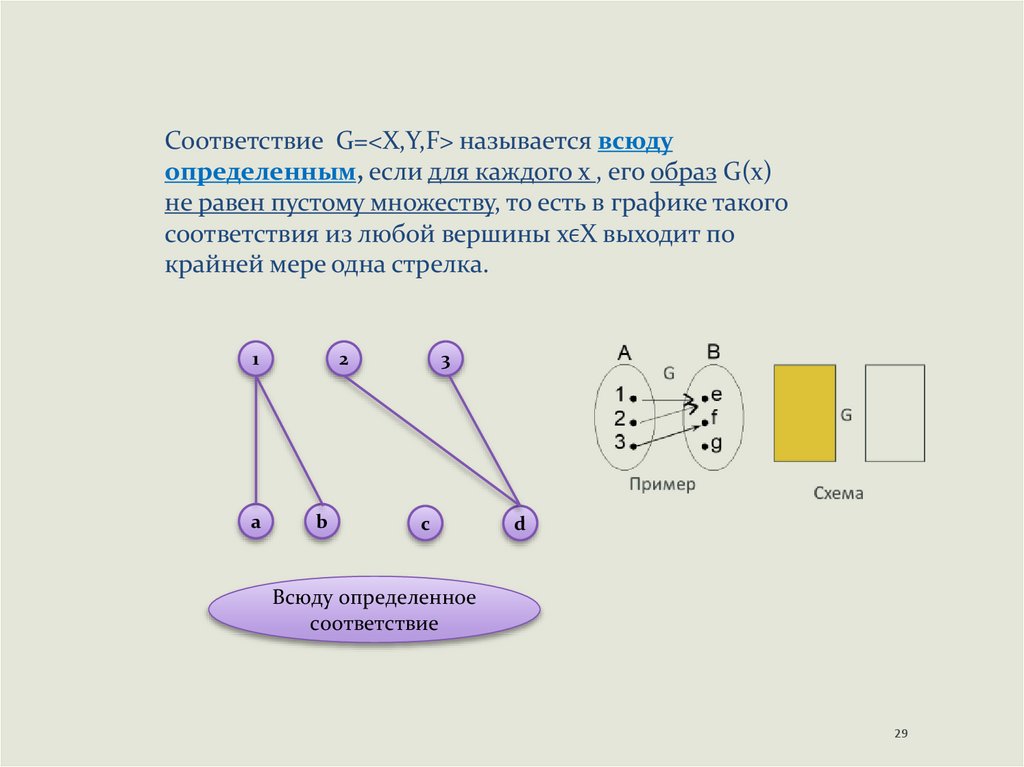
Соответствие G=<X,Y,F> называется всюду
определенным, если для каждого х , его образ G(х)
не равен пустому множеству, то есть в графике такого
соответствия из любой вершины хϵX выходит по
крайней мере одна стрелка.
1
a
2
b
3
c
d
Всюду определенное
соответствие
29

30.

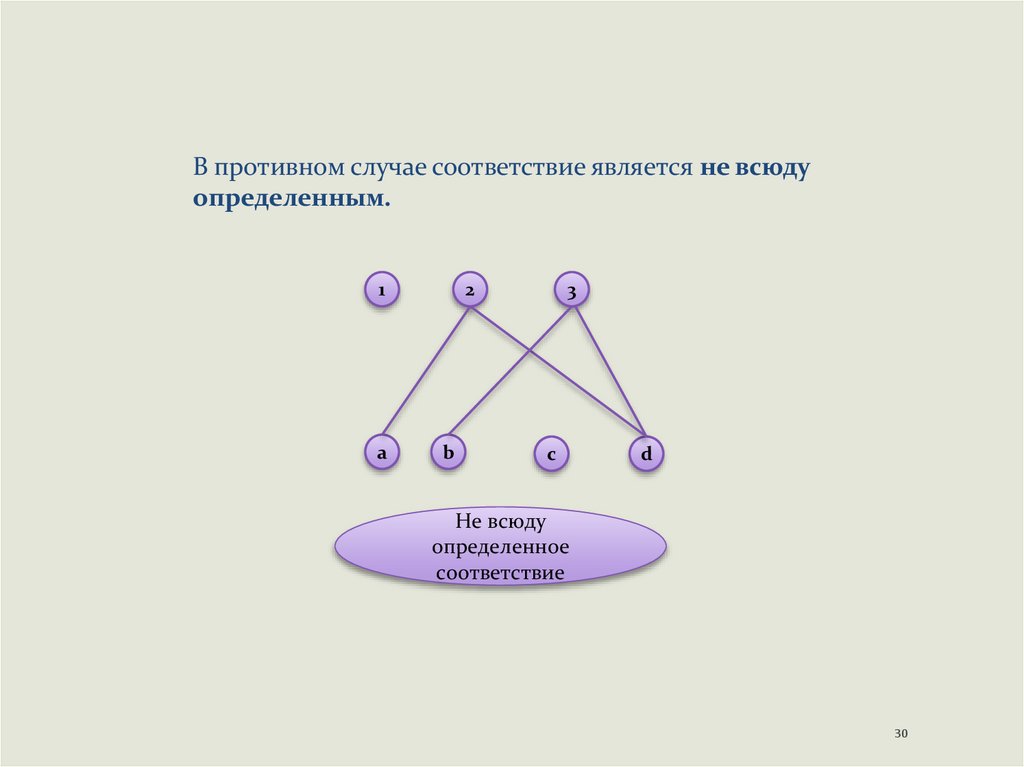
В противном случае соответствие является не всюду
определенным.
1
a
2
b
3
c
d
Не всюду
определенное
соответствие
30

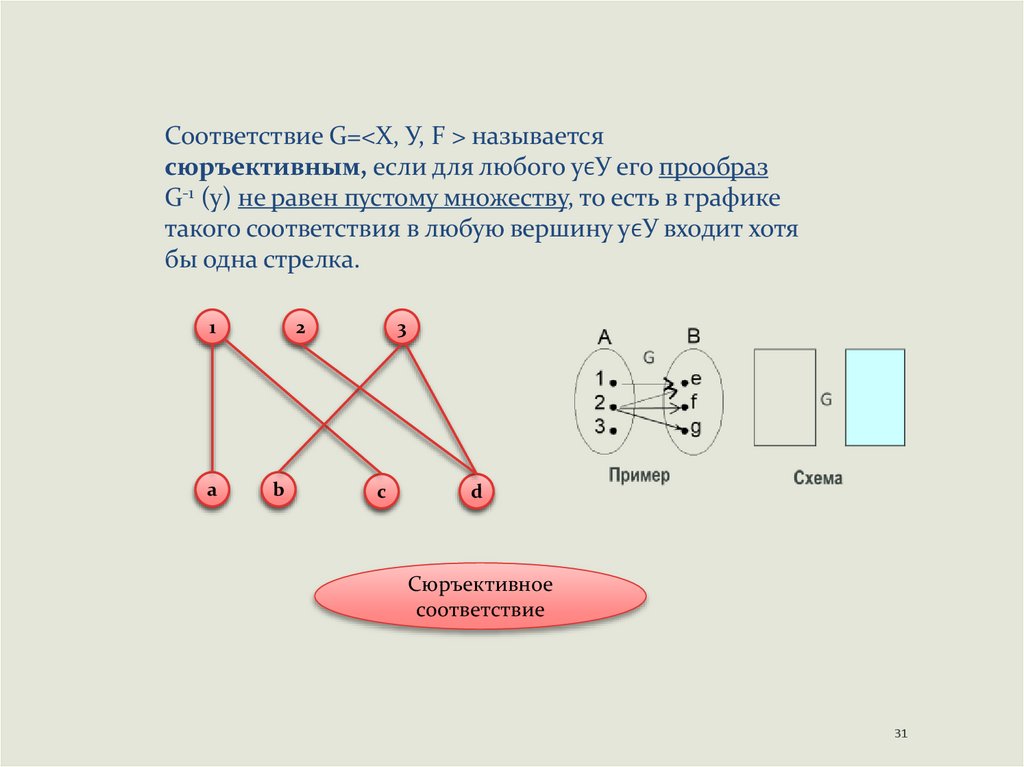
31.

Соответствие G=<Х, У, F > называется
сюръективным, если для любого уϵУ его прообраз
G-1 (у) не равен пустому множеству, то есть в графике
такого соответствия в любую вершину уϵУ входит хотя
бы одна стрелка.
1
a
2
b
3
c
d
Сюръективное
соответствие
31

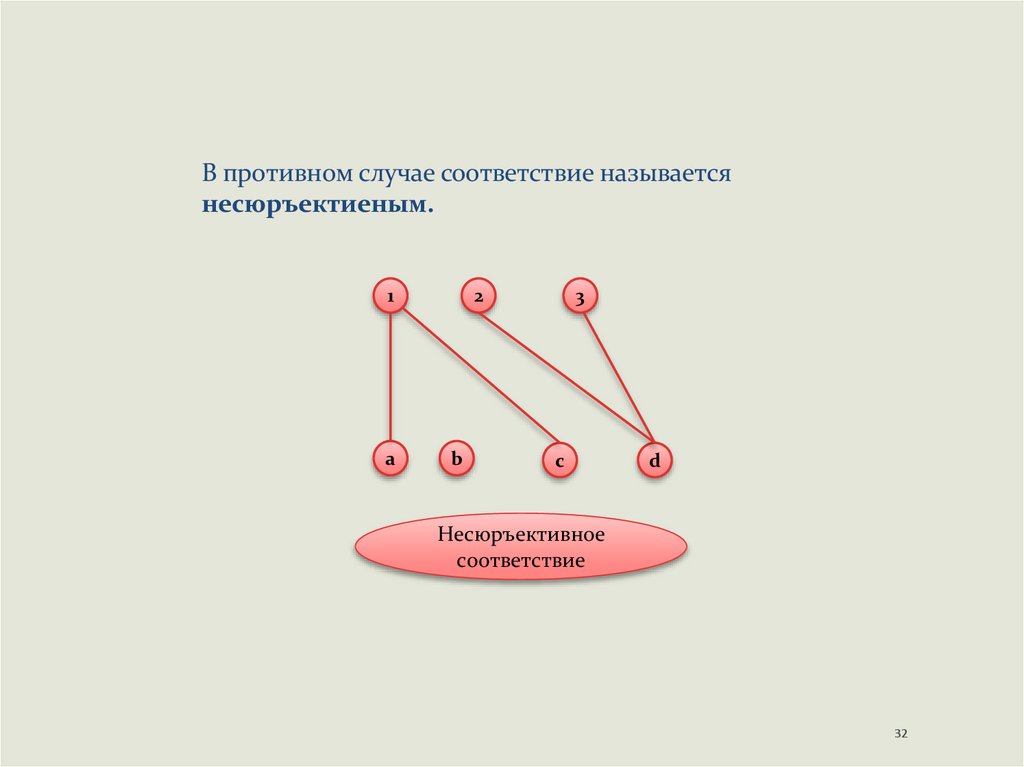
32.

В противном случае соответствие называется
несюръектиеным.
1
a
2
b
3
c
d
Несюръективное
соответствие
32

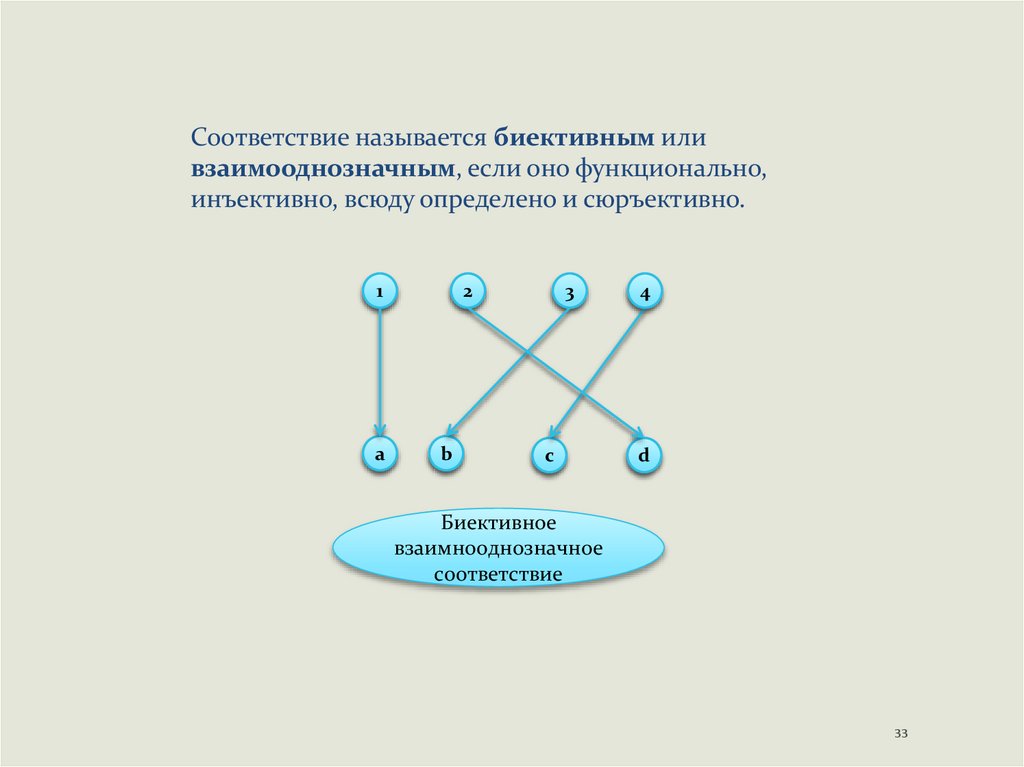
33.

Соответствие называется биективным или
взаимооднозначным, если оно функционально,
инъективно, всюду определено и сюръективно.
1
a
2
b
3
c
4
d
Биективное
взаимнооднозначное
соответствие
33

34. ПРИМЕР

Дано соответствие <P,X,Y>, где X - множество конфет, Y множество фантиков, P - ”быть упакованным в фантик”.
Какими свойствами обладает данное соответствие?
Данное соответствие
1. функциональное, так как две и более конфет не может
быть упаковано в один фантик;
2. инъективное, так как одна конфета не может быть
завернута в два фантика одновременно;
3. не всюду определенное, так как существуют сорта
конфет, которые продаются без фантиков (зефир,
мармелад);
4. сюръективное, так как фантики без конфет - это мусор
34

35.

X
1
3
F
Y
W
b
c
d
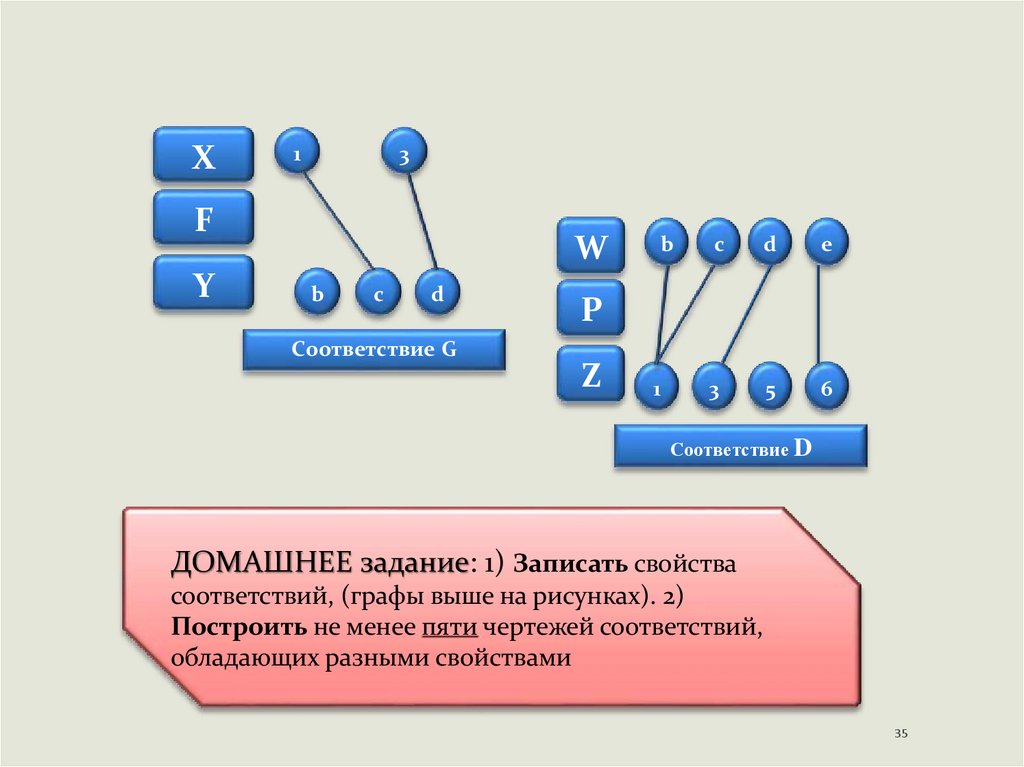
Соответствие G
b
c
d
e
1
3
5
6
P
Z
Соответствие D
ДОМАШНЕЕ задание: 1) Записать свойства
соответствий, (графы выше на рисунках). 2)
Построить не менее пяти чертежей соответствий,
обладающих разными свойствами
35