Похожие презентации:
Представление_логических_выражений_ppsx
1. Представление логических выражений
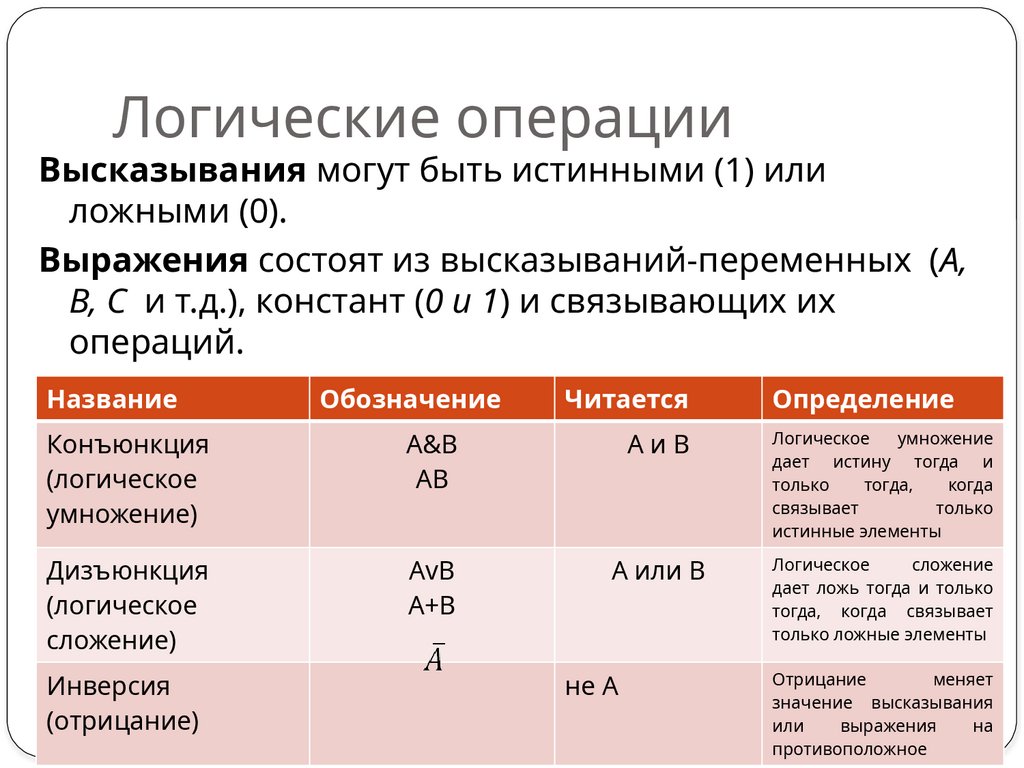
Множества и схемы2. Логические операции
Высказывания могут быть истинными (1) илиложными (0).
Выражения состоят из высказываний-переменных (A,
B, C и т.д.), констант (0 и 1) и связывающих их
операций.
Простейшие
логические
Название
Обозначениеоперации:
Читается
Определение
Конъюнкция
(логическое
умножение)
A&B
AB
AиB
Логическое
умножение
дает истину тогда и
только
тогда,
когда
связывает
только
истинные элементы
Дизъюнкция
(логическое
сложение)
AvB
A+B
A или B
Логическое
сложение
дает ложь тогда и только
тогда, когда связывает
только ложные элементы
Инверсия
(отрицание)
не A
Отрицание
меняет
значение высказывания
или
выражения
на
противоположное
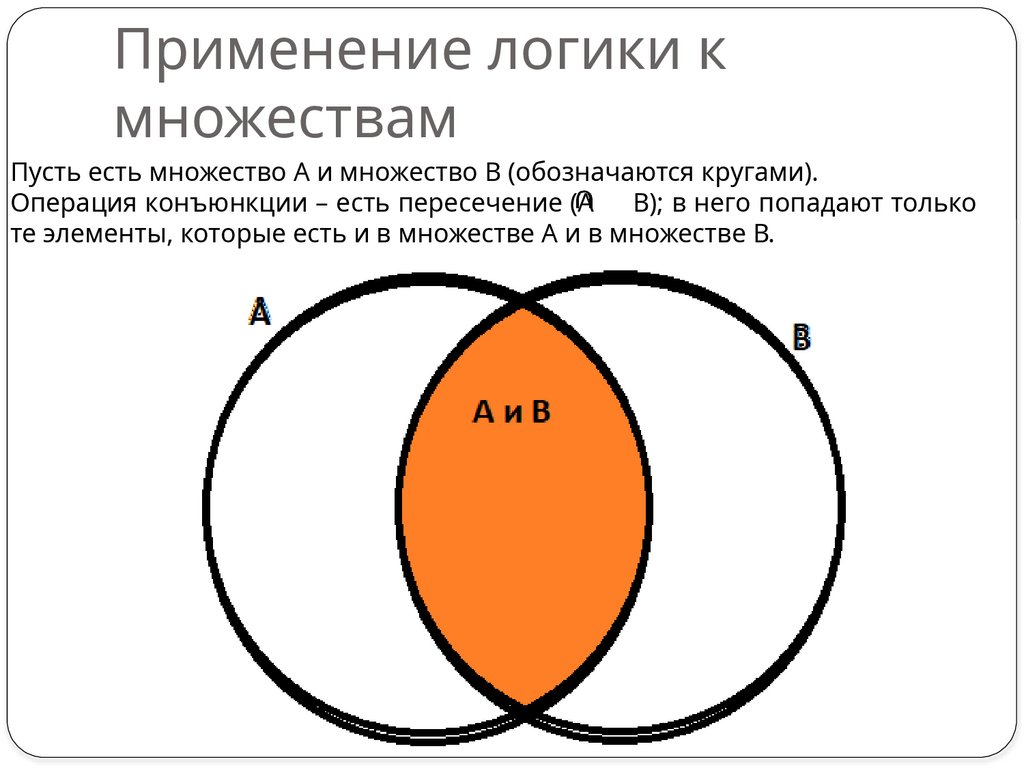
3. Применение логики к множествам
Пусть есть множество А и множество В (обозначаются кругами).Операция конъюнкции – есть пересечение (А
В); в него попадают только
те элементы, которые есть и в множестве А и в множестве В.
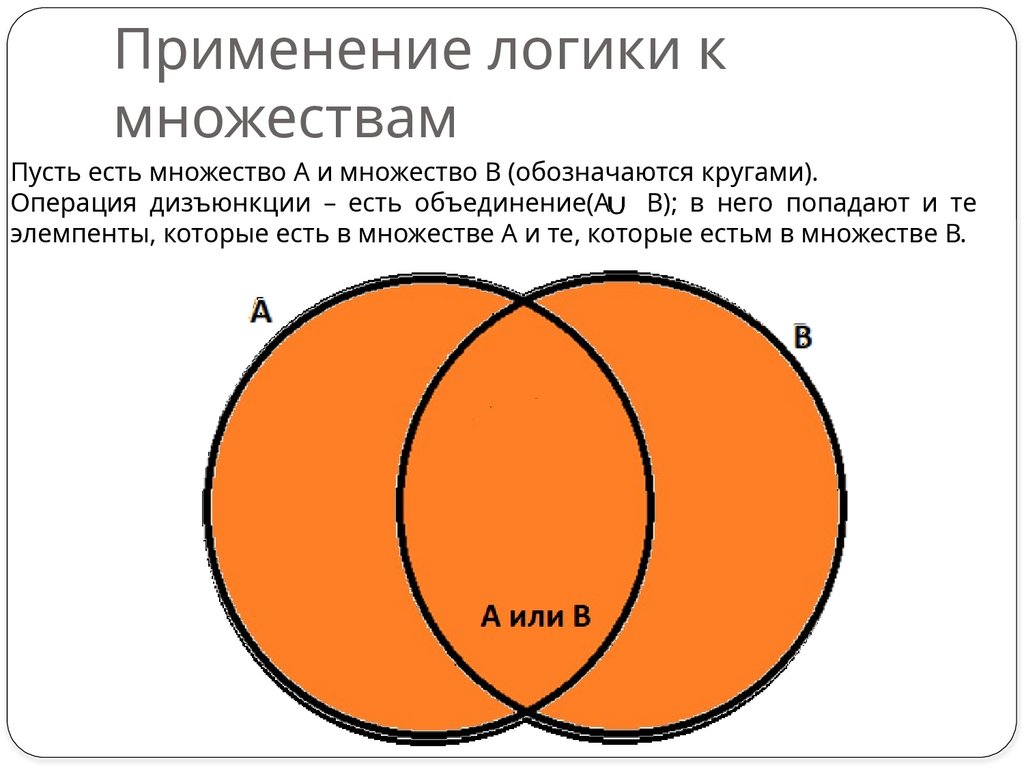
4. Применение логики к множествам
Пусть есть множество А и множество В (обозначаются кругами).Операция дизъюнкции – есть объединение(А В); в него попадают и те
элемпенты, которые есть в множестве А и те, которые естьм в множестве В.
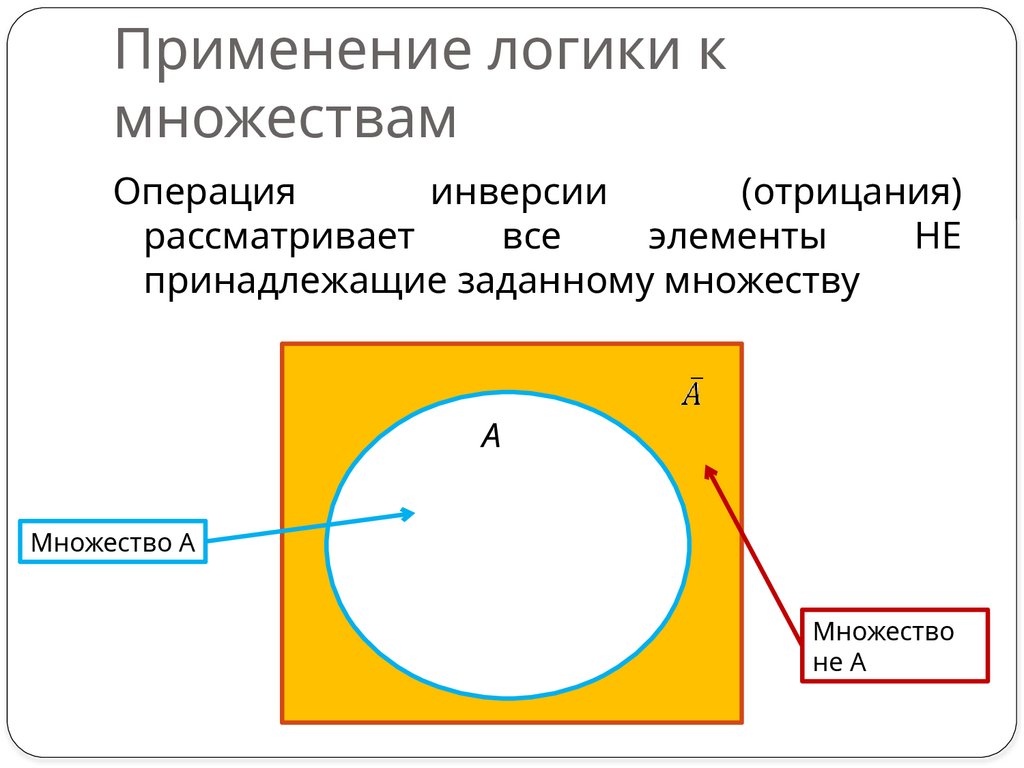
5. Применение логики к множествам
Операцияинверсии
(отрицания)
рассматривает
все
элементы
НЕ
принадлежащие заданному множеству
А
Множество А
Множество
не А
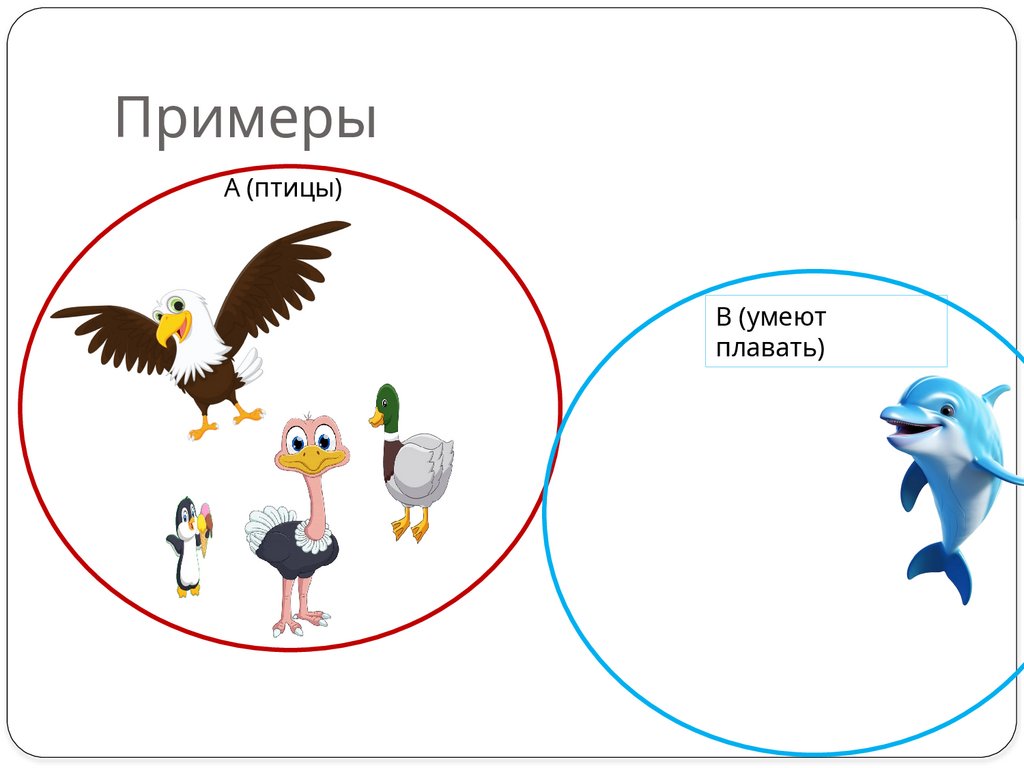
6. Примеры
А (птицы)В (умеют
плавать)
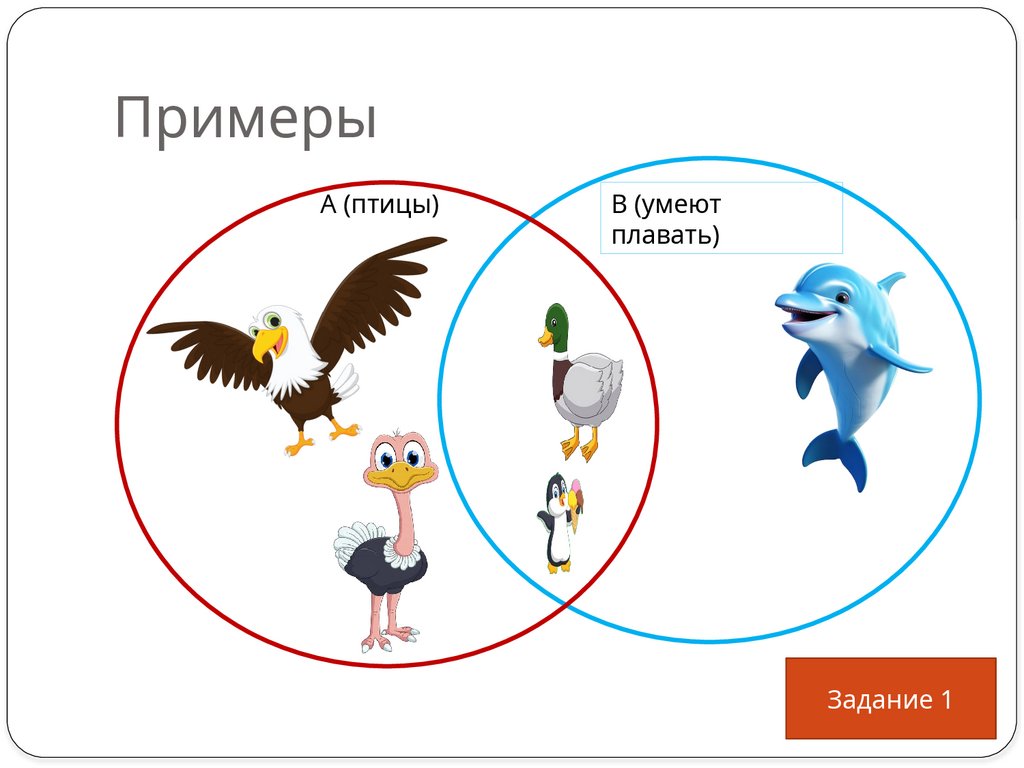
7. Примеры
А (птицы)В (умеют
плавать)
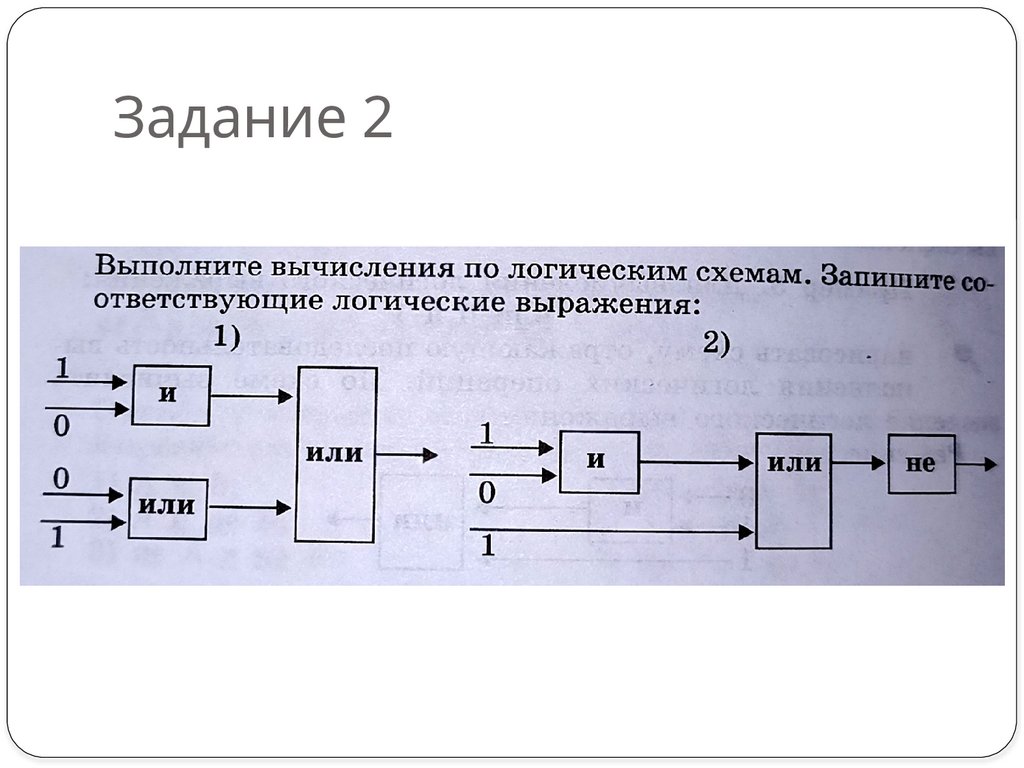
Задание 1
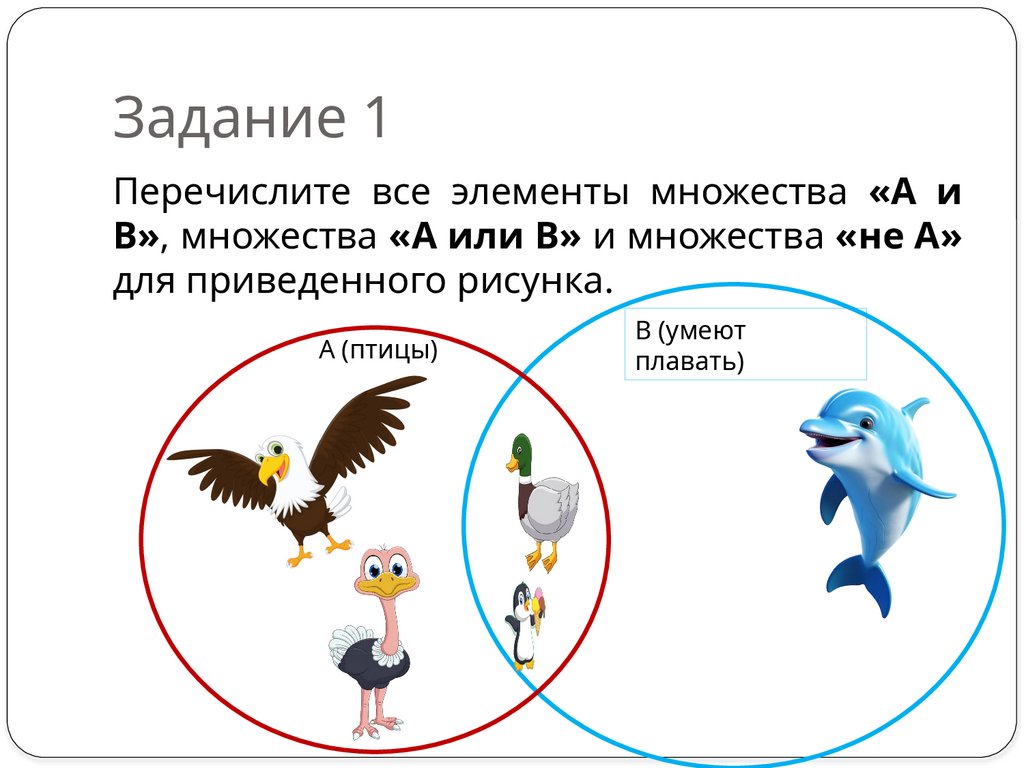
8. Задание 1
Перечислите все элементы множества «A иB», множества «А или В» и множества «не А»
для приведенного рисунка.
А (птицы)
В (умеют
плавать)
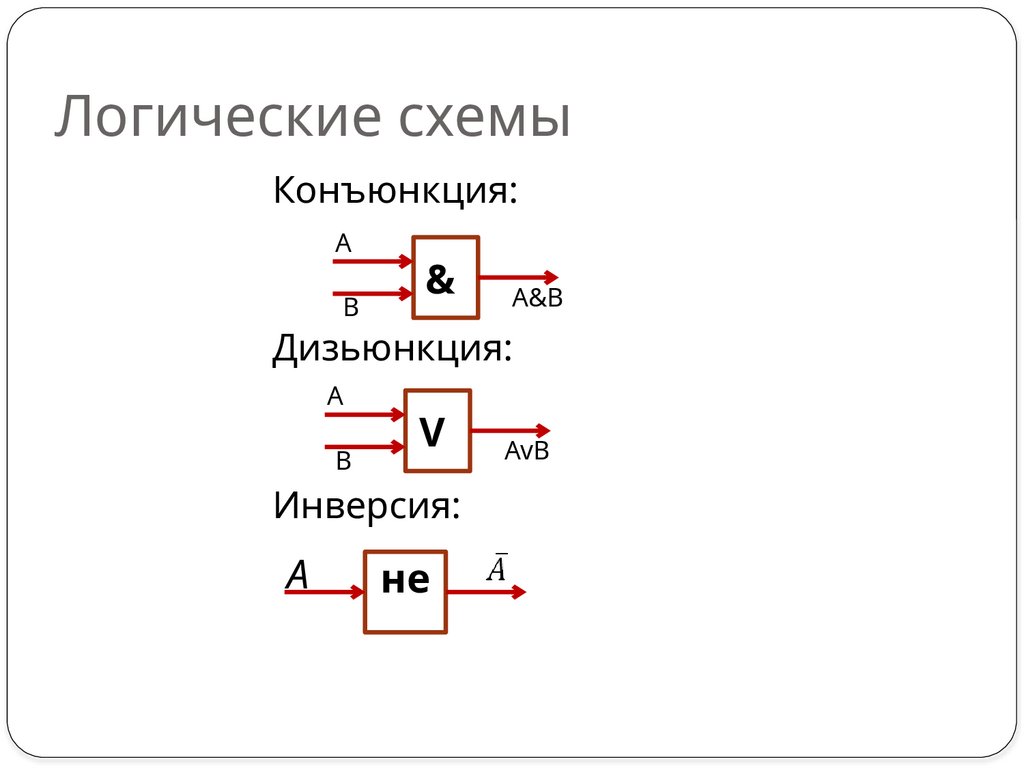
9. Логические схемы
Конъюнкция:А
&?
В
А&B
Дизьюнкция:
А
V?
В
Инверсия:
А
не
?
АvB
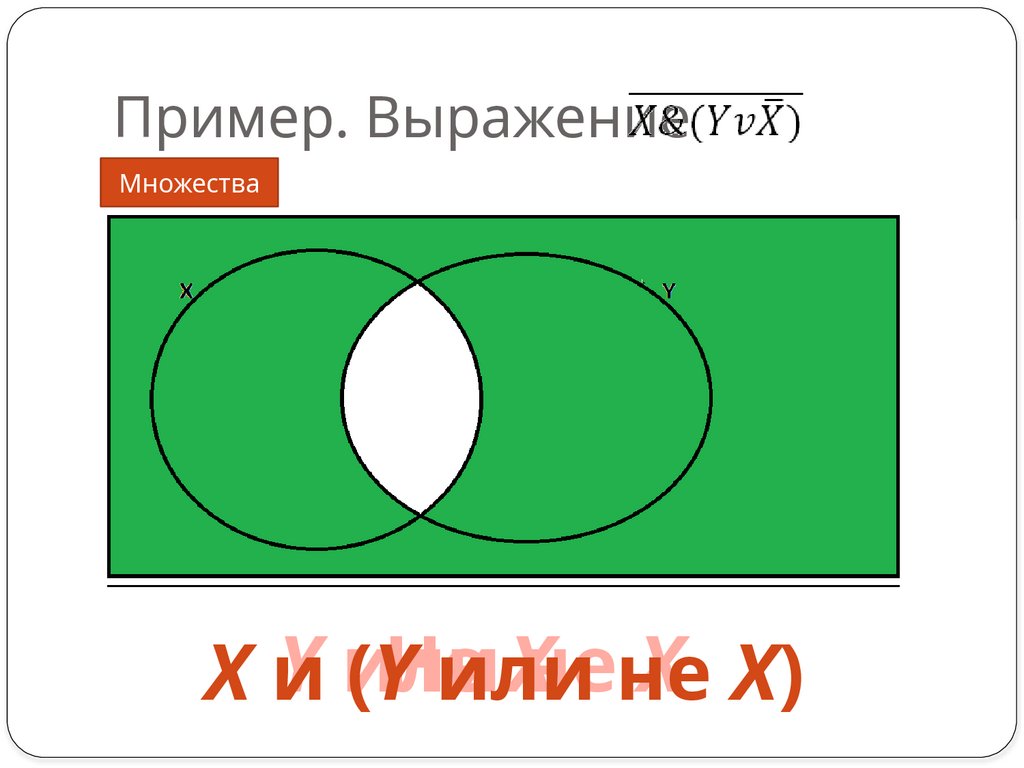
10. Пример. Выражение
МножестваY или
Xнене
X X)
Xи
(YНе
или
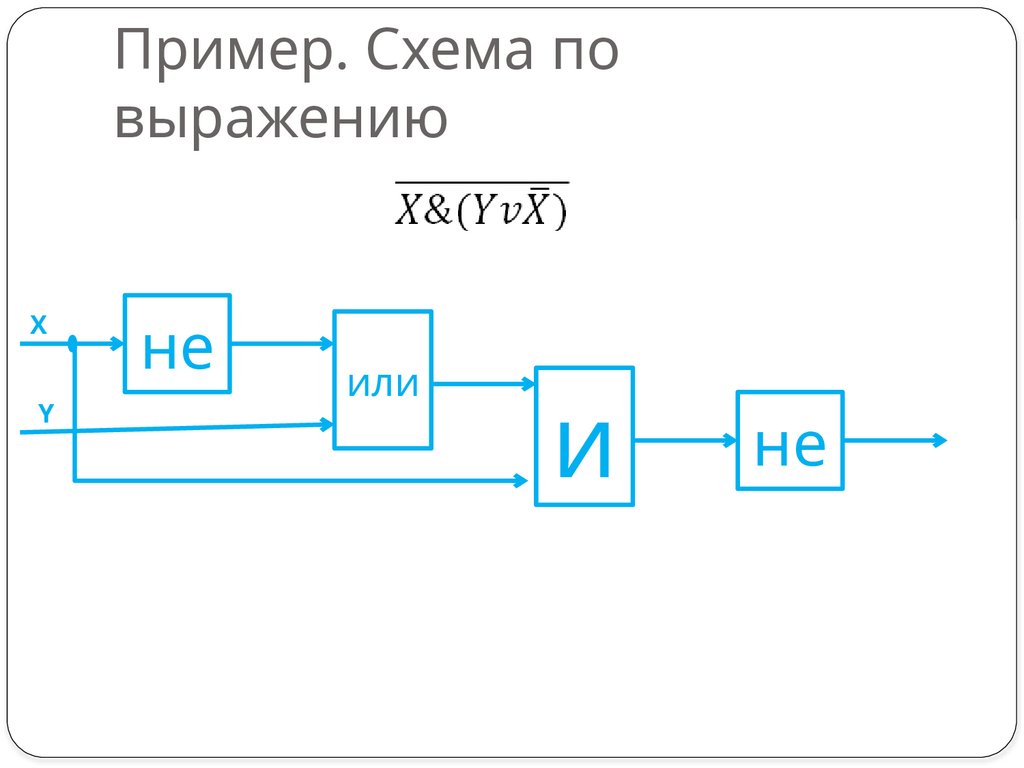
11. Пример. Схема по выражению
XY
не
или
и
не
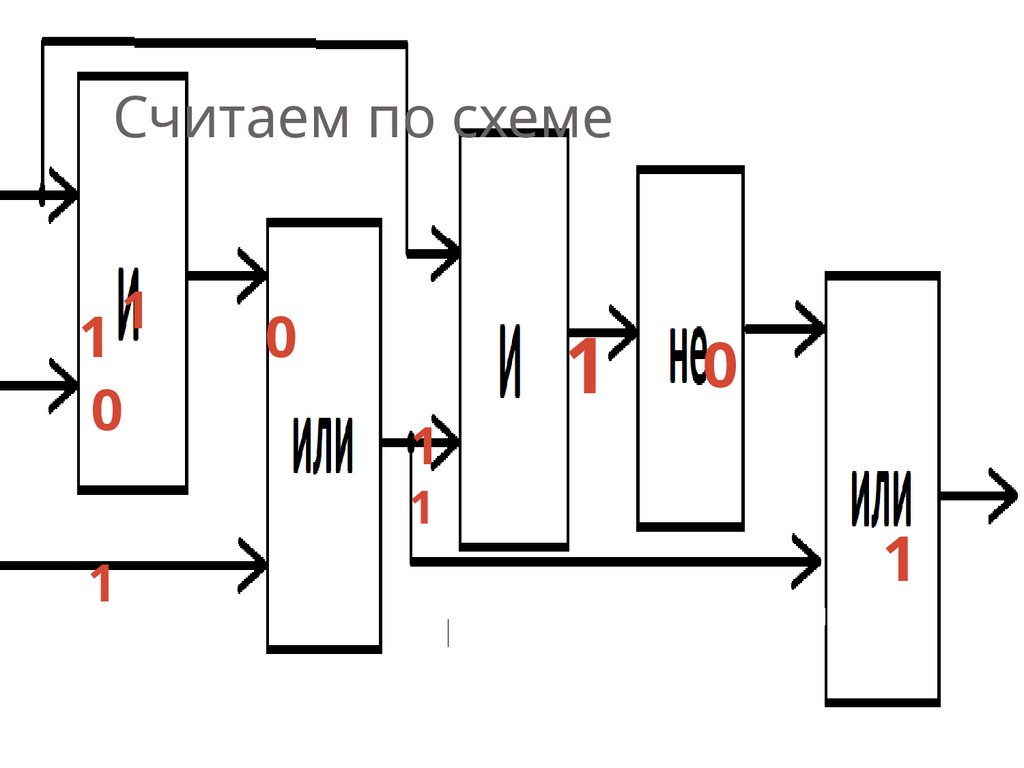
12. Считаем по схеме
11
0
0
1
1
1
1
0
1

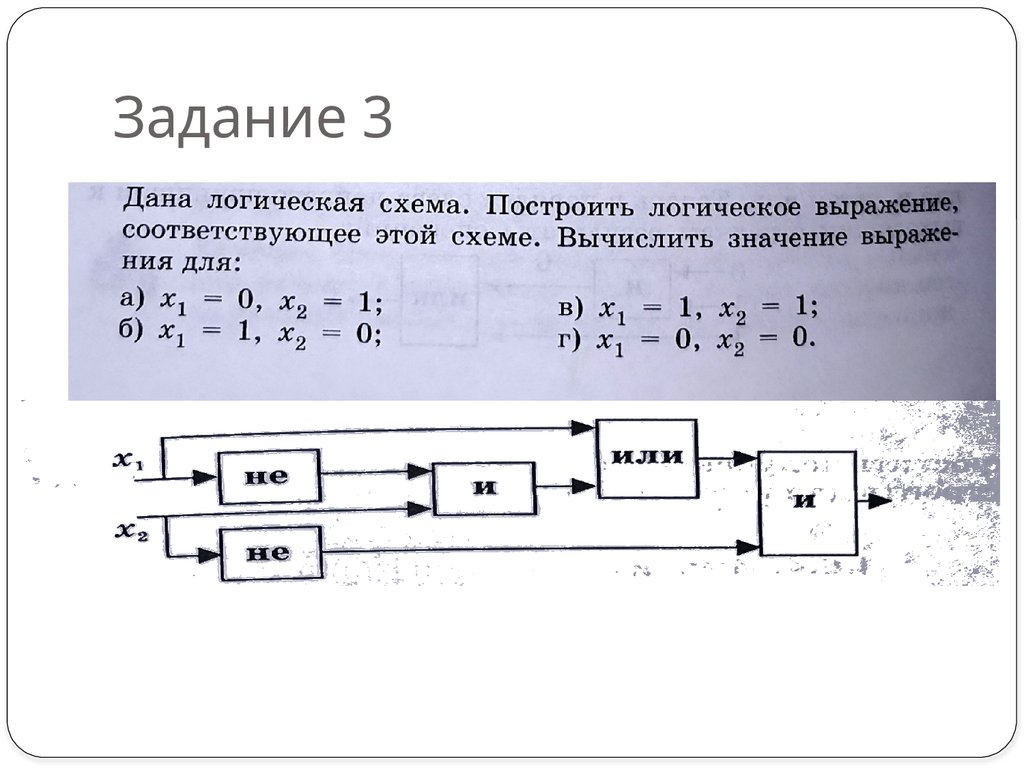
 Информатика
Информатика








