урок№1-4(призн.парал.пр.) — ждя эльжура

1.

Глава III Параллельные прямые.
Стр. 66
Признаки параллельности двух
прямых.

2.

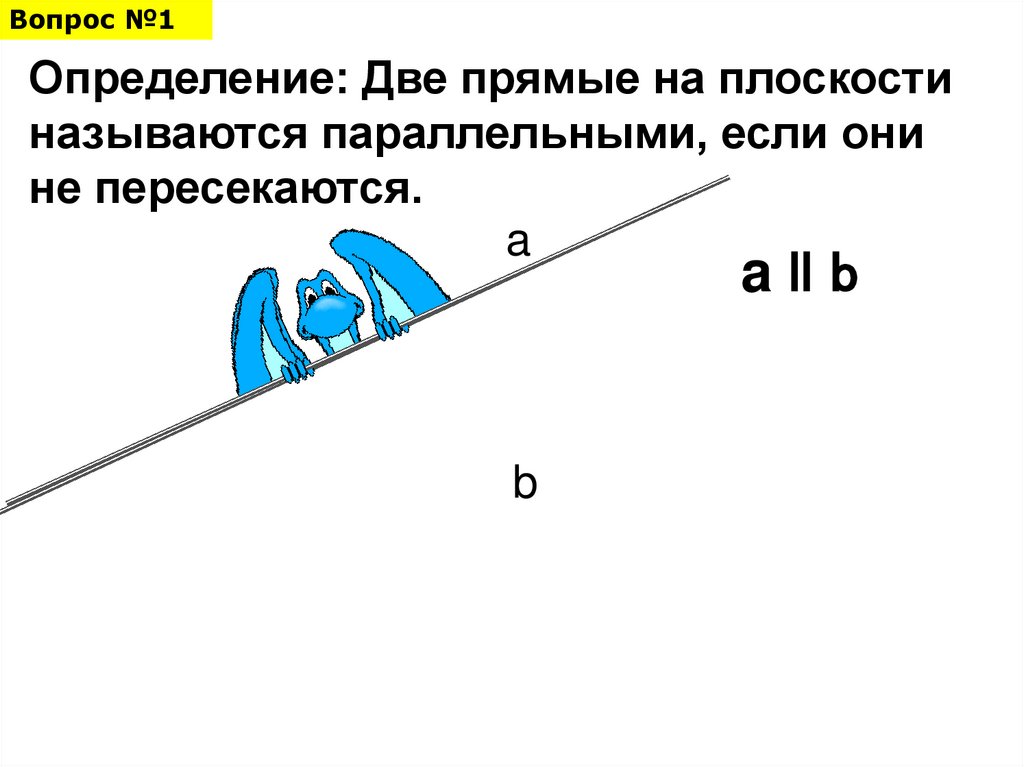
Вопрос №1
Определение: Две прямые на плоскости
называются параллельными, если они
не пересекаются.
a
a ll b
b

3.

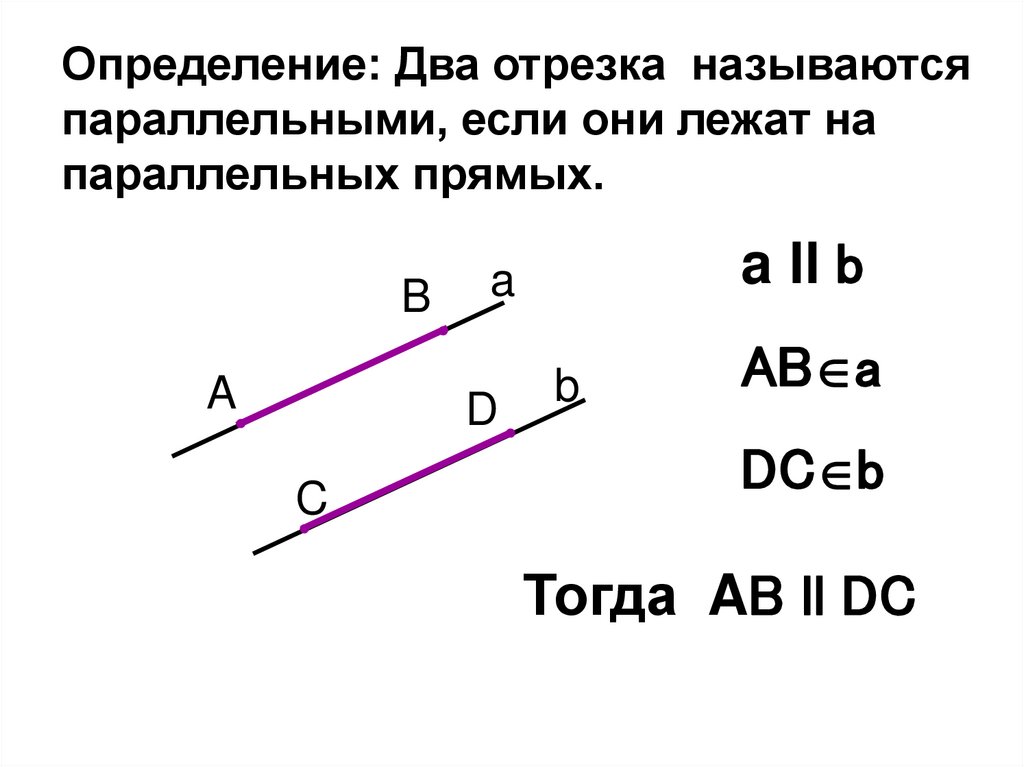
Определение: Два отрезка называются
параллельными, если они лежат на
параллельных прямых.
B
A
D
C
a ll b
a
b
AB a
DC b
Тогда AB ll DC

4.

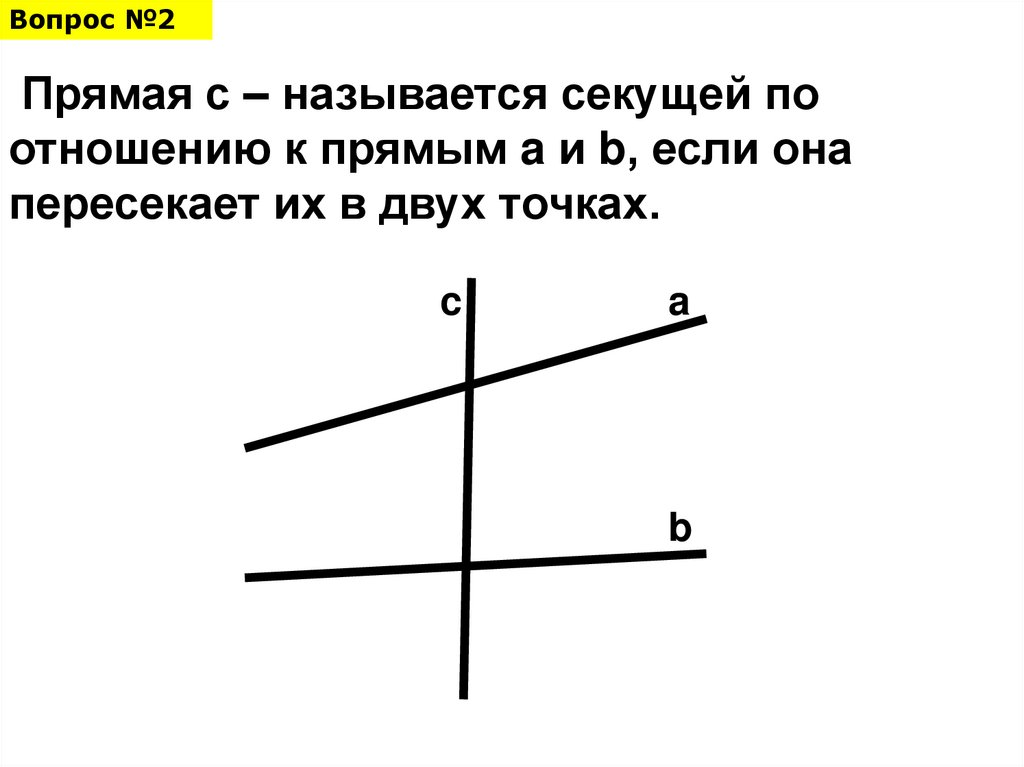
Вопрос №2
Прямая с – называется секущей по
отношению к прямым a и b, если она
пересекает их в двух точках.
c
a
b

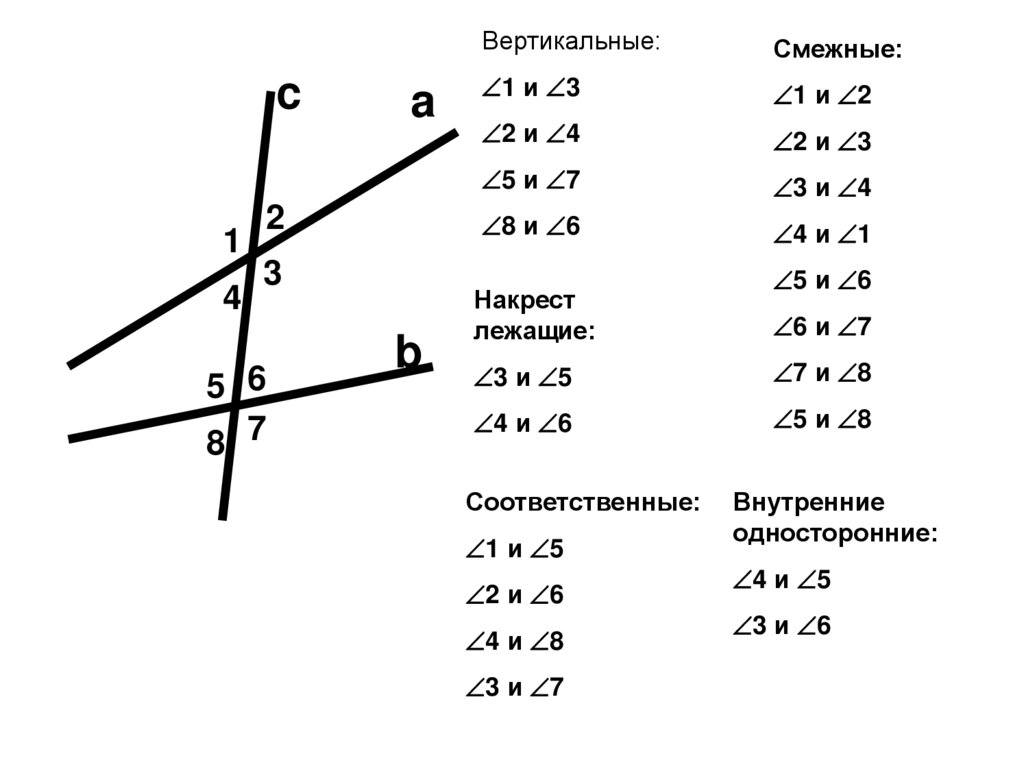
5.

c
1
4
a
2
3
5 6
8 7
b
Вертикальные:
Смежные:
1 и 3
1 и 2
2 и 4
2 и 3
5 и 7
3 и 4
8 и 6
4 и 1
Накрест
лежащие:
5 и 6
6 и 7
3 и 5
7 и 8
4 и 6
5 и 8
Соответственные:
1 и 5
2 и 6
4 и 8
3 и 7
Внутренние
односторонние:
4 и 5
3 и 6

6.

Вопрос №3
Теорема:(первый признак параллельности двух прямых)
Если при пересечении двух прямых секущей накрест
лежащие углы равны, то прямые параллельны.
Дано: a, b – прямые
1 случай: 1= 2 = 90
c
c – секущая
1= 2 – накрест
лежащие
Доказать: a ll b
a
1
2
b

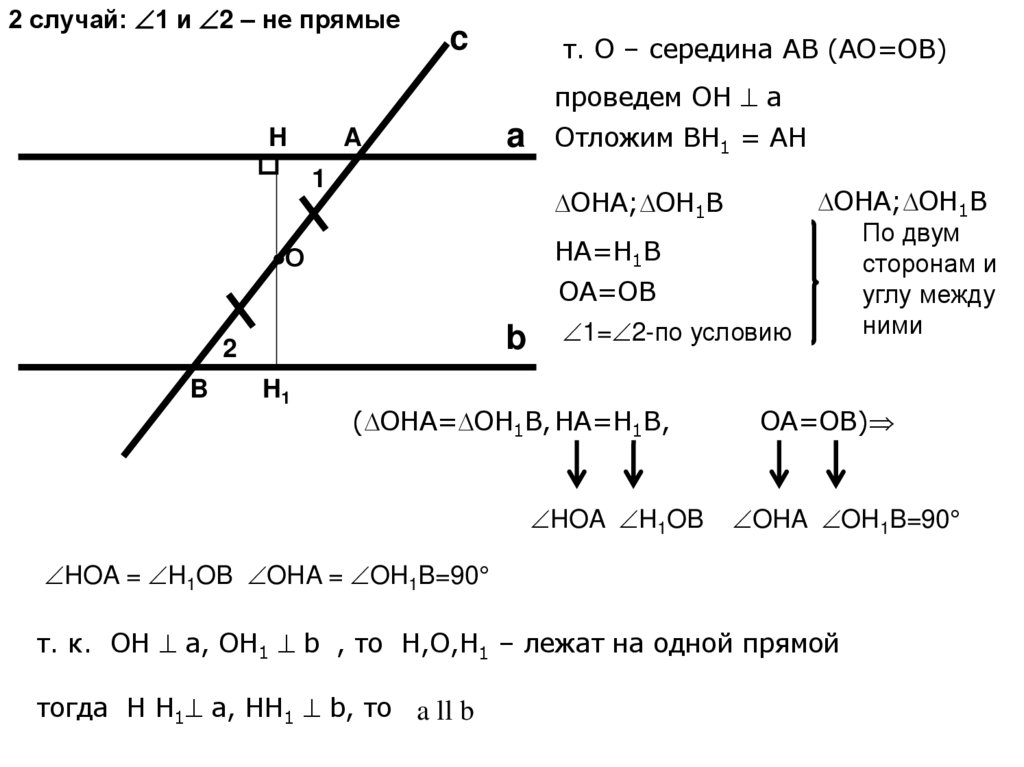
7.

2 случай: 1 и 2 – не прямые
c
т. О – середина AB (AO=OB)
проведем OH a
H
A
a
1
Отложим BH1 = AH
OHA; OH1B
HA=H1B
О
OA=OB
b
2
B
H1
1= 2-по условию
( OHA= OH1B, HA=H1B,
HOA H1OB
OHA; OH1B
По двум
сторонам и
углу между
ними
OA=OB)
OHA OH1B=90
HOA = H1OB OHA = OH1B=90
т. к. OH a, OH1 b , то H,O,H1 – лежат на одной прямой
тогда H H1 a, HH1 b, то a ll b

8.

Вопрос №4
Теорема:(второй признак параллельности двух прямых)
Если при пересечении двух прямых секущей
соответственные углы равны, то прямые параллельны.
Дано: a, b – прямые
c – секущая
1= 2 –
соответственные
Доказать: a ll b
2= 3-вертикальные
2= 1-по условию
2
3 4
b
1
a
c
,тогда 3= 1-накрест лежащие
При a и b, секущей с
,тогда a b (по 1 признаку прямых)

9.

Вопрос №5
Теорема:(третий признак параллельности двух прямых)
Если при пересечении двух прямых секущей сумма
односторонних углов равна 180 , то прямые
параллельны.
Дано: a, b – прямые
c – секущая
1+ 4 =180 односторонние
Доказать: a ll b
2
3 4
b
1
a
c
3+ 4=180 -смежные
3=180 - 4
1+ 4=180 -по условию
1=180 - 4
,тогда 3= 1-накрест лежащие, при a и b, секущей с
,тогда a b (по 1 признаку прямых)

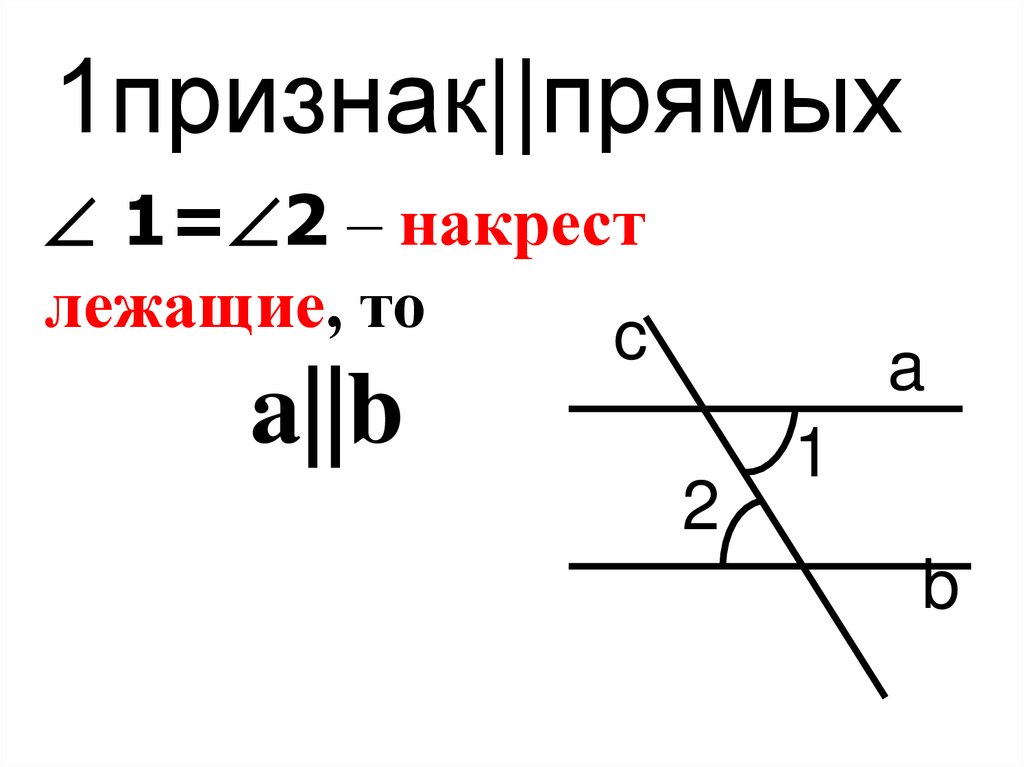
10.

1признак||прямых
1= 2 – накрест
лежащие, то
c
a
a||b
2
1
b

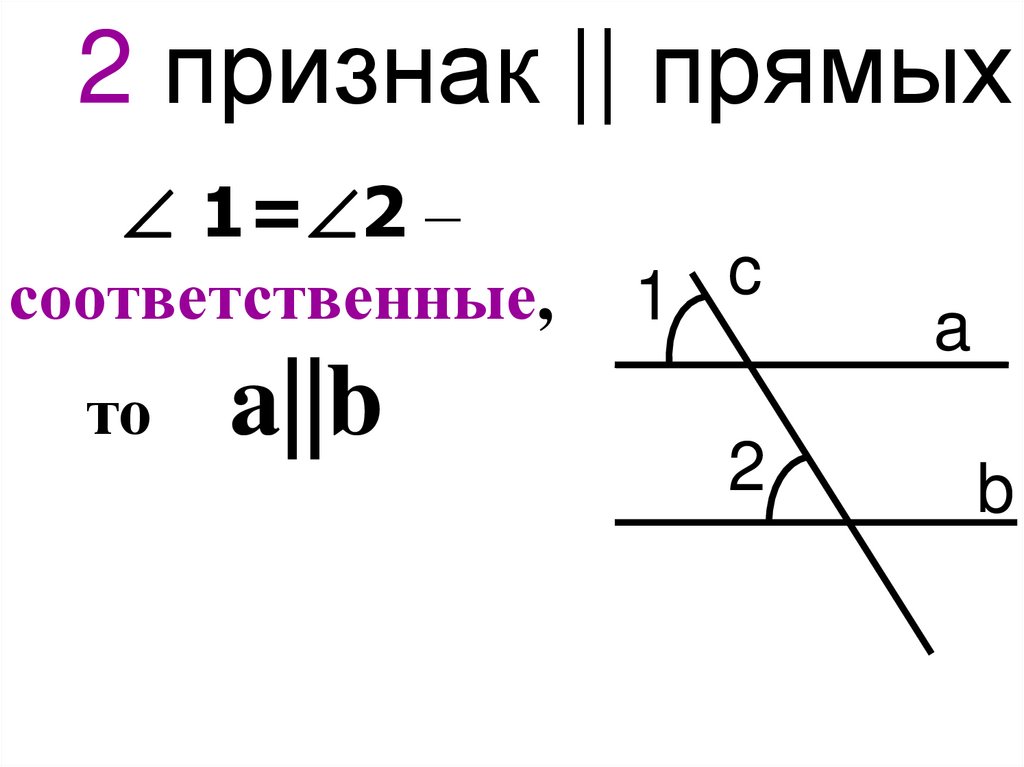
11.

2 признак || прямых
1= 2 –
соответственные,
то
a||b
c
1
2
a
b

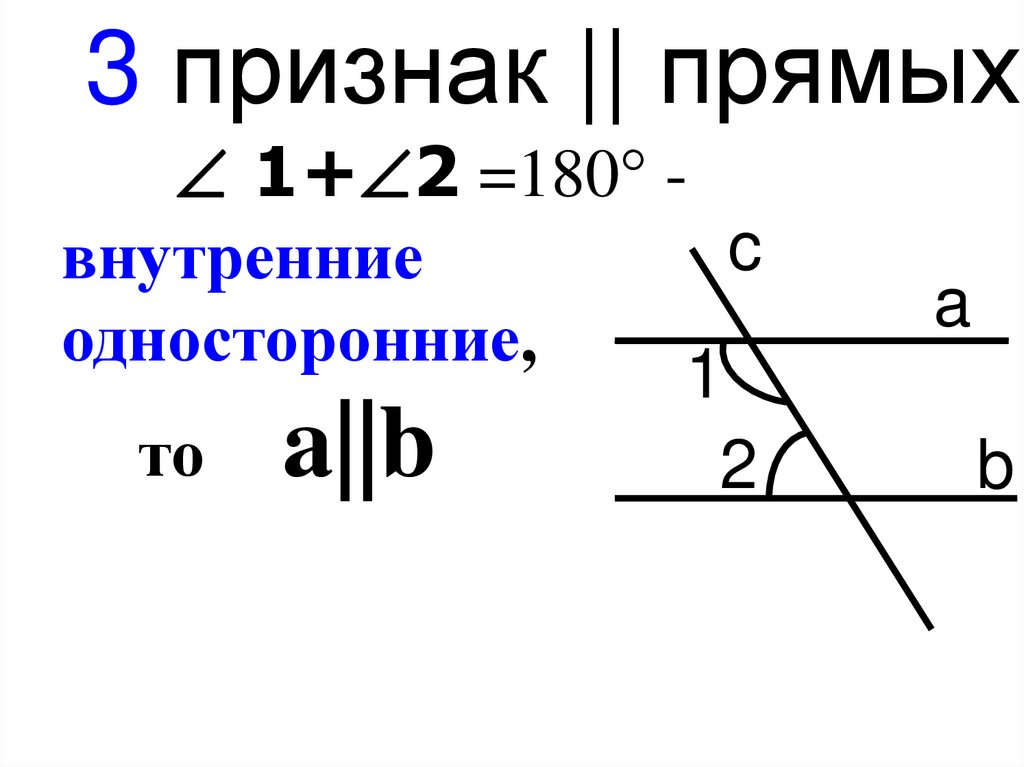
12.

3 признак || прямых
1+ 2 =180° c
внутренние
односторонние,
1
то a||b
2
a
b

13.

Домашнее задание:
Вопрос: 2 1-3- выучить теорию.
№ 186(а).
Желаю
успехов!