Геометрия дорог

1.

Геометрия дорог
Часть 1
Выполнила студентка 4 курса
Михайлова Оксана

2.

План вебинара
Сформулируем, что такое параллельные прямые
Подумаем, где встречается параллельность прямых
Изучим накрест лежащие, соответственные и односторонние углы
Рассмотрим признаки параллельности прямых

3.

Геометрия дорог

4.

Взаимное расположение двух прямых
Как две прямые, лежащие в одной плоскости, могут располагаться
по отношению друг к другу?
Пересекающиеся прямые
Непересекающиеся прямые
a
b
a
b

5.

Параллельные прямые
Определение:
Две прямые на плоскости
называются
параллельными,
если они не пересекаются.
a
b
a ∥ b

6.

Где встречаются параллельные прямые?

7.

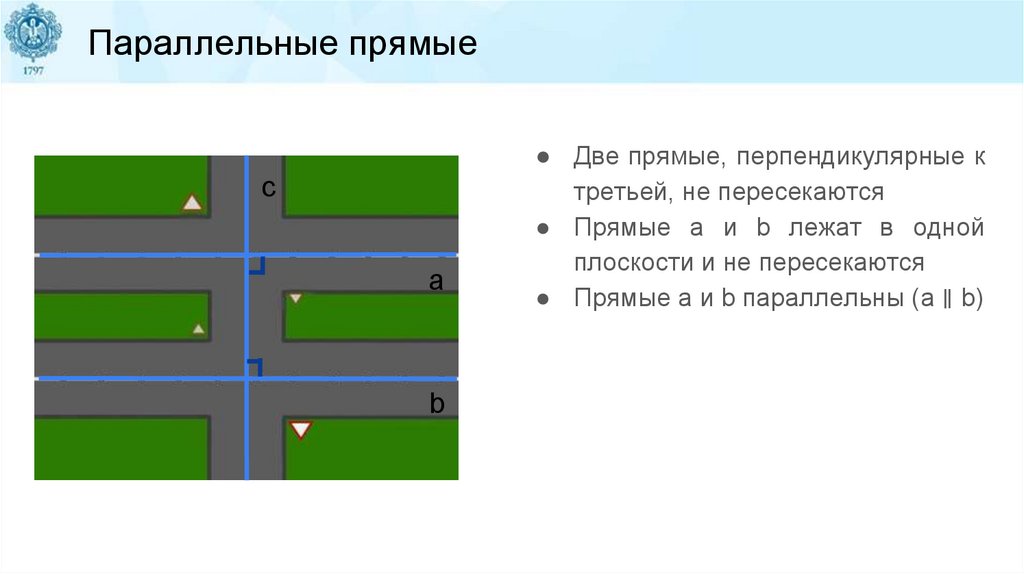
Параллельные прямые
c
a
b
● Две прямые, перпендикулярные к
третьей, не пересекаются
● Прямые a и b лежат в одной
плоскости и не пересекаются
● Прямые a и b параллельны (a ∥ b)

8.

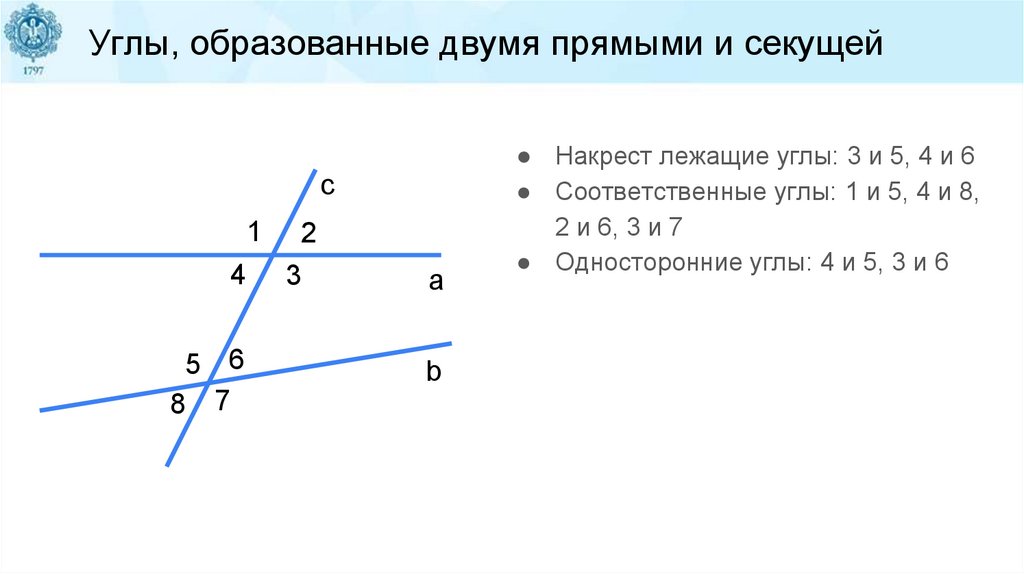
Углы, образованные двумя прямыми и секущей
c
1
4
5 6
8 7
2
3
a
b
● Накрест лежащие углы: 3 и 5, 4 и 6
● Соответственные углы: 1 и 5, 4 и 8,
2 и 6, 3 и 7
● Односторонние углы: 4 и 5, 3 и 6

9.

Как определить, что прямые параллельны?
Признак параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие
углы равны, то прямые параллельны
c
1
a
∠1 = ∠2
2
b

10.

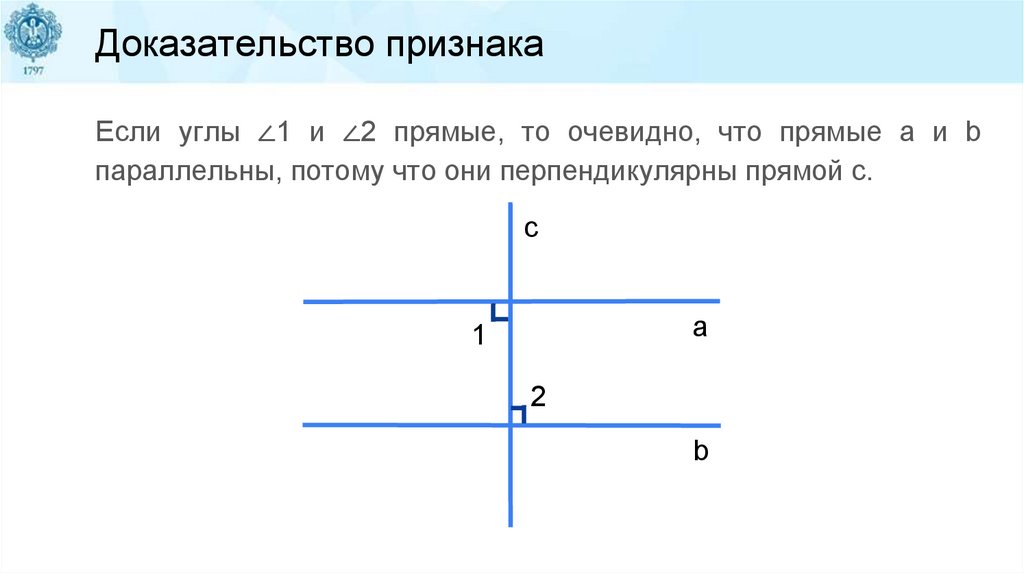
Доказательство признака
Если углы ∠1 и ∠2 прямые, то очевидно, что прямые a и b
параллельны, потому что они перпендикулярны прямой c.
c
a
1
2
b

11.

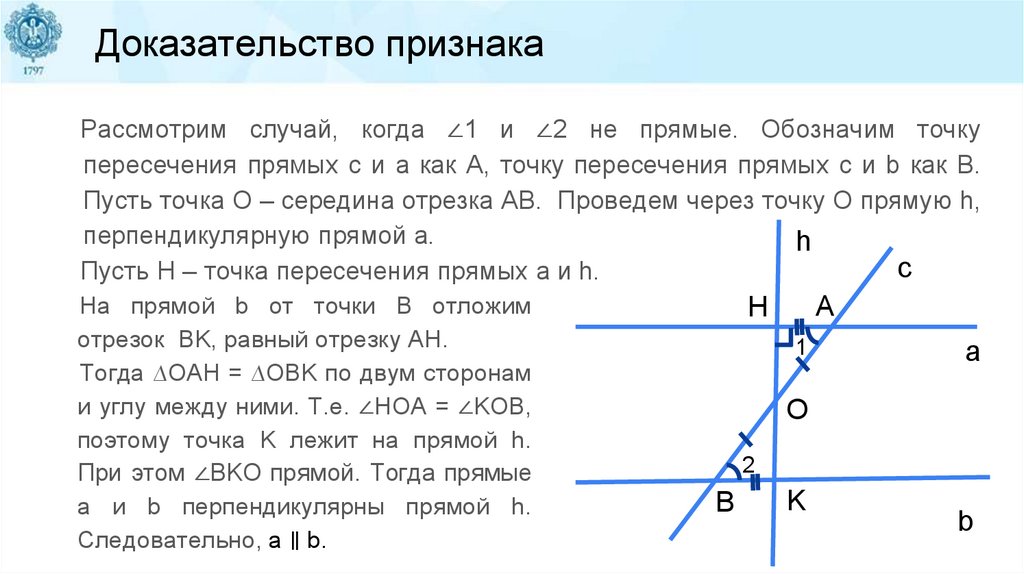
Доказательство признака
Рассмотрим случай, когда ∠1 и ∠2 не прямые. Обозначим точку
пересечения прямых c и a как A, точку пересечения прямых c и b как B.
Пусть точка O – середина отрезка AB. Проведем через точку O прямую h,
перпендикулярную прямой a.
h
c
Пусть H – точка пересечения прямых a и h.
На прямой b от точки B отложим
отрезок BK, равный отрезку AH.
Тогда ∆OAH = ∆OBK по двум сторонам
и углу между ними. Т.е. ∠HOA = ∠KOB,
поэтому точка K лежит на прямой h.
При этом ∠BKO прямой. Тогда прямые
a и b перпендикулярны прямой h.
Следовательно, a ∥ b.
A
H
1
a
O
2
B
K
b

12.

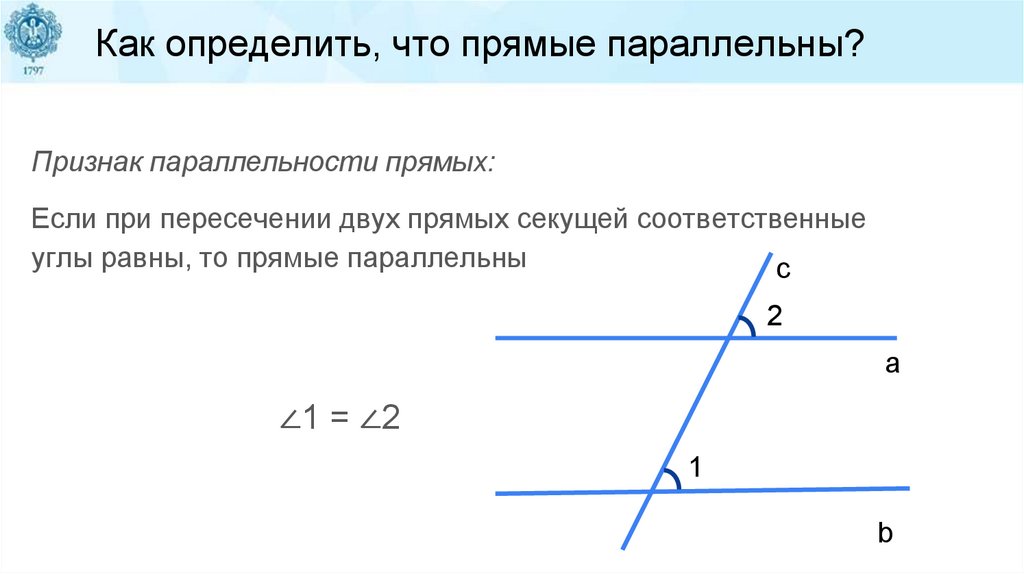
Как определить, что прямые параллельны?
Признак параллельности прямых:
Если при пересечении двух прямых секущей соответственные
углы равны, то прямые параллельны
c
2
a
∠1 = ∠2
1
b

13.

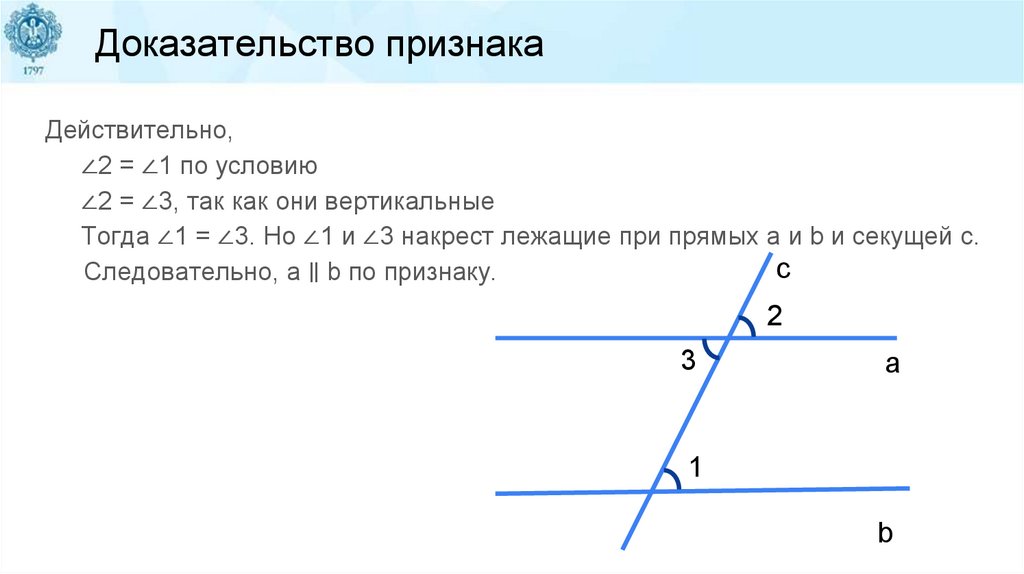
Доказательство признака
Действительно,
∠2 = ∠1 по условию
∠2 = ∠3, так как они вертикальные
Тогда ∠1 = ∠3. Но ∠1 и ∠3 накрест лежащие при прямых a и b и секущей c.
c
Следовательно, a ∥ b по признаку.
2
3
a
1
b

14.

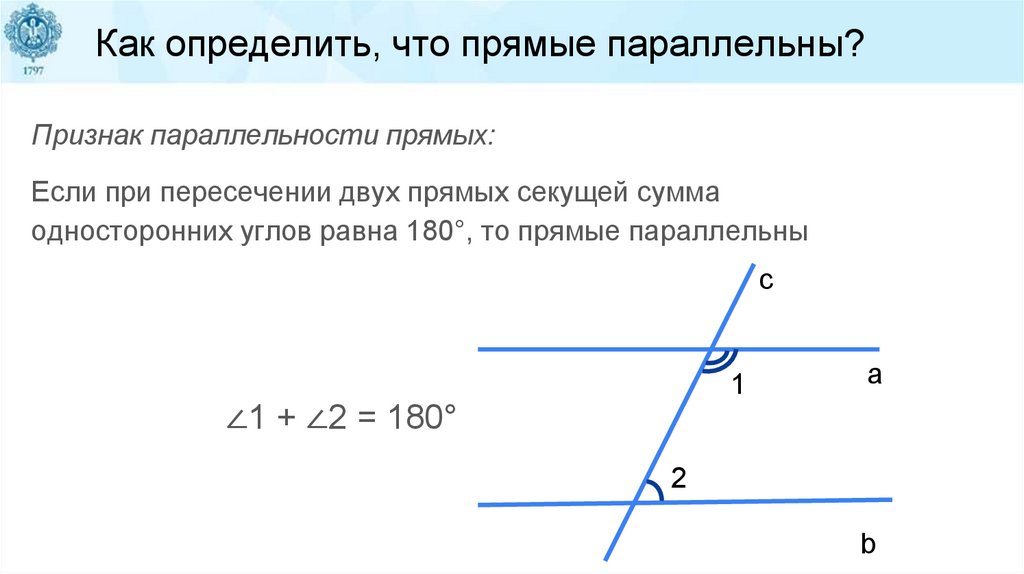
Как определить, что прямые параллельны?
Признак параллельности прямых:
Если при пересечении двух прямых секущей сумма
односторонних углов равна 180°, то прямые параллельны
c
1
a
∠1 + ∠2 = 180°
2
b

15.

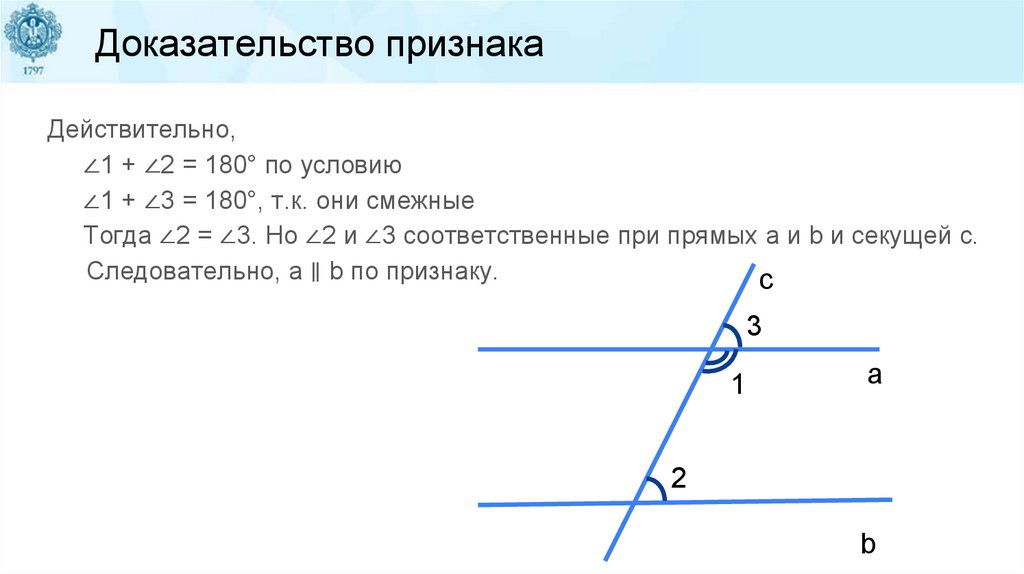
Доказательство признака
Действительно,
∠1 + ∠2 = 180° по условию
∠1 + ∠3 = 180°, т.к. они смежные
Тогда ∠2 = ∠3. Но ∠2 и ∠3 соответственные при прямых a и b и секущей c.
Следовательно, a ∥ b по признаку.
c
3
1
a
2
b

16.

Признаки параллельности двух прямых
● Если при пересечении двух прямых секущей накрест лежащие
углы равны, то прямые параллельны.
● Если при пересечении двух прямых секущей соответственные
углы равны, то прямые параллельны.
● Если при пересечении двух прямых секущей сумма
односторонних углов равна 180°, то прямые параллельны.

17.

Итоги вебинара
На вебинаре мы:
● Познакомились с определением параллельных прямых
● Познакомились с понятием накрест лежащих, соответственных и
односторонних углов
● Рассмотрели и доказали признаки параллельности прямых

18.

Спасибо за внимание!