13 Пути на графах

1. Алгоритмы и структуры данных

Пути на графах
1

2. Эйлеровы циклы и пути

Эйлеров цикл в неориентированном графе:
• начинается в произвольной вершине a
• проходит по всем ребрам графа по одному разу
• завершается в вершине a.
Условия существования эйлерова цикла:
• граф является связным
• степени всех вершин графа (число инцидентных ребер)
четные (т.е. если существует ребро, по которому можно
прийти в вершину, то всегда найдется ребро, по которому
можно выйти).
Если в графе существуют ровно 2 вершины a и b с
нечетными степенями, то можно найти эйлеров путь,
который начинается в a, проходит по всем ребрам по
одному разу и заканчивается в b.
2

3. Идея алгоритма построения цикла/пути

1. Вычисляются степени всех вершин. Если условия
существования цикла/пути не выполняются, то выход.
2. Выбирается произвольная вершина a (для цикла) или
выделяются 2 вершины с нечетными степенями a и b
(для пути).
3. Строится произвольный начальный (далее текущий) цикл
из a или путь из a в b.
4. Для всех вершин v текущего цикла/пути (начиная с v=a)
проверяется, есть ли еще не пройденные ребра,
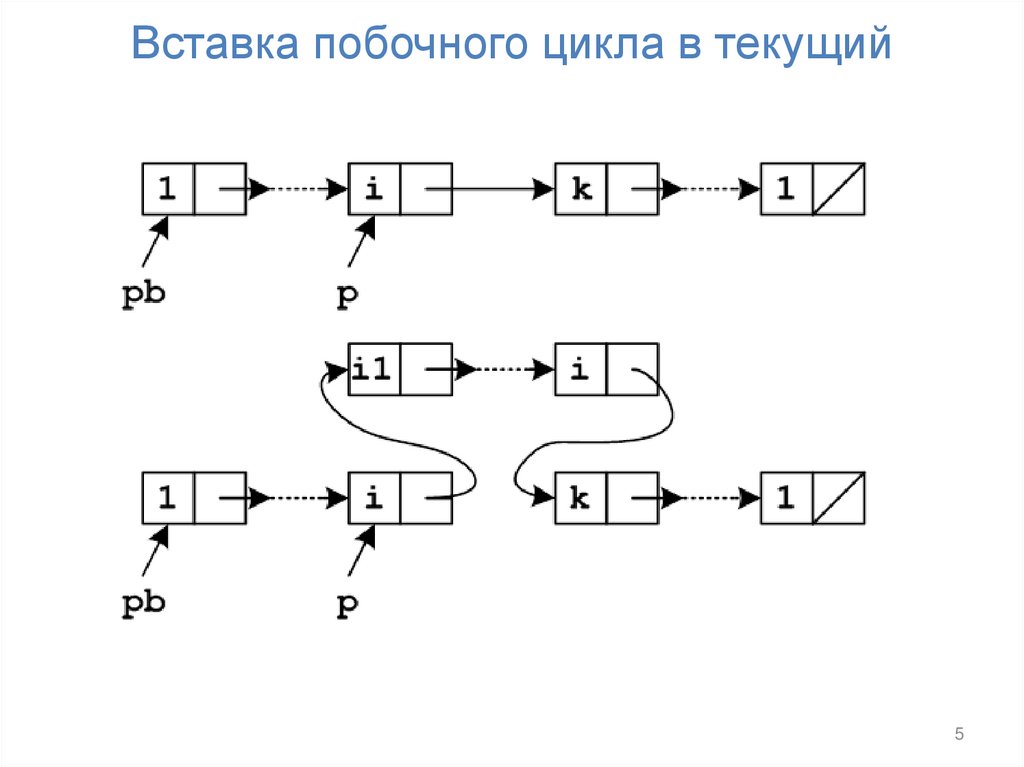
инцидентные v. Если есть, то выделяется побочный
цикл, который начинается и заканчивается в v и проходит
по не проверенным ранее ребрам. Далее побочный цикл
включается в текущий непосредственно за вершиной v.
3

4. Замечания по алгоритму

Текущий путь и побочные циклы выгодно строить в виде
списков. Элементы списков будут хранить номера вершин.
Наиболее удобным представлением графа будет массив
списков смежных вершин: в качестве следующей вершины
пути можно выбирать начальный элемент списка
предыдущей вершины, а затем исключать пройденное
ребро, удаляя нужные элементы в списках этих вершин.
Функциональности класса IList из раздела «Линейные
списки» здесь недостаточно. Необходимо, чтобы класс
включал методы, позволяющие включать новый список за
текущей позицией исходного и удалять элемент с
заданным значением.
4

5. Вставка побочного цикла в текущий

5

6. Гамильтоновы циклы и пути

Гамильтонов цикл в неориентированном графе:
• начинается в произвольной вершине a
• проходит по ребрам через все вершины графа по одному
разу
• завершается в вершине a.
Если в графе найдутся такие 2 вершины a и b, что переходя
из a по ребрам можно попасть в b, обойдя все остальные
вершины по одному разу, то в графе существует
гамильтонов путь (гамильтонова цепь) из a в b.
Очевидно, что гамильтонов цикл/путь не может проходить по
одному и тому же ребру дважды.
Гамильтонов
цикл/путь
в
ориентированном
графе
определяется аналогично (ребра заменяются на дуги).
6

7. Гамильтоновы циклы и пути

Для
графов
нет
явных
аналитических
условий
существования
гамильтонова
цикла/пути,
поэтому
решение можно найти только путем перебора вариантов
путей.
Любой
гамильтонов
цикл/путь
задается
некоторой
перестановкой номеров вершин графа. Получать все
перестановки, а затем проверять, соответствуют ли они
некоторому пути в графе, невыгодно.
Необходимо как можно раньше отсекать варианты, которые
не соответствуют путям в графе, когда переход из
предыдущей вершины в следующую невозможен.
7

8. Гамильтоновы циклы и пути

Рекурсивная функция ham_loops , которая выделяет все
гамильтоновы циклы в графе с n вершинами
представляет
собой
модифицированный
алгоритм
генерации всех перестановок из n элементов.
Параметры функции:
M – матрица смежности графа,
n – число вершин,
k – текущая позиция в пути (определяет глубину рекурсии),
Path – массив, в котором будут сохраняться пути,
Inc – массив отметок пройденных вершин.
8

9. Алгоритм поиска всех гамильтоновых циклов

void ham_loops(bool **M, int n, int k,
int *Path, bool *Inc)
{ int i, j;
for (i = 0; i < n; i++)
if (!Inc[i] && M[Path[k-1]][i])
{
Path[k] = i; Inc[i] = true;
if (k == n-1)
{ if (M[i][0]) PROCESS_LOOP(Path, n); }
else ham_loops(M, n, k+1, Path, Inc);
Inc[i] = false;
}
}
9

10. Обертка для рекурсивной функции

Для функции ham_loops необходимо заранее выделить 2
массива и задать начальную вершину пути. Используем
для этого функцию-обертку:
void hamilton_loops(bool **M, int n)
{
int *Path = new int[n];
bool *Inc = new bool[n];
for (int i = 1; i < n; i++) Inc[i] = false;
Path[0] = 0; Inc[0] = true;
ham_loops(M, n, 1, Path, Inc);
delete [] Inc;
delete [] Path;
}
Трудоемкость: