Pravilnye-i-polupravilnye-mnogogranniki

1.

Правильные и
полуправильные
многогранники
Проектная работа ученика 10 класса
Погрузимся в удивительный мир геометрических форм, изучим их
свойства и применение.

2.

ГЕОМЕТРИЯ
ОСНОВЫ
Что такое многогранник?
Многогранник — это трехмерная геометрическая фигура,
ограниченная плоскими многоугольниками, называемыми
гранями. Это фундаментальное понятие в стереометрии,
которое помогает описывать различные объекты в
окружающем мире.
Гранями многогранника являются многоугольники.
Ребра — это отрезки, по которым соединяются грани.
Вершины — это точки, в которых сходятся ребра.
Примеры многогранников включают призмы, пирамиды, параллелепипеды и, конечно же, правильные и полуправильные
многогранники.

3.

КЛАССИФИКАЦИЯ
ПЛАТОНОВЫ ТЕЛА
Правильные многогранники — определение и
классификация
Правильный многогранник (или платоново тело) — это выпуклый многогранник, обладающий уникальными свойствами
симметрии. Все его грани являются одинаковыми правильными многоугольниками, и в каждой вершине сходится одинаковое
число граней.
Тетраэдр
Куб (Гексаэдр)
Октаэдр
4 грани — правильные треугольники.
6 граней — квадраты.
8 граней — правильные
треугольники.
Додекаэдр
Икосаэдр
12 граней — правильные пятиугольники.
20 граней — правильные треугольники.
Существует всего 5 таких многогранников, что делает их особенно интересными для изучения.

4.

АРХИМЕДОВЫ ТЕЛА
СЛОЖНЫЕ ФОРМЫ
Полуправильные многогранники (тела Архимеда)
В отличие от правильных, полуправильные многогранники имеют
грани, состоящие из правильных многоугольников разных типов.
Однако ключевое свойство симметрии сохраняется: расположение
граней вокруг каждой вершины остается одинаковым.
Их существует 13 видов.
Примеры: кубооктаэдр, усеченный тетраэдр, ромбокубооктаэдр.
Они представляют собой интересное промежуточное звено
между правильными и более сложными многогранниками.
Тела Архимеда менее симметричны, чем платоновы тела, но
обладают сложной и красивой структурой.
Пример: Усеченный октаэдр.

5.

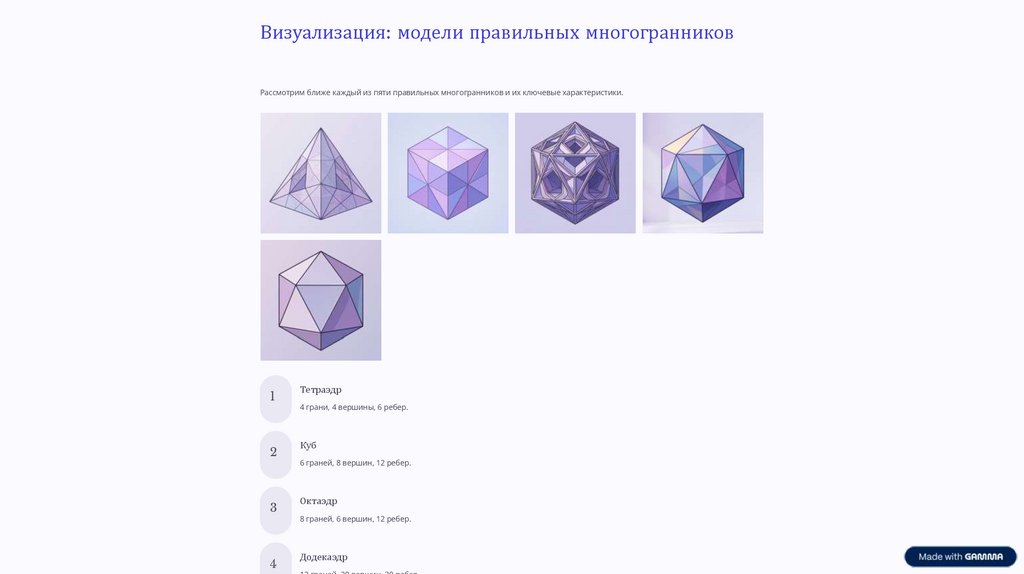
Визуализация: модели правильных многогранников
Рассмотрим ближе каждый из пяти правильных многогранников и их ключевые характеристики.
1
2
3
4
Тетраэдр
4 грани, 4 вершины, 6 ребер.
Куб
6 граней, 8 вершин, 12 ребер.
Октаэдр
8 граней, 6 вершин, 12 ребер.
Додекаэдр

6.

ПРИМЕНЕНИЕ
В РЕАЛЬНОМ МИРЕ
Применение правильных и полуправильных
многогранников
Эти удивительные геометрические формы находят свое применение во множестве областей, от науки до искусства.
Архитектура
Кристаллография
Используются для создания уникальных куполов,
Многие природные кристаллы имеют форму
декоративных элементов зданий и необычных
правильных или полуправильных многогранников,
конструкций, вдохновляя современных
что позволяет лучше понять их структуру и свойства.
архитекторов.
Моделирование и дизайн
Образование
В компьютерной графике, дизайне и инженерии они
Используются как наглядные пособия для изучения
служат базовыми элементами для создания сложных
геометрии, развития пространственного мышления
3D-моделей и инновационных форм.
и понимания математических концепций.

7.

ЗАДАЧА 1
Пример задачи 1: Площадь поверхности куба
Дано:
Площадь полной поверхности куба равна 54 см².
Задача:
Найти длину ребра куба.
Решение:
Площадь поверхности куба S = 6a^2.
Подставляем известные значения: 6a^2 = 54.
Делим обе части на 6: a^2 = 9.
Извлекаем квадратный корень: a = \sqrt{9} = 3 см.
Ответ:
Длина ребра куба составляет 3 см.

8.

ЗАДАЧА 2
Пример задачи 2: Объем тетраэдра
Дано:
Правильный тетраэдр с длиной ребра a = 4 см.
Задача:
Найти объем тетраэдра.
Формула объема правильного тетраэдра:
Вычисление:
Подставляем значение a = 4 в формулу.
V = \frac{4^3 \sqrt{2}}{12} = \frac{64 \sqrt{2}}{12}
V = \frac{16 \sqrt{2}}{3} \approx \frac{16 \times 1.414}{3} \approx \frac{22.624}{3} \approx 7.54 см³.
Ответ:
Объем тетраэдра примерно равен 7.54 см³.

9.

ЗАДАЧА 3
Пример задачи 3: Угол между ребрами октаэдра
Дано:
Правильный октаэдр.
Задача:
Найти угол между двумя ребрами, сходящимися в одной вершине.
Решение:
В правильном октаэдре каждая вершина соединена с четырьмя
другими вершинами, образуя грани, которые являются правильными
треугольниками. Все ребра октаэдра имеют одинаковую длину.
Угол между любыми двумя смежными ребрами, выходящими из
одной вершины октаэдра, всегда одинаков.
Этот угол можно рассчитать, используя свойства правильного
октаэдра или зная, что в каждой вершине октаэдра сходятся 4
правильных треугольника.
Однако, в данном контексте, для угла между ребрами,
сходящимися в одной вершине, речь идет о плоском угле между
гранями или двугранном угле.
Угол между двумя ребрами, сходящимися в одной вершине
правильного октаэдра (например, угол между AC и AD, если A —
вершина, C и D — соседние вершины) равен 90 градусам, если
речь идет о рёбрах, принадлежащих разным граням.
Если вопрос касается двугранного угла между гранями, то этот угол
равен 109° 28' (приблизительно 109.47°).
Объяснение:
Этот угол не является прямым, как можно было бы подумать. Это угол
между плоскостями двух смежных граней октаэдра.
Ответ:
Двугранный угол между гранями октаэдра составляет примерно
109.5^\circ.

10.

Итоги и выводы
1
Уникальность Платоновых тел
Правильных многогранников всего пять — это идеальные, высокосимметричные геометрические фигуры, имеющие глубокое
значение в математике и философии.
2
Разнообразие Архимедовых тел
Полуправильные многогранники расширяют наш класс фигур, демонстрируя богатство и разнообразие форм при сохранении
симметрии.
3
Практическое применение
Задачи с многогранниками помогают не только применить формулы, но и развить логическое и пространственное мышление.
4
Развитие мышления
Изучение многогранников способствует формированию математической культуры и способности анализировать сложные
трехмерные объекты.
Спасибо за внимание!