Похожие презентации:
Тетраэдр, правильный многогранник
1. Тетраэдр - правильный многогранник
Тетраэдр правильныймногогранник
2.
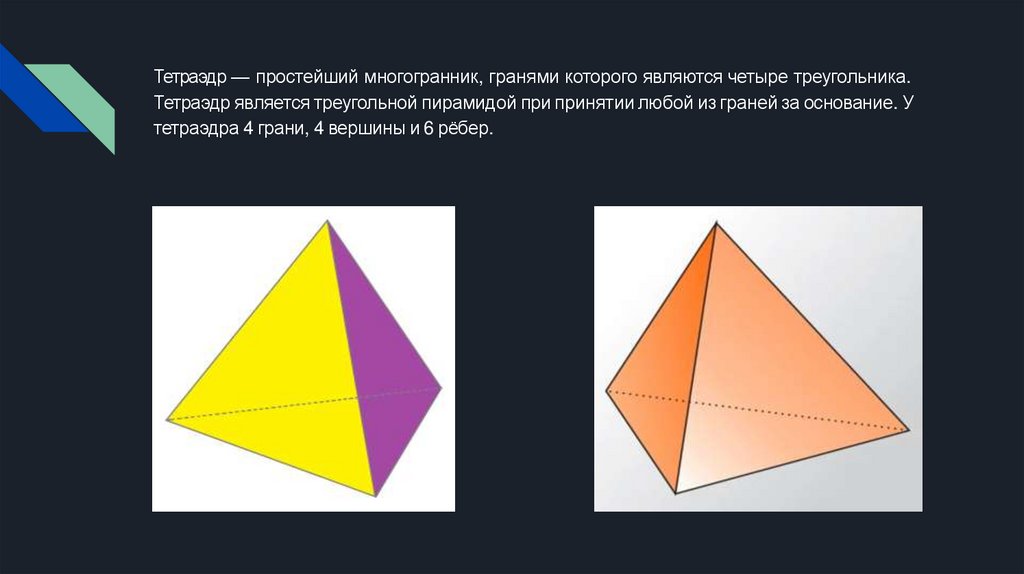
Тетраэдр — простейший многогранник, гранями которого являются четыре треугольника.Тетраэдр является треугольной пирамидой при принятии любой из граней за основание. У
тетраэдра 4 грани, 4 вершины и 6 рёбер.
3.
Платон говорил, что наименьшие частицы огня суть тетраэдры.4.
Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным.Правильный тетраэдр является одним из пяти правильных многогранников. У
правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при
вершинах равны.
5.
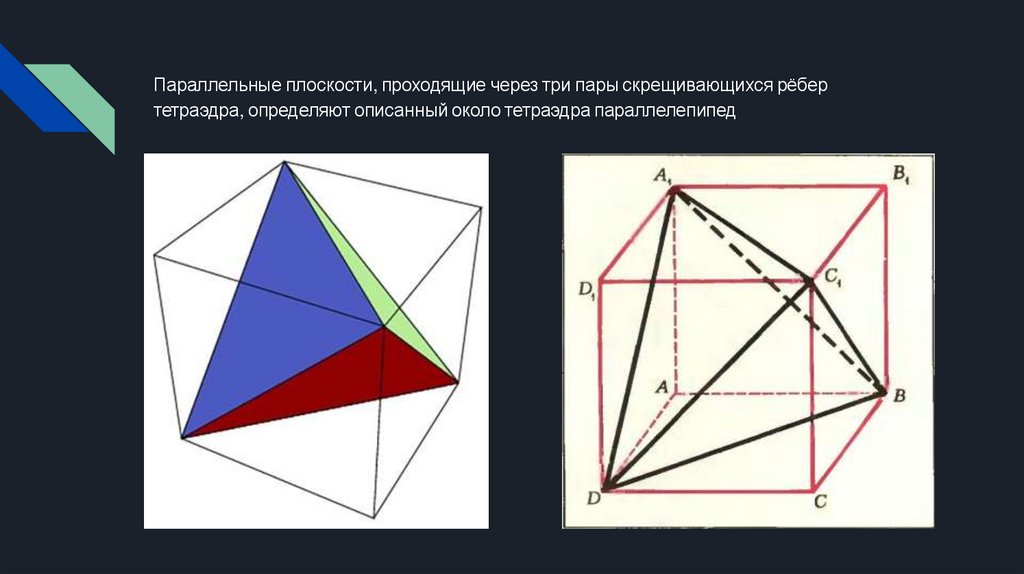
Параллельные плоскости, проходящие через три пары скрещивающихся рёбертетраэдра, определяют описанный около тетраэдра параллелепипед
6.
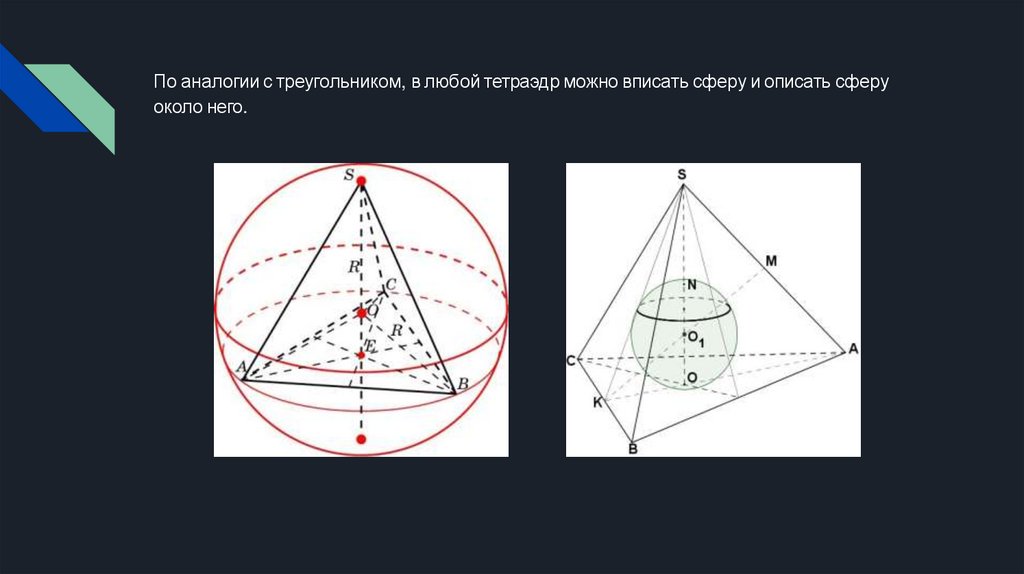
По аналогии с треугольником, в любой тетраэдр можно вписать сферу и описать сферуоколо него.
7.
Правильный тетраэдр имеет три оси симметрии, проходящие через середины трех парскрещивающихся рёбер, и шесть плоскостей симметрии, каждая из которых проходит
через ребро тетраэдра и перпендикулярна тем его гранями, в которых это ребро не лежит.
8.
В правильный тетраэдр можно вписать октаэдр, притом четыре из восьми граней октаэдрабудут совмещены с серединными треугольниками четырёх граней тетраэдра, а все шесть
вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
9. Свойства правильного тетраэдра
Каждая его вершина является вершиной трех равносторонних треугольников. А
значит, сумма плоских углов при каждой вершине будет равна 180°
Объём правильного тетраэдра равен
Площадь поверхности равна
Радиус вписанной сферы равен {\frac {{\sqrt 6}}{12}}a[1]
Радиус описанной сферы равен {\frac {{\sqrt 6}}{4}}a[1]
Радиус полувписанной сферы равен {\displaystyle {\frac {\sqrt {2}}{4}}a}[1]
Высота правильного тетраэдра равна {\displaystyle {\frac {\sqrt {6}}{3}}a} = радиус
вписанной сферы + радиус описанной сферы = {\displaystyle {\frac {\sqrt
{6}}{12}}a+{\frac {\sqrt {6}}{4}}a}
Угол между двумя гранями равен {\displaystyle \arccos {\frac {1}{3}}\approx
70{,}53^{\circ }}
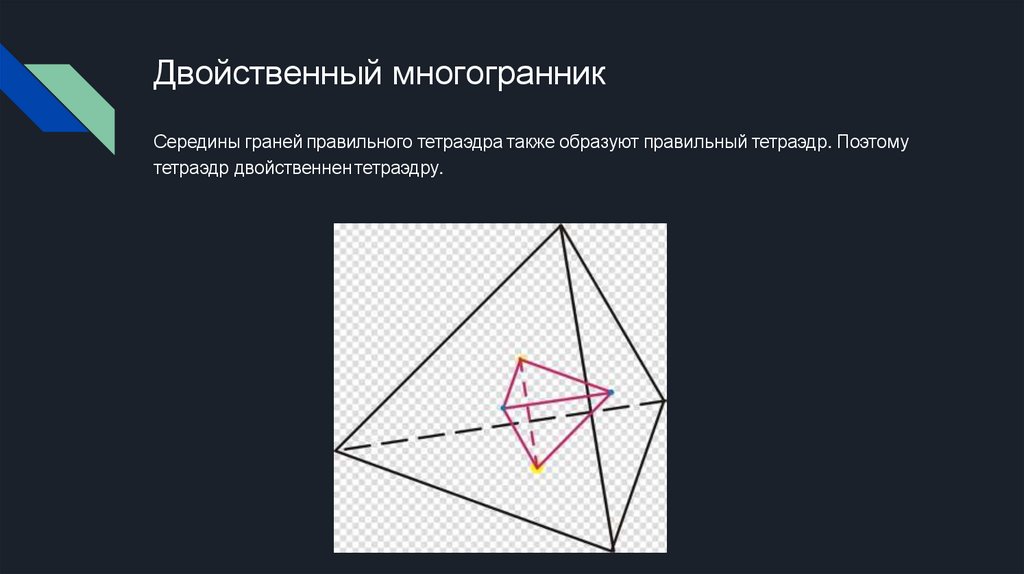
10. Двойственный многогранник
Середины граней правильного тетраэдра также образуют правильный тетраэдр. Поэтомутетраэдр двойственнен тетраэдру.
11.
Тетраэдр является единственным выпуклым многогранников таким, что любые две егограни имеют общее ребро. Единственным из известных невыпуклых многогранников,
удовлетворяющих этому условию является тороидальный многогранник Силаши,
названный по имени венгерского математика, открывшемся его в 1977 г.
12. Тетраэдры в природе
Кристалл сурьмянистогосернокислого натрия
Кристаллическая решетка
алмаза
13.
Молекула метанаИон аммония








 Математика
Математика








