Похожие презентации:
1_4 СЛАУ_Гаусс+24
1.
§ 5. Системы линейных алгебраическихуравнений (СЛАУ)
Опр. 1. Система m уравнений с n неизвестными x1, x2, …, xn
называется системой линейных алгебраических уравнений
(СЛАУ), если она имеет вид
a11 x1 a12 x2
a x a x
21 1 22 2
am1 x1 am 2 x2
a1n xn b1 ,
a2 n xn b2 ,
(1)
amn xn bm ,
где aij, bi (1 ≤ i ≤ m, 1 ≤ j ≤ n) – заданные числа. Число aij –
коэффициент при неизвестной xj в i-м уравнении; bi –
свободный член i-го уравнения.
2.
Опр. 2. Упорядоченный набор чисел (c1, c2, …, cn) называетсярешением системы (1), если каждое из уравнений системы
обращается в верное равенство после подстановки вместо x1, x2,
…, xn соответственно чисел c1, c2, …, cn.
Опр. 3. Система уравнений называется совместной, если она
имеет хотя бы одно решение. Система, не имеющая ни одного
решения, называется несовместной.
Опр. 4. Совместная система уравнений называется
определенной, если она имеет единственное решение, и
неопределенной, если она имеет более одного решения.
3.
Утв. 1. Неопределенная СЛАУ имеет бесконечно многорешений.
Опр. 5. Две системы уравнений называются равносильными
или эквивалентными, если любое решение одной из них
является также решением другой и наоборот.
Опр. 6. СЛАУ, у которой все свободные члены равны нулю,
называется однородной.
Однородная система всегда совместна, так как она всегда
имеет нулевое решение x1 = x2 =…= xn = 0, хотя оно не
обязательно единственно.
4.
Матричная форма записи СЛАУ(2)
AX = B,
a11 a12
a
a22
21
где матрица A
...
...
am1 am 2
... a1n
... a2 n
, составленная из
... ...
... amn
коэффициентов при неизвестных, называется матрицей
системы;
x1
x2
матрица-столбец X – столбцом неизвестных;
...
xn
b1
b
матрица-столбец B 2 – столбцом свободных членов.
...
bm
5.
a11 a12a
a22
21
Матрица A
...
...
am1 am 2
матрицей системы.
... a1n b1
... a2 n b2
называется расширенной
... ... ...
... amn bm
6.
Теорема Кронекера – Капелли7.
Теорема Кронекера – Капелли8.
Теорема Кронекера – КапеллиТh1 [Кронекер, Капелли]. СЛАУ (1), имеющая m
уравнений с n неизвестными, совместна тогда и только тогда,
когда ранг расширенной матрицы системы равен рангу
основной матрицы этой системы, rang A rang A, при этом:
- если ранг матрицы совместной системы равен числу
неизвестных:rang A rang A n, то система имеет единственное
решение;
- если ранг матрицы совместной системы меньше числа
неизвестных rang A rang A n, то система имеет бесконечно
много решений.
В случае, когда ранг матрицы совместной системы меньше числа
неизвестных, вводят понятия базисных (основных) и свободных
(неосновных) переменных.
Базисными
неизвестными
называются
r
неизвестных,
коэффициенты при которых образуют базисный минор; остальные
неизвестные – свободные.
9.
Пример 1. Рассмотрим понятия базисных и свободныхпеременных на примере СЛАУ 5 x1 2 x2 x3 4,
5 x1 2 x2 4 x3 5.
5 2 1 4
5 2 1 4
A
.
II II I
5 2 4 5
0 0 3 1
x1 x2
x3
rang A rang A 2.
В качестве базисного минора преобразованной матрицы можно
взять минор 5 1
0 3
15 0.
Неизвестные x1 и x3 – базисные, а x2 – свободная. Это означает,
что значение переменной x2 может быть выбрано произвольно.
1
4 x3 2 x2 11 2c
5 x1 2 x2 x3 4,
x
,
x
.
Пусть x2 = c.
3
1
3
5
15 5
3x3 1.
11 2c
1
Множество решений системы: ; c; : c R .
3
15 5
10.
Метод ГауссаМетод Гаусса, или метод последовательного исключения
неизвестных, является наиболее универсальным методом решения
СЛАУ. Он применим для решения любых СЛАУ.
На первом этапе (прямой ход) система приводится к
равносильной системе ступенчатого, в частности треугольного
вида, с помощью следующих преобразований:
1) перестановка двух уравнений;
2) умножение уравнения на число, отличное от 0;
3) прибавление к одному уравнению другого, умноженного на число.
При этом сначала исключается переменная x1 из всех
уравнений, кроме первого, затем переменная x2 из всех уравнений,
кроме первого и второго, и т. д.
11.
Алгоритм Гаусса:12.
Аналогичную процедуру применим к оставшимся m-1уравнениям. В результате получим
Продолжая этот процесс и комбинируя с элементарными
операциями над столбцами получим конечную форму
представления
расширенной
матрицы
с
помощью
элементарной операции по алгоритму Гаусса (добавим
элементарную операцию по вычеркиванию нулевых строк и
нулевых столбцов), тогда получим матрицу:
13.
14.
Таким образом, имеем три различные возможности:15.
На первом этапе осуществляется так называемый прямойход, когда путём элементарных преобразований над строками
систему приводят к ступенчатой или треугольной форме,
либо устанавливают, что система несовместна. А именно,
среди элементов первого столбца матрицы выбирают
ненулевой, перемещают его на крайнее верхнее положение
перестановкой строк и вычитают получившуюся после
перестановки первую строку из остальных строк, домножив
её на величину, равную отношению первого элемента каждой
из этих строк к первому элементу первой строки, обнуляя тем
самым столбец под ним. После того, как указанные
преобразования были совершены, первую строку и первый
столбец мысленно вычёркивают и продолжают пока не
останется матрица нулевого размера. Если на какой-то из
итераций среди элементов первого столбца не нашёлся
ненулевой, то переходят к следующему столбцу и
проделывают аналогичную операцию.
16.
На втором этапе (обратный ход) идет последовательноеопределение неизвестных из полученной системы, начиная с
последних по номеру.
Если в полученной системе ступенчатого вида имеется хотя
бы одно уравнение вида 0 x1 0 x2 ... 0 xn b, где b ≠ 0,
то система несовместна.
Пусть в полученной ступенчатой системе таких уравнений
нет, обозначим через r количество уравнений ступенчатой
системы, в которых не все коэффициенты левой части равны
нулю, при этом r ≤ n.
17.
Если r = n, то система имеет единственное решение. В этомслучае из последнего уравнения находим xn, затем, подставляя xn
в предпоследнее уравнение, находим xn–1. Продолжая этот
процесс, найдем единственное решение системы (x1, x2, …, xn).
Если r < n, то из последнего уравнения системы выражаем
одну переменную через остальные n – r переменных (свободных
переменных). Затем подставляем полученное значение в
предпоследнее уравнение и выражаем еще одну переменную
через те же n – r свободных переменных. Продолжая этот
процесс, выразим r неизвестных через свободные переменные.
Придавая свободным переменным произвольные значения,
получим бесчисленное множество решений системы.
18.
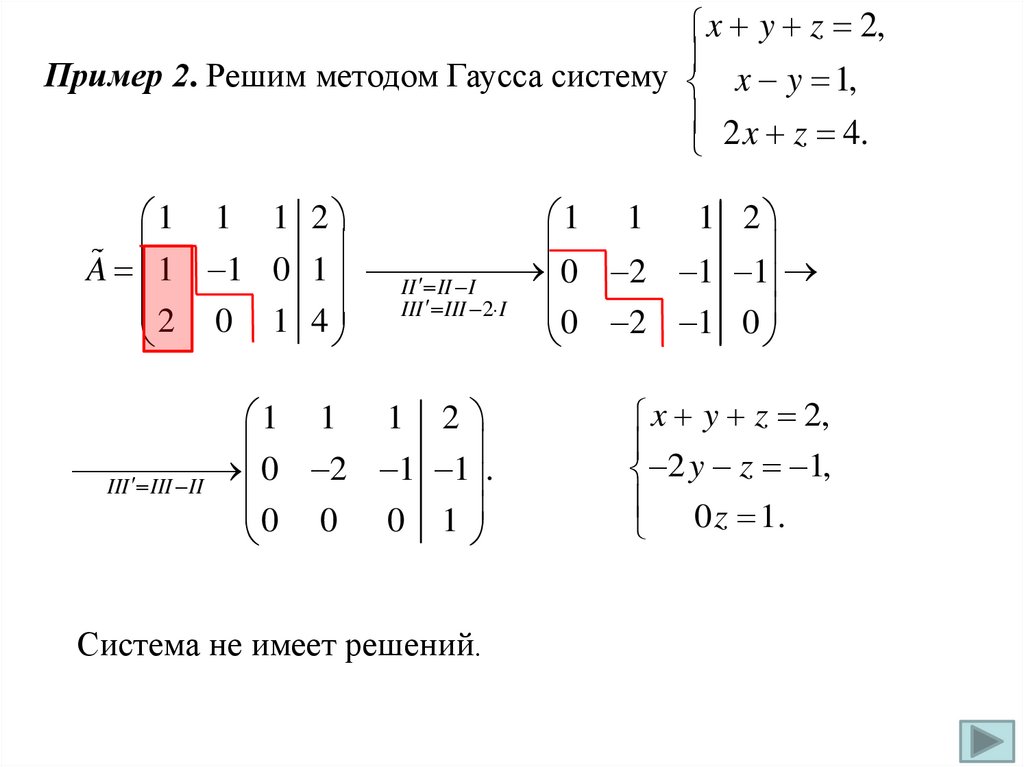
x y z 2,Пример 2. Решим методом Гаусса систему
x y 1,
2 x z 4.
1 1 1 2
1 1
1 2
A 1 1 0 1
0 2 1 1
II II I
III III 2 I
2 0 1 4
0 2 1 0
1 1 1 2
0 2 1 1 .
III III II
0 0 0 1
Система не имеет решений.
x y z 2,
2 y z 1,
0 z 1.
19.
x y z 3,Пример 3. Решим методом Гаусса систему x 2 y z 0,
2 x y 2 z 3.
1 1 1 3
1 1 1 3
A 1 2 1 0 II II I 0 3 0 3
2 1 2 3 III III 2 I 0 3 0 3
1 1 1 3
0 3 0 3 .
III III II
0 0 0 0
x y z 3,
3 y 3,
0 0.
y = 1.
Пусть z = c, где c R ,
x 3 y z 3 1 c 2 c.
Ответ.
(2 с;1; c) : c R .
20.
Пример. Решить систему линейных уравненийx1 2 x2 3 x3 2 x4 6
2 x 4 x 2 x 3 x 18
1
2
3
4
3 x1 2 x2 x3 2 x4 4
2 x1 3 x2 2 x3 x4 8
1 2 3 2 6
2 4 2 3 18
A
3 2 1 2 4
2
3
2
1
8
2
3
2
6
1
2 1 2 4 2 2 2 3 2 3 2 2 18 6 2
3 1 3 2 2 3 1 3 3 2 2 3 4 6 3
2 1 2 3 2 2 2 3 2 1 2 2 8 6 2
21.
3 2 61 2
0 0 8 1
6
0 4 10 8 14
0 7 4 5 20
3 2 6
1 2
0 7 4 5 20
0 4 10 8 14
6
0 0 8 1
2
3
2
6
1
2 1 2 4 2 2 2 3 2 3 2 2 18 6 2
3 1 3 2 2 3 1 3 3 2 2 3 4 6 3
2 1 2 3 2 2 2 3 2 1 2 2 8 6 2
22.
3 2 61 2
0 0 8 1
6
0 4 10 8 14
0 7 4 5 20
3 2 6
1 2
0 7 4 5 20
0 4 10 8 14
6
0 0 8 1
6
1 2 3 2
1 2 3 2 6
0 7 4 5 20
0 1 16 11 8
0 8 20 16 28
0 2 5 4 7
0
0
8
1
6
0 0 8 1 6
2
3
2
6
1
0
1
16
11
8
0 2 1 2 5 16 2 4 11 2 7 8 2
0
8
1
6
0
23.
10
0
0
1
0
0
0
2 3
2 6
1 16 11 8
0 27 18 9
0 8
1
6
2 3 2 6
1 16 11 8
0 1 5 9
0 8 1 6
1
0
0
0
2 3 2
1 16 11
0 9 6
0 8 1
6
8
3
6
2
3
2
6
1
0
1
16
11
8
0 2 1 2 5 16 2 4 11 2 7 8 2
0
8
1
6
0
24.
10
0
0
2 3
2 6
1
0
1 16 11 8
0
0 27 18 9
0 8
1
6
0
2 3 2 6
1 2
0 1
1 16 11 8
0 1 5 9
0 0
0 8 1 6
0 0
1
0
0
0
2 3 2 6
1 16 11 8
0 1 5 9
0 0 39 78
1
0
0
0
1
0
0
0
2 3 2
1 16 11
0 9 6
0 8 1
6
8
3
6
3
2
6
16
11
8
1
5
9
8 8 1 40 6 72
2 3 2 6
1 16 11 8
0 1 5 9
0 0
1 2
25.
10
0
0
2 3 0 2
1 16 0 14
0 1 0 1
0 0 1 2
1
0
0
0
2 3 2 6
1 16 11 8
0 1 5 9
0 0 39 78
1
0
0
0
0 5
0 2
0 1
1 2
2
1
0
0
0
0
1
0
1
0
0
0
2 3 2 6
1 16 11 8
0 1 5 9
0 0
1 2
26.
10
0
0
1
0
0
0
2 3 0 2
1 16 0 14
0 1 0 1
0 0 1 2
0
1
0
0
0
0
1
0
0 1
0 2
0 1
1 2
1
0
0
0
2
1
0
0
0
0
1
0
x1 1
x2 2
x3 1
x4 2
0 5
0 2
0 1
1 2
27.
x1x2
x3
x4
1
0
0
0
2 3 2 6
1 16 11 8
0 1 5 9
0 0
1 2
x4 2
x3 5x4 9 x3 9 5 2 1
x2 16 x3 11x4 8 x2 8 11 2 16 1 2
x1 2 x2 3x3 2 x4 6
x1 2 2 3 1 2 2 6
x1 1



















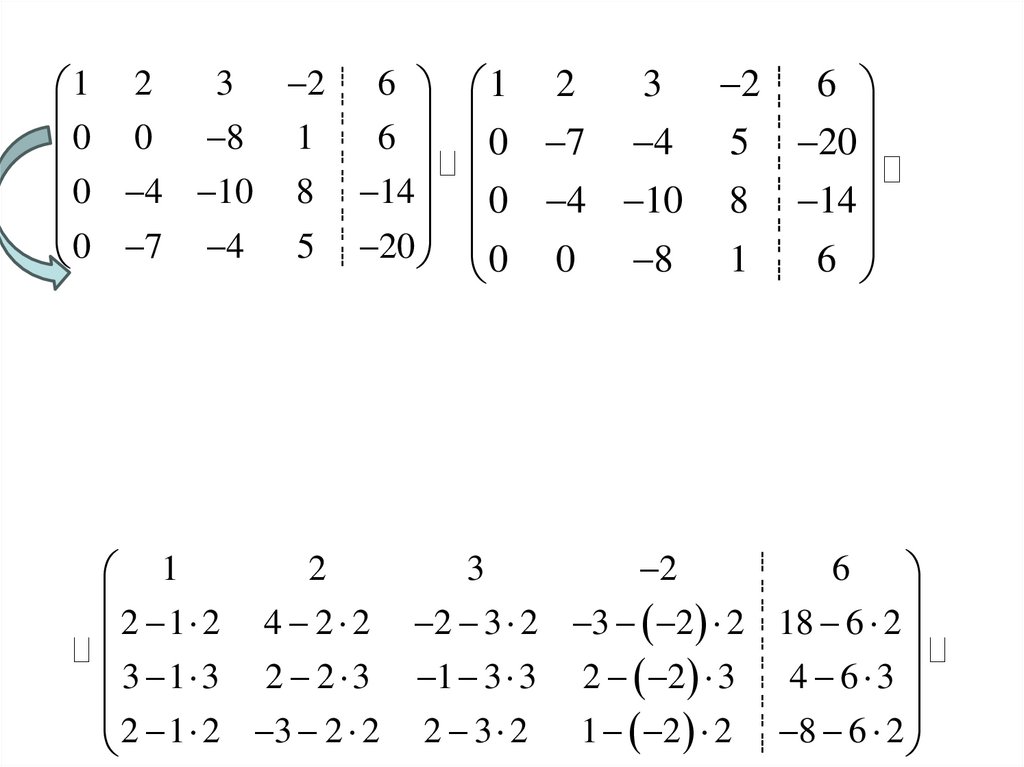





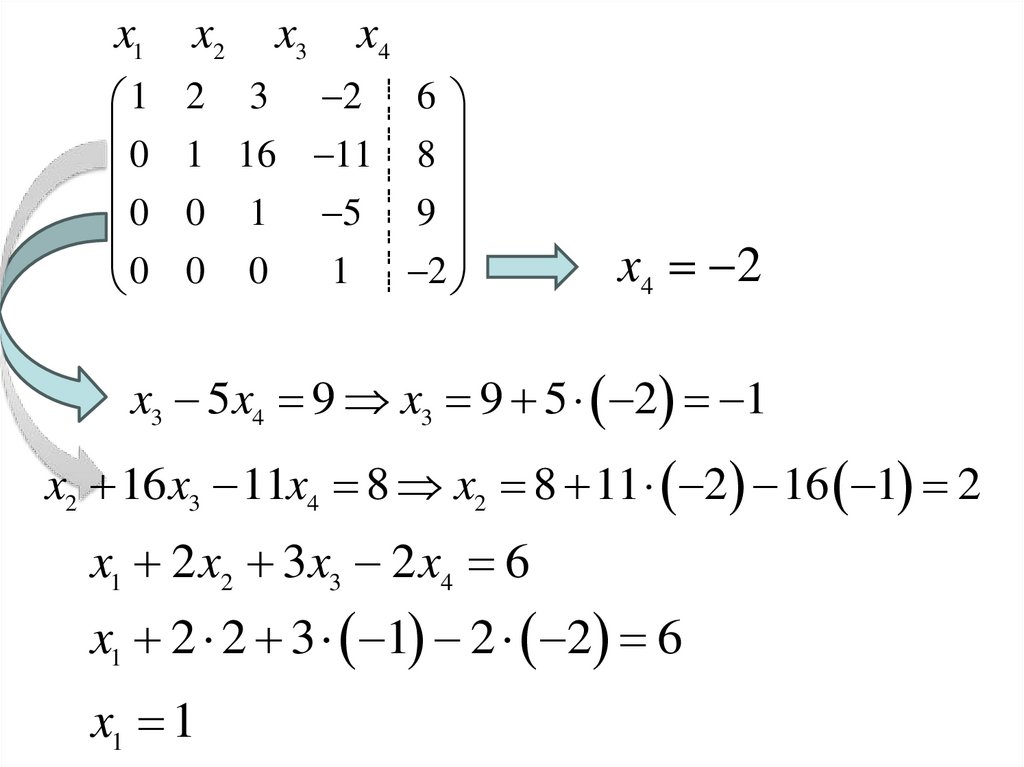
 Математика
Математика








