Похожие презентации:
Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками
1. Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками
1.2.
3.
4.
Предпосылки метода наименьших квадратов
Гетероскедостичность, выявление и устранение
Автокорреляция, выявление и устранение
Мультиколлениарность, выявление и устранение
2. Предпосылки метода наименьших квадратов
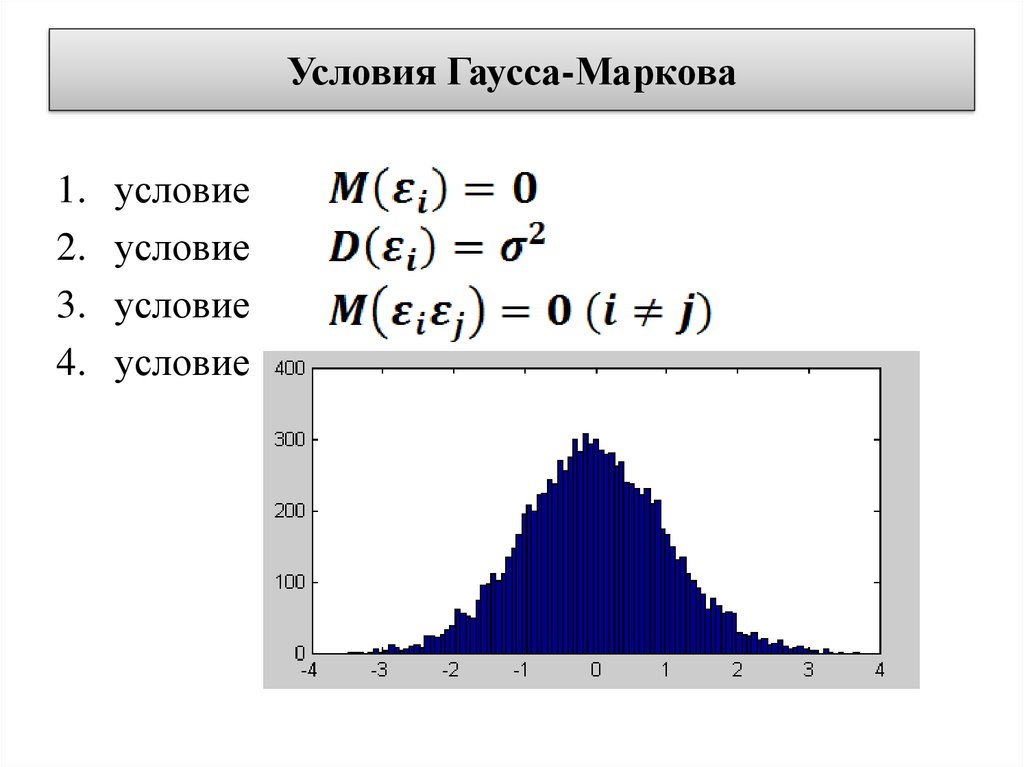
3. Условия Гаусса-Маркова
1.2.
3.
4.
условие
условие
условие
условие
4. Гетероскедостичность, выявление и устранение
5.
СбережениеСбережение
Доход домохозяйства
Доход домохозяйства
гомоскедостичность
гетероскедостичность
гомоскедостичность
гетероскедостичность
6.
Пример гетероскедостичности в пространственныхданных: эффект масштаба
X – стоимость основных производственных фондов
(млн. руб.)
Y – прибыль предприятия (млн. руб.).
7.
120100
80
60
Y
40
20
0
0
10
20
30
40
50
60
X
70
80
90
100
110
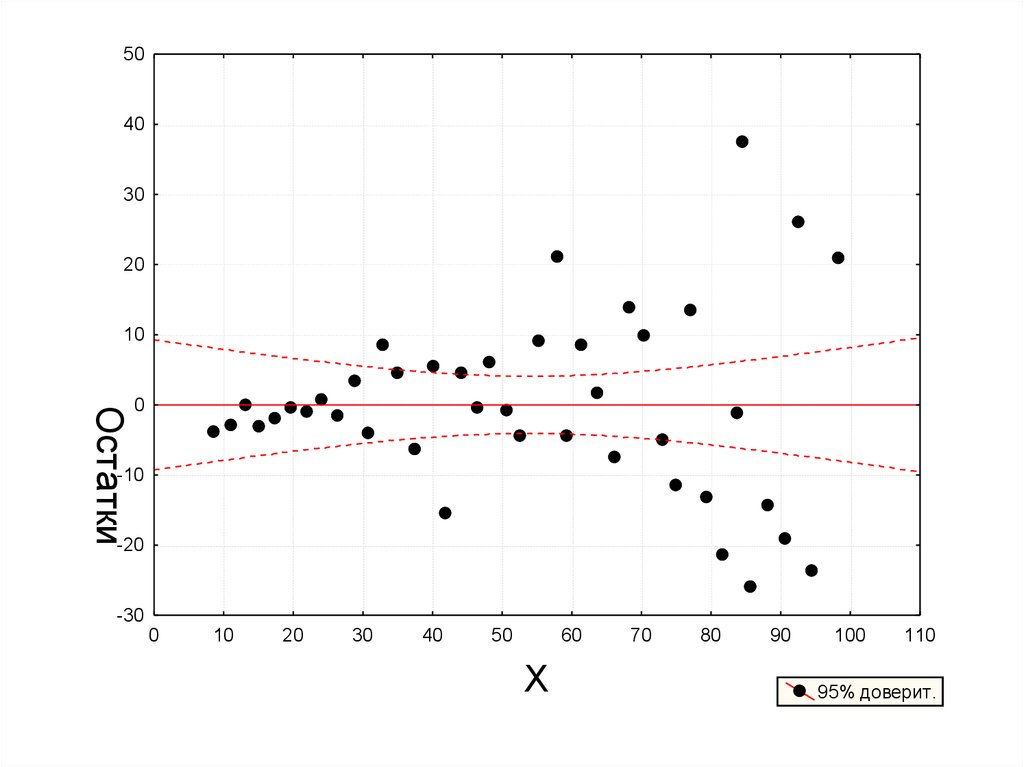
8.
5040
30
20
10
Остатки
0
-10
-20
-30
0
10
20
30
40
50
60
X
70
80
90
100
110
95% доверит.
9.
Пример гетероскедостичности в пространственныхданных: эффект выбросов
X - численность официально зарегистрированных
безработных (чел.)
Y - число зарегистрированных преступлений (ед.).
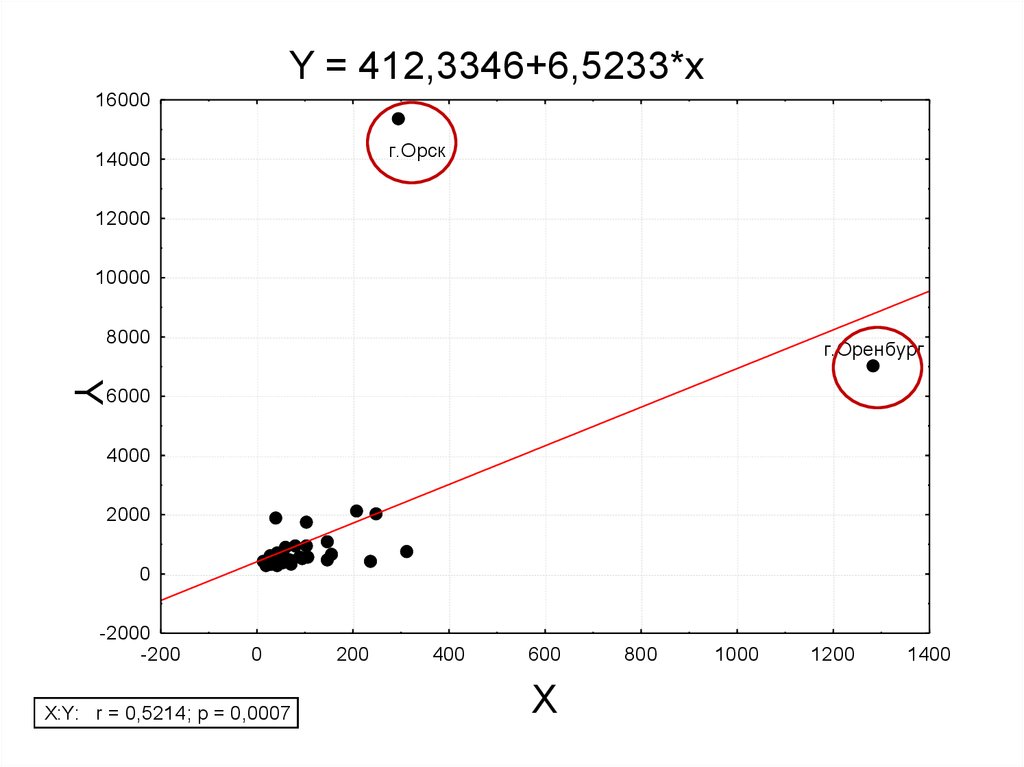
10.
Y = 412,3346+6,5233*x16000
г.Орск
14000
12000
10000
8000
г.Оренбург
Y
6000
4000
2000
0
-2000
-200
0
X:Y: r = 0,5214; p = 0,0007
200
400
600
X
800
1000
1200
1400
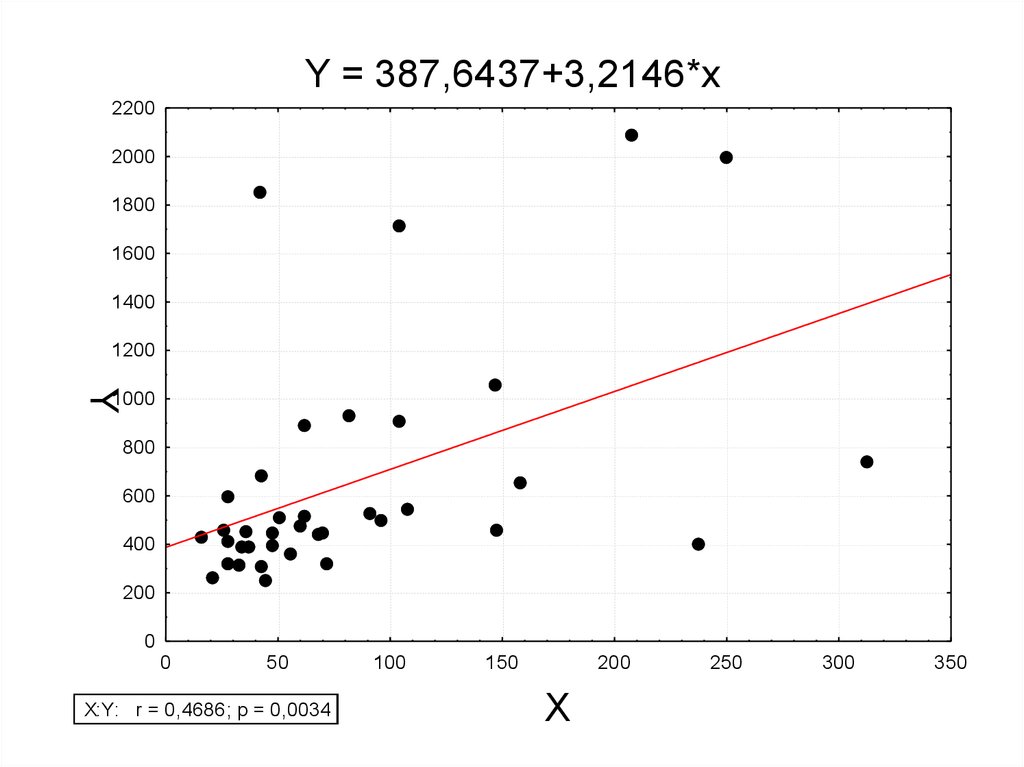
11.
Y = 387,6437+3,2146*x2200
2000
1800
1600
1400
1200
Y
1000
800
600
400
200
0
0
50
X:Y: r = 0,4686; p = 0,0034
100
150
200
X
250
300
350
12.
16001400
1200
1000
800
600
400
200
Остатки
0
-200
-400
-600
-800
-1000
0
50
100
150
200
X
250
300
350
95% доверит.
13.
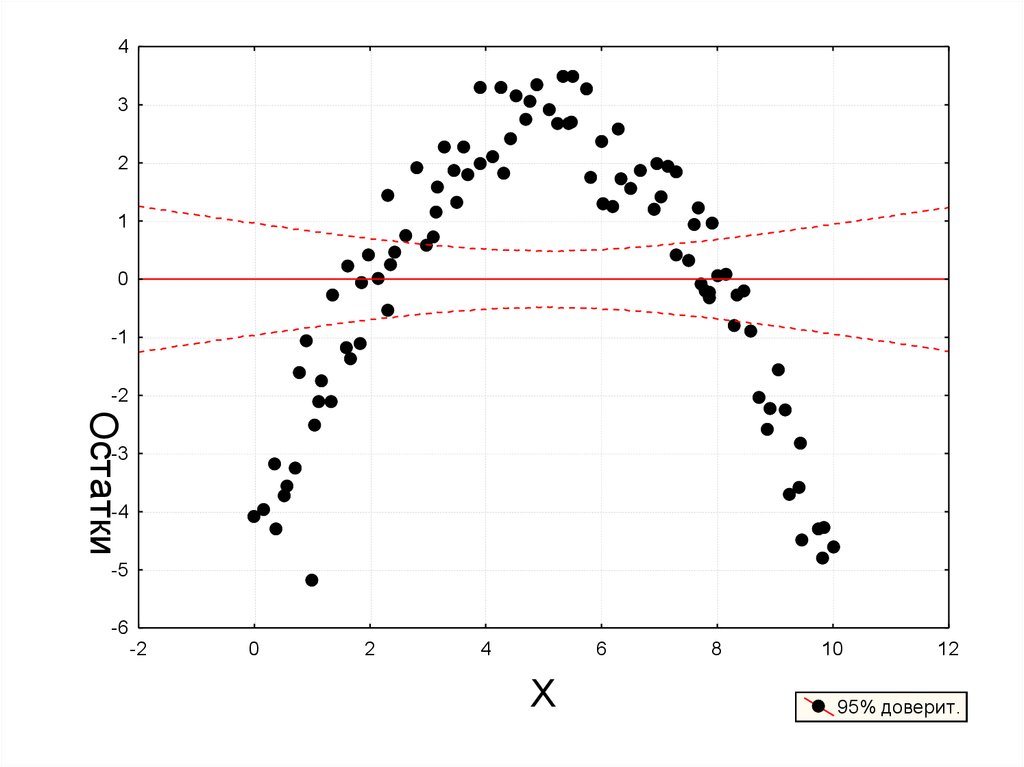
Пример гетероскедостичности в пространственныхданных: неверная спецификация
X – затраты на рекламу
Y – прибыль предприятия
14.
Y = 5,1038+0,5573*x14
12
10
8
Y
6
4
2
0
-2
0
2
4
6
X
8
10
12
15.
43
2
1
0
-1
-2
Остатки
-3
-4
-5
-6
-2
0
2
4
6
X
8
10
12
95% доверит.
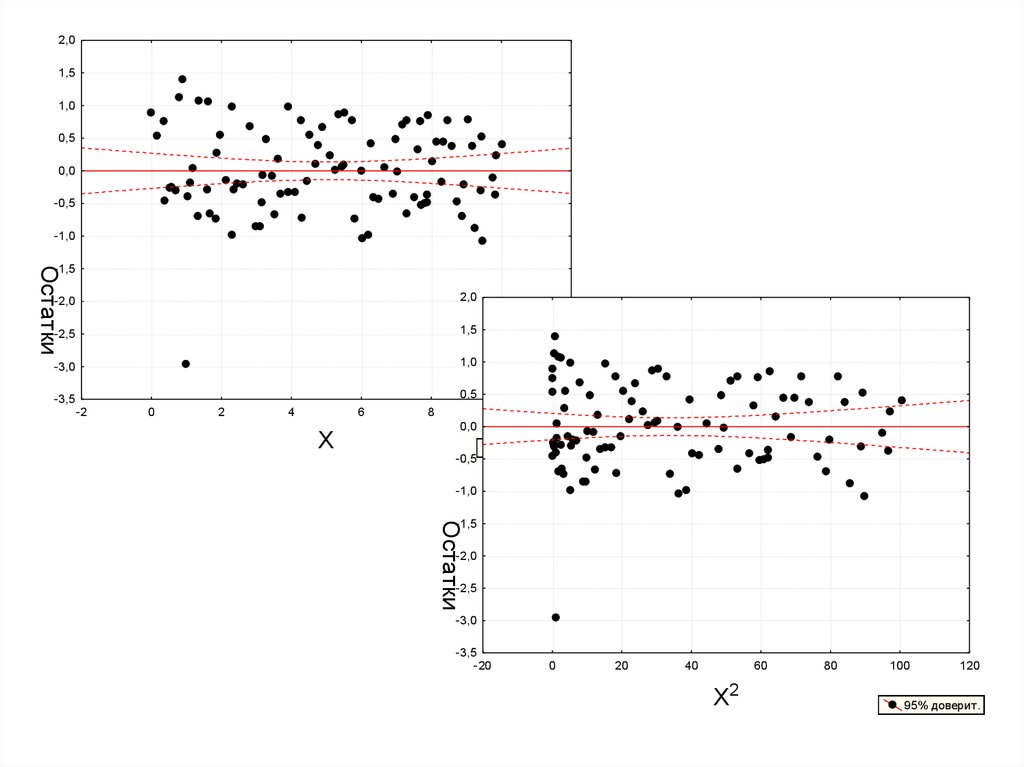
16.
2,01,5
1,0
0,5
0,0
-0,5
-1,0
Остатки
-1,5
-2,0
2,0
-2,5
1,5
-3,0
1,0
0,5
-3,5
-2
0
2
4
6
X
8
10
12
0,0
-0,5
95% доверит.
-1,0
Остатки
-1,5
-2,0
-2,5
-3,0
-3,5
-20
0
20
40
60
X2
80
100
120
95% доверит.
17.
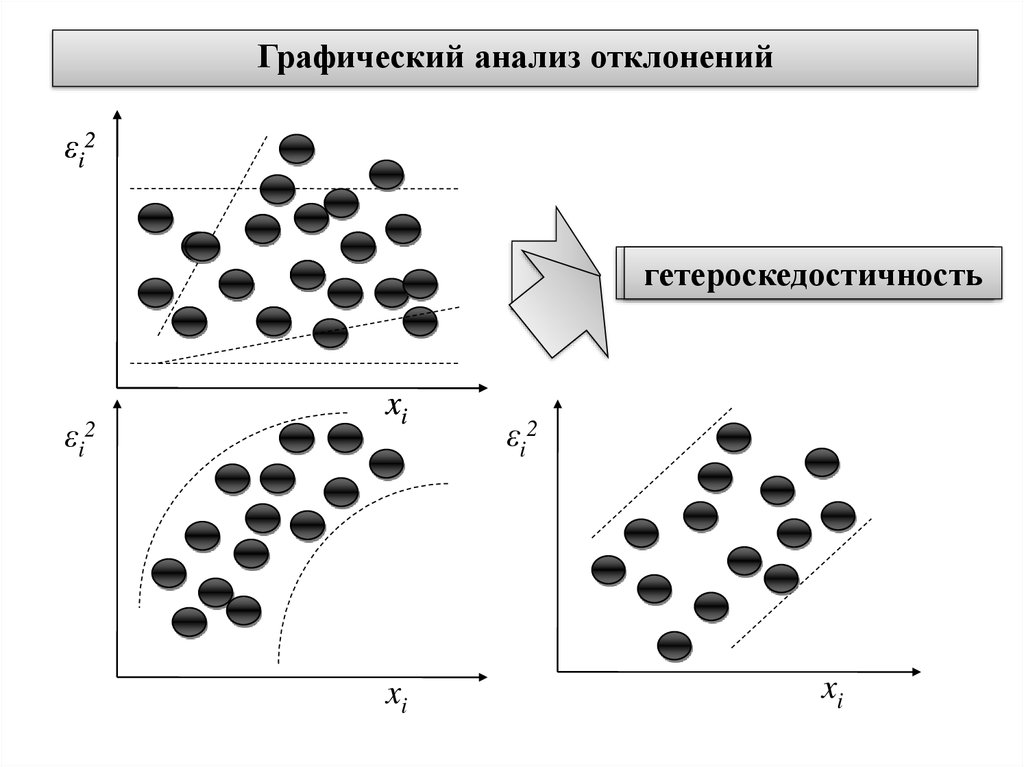
Методы обнаружения гетероскедастичностиграфический анализ отклонений
тест ранговой корреляции Спирмена
тест Парка
тест Глейзера
тест Голдфреда-Квандта
тест Уайта
18.
Графический анализ отклоненийε i2
гетероскедостичность
гомоскедостичность
εi2
xi
xi
ε i2
xi
19.
Тест ранговой корреляции Спирмена1 этап. Значения xi и εi ранжируются. Затем определяется
коэффициент по формуле:
RiX, Ri - ранги по независимой переменной и случайным
отклонениям;
n – объем изучаемой совокупности.
2 этап. Находится t-фактическое по формуле:
3 этап. tфакт сравнивается tтабл (α/2; v=n-2). Если tфакт > tтабл то
необходимо отклонить гипотезу об отсутствии
гетероскедостичности
20.
Тест Парка1 этап. Строится уравнение регрессии:
2 этап. Для каждого наблюдения определяется:
3 этап. Строится регрессионное уравнение:
4 этап. Проверяется статистическая значимость коэффициента
β на основе t-статистики.
Если коэффициент β значим, то это означает наличие связи
между
т.е.
гетероскедостичности в статистических данных
присутствует
21.
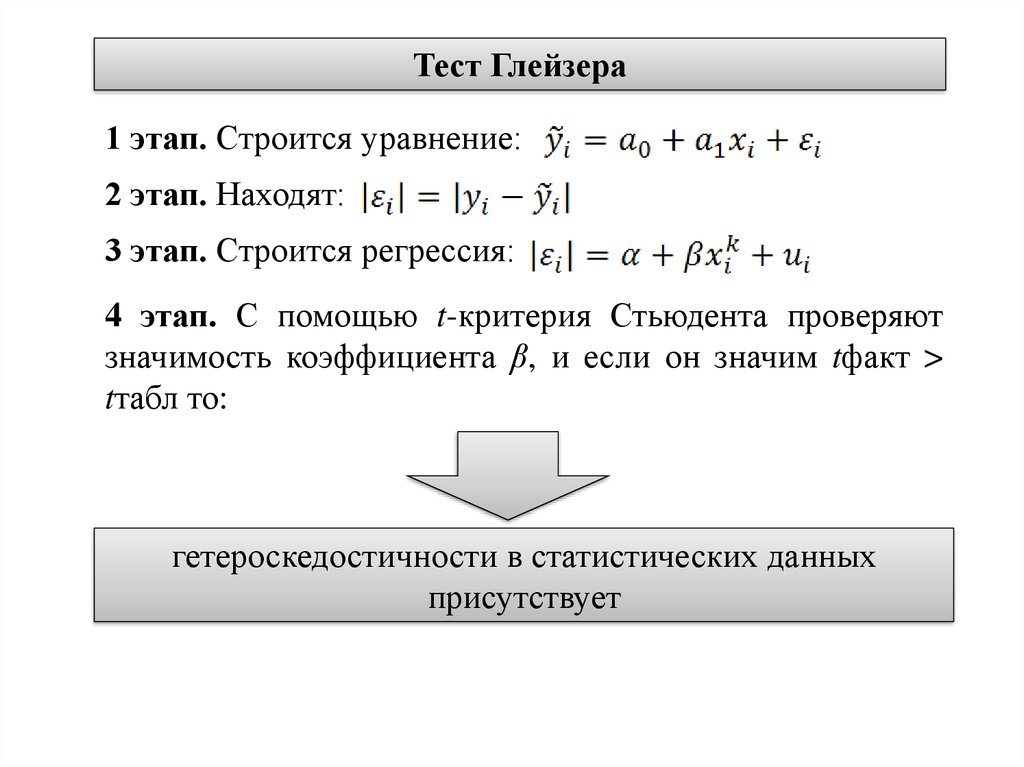
Тест Глейзера1 этап. Строится уравнение:
2 этап. Находят:
3 этап. Строится регрессия:
4 этап. С помощью t-критерия Стьюдента проверяют
значимость коэффициента β, и если он значим tфакт >
tтабл то:
гетероскедостичности в статистических данных
присутствует
22.
Тест Гольфельда-Квандта1 этап. Все n наблюдений упорядочиваются по величине X.
2 этап. Вся упорядоченная выборка после этого разбивается
на три подвыборки размером k, (n-2k), k соответственно.
3 этап. Оцениваются отдельные регрессии для первой
подвыборки (k первых наблюдений) и для третьей подвыборки
(k последних наблюдений).
4 этап. Для сравнения соответствующих дисперсий строится
F- статистика:
где: m - число объясняющих переменных в уравнении
регрессии.
5 этап. Если Fфакт > Fтабл (α, v1=v2=k-m-1), то гипотеза об
отсутствии гетероскедостичности отклоняется.
23. Метод взвешенных наименьших квадратов
разделим обе частиуравнения на:
При этом для ui выполняется условие гомоскедастичности.
24.
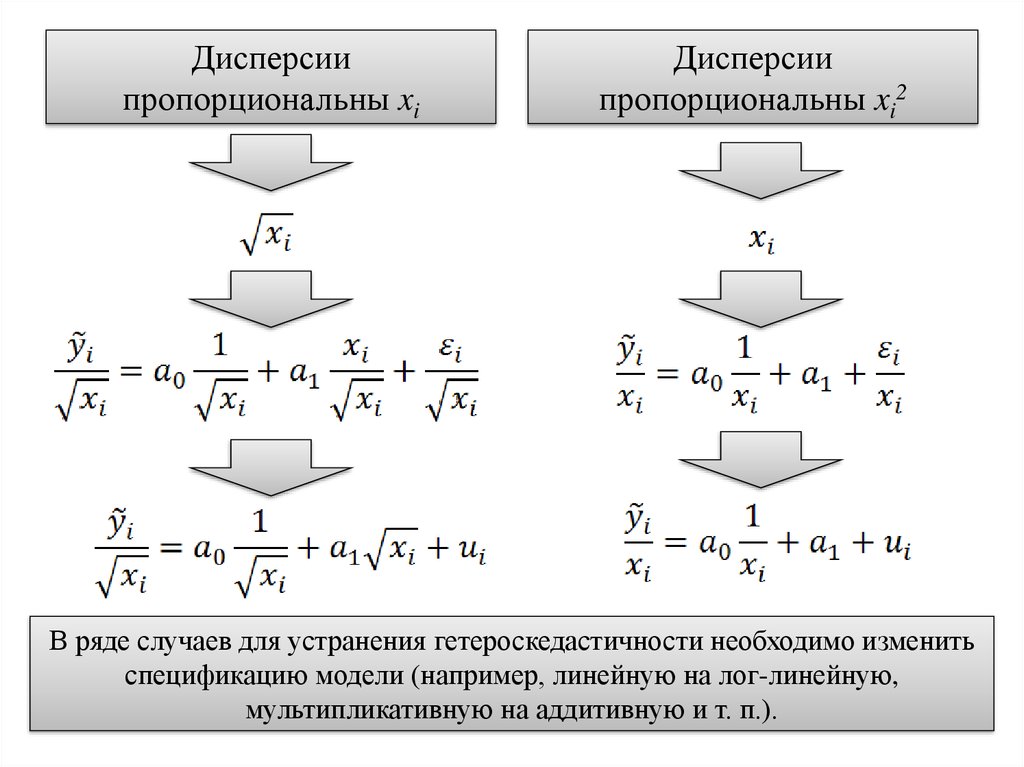
Дисперсиипропорциональны xi
Дисперсии
пропорциональны xi2
В ряде случаев для устранения гетероскедастичности необходимо изменить
спецификацию модели (например, линейную на лог-линейную,
мультипликативную на аддитивную и т. п.).















 Математика
Математика








