Лекция_Аппроксимация

1. Тема 4. Аппроксимация и интерполяция данных в Scilab

1

2. 1. Построение моделей по результатам эксперимента.

Любому специалисту в своей практической
деятельности приходится изучать зависимости
между различными параметрами исследуемых
объектов, процессов и систем.
Из всех способов задания зависимостей наиболее
удобным является аналитический способ задания
зависимости в виде функции y=f(х).
2

3.

Однако на практике специалист чаще всего
получает зависимости между исследуемыми
параметрами экспериментально.
В этом случае ставится натурный эксперимент,
изменяются значения параметров на входе системы
и значения параметров на выходе системы.
Результаты измерений заносятся в таблицу.
В результате проведения натурного эксперимента
получается зависимость между исследуемыми
параметрами в виде таблицы, табличная функция.
3

4.

Затем с этой табличной функцией необходимо
вести
научно-исследовательские
расчеты.
Например, необходимо проинтегрировать или
продифференцировать табличную функцию и т.д.
При такой постановке задачи моделирования
нужно
заменить
табличную
функцию
аналитической.
Для
этой
цели
используются
аппроксимации и интерполяции.
методы
4

5. 2. Математические определения

Аппроксимация – это замена исходной
функции f(x) функцией φ(x) так, чтобы отклонение
f(x) от φ(x) в заданной области было наименьшим.
Функция φ(x) называется аппроксимирующей.
5

6.

6

7.

30.59
40
30
Y
20
g ( t)
10
7.3
0
1
1
1.5
2
2.5
3
3.5
4
X t
4.5
5
5
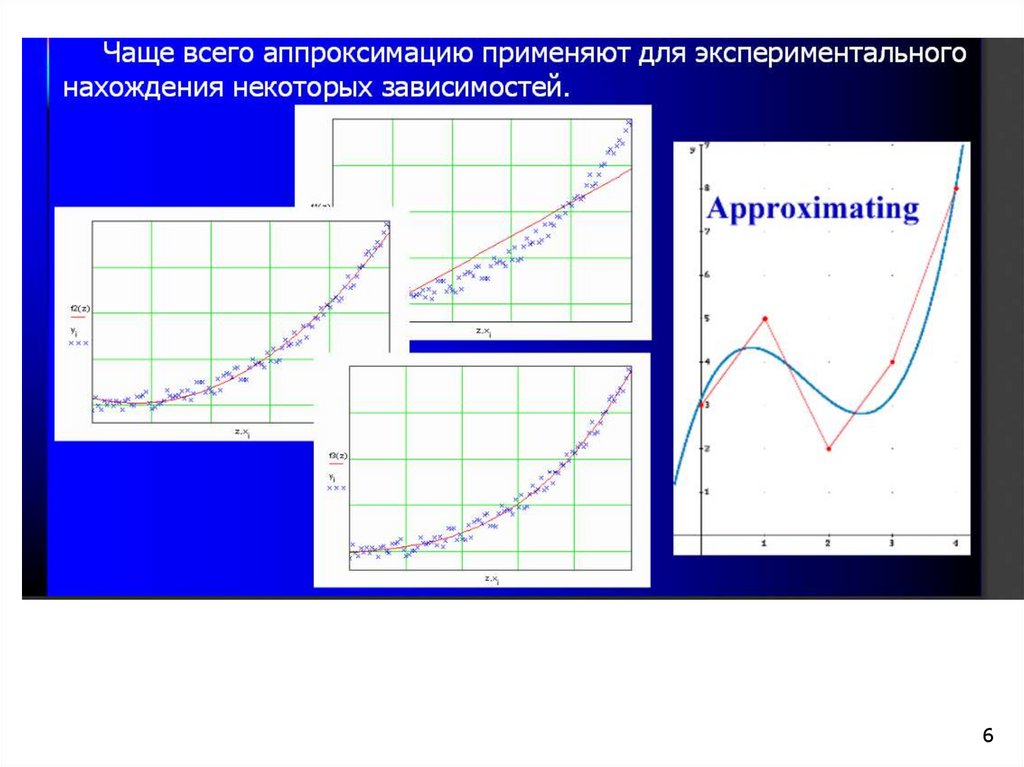
X, Y – экспериментальные данные
g(t) – аппроксимирующая функция
7

8.

Если исходная функция f(x) задана таблично
(дискретным набором точек), то аппроксимация
называется дискретной.
Если
исходная
функция
f(x)
задана
аналитически (на отрезке), то аппроксимация
называется непрерывной или интегральной.
8

9.

При решении задач аппроксимации
используются функции регрессии.
часто
Регрессия – представление совокупности данных
некоторой функцией f(x).
Задачей
регрессии
является
вычисление
параметров функции f(x) таким образом, чтобы
функция
приближала
последовательность
исходных точек с наименьшей погрешностью.
9

10.

При этом функция f(x) называется
уравнением регрессии.
При регрессии не требуется чтобы функция
проходила через все заданные точки, что
особенно важно при аппроксимации данных,
заведомо содержащих ошибки.
10

11.

Основной мерой отклонения функции φ(x) от
функции f(x) при аппроксимации является
величина, равная сумме квадратов разностей
между значениями аппроксимирующей и
исходной функций в заданных точках.
11

12.

Интерполяция – это замена исходной функции
f(x) функцией φ(x) так, чтобы φ(x) точно
проходила через заданные точки исходной
функции f(x).
Интерполяция
аппроксимацией.
еще
называется
точечной
Точки исходной функции f(x) называются
узлами интерполяции.
12

13.

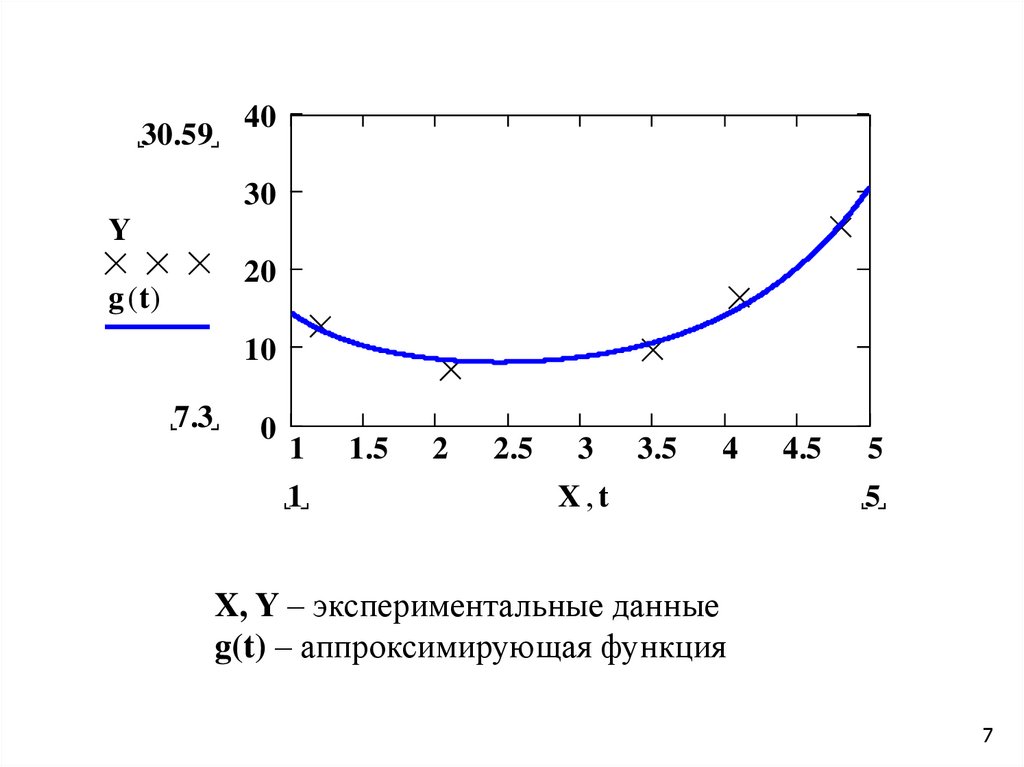
Пример интерполяции.
19.85
20
10
Yi
yy ( xx)
0
6.4 10
0
0
2
4
6
8
Xi xx
10
10
Xi, Yi – экспериментальные данные
yy(xx) – интерполирующая функция
13

14.

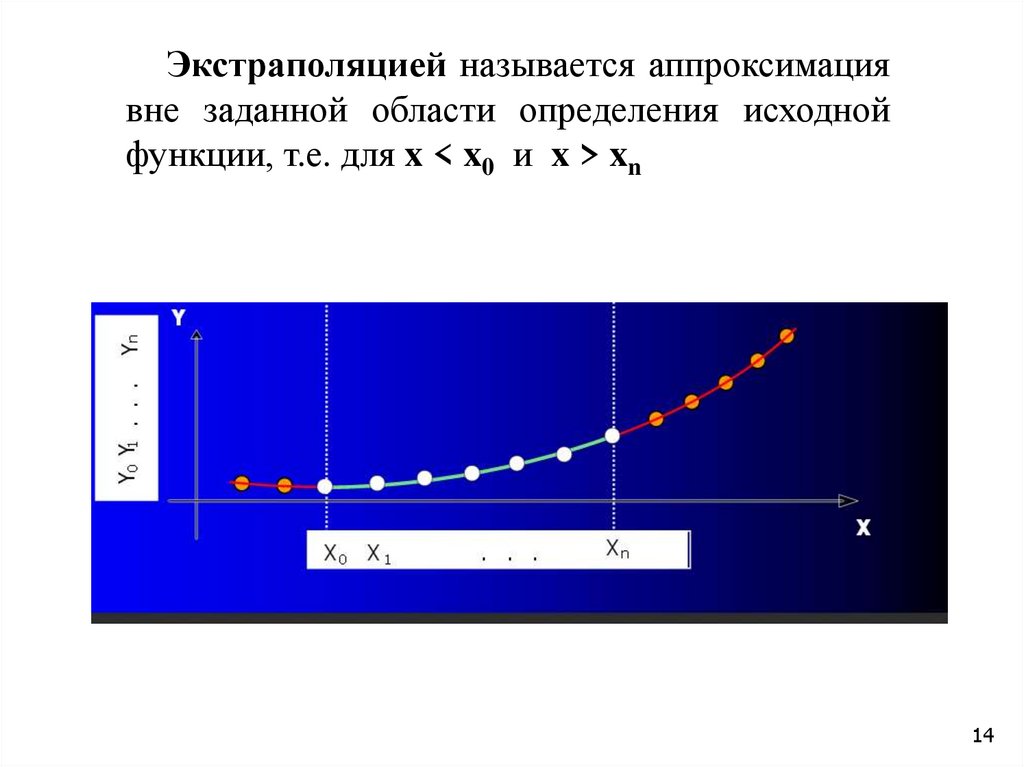
Экстраполяцией называется аппроксимация
вне заданной области определения исходной
функции, т.е. для x < x0 и x > xn
14

15.

Найдя интерполирующую функцию, можно
вычислить
ее
значения
между
узлами
интерполяции, а также определить значение
функции за пределами заданного интервала
(провести экстраполяцию).
Простейшими видами интерполяции является
линейная и квадратичная.
При линейной интерполяции точки заданной
функции соединяются линейными отрезками, а
при квадратичной – отрезками парабол. Такая
интерполяция называется параболической
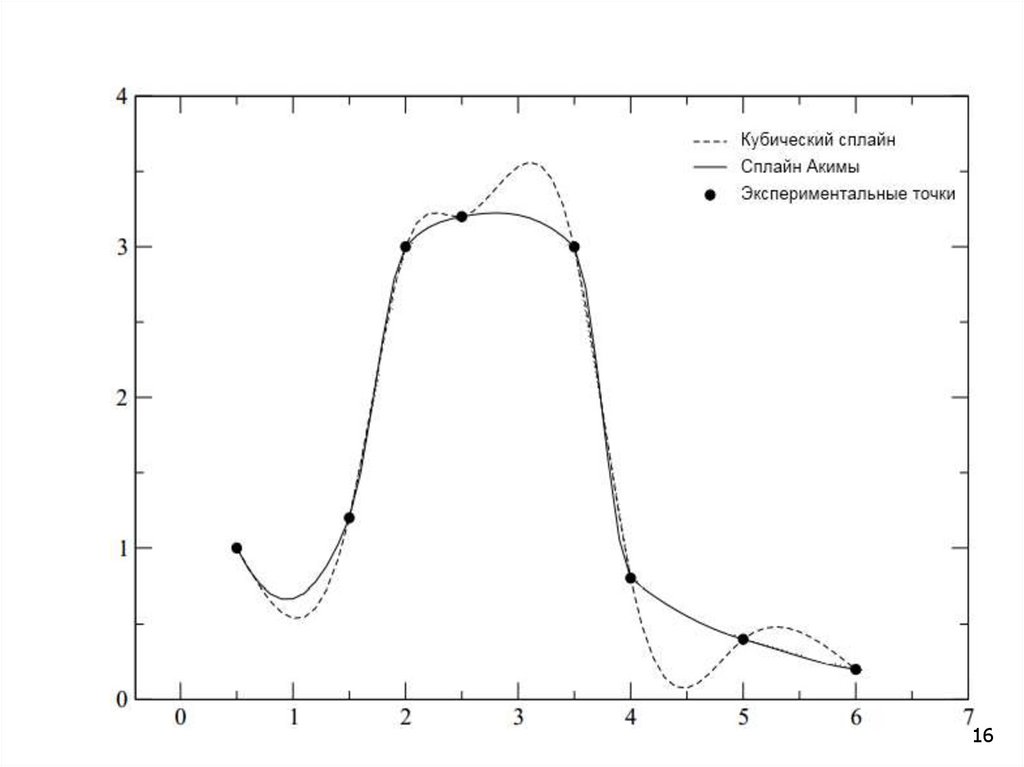
Распространенным
видом
интерполяции
является использование кубических сплайнфункций.
15

16.

16

17.

Интерполяция может выполняться с помощью
многочленов Ньютона, Эрмита, Лагранжа и т.д.
Наиболее
известными
методами
аппроксимации являются метод наименьших
квадратов, метод многочленов Чебышева, рядов
Тейлор и т.д.
17

18.

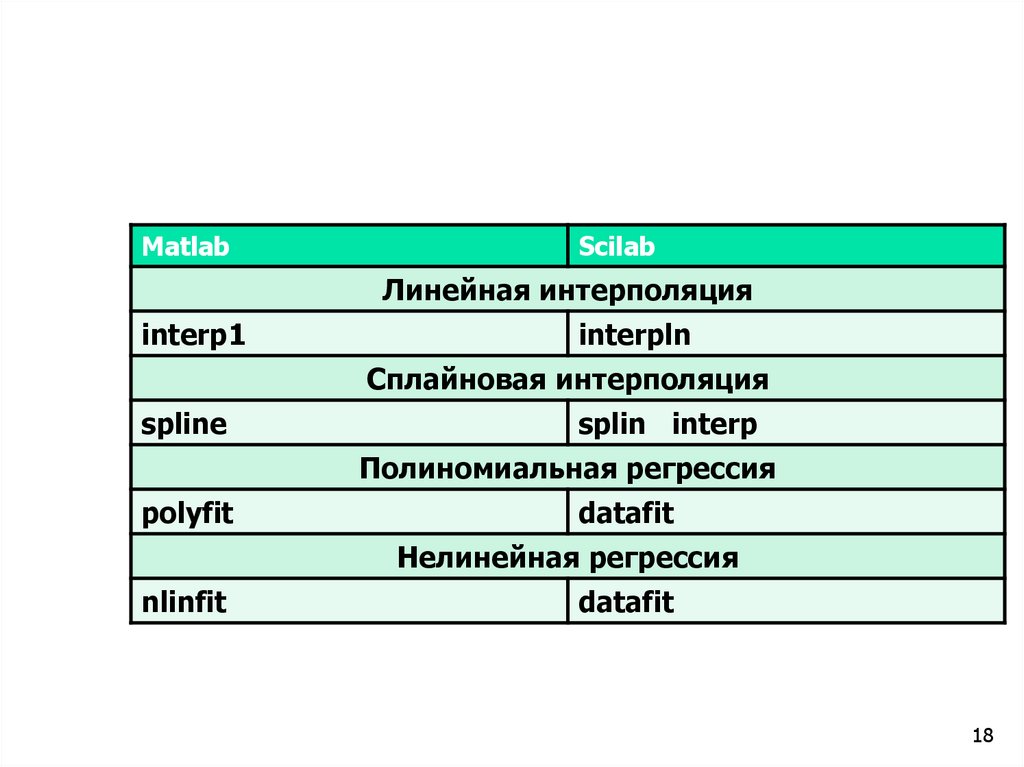
Matlab
Scilab
Линейная интерполяция
interp1
interpln
Сплайновая интерполяция
spline
splin interp
Полиномиальная регрессия
polyfit
datafit
Нелинейная регрессия
nlinfit
datafit
18

19. 3. Функции интерполяции в Scilab

3.1. Линейная интерполяция
Для проведения линейной интерполяции для
таблично заданной функции в Scilab используется
стандартная функция interpln следующего
общего вида:
y= interpln(Z,x)
Значения интерполирующей функции y будут
определены в точках x, и выходной массив будет
иметь ту же размерность, что и массив x.
19

20.

Матрица Z должна иметь две строки, в первой
содержатся значения абсцисс точек исходной
табличной функции, во второй – значения
ординат.
Если исходная функция задана в виде двух
векторов x и y, то их можно объединить в
матрицу так: [x;y].
20

21.

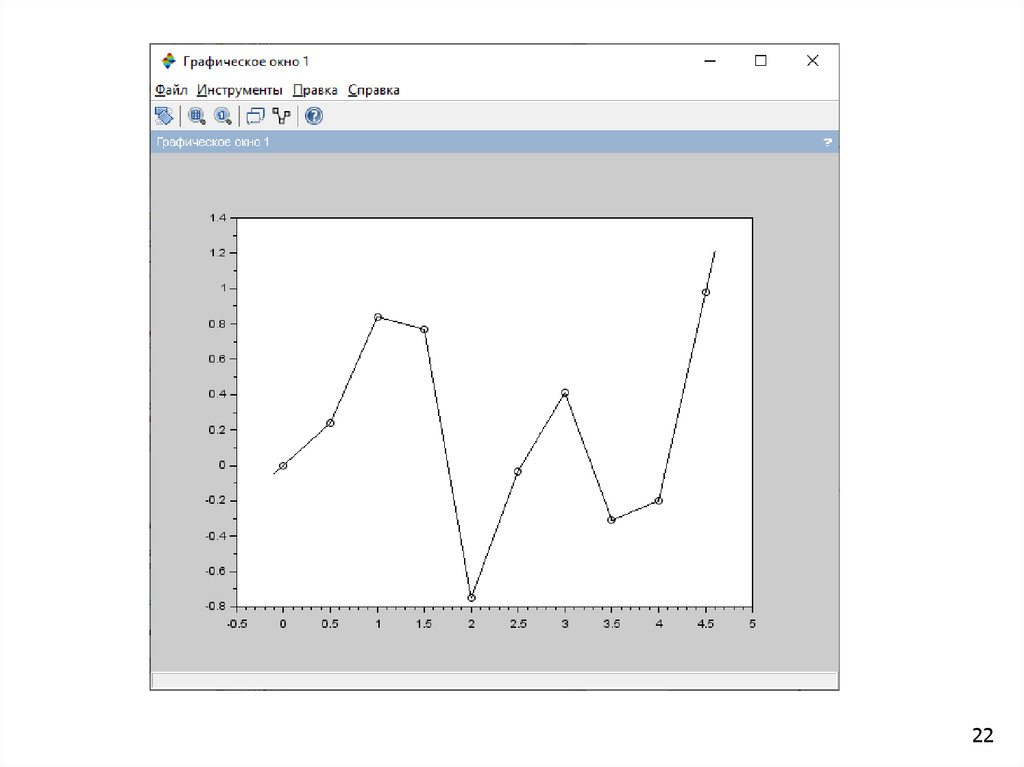
Пример 2. // линейная интерполяция
clear
x=0:0.5:4.5
y=[0 0.24 0.84 0.77 -0.75 -0.033 0.41 -0.31 -0.2 0.98]
xx=-0.1:0.05:4.6
yy=interpln([x;y],xx)
figure(1)
newaxes
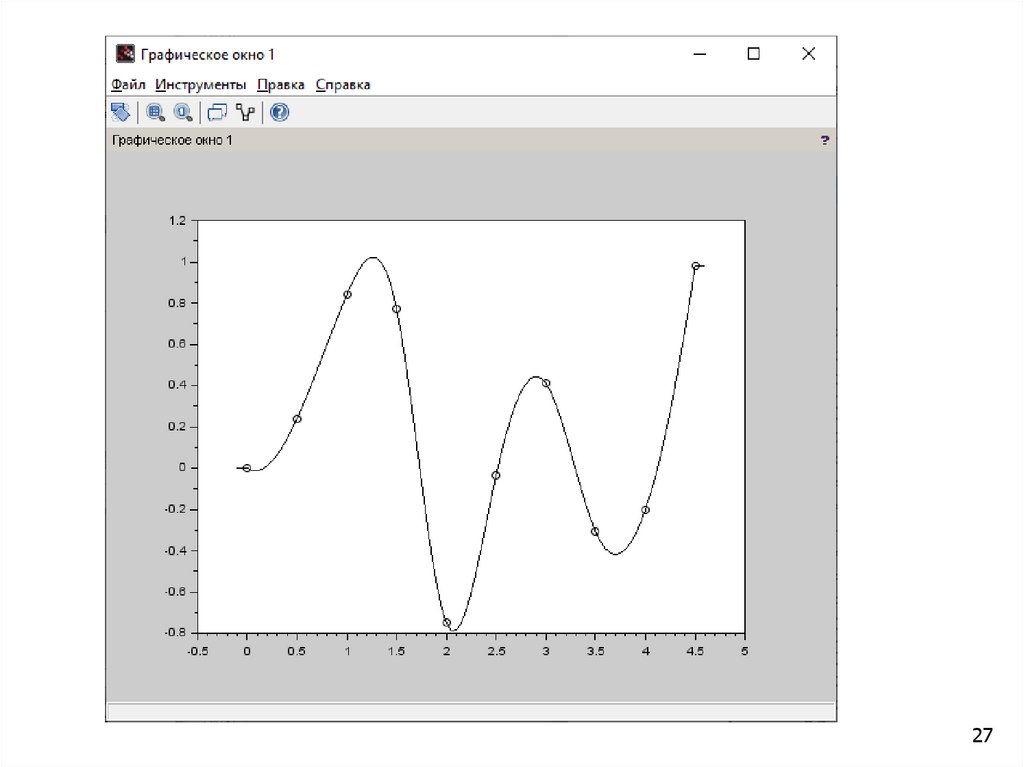
plot(x,y,'ok',xx,yy,'k')
21

22.

22

23.

23

24.

3.2. Интерполяция кубическим сплайном
Для того, чтобы найти значения сплайнфункции для аппроксимации, используется
функция interp.
Y=interp(X,x,y,k)
x, y – координаты исходных точек
X,Y – координаты точек сплайн-функции
k – коэффициенты кубического сплайна
Для определения коэффициентов сплайнинтерполяции используется стандартная функция
k= splin(x,y)
24

25.

Для выполнения сплайн-интерполяции
необходимо:
создать два вектора (х,у) из заданных значений
координат точек
вычислить коэффициенты сплайна
задать вектор значений аргумента, для которых
нужно вычислить значения сплайн-функции
вычислить значения сплайн-функции
построить графики исходной и
интерполирующей функций
25

26.

Пример 2. // сплайн-интерполяция
clear
x=0:0.5:4.5
y=[0 0.24 0.84 0.77 -0.75 -0.033 0.41 -0.31 -0.2 0.98]
k=splin(x,y)
xx= -0.1:0.05:4.6
yy=interp(xx,x,y,k)
figure(1)
newaxes
plot(x,y,'ok',xx,yy,'k')
26

27.

27

28. 4. Функции аппроксимации в Scilab

4.1. Метод наименьших квадратов (МНК)
Для аппроксимации по методу наименьших
квадратов в Scilab используется функция datafit.
Общий вид функции:
datafit(F,Z,b0)
F – имя функции, которая вычисляет разность между
экспериментальными и теоретическими значениями
Z – матрица координат точек исходной функции,
можно использовать [x; y]
b0 – вектор-столбец начальных значений для
коэффициентов аппроксимирующей функции
28

29.

Обращение к функции имеет вид:
[k,s]= datafit(F,[x; y],b0)
k – вектор коэффициентов аппроксимирующей
функции
s – сумма квадратов отклонений исходной
функции от аппроксимирующей в заданных точках
(погрешность вычислений)
Функция F может быть описана любым из двум
возможных способов.
29

30.

4.2. Использование функций в Scilab
Для описания функции есть два способа:
с помощью оператора-функции deff
с помощью подпрограммы-функции function
30

31.

Общий вид оператора-функции deff
deff('y=f(x)','y=<выражение>')
<выражение> – арифметическое выражение,
включающее переменную х
f
–
имя
функции,
которое
использоваться для обращения к ней
будет
x- аргумент или входной параметр функции
y- выходной параметр функции (результат)
31

32.

Если
у
оператора-функции
несколько
выходных параметров, то они объединяются в
вектор, например [y1,y2]
Примеры записи оператора-функции:
deff('y=f(x)','y=cos(x)-0.1*x')
deff('[y1,y2]=z(x)','y1=cos(x)-0.1*x;y2=sin(x)')
32

33.

Обратиться к оператору-функции можно из
любого оператора, например:
Описание функции
deff('y=f(x)','y=cos(x)-0.1*x')
Обращение к функции:
x=5
disp(f(x))
z=f(7)
33

34.

Подпрограмма-функция формируется как отдельная
программная единица и может располагаться в любом
месте в файле основной программы, так и в отдельном
файле.
Общий вид описания:
function <имя результата>= <имя функции>(СП),
операторы
endfunction
34

35.

имя результата – имя переменной, куда
помещается результат работы функции, выходной
параметр
имя функции – имя, по которому выполняется
обращение к функции из вызывающей программы
СП – список формальных
(аргументов) функции
параметров
Можно сохранять функции в отдельных файлах.
Тогда имя файла должно обязательно совпадать
с именем функции. Для ее использования она
должна быть загружена в Scilab командой exec.
exec F77.sce
[k,skv]=datafit(F77,[x;y],nach)
35

36.

Все параметры, указанные в скобках после
имени функции, называются входными, они
передают свои значения в функцию.
Выходной
параметр
или
параметры
указываются сразу после слова function, они
передают свои значения в вызывающую
программу.
36

37.

Функция с одним выходным параметром
function s=summa (a, b, c)
function p=prim(x,y)
function k=kluch (d)
Функция с несколькими выходными
параметрами
function [s,n]=summa (a, b, c)
37

38.

Обращение
к
подпрограмме-функции
выполняется так же, как и к оператору-функции,
например
disp (Summa(a,b,S))
A = Poisk (D,Y,X)
if sum(a,b)>0 r = r+1
38

39.

Параметры, используемые при описании
функции, называются формальными.
Параметры, используемые при вызове
функции, называются фактическими.
function s=summa (a, b, c)
a, b, c – формальные параметры
z=summa(d,x,y)
d,x,y – фактические параметры
39

40.

Пример.
Вычислить сумму квадратов двух заданных чисел.
Использование оператора-функции
deff('x=skv(a,b)','x=a^2+b^2') - описание
z=skv(3,2) - обращение
disp(z)
__________
13
- результат
40

41.

Использование подпрограммы- функции
function x=skv(a, b) - описание
x=a^2+b^2
endfunction
z=skv(3,2) - обращение
______________
13
- результат
41

42.

4.3. Пример использования МНК
При использовании МНК вид аппроксимирующей
функции заранее считается известным. Необходимо
только найти коэффициенты функции.
Выполнить аппроксимацию экспериментальных
данных полиномом третьей степени вида
Необходимо найти коэффициенты K1, K2, K3, K4
Тогда в Scilab функцию аппроксимации можно будет
записать в виде:
Y=k(1)*x.^3+k(2)*x.^2+k(3)*x+k(4),
где k – вектор коэффициентов
42

43.

Для аппроксимации используется функция
datafit (F,Z,b0)
F – имя функции, которая вычисляет разность
между экспериментальными и теоретическими
значениями
х(2)- экспериментальные значения
х(1)- теоретические значения, вычисляемые в
соответствии с видом аппроксимирующей функции
43

44.

// Описание функции:
deff('Y=F(k,x)','Y=x(2)-(k(1)*x(1)^3+k(2)*x(1)^2 +…
k(3)*x(1)+k(4))')
или
function y=F(k, x)
y=x(2)-(k(1)*x(1)^3+ k(2)*x(1)^2+k(3)*x(1) +k(4))
endfunction
44

45.

// создание векторов координат исходных точек
x=[0 0.7 1.4 1.6 2.3 3 3.5 4.2 4.8 5.6 6.3]
y=[0.01 0.1 0.16 0.17 0.12 0.04 -0.04 -0.12 -0.1 -0.08 0]
// установка начальных значений коэффициентов
nach=[0;0;0;0]
// определение коэффициентов аппроксимирующей
//функции (k) и ошибки аппроксимации (skv)
[k,skv]=datafit(F,[x;y],nach)
45

46.

// определение координат точек аппроксимирующей
функции
X=0:0.01:6.5
Y=k(1)*X.^3+k(2)*X.^2+k(3)*X+k(4)
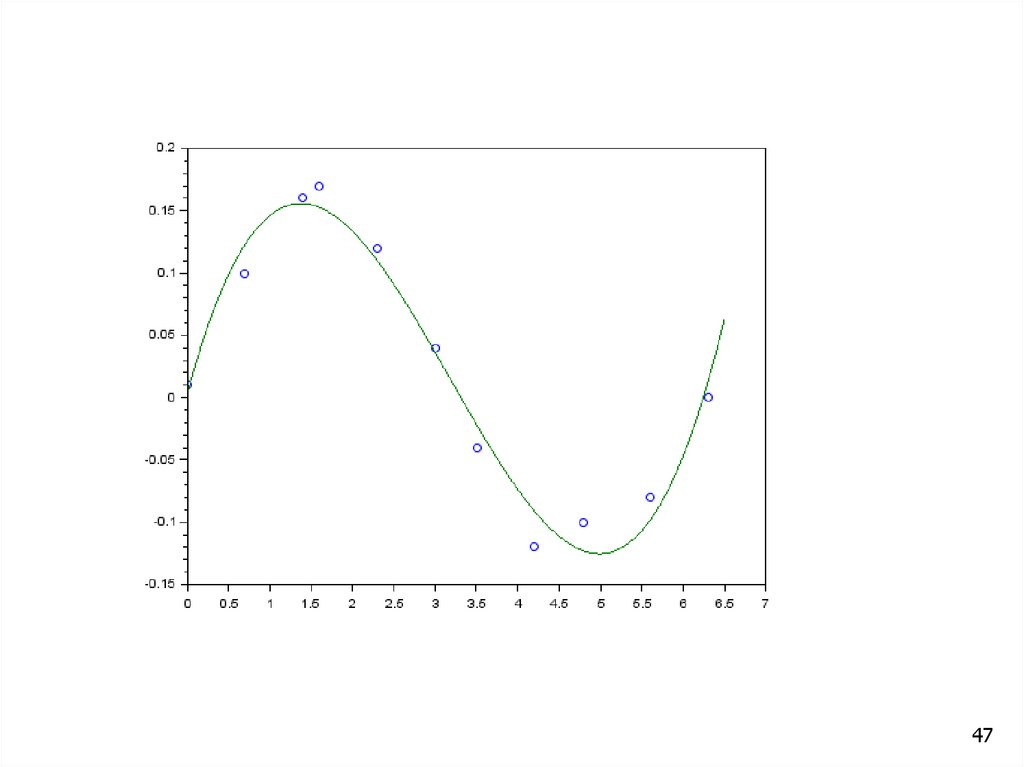
plot(x,y,'o',X,Y)
Вид аппроксимирующей функции:
Y(x)=-5.069e-4 x3+ 0.0182 x2-0.1373 x+0.2724
Среднеквадратичная ошибка аппроксимации
skv=0.003
46

47.

47

48.

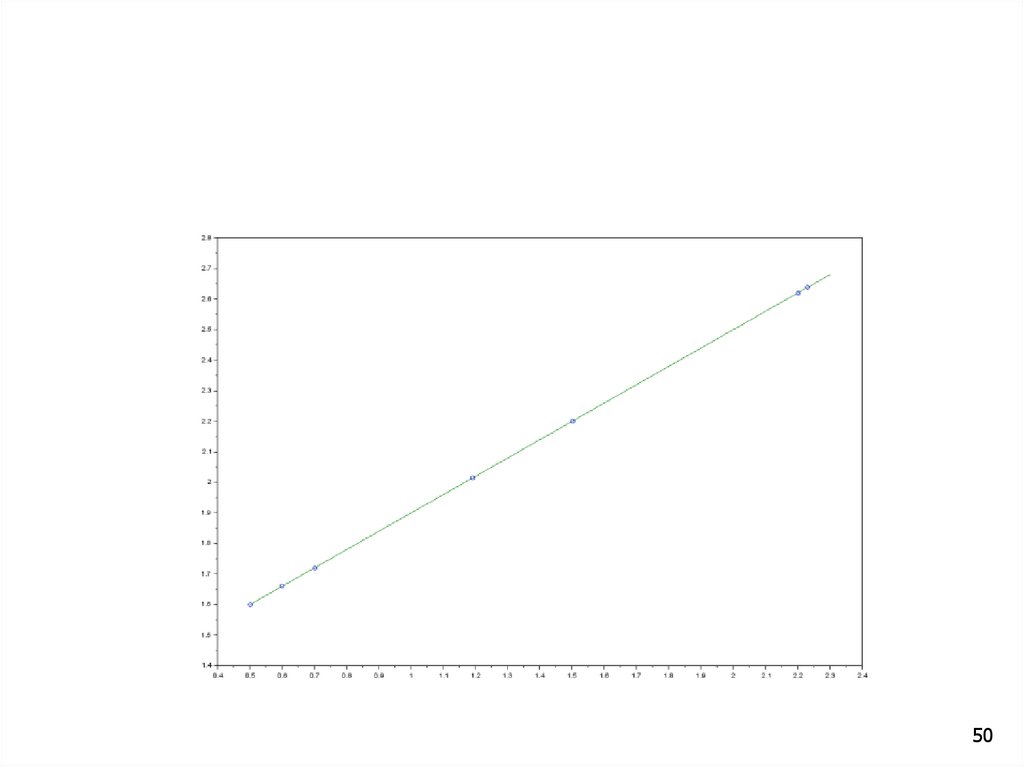
Для определения коэффициентов линейной
регрессии для аппроксимации с помощью функции
вида y(x)=ax+b используется стандартная функция
regline.
Пример:
x=[0.5 0.6 0.7 1.19 1.5 2.2 2.23]
y=[1.6 1.66 1.72 2.014 2.2 2.62 2.638]
[a,b]=reglinе(x,y)
xx=0.5:0.01:2.3
yy=a*xx+b
plot(x, y, 'o',xx,yy)
48

49.

49

50.

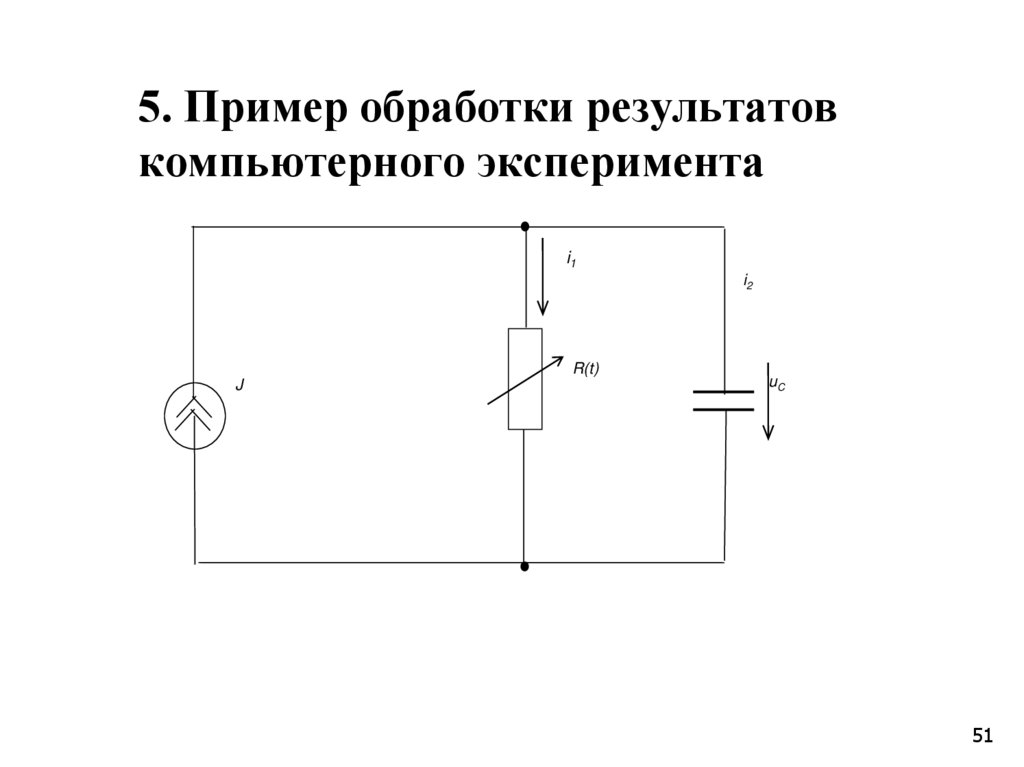
50

51. 5. Пример обработки результатов компьютерного эксперимента

i1
i2
R(t)
J
uC
51

52.

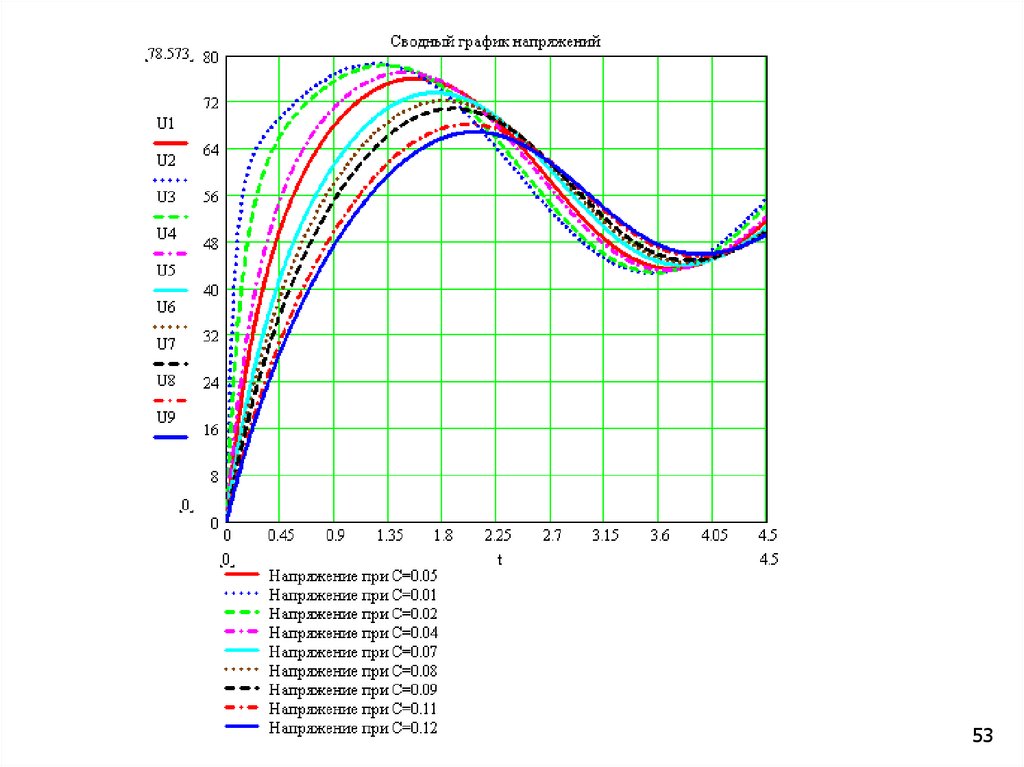
После реализации модели и проведения
экспериментов с моделью получены вектора
U1,U2,…,U9 при различных значениях емкости С,
в которых содержатся значения напряжений в
разные моменты времени.
Вектор варьируемого параметра содержит
значения емкостей, при которых проводились
опыты по модели.
Необходимо
найти
аппроксимирующую
функцию
для
зависимости
максимумов
напряжений от емкости С.
52

53. Пример 1

53

54.

Алгоритм расчета:
сформировать
вектор
максимальные значения
векторов
Umax,
содержащий
элементов исходных
Umax=[Max1, Max2, …, Max11, Max12]
Мах1, Max2,… - максимумы напряжений U1, U2,…
сформировать вектор C значений емкостей, при
которых проводились эксперименты по модели
C=[0.01 0.02 0.04 0.05 … 0.011 0.12]
или С=0.01:0.011:0.12
54

55.

для аппроксимации применить функцию
datafit
В качестве аппроксимирующей функции
использовать полином второй степени
y Ax 2 Bx C
Описание функции:
function y=F(k,x)
y= x(2)-(k(1)*x(1)^2+k(2)*x(1)+k(3))
endfunction
55

56.

Аппроксимация и построение графика
nu=[0;0;0]
[k,skv]=datafit(F,[C;Umax],nu)
disp(k)
disp(skv)
x=0:0.001:0.13
y=k(1)*x.^2+k(2)*x+k(3)
plot(C,Umax,'o',x,y)
56

57.

Коэффициенты вектора k:
- 432.29667
- 47.601046
79.048925
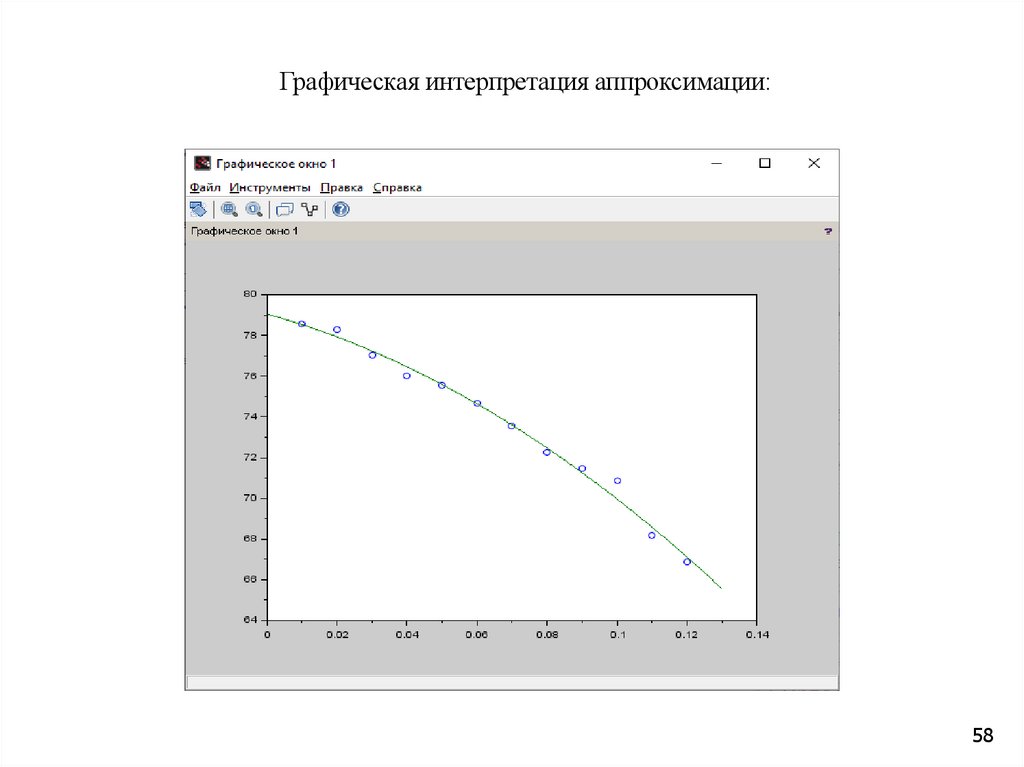
Аппроксимирующая функция:
Y(x)=-432.29 x2 - 47.6 x+79.05
Погрешность skv=1.506
57

58.

Графическая интерпретация аппроксимации:
58