Похожие презентации:
Приближение функций и экспериментальных данных
1.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ ИЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Определение:
Под экспериментальными данными понимается
числовая информация, полученная при измерении
некоторых параметров наблюдаемого процесса
(явления).
Определение:
Аппроксимирующая формула – это эмпирическая
(опытная) формула, построенная при обработке
экспериментальных данных по полученным в ходе
эксперимента данным.
1
Сам способ приближения функции – аппроксимация.
2.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ ИЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Задачи приближения экспериментальной информации:
интерполяция,
сглаживание,
экстраполяция (прогноз).
Определение 1:
Под интерполяцией данных понимают построение
функции, которая как можно ближе проходит через все
значения экспериментальных данных.
Определение 2:
Иногда под интерполяцией понимают получение
2
данных в промежутках между узлами [xi, xi+1].
3.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ ИЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Определение:
Под сглаживание данных понимают получение
функции, устраняющей случайные погрешности,
попавшие в экспериментальные данные.
Определение:
Под экстраполяцией данных (прогноз) подразумевают
предсказание значений функции вне интервала
наблюдения функции.
Как правило, требуется предсказать поведение
функции в будущие моменты времени.
3
4.
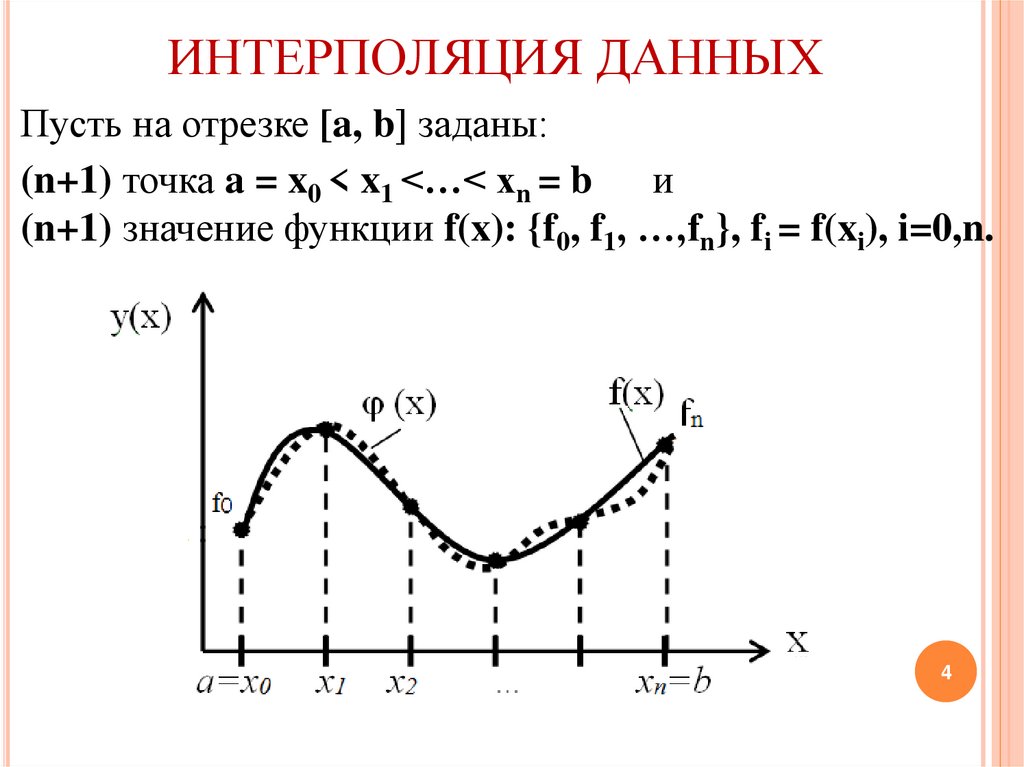
ИНТЕРПОЛЯЦИЯ ДАННЫХПусть на отрезке [a, b] заданы:
(n+1) точка a = x0 < x1 <…< xn = b
и
(n+1) значение функции f(x): {f0, f1, …,fn}, fi = f(xi), i=0,n.
4
5.
ИНТЕРПОЛЯЦИЯ ДАННЫХОбозначения:
Значения xi называются сеткой узлов.
Функция fi – решетчатая функция (таблично заданная).
x
f
x0
f0
x1
f1
…
…
xn
fn
Задача интерполяции: по табличным значениям
{xi, fi} построить функцию (x) такую, что значения
(x) легко вычисляются при x [a, b] и
(xi) = f(xi), i 0,n. - критерий интерполяции
Здесь f(x) – интерполируемая (исходная) функция;
(x) – интерполирующая функция.
5
6.
ИНТЕРПОЛЯЦИЯ ДАННЫХФункция (x) может быть получена в двух видах:
в виде аналитического выражения (формула),
численно, т.е. в виде отдельных числовых
значений для x [a, b].
При получении аналитической зависимости:
(x) строится в виде линейной комбинации
элементарных (базисных) функций: ( x) m a ( x)
k k
k 0
k(x) – базисные функции;
ak – коэффициенты разложения по базисным функциям
6
7.
ИНТЕРПОЛЯЦИЯ ДАННЫХЧаще других используются полиномиальные функции:
m
( x ) a k x k
k 0
Основная задача интерполяции в данном случае:
по известным значениям (xi, fi), i=0,n найти
коэффициенты разложения a0, a1, … , am.
7
8.
СПЛАЙН - ИНТЕРПОЛЯЦИЯОпределение:
Сплайн-функции - это функции, составленные из
отдельных кусков многочленов определенной степени.
Построение:
Между каждыми двумя узлами [xi, xi+1] строится
отдельный многочлен со своими коэффициентами aki.
Особенности:
На всем интервале [a, b] сплайн-функция
непрерывна вместе с несколькими производными.
Это повышает точность интерполяции, сохраняя
8
однотипность математической формулы.
9.
СПЛАЙН - ИНТЕРПОЛЯЦИЯНаиболее популярны полиномиальные сплайны
1,2 и –3го порядков.
Линейный сплайн представляет собой кусочнолинейную функцию.
Для каждого частичного интервала [xi, xi+1] исходная
функция f(x) заменяется линейной функцией
S i ( x) a i b i ( x x i ),
x i x x i 1 ,
i 1,...,n - 1.
9
10.
СПЛАЙН - ИНТЕРПОЛЯЦИЯДля нахождения коэффициентов ai, bi используются
следующие условия:
Si(xi)=fi, i=0,n–1
критерий интерполирования
Si(xi+1)=Si+1(xi+1), i=0,n–2
непрерывность сплайна в узлах
ИЗ УСЛОВИЯ 1: ai=fi, i=0,n–1.
f i 1 f i
ИЗ УСЛОВИЯ 2: b i h ,
i 1, n - 1
10
11.
СПЛАЙН - ИНТЕРПОЛЯЦИЯОпределение:
Параболический сплайн – это функция, склеенная в
узлах интерполяции из полиномов второго порядка.
Свойство:
В узлах интерполяции сплайн имеет непрерывную
производную.
Построение:
На каждом частичном интервале [xi, xi+1] исходная
функция f(x) заменяется квадратичной функцией
S i ( x) a i b i ( x x i ) с i ( x x i ) 2 ,
x i x x i 1 ,
i 1,...,n - 1.
11
12.
СПЛАЙН - ИНТЕРПОЛЯЦИЯДля параболического сплайна неизвестные ai, bi, ci,
i=0,n–1 находятся из условий:
Si(xi)=fi, i=0,n–1
критерий интерполирования
Si(xi+1)=Si+1(xi+1), i=0,n–2
непрерывность сплайна в узлах
S i(xi+1)=S i+1(xi+1), i=0,n–2
непрерывность производной сплайна в узлах
ИЗ УСЛОВИЯ 1: ai=fi, i=0,n–1.
12
13.
СПЛАЙН - ИНТЕРПОЛЯЦИЯПродифференцируем исходное уравнение:
S i ( x) b i 2 с i ( x x i ),
S i ( x i ) b i ,
S i ( x i 1 ) b i 2 с i h i b i 1 ,
h i x i 1 x i .
ПОЛУЧИМ:
b i 1 b i
сi
,
2h i
i 0, n - 1.
Из второго условия следует:
S i ( x i 1 ) b i 2 с i h i c i h i2 S i 1 ( x i 1 ) f i 1 ,
f i 1 f i
bi cihi .
hi
13
14.
СПЛАЙН - ИНТЕРПОЛЯЦИЯПодставим в последнее уравнение значение ci :
2
( f i 1 f i ) b i b i 1 ,
hi
i 0, n - 1.
Имеем n уравнений для определения (n+1)
неизвестного.
Дополнительное (граничное) условие: b0=m0.
где m0 – значение первой производной в левом конце
интервала.
Тогда обозначив
2
mi
(f i 1 f i ),
hi
ПОЛУЧИМ: b i 1 m i b i ,
i 1, n - 1.
i 1, n - 1.
14
15.
СПЛАЙН - ИНТЕРПОЛЯЦИЯОпределение:
Кубический сплайн – это функция, склеенная в узлах из
полиномов третьего порядка.
Свойство:
Интерполяционный полином третьего порядка проходит
через все заданные узлы и имеет непрерывные первую и
вторую производные.
Построение:
На каждом частичном интервале [xi, xi+1]
интерполирующая функция S(x) имеет вид:
S i ( x) a i b i ( x x i ) с i ( x x i ) 2 d i ( x x i ) 3 ,
x i x x i 1 ,
i 1,...,n - 1.
15
16.
СПЛАЙН - ИНТЕРПОЛЯЦИЯДля кубического сплайна неизвестные ai, bi, ci, di,
i=0,n–1 находятся из условий:
Si(xi)=fi, i=0,n–1
критерий интерполирования
Si(xi+1)=Si+1(xi+1), i=0,n–2
непрерывность сплайна в узлах
S i(xi+1)=S i+1(xi+1), i=0,n–2
непрерывность производной сплайна в узлах
S i(xi+1)=S i+1(xi+1), i=0,n–2
непрерывность второй производной сплайна
в узлах
16
17.
СПЛАЙН - ИНТЕРПОЛЯЦИЯДля нахождения коэффициентов сплайна формируется
система линейных алгебраических уравнений с
трехдиагональной матрицей:
hi
h h i 1
h
Mi i
M i 1 i 1 M i 2 y i 1 y i
6
3
6
где yi=fi+1–fi.
Эффективным способом решения таких систем
является метод прогонки.
17
18.
СПЛАЙН - ИНТЕРПОЛЯЦИЯПосле определения Mi коэффициенты di, ci, bi
находятся из обычных алгебраических выражений:
M i 1 M i
di
,
6h i
Mi
ci
,
2
M i 1 2M i
bi yi
,
6h i
ai fi .
18
19.
ИНТЕРПОЛЯЦИЯ В ППП MATHCAD19
20.
ИНТЕРПОЛЯЦИЯ В ППП MATHCAD20
21.
ИНТЕРПОЛЯЦИЯ В ППП MATHCADLspline, pspline, cspline – интерполяция
линейными, параболическими и кубическими
сплайнами.
Процедуры lspline, pspline, cspline позволяют получить
коэффициенты сплайн-функции 1-го, 2-го и 3-го
порядков, которые являются входной информацией
процедуры interp, производящей интерполяцию между
узловыми значениями.
21
22.
ИНТЕРПОЛЯЦИЯ В ППП MATHCADОписание функций
Аргументы функций
LL:= Lspline(x,y)
PP:=Pspline(x,y)
CC:= Cspline(x,y)
Возвращает вектор
коэффициентов
(производных) сплайна.
х, y – векторные значения
аргумента и функции.
interp (PP, x,y, z)
Возвращает значения
интерполяции для
независимого аргумента z.
z – значения аргумента, в
которых необходимо
выполнить интерполяцию.
22
23.
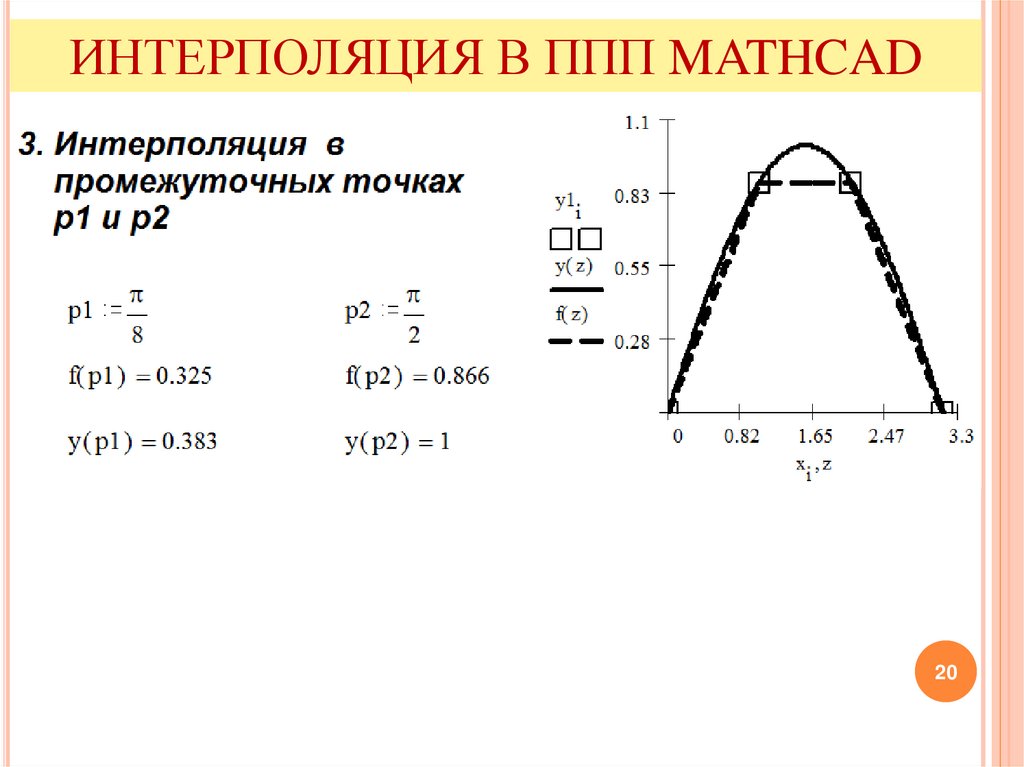
ИНТЕРПОЛЯЦИЯ В ППП MATHCADЗАМЕЧАНИЯ:
1. Вектора х, y должны быть одной размерности.
2. Новый аргумент z может быть непрерывной
переменной, либо также представлять собой векторные
значения.
3. В узлах интерполирующая функция полностью
совпадает с исходной.
4. Вне узлов функции могут значительно различаться.
Это подтверждает расхождение функций в
промежуточных точках р1 и р2.
23
24.
ИНТЕРПОЛЯЦИЯ В ППП MATHCAD24
25.
ИНТЕРПОЛЯЦИЯ В ППП MATHCAD25
26.
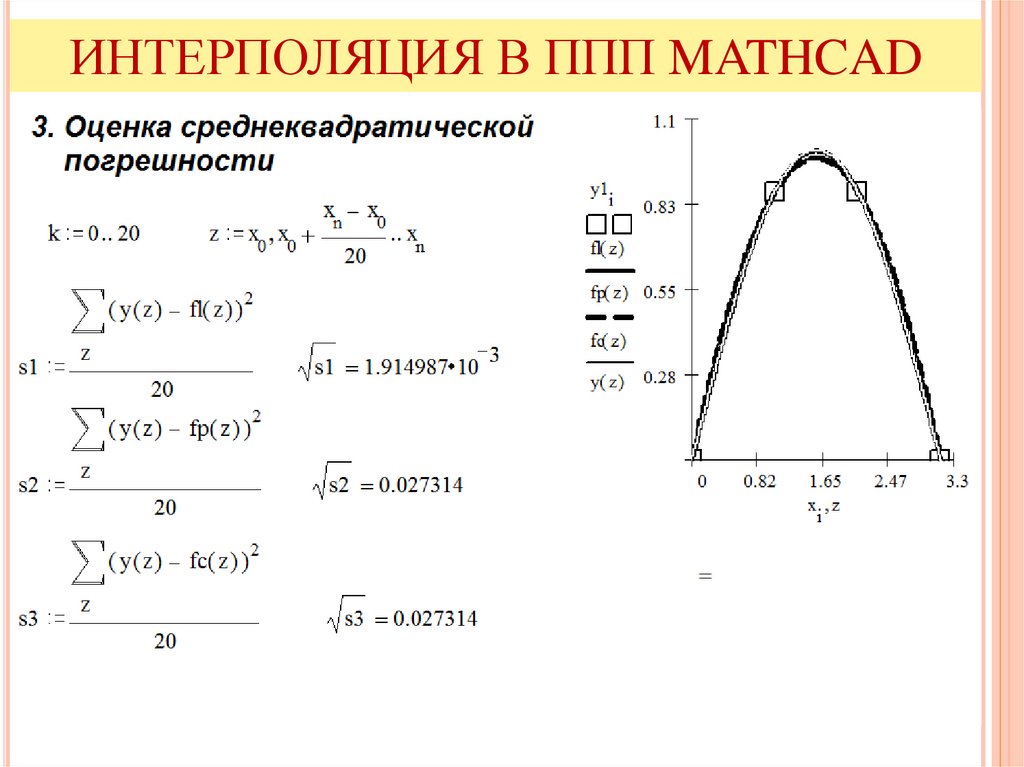
ИНТЕРПОЛЯЦИЯ В ППП MATHCADЗАМЕЧАНИЯ:
1. Результаты интерполяции различными сплайнами
практически не отличаются во внутренних точках
интервала и совпадают с точными значениями
функции.
2. Отличие более заметно при отсутствии узлов
интерполяции в местах изменения функции.
3. Для количественной оценки интерполяции выбрана
среднеквадратическая приведенная погрешность.
26
27.
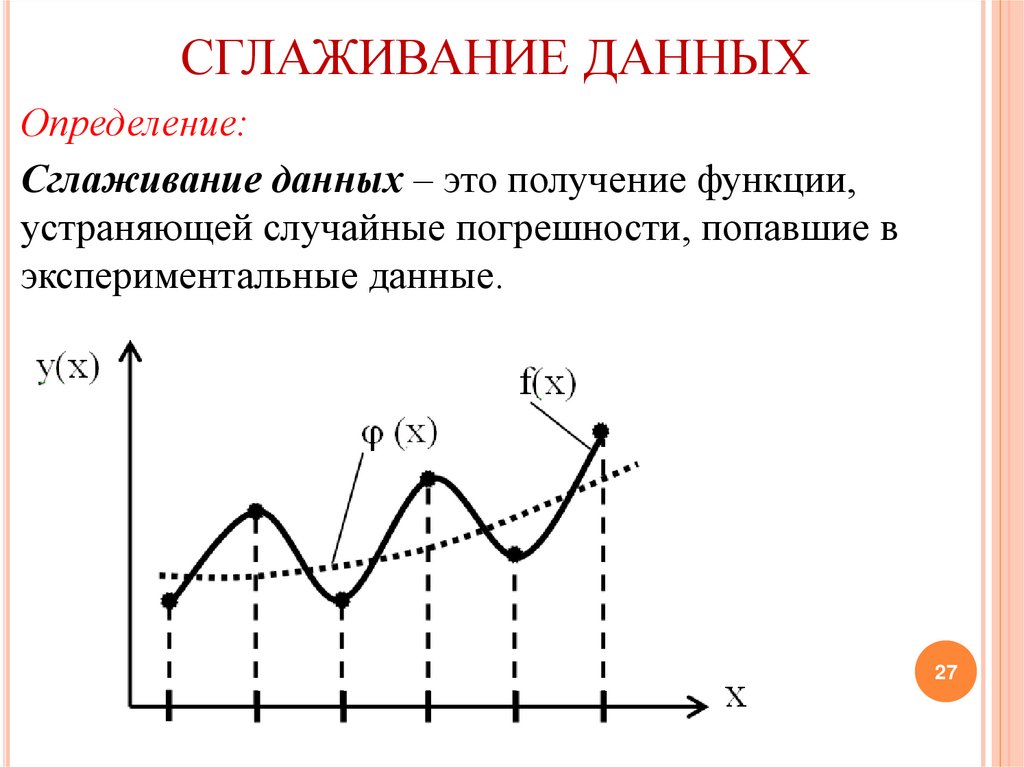
СГЛАЖИВАНИЕ ДАННЫХОпределение:
Сглаживание данных – это получение функции,
устраняющей случайные погрешности, попавшие в
экспериментальные данные.
27
28.
СГЛАЖИВАНИЕ ДАННЫХВарианты сглаживания данных:
1. Получение аналитической функции, позволяющей
строить функцию при любых значениях аргумента;
2. Получение числовых значений функции, более
гладких, чем исходные данные, но только при
исходных значениях аргумента.
Регрессионная функция является оптимальной в
среднеквадратическом смысле.
Графически это означает построение линии
визуально усредняющей экспериментальные
28
данные.
29.
СГЛАЖИВАНИЕ ДАННЫХВ пакете MathСad для получения регрессионного
полиномиального уравнения предназначена процедура
regress():
Описание функции
regress (x,y, k)
Возвращает значения
коэффициентов полинома
Аргументы функции
х, y – векторные
значения аргумента и
функции.
k – степень полинома.
Вектора х, y должны быть одной размерности.
Их значения должны быть упорядочены.
29
30.
СГЛАЖИВАНИЕ ДАННЫХ30
31.
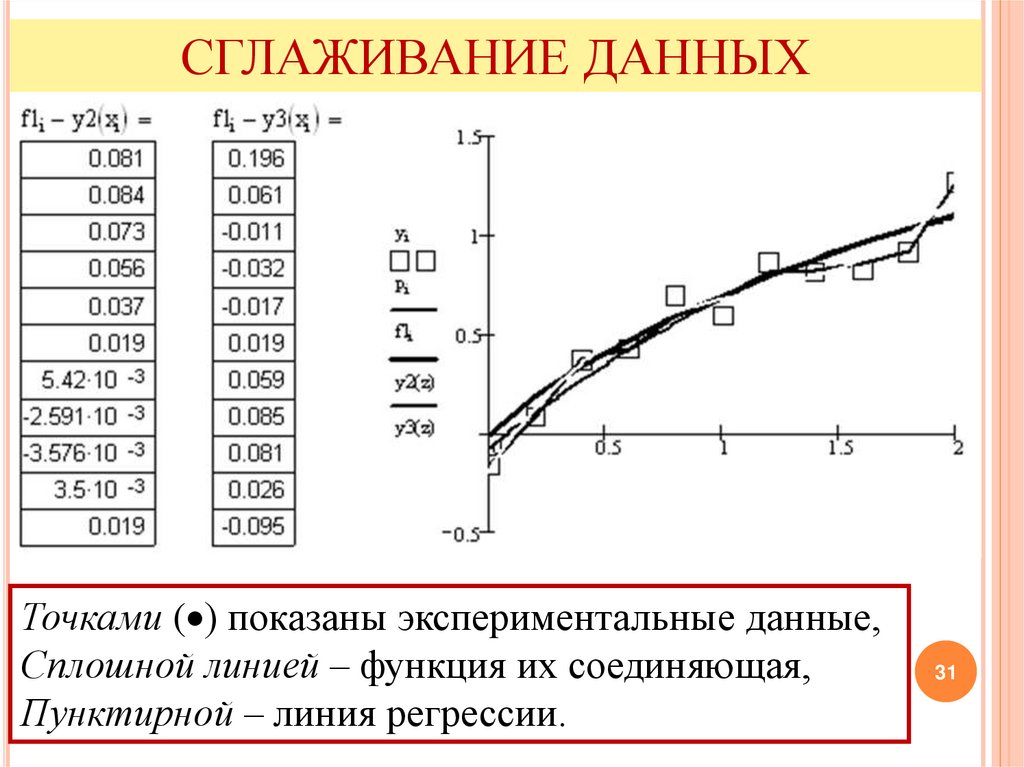
СГЛАЖИВАНИЕ ДАННЫХТочками ( ) показаны экспериментальные данные,
Сплошной линией – функция их соединяющая,
Пунктирной – линия регрессии.
31
32.
СГЛАЖИВАНИЕ ДАННЫХz0, z1 - служебная информация,
z2 – степень полинома,
z3, z4, z5, z6 – коэффициенты полинома,
f1 - дискретные значения исходной функции в точках,
y – исходная функция в условиях помех,
y2, y3 сглаживают зашумленную исходную функцию.
32
33.
СГЛАЖИВАНИЕ ДАННЫХДля получения сглаживания в виде набора значений в
Mathcad предназначены процедуры:
medsmooth;
ksmooth;
supsmooth.
medsmooth(y,k) позволяет получить значения,
сглаженные с помощью скользящей медианы.
y – вектор исходных данных (значения функции);
k – ширина окна сглаживания.
33
34.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВЕсли требуется построить сглаживающую
функцию по произвольному базису, целесообразно
использовать метод наименьших квадратов (МНК).
Идея МНК:
Построение регрессионной функции (x),
оптимальной в среднеквадратическом смысле.
Пусть на сетке узлов {a=x0, x1, …,xn=b} заданы
отсчеты функции yi=y(xi), i=1,n.
Аппроксимирующая функция (x) представляет собой
линейную комбинацию произвольных базисных
34
функций { j(x)}, j=1,m, m<n.
35.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ( x) a 0 0 ( x) a 1 1 ( x) ... a m m ( x)
Неизвестные - коэффициенты aj j=1,m.
Оценку параметров a0, a1, …, am определяем из условия:
n
S(a 0 , a 1 ,..., a m ) ( ( x i ) y i ) 2 min
i 0
- среднеквадратический
критерий
Среднеквадратический критерий означает:
Минимум суммы квадратов отклонений измеренных
значений yi=y(xi) от расчетных (xi).
35
36.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВДля выполнения критерия необходимо, чтобы функция
невязок S(a0, a1,…,am) имела стационарную точку:
S (a0 , a1 ,..., am )
0, j 0, m.
a j
Перепишем критерий с учетом конкретного вида (x):
n
S(a 0 , a1 ,...,a m ) [a 0 0 ( x i ) a 1 1 ( x i ) ...a m m ( x i ) y i ]2 min
i 0
36
37.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВНайдем частные производные:
n
S(a 0 , a 1 ,..., a m )
2 [a 0 0 ( x i ) ... a m m ( x i ) y i ] 0 ( x i ) 0,
a 0
i 1
n
S(a 0 , a 1 ,..., a m )
2 [a 0 0 ( x i ) ... a m m ( x i ) y i ] 1 ( x i ) 0,
a 1
i 1
.
.
.
.
. .
.
.
.
. .
.
.
.
. .
.
.
.
.
n
S(a 0 , a 1 ,..., a m )
2 [a 0 0 ( x i ) ... a m m ( x i ) y i ] m ( x i ) 0
a m
i 1
Внеся знак суммы ( ) в каждое слагаемое, получим
СЛАУ относительно неизвестных a0, a1, …, am.
37
38.
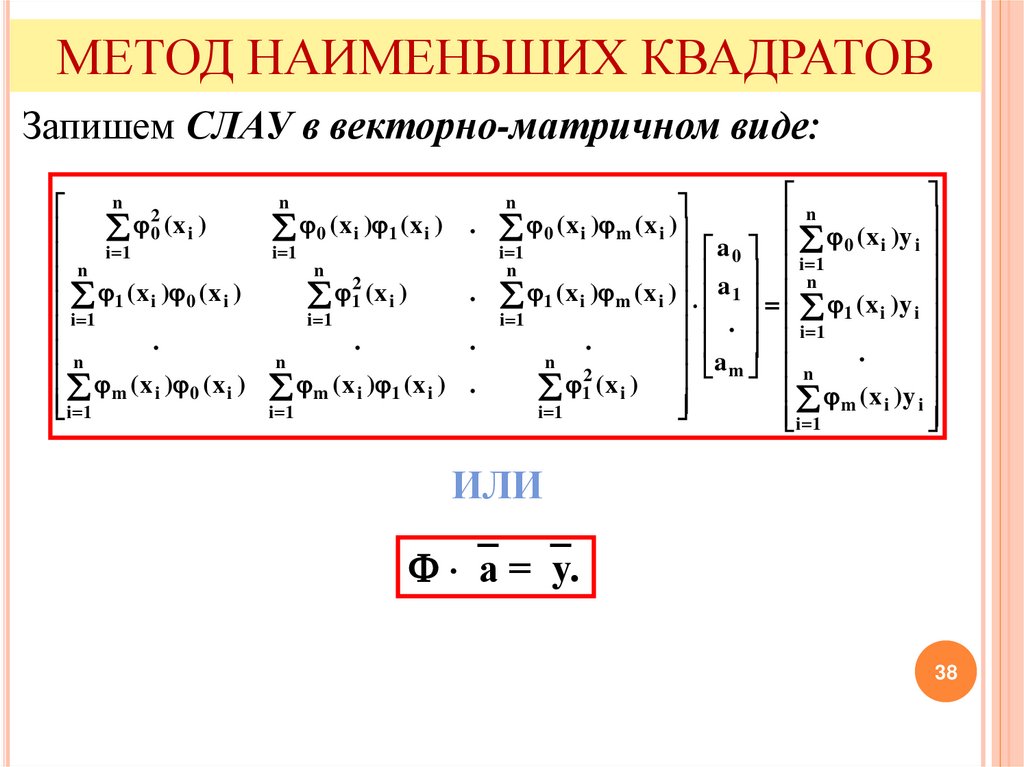
МЕТОД НАИМЕНЬШИХ КВАДРАТОВЗапишем СЛАУ в векторно-матричном виде:
n
02 ( x i )
n i 1
( x ) ( x )
1 i
0
i
i
1
.
n
m ( x i ) 0 ( x i )
i 1
n
0 ( x i ) 1 ( x i )
.
i 1
n
12 ( x i )
.
.
.
m ( x i ) 1 ( x i )
.
i 1
n
i 1
n
0 ( x i ) m ( x i )
(
x
)
y
a 0 i 1 0 i i
i 1
n
a n
1 ( x i ) m ( x i ) 1 1 ( x i )y i
i 1
. i 1
.
.
a
n
m
n
12 ( x i )
m ( x i )y i
i 1
i 1
n
ИЛИ
а = y.
38
39.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВРешение системы единственно и существует, если
определитель матрицы 0.
Это возможно, если в качестве базиса будут выбраны
линейно независимые функции j(x), j=0,m.
ЗАМЕЧАНИЯ:
1. Матрица - матрица Грама:
симметрична относительно главной диагонали.
положительно определенная.
2. МНК эффективен при большом числе измерений n.
39
3. Обязательно n > m. (Иначе имеет место
недоопределенная система).
40.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ4. Если система базисных функций ортогональна, то
есть j(x) i(x), i j, то в матрице Ф ненулевые - только
диагональные элементы. Поэтому решение ее
тривиально.
Пример.
Рассмотрим использование метода МНК для построения
аппроксимирующего уравнения, включающего 2
базисные функции {1, sinx}:
(x)= a0+a1 sin(x).
40
41.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВn
Критерий аппроксимации: S(a 0 , a1 ) [ (x i ) y(x i )]2 min
i 0
Где n – число измерений функции y(x) в узлах xi.
Определение:
Выражение [ ( x i ) y( x i )], определяющее разницу
между исходной и аппроксимирующей функциями,
называется невязками.
Параметры a0, a1 найдем из условия минимума
функции невязок:
S( a 0 , a 1 )
0,
a 0
S( a 0 , a 1 )
0.
a 1
41
42.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВПерепишем критерий с учетом конкретного вида (x):
n
S(a 0 , a 1 ) [a 0 a 1 sin(x i ) y( x i )]2 min
i 0
Найдем частные производные:
n
S( a 0 , a 1 )
2 [a 0 a 1 sin( x i ) y( x i )] 0,
a 0
i 1
n
S( a 0 , a 1 )
2 [a 0 a 1 sin( x i ) y( x i )] sin( x i ) 0.
a 1
i 1
n
n
n
2
a 0 1 a 1 sin( x i ) y( x i ) 1,
i 1
i 1
i 1
n
n
n
a sin( x ) a sin 2 ( x ) y( x ) sin( x ).
i
0
i
1
i
i
i 1
i 1
i 1
42
43.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВПолученные уравнения представляют собой СЛАУ
относительно неизвестных а0, а1:
n
1
i 1
n
sin( xi )
i 1
n
sin(
x
)
y
(
x
)
i
i
a
i 1
i 1
0
.
n
n
a1
2
sin ( xi )
y ( xi ) sin( xi )
i 1
i 1
n
ИЛИ
а = y.
1
a
y
=> вектор искомых коэффициентов:
43
44.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ44
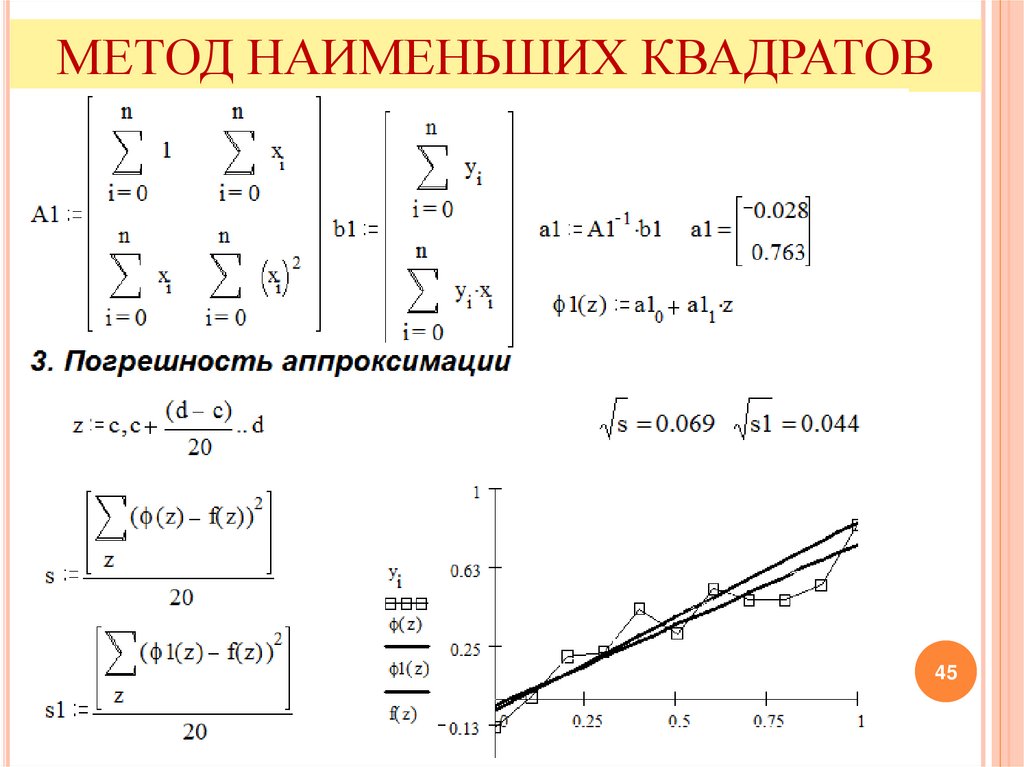
45.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ45
46.
ЭКСТРАПОЛЯЦИЯ ДАННЫХПроцедура predict(y,n,m) позволяет прогнозировать
(экстраполировать) данные на основании имеющихся
табличных значений.
Описание функции
predict(y,n,m)
Аргументы функции
y – векторные значения
функции;
Возвращает
прогнозируемые значения n – глубина предистории;
m – количество
функции.
прогнозируемых значений.
Глубина предистории – это количество последних
значений вектора y {y0, y1, …,yn}, которые
учитываются в прогнозе.
46
47.
ЭКСТРАПОЛЯЦИЯ ДАННЫХПример.
x
x
100
Рассмотрим функцию y( x) e sin( ) , заданную в 100
10
дискретных значениях.
Вектор обозначен {data0, data1, …,data99}.
47
48.
ЭКСТРАПОЛЯЦИЯ ДАННЫХПрогноз осуществляется на 90 значений вперед
пунктирная линия - исходная функция.
48
49.
ЭКСТРАПОЛЯЦИЯ ДАННЫХЗАМЕЧАНИЯ:
1. Экспериментальных данных должно быть достаточно
(>>10).
2. В прогнозе (предистории) должна участвовать только
часть экспериментальных данных.
3. Эффективен только краткосрочный прогноз.
4. Расхождение с истинными значениями заданной
функции особенно заметно в последних точках
прогнозируемых данных.
5. Шаг прогноза необходимо выбирать как в
экспериментальных данных.
49
50.
ЭФФЕКТИВНОСТЬ АППРОКСИМАЦИИОценка эффективности аппроксимации:
качественные показатели,
количественные показатели.
Качественная оценка проводится путем визуального
оценивания графиков истинной и аппроксимирующей
функций (субъективная оценка).
Для количественной оценки вводят показатели
точности аппроксимации.
50
51.
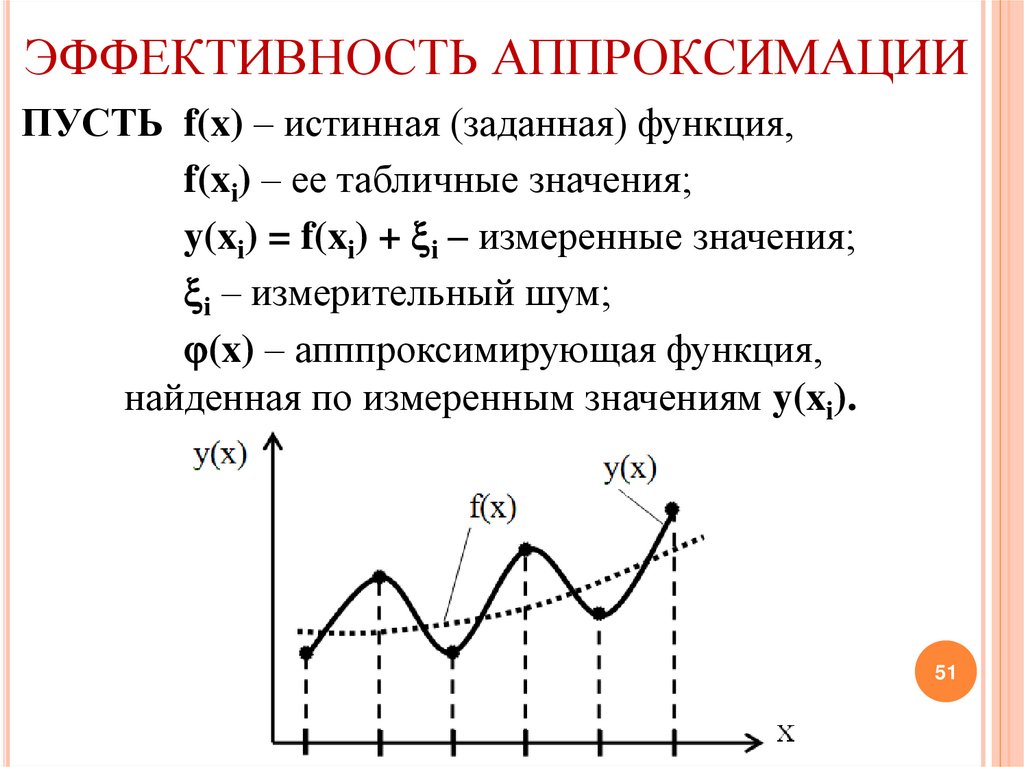
ЭФФЕКТИВНОСТЬ АППРОКСИМАЦИИПУСТЬ f(x) – истинная (заданная) функция,
f(xi) – ее табличные значения;
y(xi) = f(xi) + i – измеренные значения;
i – измерительный шум;
(x) – апппроксимирующая функция,
найденная по измеренным значениям y(xi).
51
52.
ЭФФЕКТИВНОСТЬ АППРОКСИМАЦИИПоказатели эффективности аппроксимации:
Среднеквадратическая погрешность:
1 n
[ ( xi ) f ( xi )]
n i 0
2
Максимальная погрешность:
max ( x i ) f ( x i )
i
Приведенная среднеквадратическая погрешность:
f max f min
100
52












































 Математика
Математика








