1. радианная мера угла

1.

Тригонометрия

2.

Немного из истории…
1. Древние вавилоняне и египтяне изучали тригонометрию как часть астрономии; разделили окружность на 360
2. Древние индийцы: ввели названия
«синус», «косинус», составили таблицы
синусов, косинусов
3. IX-XVвв – Средний и Ближний
восток: составляли таблицы котангенса, тангенса, косеканса; ввели
понятие единичной окружности

3.

Немного из истории…
4. Насир ад-Дин Мухаммад ат-Туси
(1201-1274) выделил раздел
тригонометрии из астрономии
5. Лев Герсонид (1288-1344) – открыл
теорему синусов
6. XVII-XIXвв: применение тригонометрии в механике, физике, технике, как
часть математического анализа (Виетт,
Бернулли) – тригонометрические
символы, графики – синусоиды
7. Л.Эйлер: придал тригонометрии
современный вид

4.

Тригонометрия
(«три» - три, «гониа» - угол,
«метриа» - измеряю)
раздел математики,
изучающий
соотношение сторон и
углов в треугольнике

5.

Какой угол в окружности
называют центральным?
Это плоский угол
с вершиной в
центре
окружности
В
А

6.

Что такое дуга окружности?
Это часть
окружности,
расположенной
внутри плоского
угла.

7.

Градусная мера дуги окружности
это градусная мера
соответствующего
центрального угла.

8.

Единицы
измерения углов
Градусы
Радианы

9.

Градусная мера угла
=1
1 – цена одного деления
окружности, разделенной на
360 частей

10.

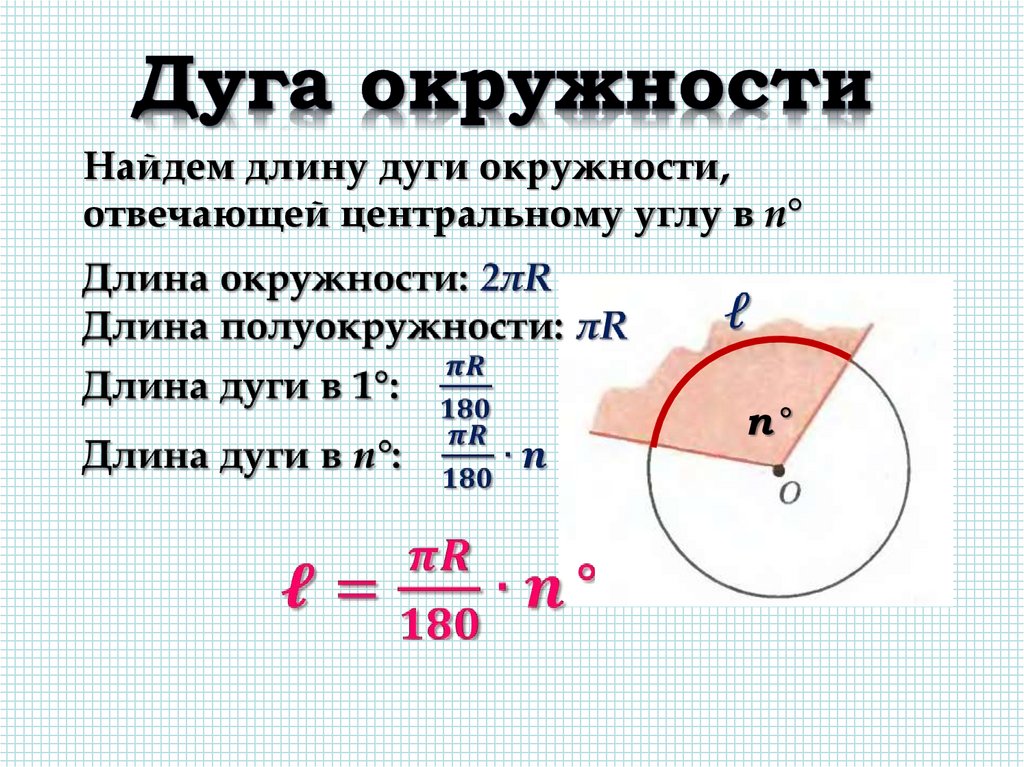
Найдем длину дуги окружности,
отвечающей центральному углу в n°
n°

11.

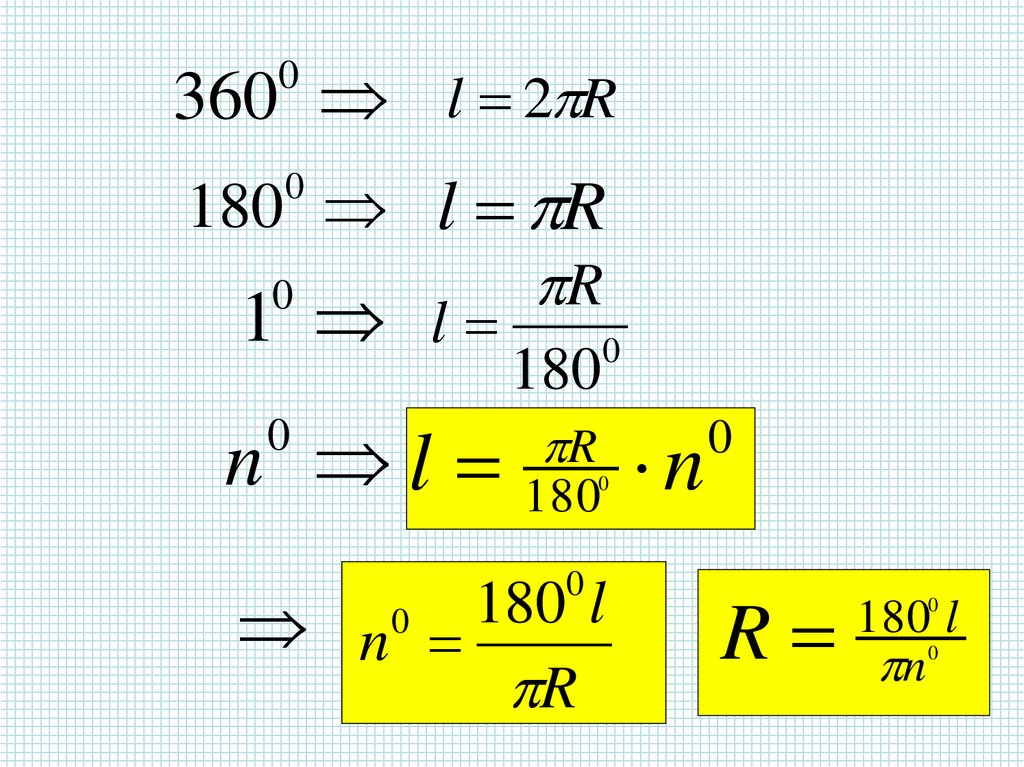
360 l 2 R
0
180 l R
R
0
0
1 l
180
0
n l 180 n
0
R
0
0
0
180
l
0
n
R
R
0
180 l
0
n

12.

Радианная мера угла
Радиан – отношение длины
дуги, стягивающей угол, к
радиусу окружности.
l
R
0
0
n
n
0
0
R 180 R
180

13.

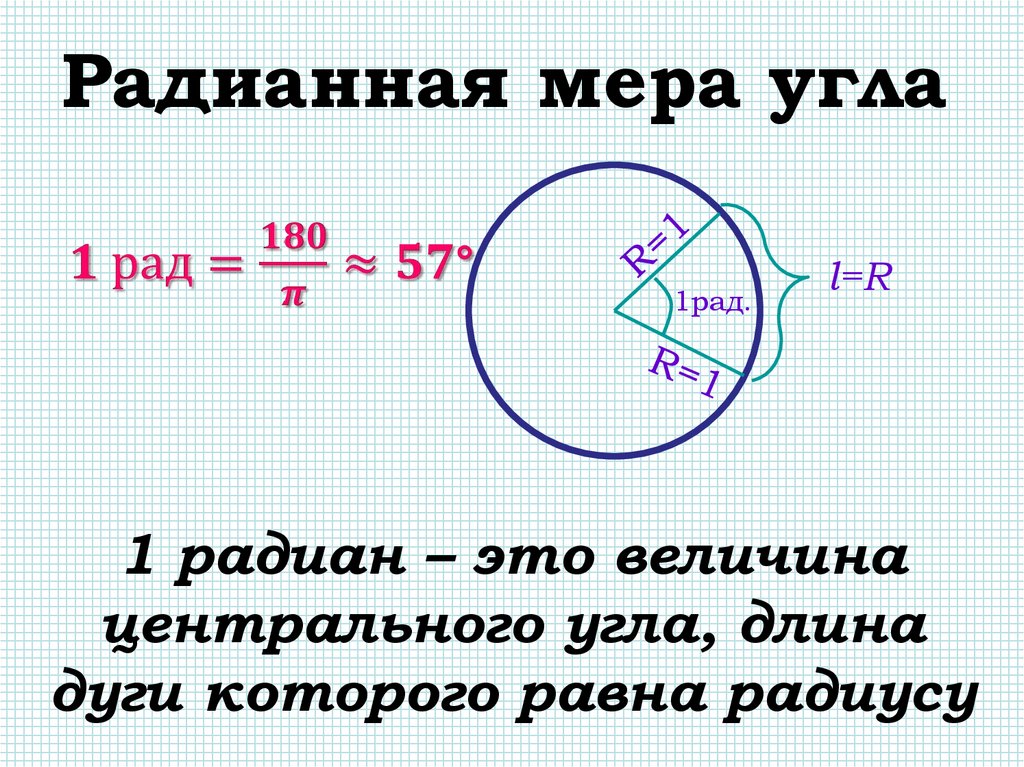
Радианная мера угла
1рад.
l=R
1 радиан – это величина
центрального угла, длина
дуги которого равна радиусу

14.

Радианная мера угла
l= R
Длина дуги окружности в
радиан: l= R

15.

Найти длину дуги окружности
радиуса 6 см, если градусная мера
соответствующего центрального
угла 30°

16.

Связь между градусной и
радианной мерами угла
.
Длина окружности:
.
Радианная мера:
С 2 R
С
2 R
2
R
R
2 360
180

17.

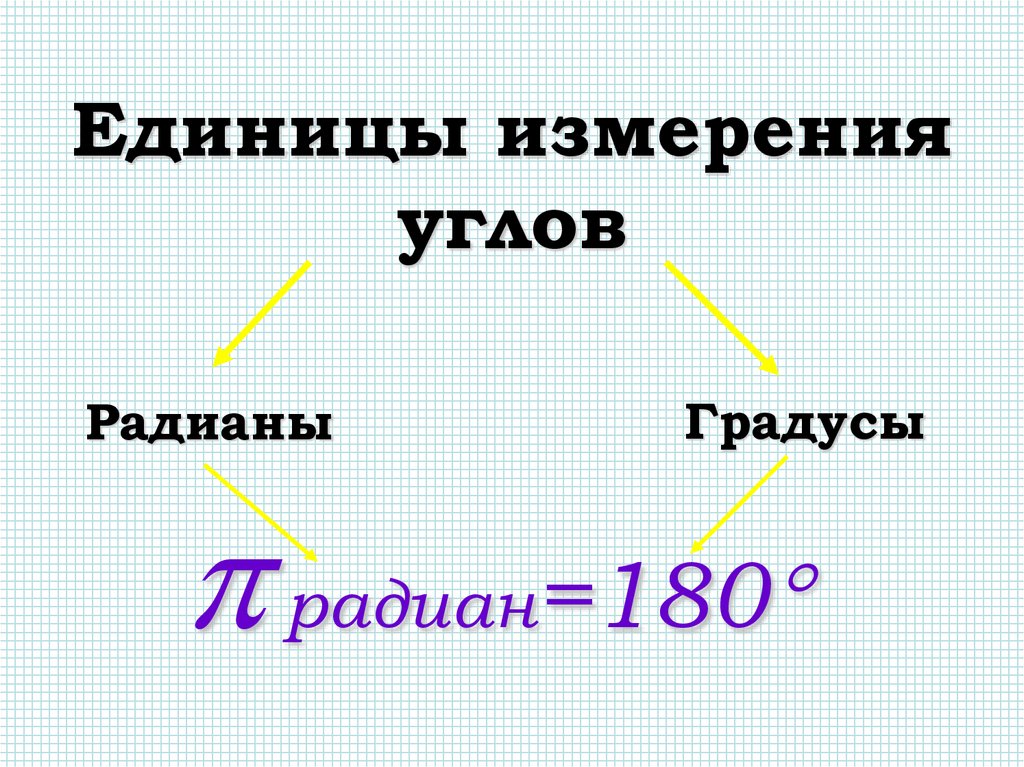
Единицы измерения
углов
Радианы
Градусы
радиан=180

18.

Перевод из градусной меры в
радианную:
pадиан = 180
радиан = n
180
n
0
n ( рад.)
180

19.

0
n
(
рад
.)
180
Пример 2:
n 135
135 3
135
180
180
4

20.

Пример:
1. 30
30
рад.
рад.
6
180
90
рад
.
рад.
2. 90
180
2
3
135
рад
.
рад
.
3.135
4
180

21.

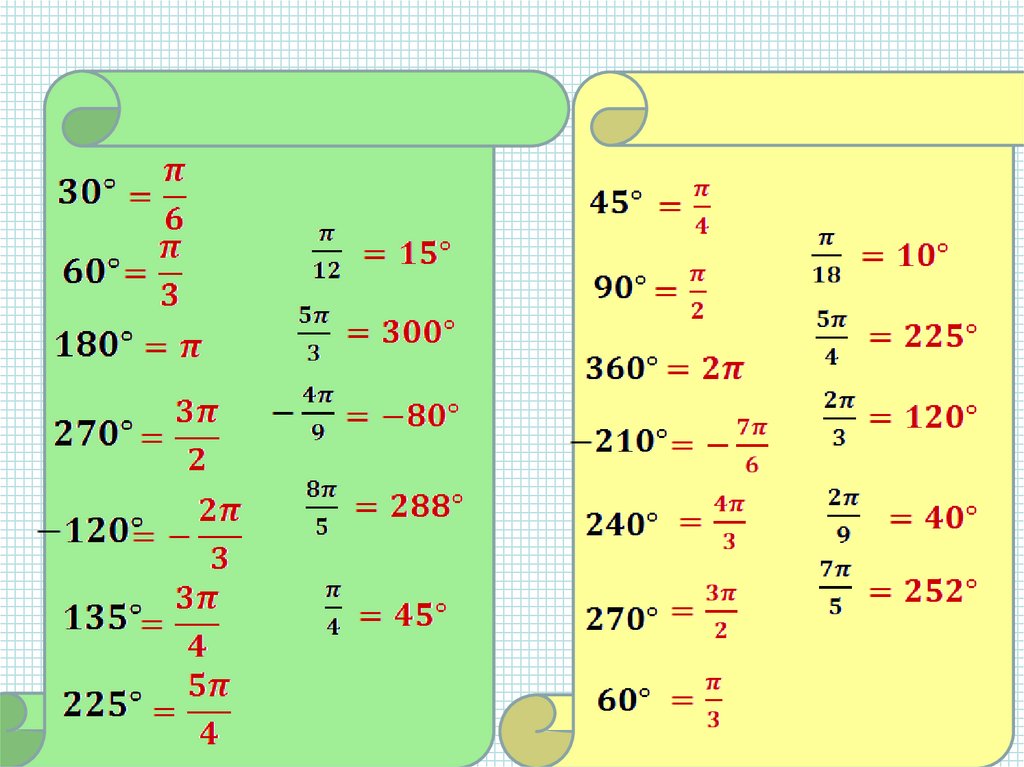
Переведите в радианную
меру углы:
1) 45
2) 15
3) 72

22.

Пример:
1. 45
45
рад.
рад.
4
180
15
рад
.
рад.
2. 15
180
12
2
72
рад
.
рад
.
3. 72
5
180

23.

Перевод из радианной меры в градусную:
Радиан = 180
радиан = n
n
180
0

24.

Пример:
180
1.
60
рад.
3
3
180
2.
30
рад.
6
6
4 180
4
3.
240
рад.
3
3

25.

Переведите в градусную
меру углы:
1)
рад.
9
2)
рад.
5
5
3)
рад.
12

26.

Пример:
180
1.
рад.
20
9
9
180
2.
36
рад.
5
5
4 180
4
3.
рад.
144
5
5

27.

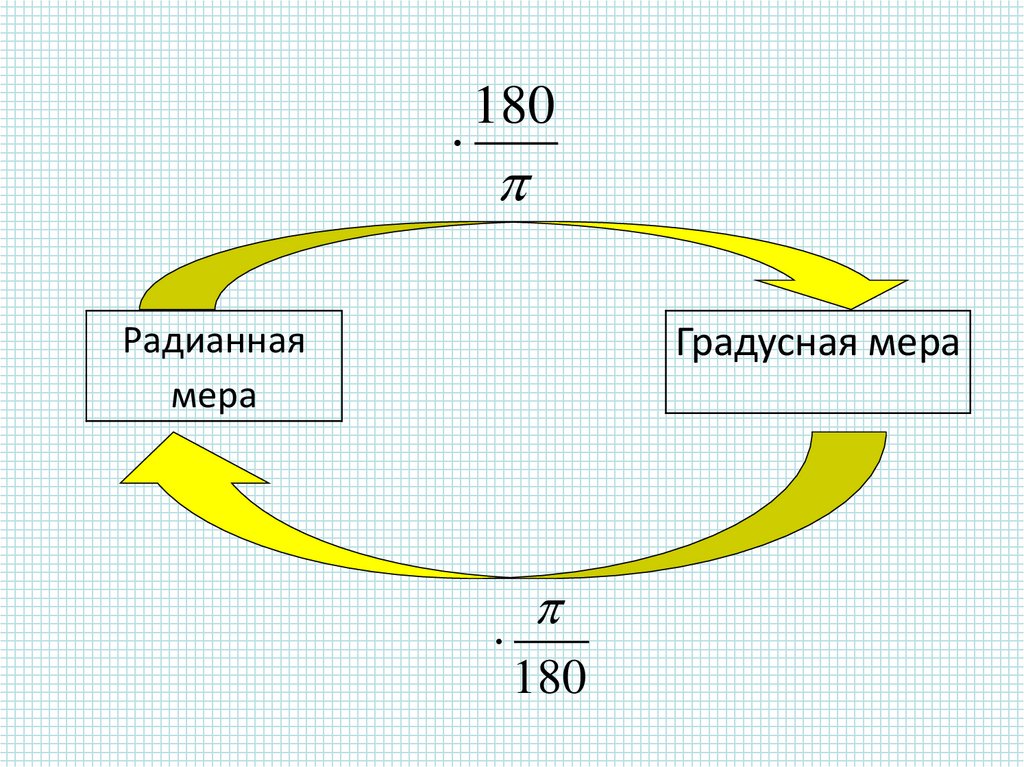
180
Радианная
мера
Градусная мера
180