Похожие презентации:
Подготовка к экзамену по дисциплине -1-
1. Подготовка к экзамену по дисциплине «Основы криптографии» (бакалавриат)
Кафедра «Информационной безопасности»к.т.н., доцент Волгина Людмила Всеволодовна
LVVolgina@fa.ru
2.
Объявление результатов 19.01.2026 15-00 аудитория 23163.
Объявление результатов 21.01.2026 15-00 аудитория 23264.
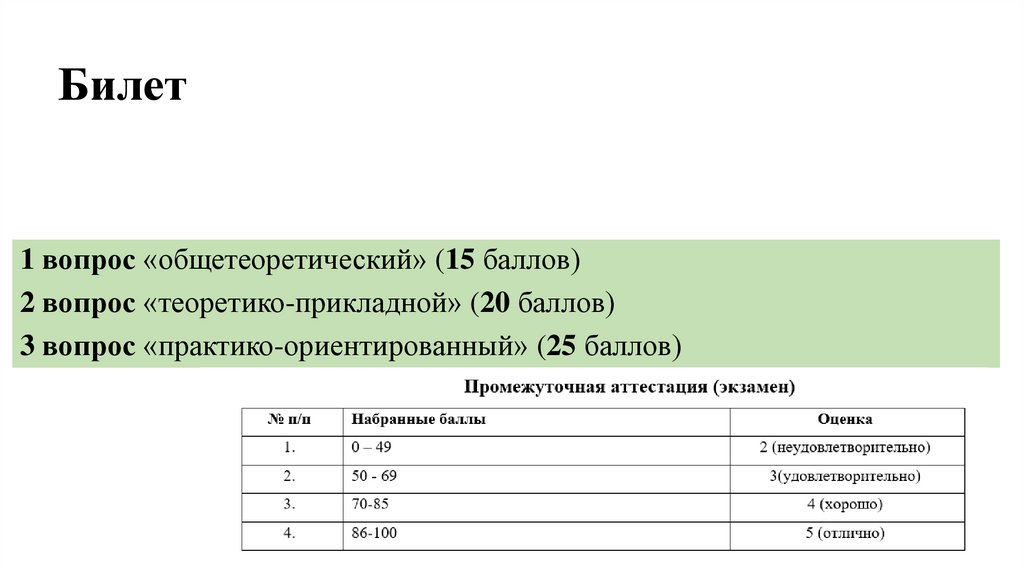
Объявление результатов 21.01.2026 16-00 аудитория 23265. Билет
1 вопрос «общетеоретический» (15 баллов)2 вопрос «теоретико-прикладной» (20 баллов)
3 вопрос «практико-ориентированный» (25 баллов)
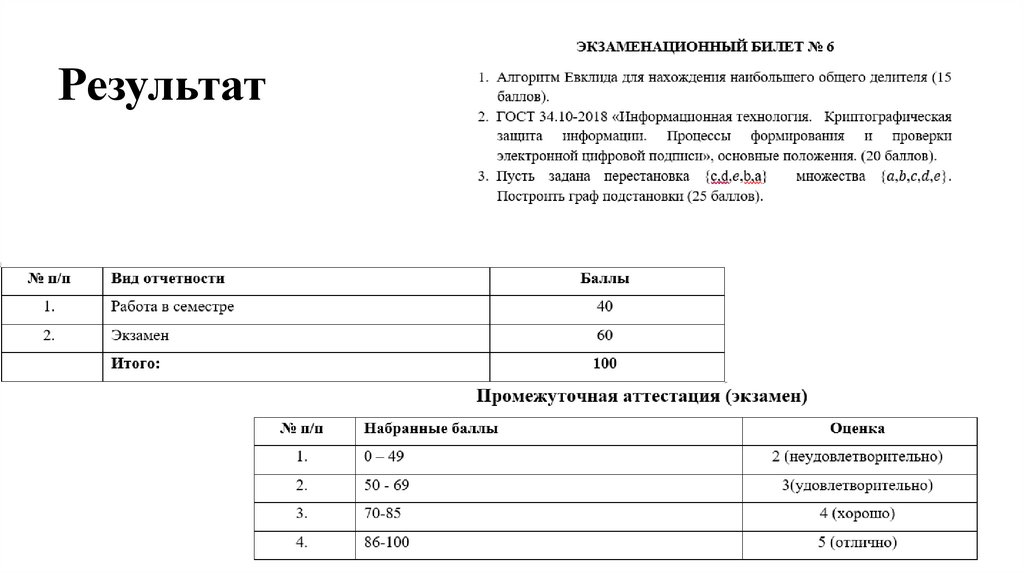
6. Результат
7. 1 вопрос – рекомендации к получению 15 баллов
1). Внимательно прочесть вопрос.2). Дать определение, указать свойства, привести примеры.
3). Указать как применяется в криптографии.
8. 2 вопрос – рекомендации к получению 20 баллов
1). Внимательно прочесть вопрос.2). Дать определение, указать алгоритм, схему или формулу с
расшифровкой всех элементов.
3). Ответить на вопрос максимально подробно и записать ответ
9. 3 вопрос – рекомендации к получению 25 баллов
1). Внимательно прочесть вопрос.2). Представить вычисления, показать расчетный
алгоритм
Если нет 2 и не верно 3 – 0б
3). Записать ответ.
Если нет 2, но есть 3 и верно 5б
Если верно 2, но 3 не верно, 15-20б
(в зависимости от грубости ошибки)
10. Пишите, пожалуйста разборчиво
11. Как ответить на вопросы: (вопросы от студентов)
Как ответить на вопросы: (вопросы от студентов)Краткие сведения из истории криптографии.
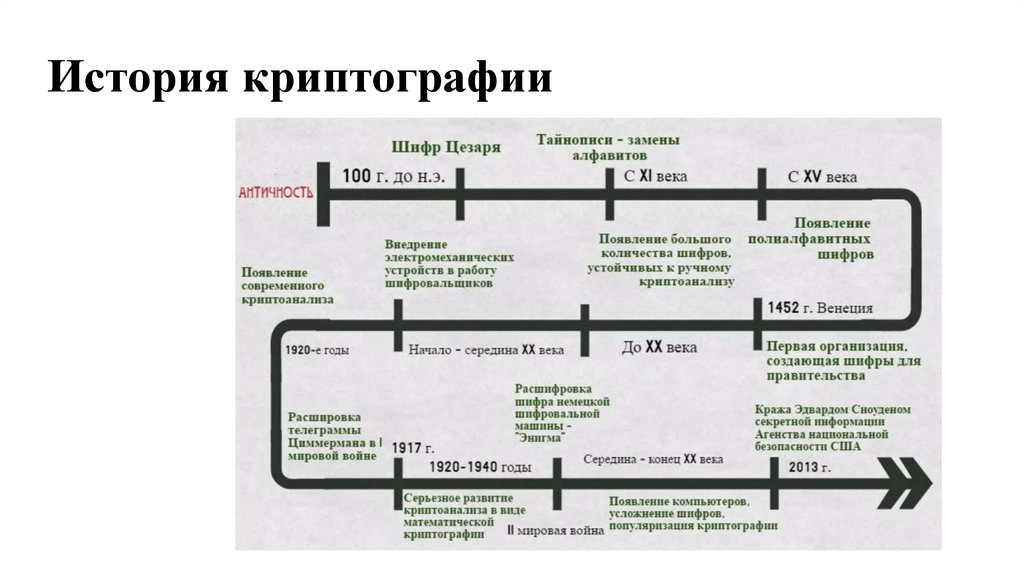
12. История криптографии
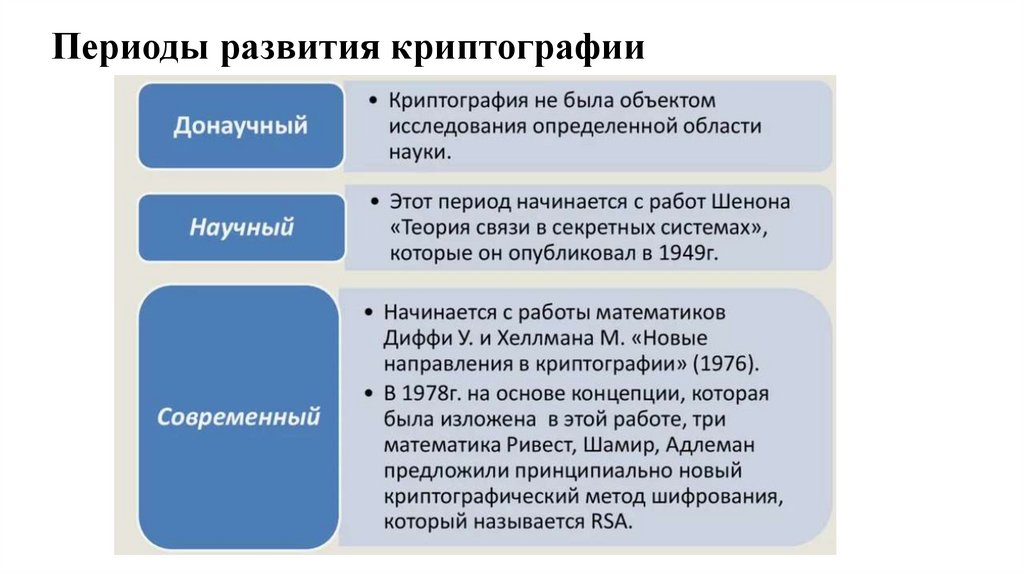
13. Периоды развития криптографии
14.
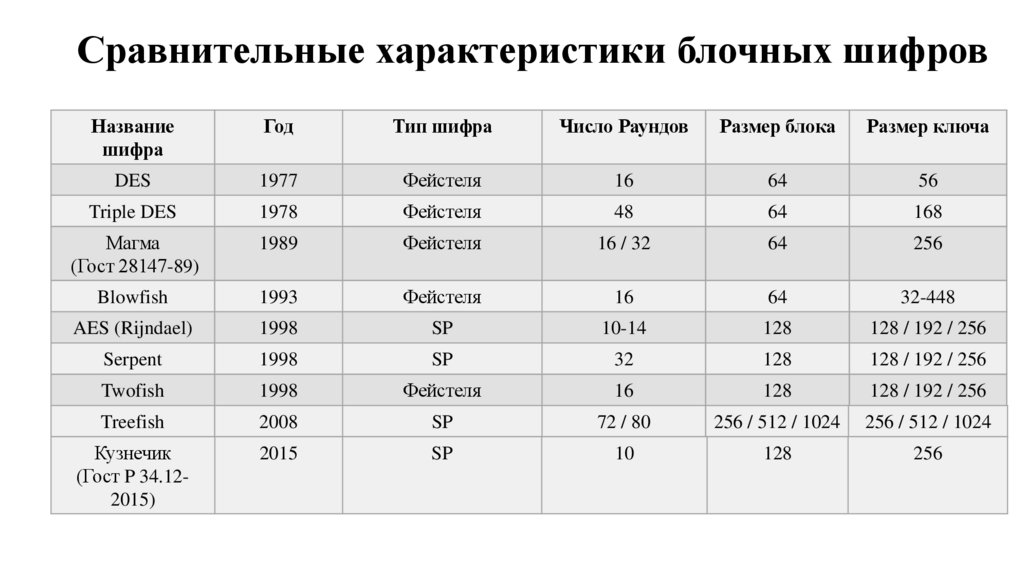
Основные события в XX в• переход от ручных шифров к машинным, а затем и электронным
шифрам;
• разработку блочных и двухключевых систем для защиты компьютерной
информации;
• использование физических принципов (электронных, квантовых);
• бурное развитие криптологии и смежных наук;
• разработку новых технологий вычислений с использованием
информационно-телекоммуникационных сетей (квантовых, кластерных,
распределенных вычислений).
15. Как ответить на вопросы: (вопросы от студентов)
Как ответить на вопросы: (вопросы от студентов)«Арифметика остатков. Группы и кольца»: определения «арифметика остатков», «группа», «кольцо»;
Опр. Арифметика – раздел математики, изучающий числа, их отношения и свойства.
Числа бывают….(дополнительная информация)
Остаток от деления = кольцо вычетов (важно!)
16.
Указать как применяется в криптографии:Остаток от деления
Кольцо вычетов
Сравнение по модулю
Алгоритм RSA
17. Как ответить на вопросы: (вопросы от студентов)
Как ответить на вопросы: (вопросы от студентов)Основы вычислений в конечных полях
Арифметика в конечном поле — это арифметика в
поле, содержащем конечное число элементов. Она
противоположна арифметике в поле с бесконечным
числом элементов, например, в поле рациональных
чисел.
Поле Галуа — это математическое понятие в
абстрактной алгебре, которое имеет дело с
конечными математическими структурами.
Это набор чисел, состоящий из конечного числа
элементов и состоящий из двух операций —
сложения и умножения, которые выполняются по
определённым правилам.
18.
Конечное поле GF(q) – поле Галуа, q – порядок поля (количествоэлементов).
Любое простое число можно составить как множество остатков от деления
натуральных чисел на p (0,1,…p-1) c операциями сложения и умножения по
модулю p. Примеры таблиц сложения и умножения в полях
GF(2),GF(3),GF*5)
19.
Проверка чисел на простоту:1). Проверить делится ли на все простые числа в рассматриваемом
диапазоне (метод пробных делений)
2). Использовать решето Эрастофена
3). Использовать китайскую теорему об остатках
4). Использовать теорему Ферма
20. Как ответить на вопросы: (вопросы от студентов)
Как ответить на вопросы: (вопросы от студентов)Требования к системам шифрования и примеры их реализации в
классических криптографических алгоритмах.
21.
Фундаментальный труд К. ШеннонаИсследование абсолютно секретных систем
(доказательство их существования)
Существование криптостойких шифров (требуемые
для этого условия)
Сформулировал основные требования, предъявляемые к
надежным шифрам (абсолютно стойкие шифры).
Методы создания криптостойких систем шифрования на
основе простых операций.
Создал математическую модель системы связи
Он ввел понятия:
Бит, энтропия, рассеивание и перемешивание
Клод Шеннон
(30.04.1916 — 24.02.2001)
американский учёный и инженер,
иностранный член Нидерландской
королевской академии наук (1975)
В 1948 году в результате восьми лет размышлений стала статья «Математическая теория связи» («Теория связи в
секретных системах»). 77 страниц, 23 теоремы и семь приложений с доказательствами навсегда изменили мир и вписали
имя К. Шеннона в историю.
22.
Абсолютно стойкие системыОпр. Абсолютная стойкость (или теоретическая стойкость) криптосистемы, это система, которая не
может быть раскрыта ни теоретически, ни практически даже при наличии у атакующего бесконечно больших
вычислительных ресурсов.
Доказательство существования абсолютно стойких алгоритмов шифрования было выполнено К.Шенноном и
опубликовано в работе «Теория связи в секретных системах».
Там же определены требования к такого рода системам:
• ключ генерируется для каждого сообщения (каждый ключ используется только один раз)
• ключ статистически надёжен (то есть вероятности появления каждого из возможных символов равны,
символы в ключевой последовательности независимы и случайны)
• длина ключа равна или больше длины сообщения
• исходный (открытый) текст обладает некоторой избыточностью (что является критерием оценки
правильности расшифровки)
23.
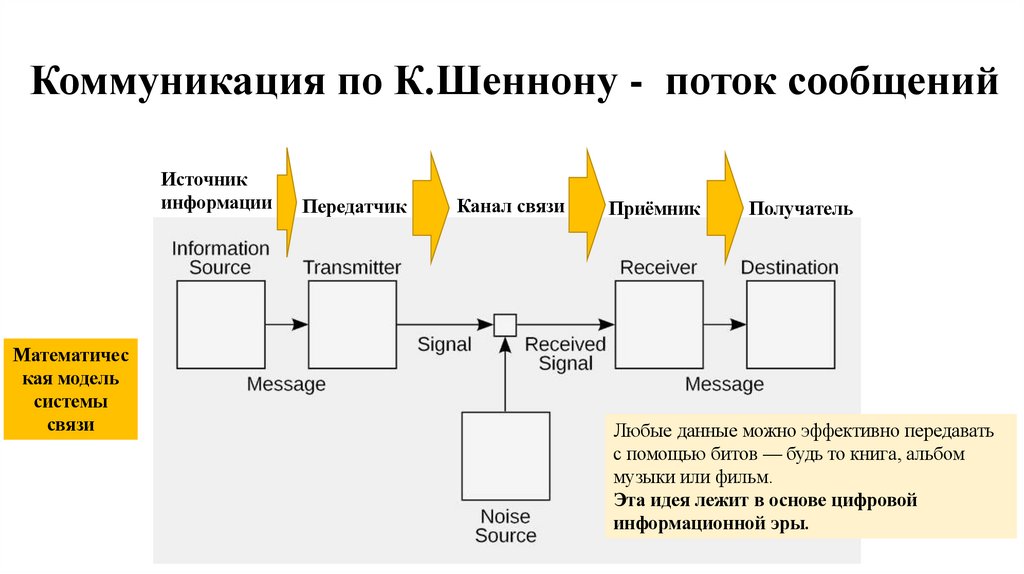
Коммуникация по К.Шеннону - поток сообщенийИсточник
информации
Математичес
кая модель
системы
связи
Передатчик
Канал связи
Приёмник
Получатель
Любые данные можно эффективно передавать
с помощью битов — будь то книга, альбом
музыки или фильм.
Эта идея лежит в основе цифровой
информационной эры.
24. Как ответить на вопросы: (вопросы от студентов)
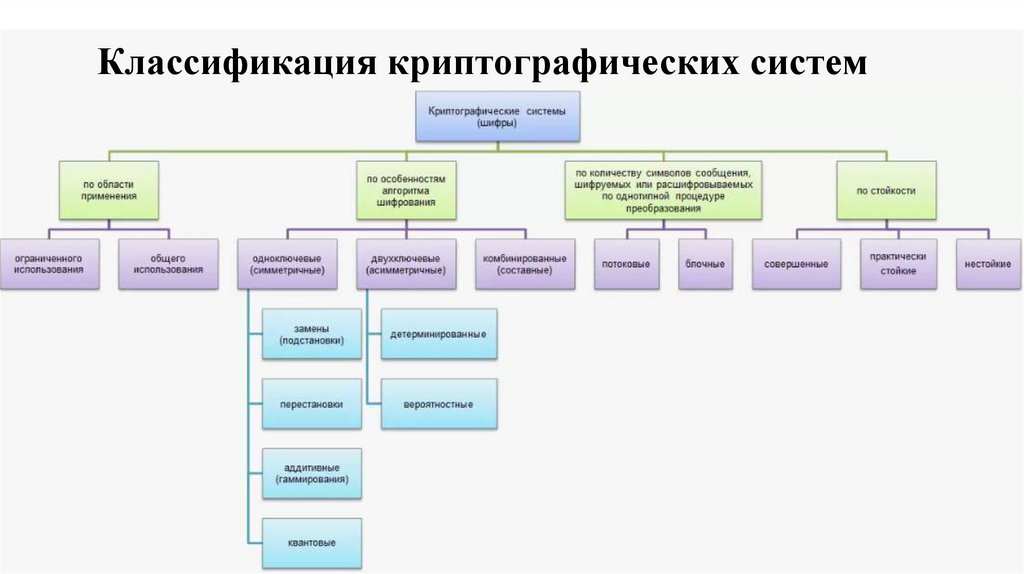
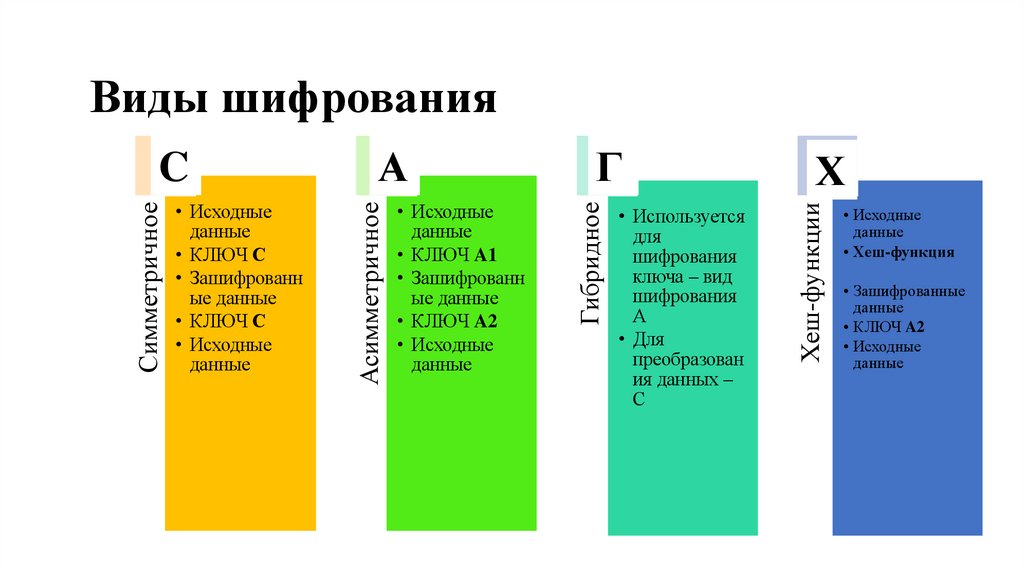
Как ответить на вопросы: (вопросы от студентов)Классификация классических криптоалгоритмов, примеры реализации
моноалфавитных, многоалфавитных подстановок и шифров перестановок.
25.
Математическая модель шифраОбозначения:
X – конечное множество возможных открытых текстов
K – конечное множество возможных ключей
Y – конечное множество возможных зашифрованных текстов