Похожие презентации:
3 лекция увел рисунки
1.
ВОЛНЫВИДЫ ВОЛН.
УРАВНЕНИЯ ПЛОСКОЙ И СФЕРИЧЕСКОЙ ВОЛН.
Волна - процесс распространения колебаний в пространстве.
Виды волн:
- продольные;
- поперечные.
2.
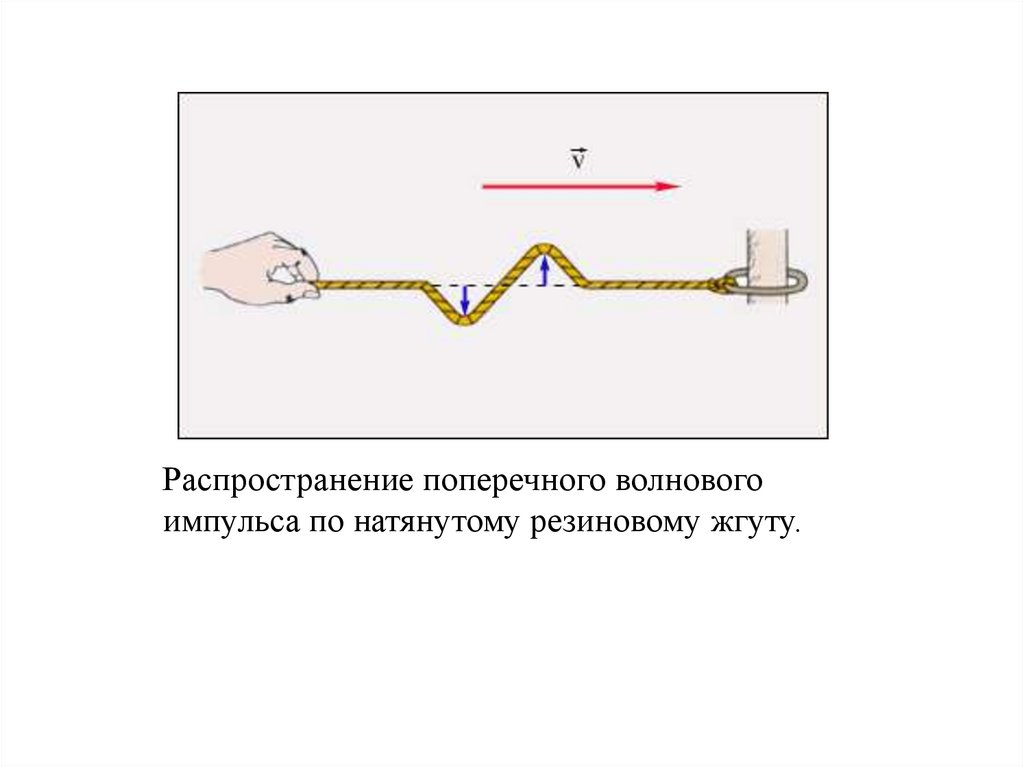
Распространение поперечного волновогоимпульса по натянутому резиновому жгуту.
3.
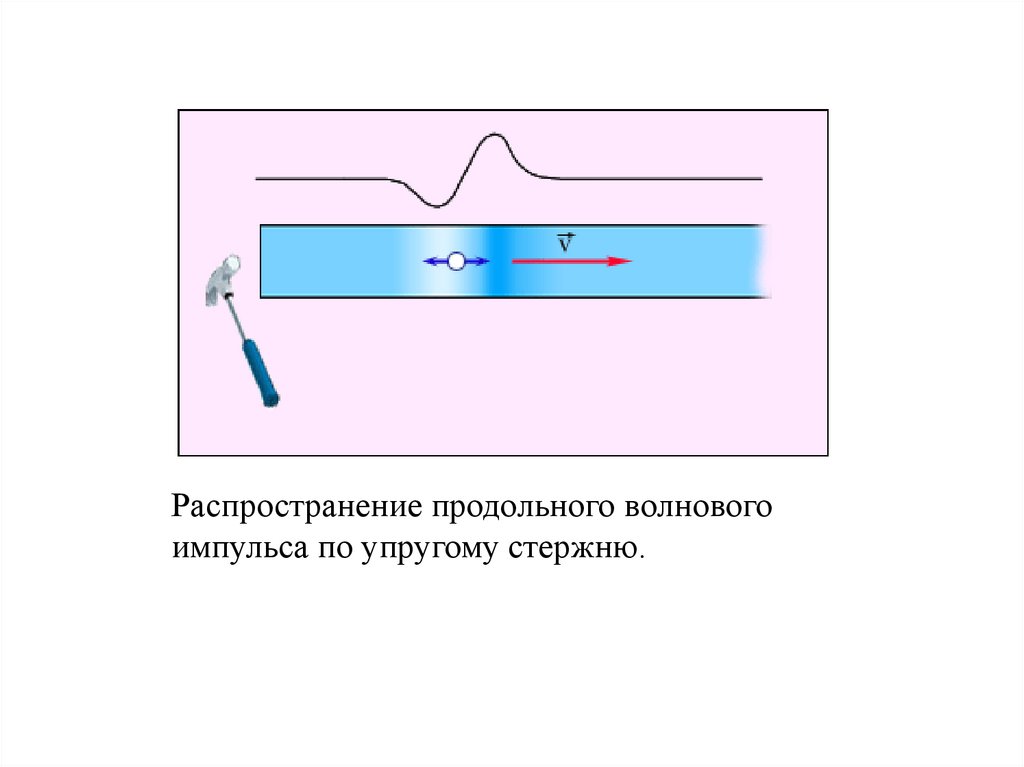
Распространение продольного волновогоимпульса по упругому стержню.
4.
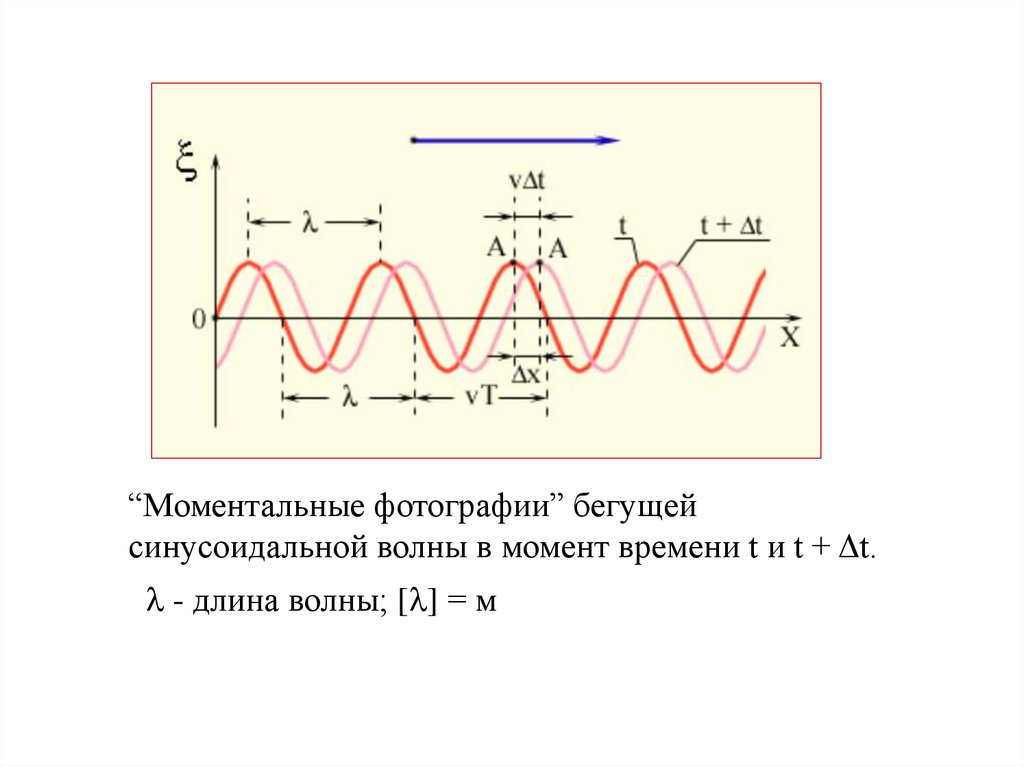
“Моментальные фотографии” бегущейсинусоидальной волны в момент времени t и t + Δt.
- длина волны; [ ] = м
5.
T1
T
:
С учетом
Фронт волны:
геометрическое место точек, до которых дошли колебания
в данный момент времени.
Волновая поверхность:
геометрическое место точек, колеблющихся в одинаковой
фазе. (волны: плоские, сферические и др.)
6.
( x, y, z, t ) - уравнение волныРассмотрим плоскую волну, распространяющуюся в
направлении оси Х:
7.
( x 0, t ) A cos( t )( x, t ) A cos[ ( t ) ]
x
x
( x, t ) A cos[ ( t ) ]
- фазовая скорость, т.е. скорость с которой
перемещается данное значение фазы.
При фиксированной фазе:
dx
dt
8.
x( x, t ) A cos[ t ]
2
k
- волновое число
A cos[ t kx ]
k
2 2
- незатухающая волна
A 0 e x cos[ t kx ]
- затухающая волна
(в поглощающей среде)
9.
Рассмотрим сферическую волнуФаза волны для точек, лежащих на волновой
поверхности радиуса r:
r
[ ( t ) ] t kr
Уравнение сферической волны в непоглощающей среде:
A
cos( t kr )
r
Уравнение сферической волны в поглощающей среде:
A r
e cos( t kr )
r
10.
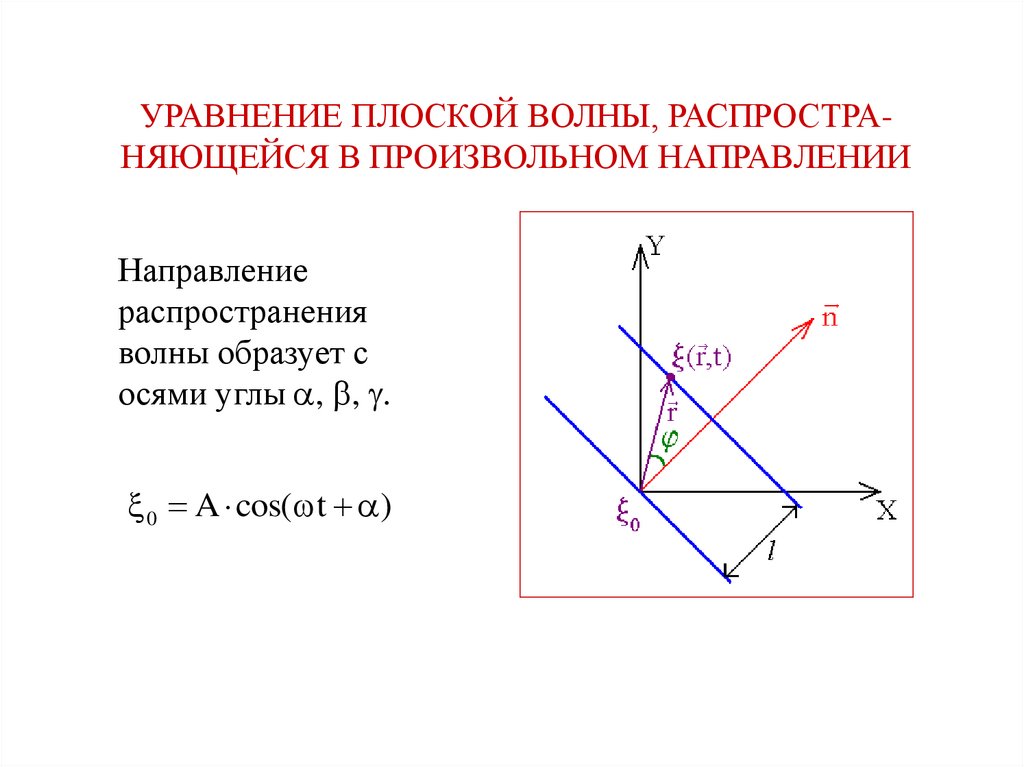
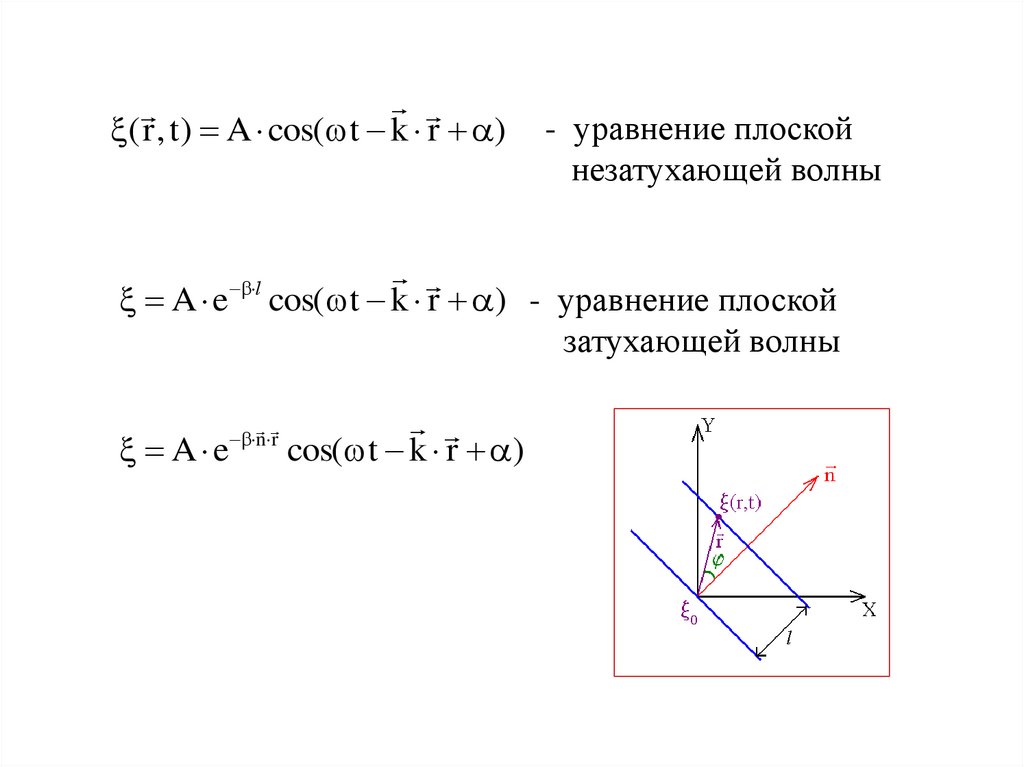
УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ, РАСПРОСТРАНЯЮЩЕЙСЯ В ПРОИЗВОЛЬНОМ НАПРАВЛЕНИИНаправление
распространения
волны образует с
осями углы , , .
0 A cos( t )
11.
12.
Бегущими волнами называются волны, которые переносят в пространствеэнергию. Перенос энергии волнами количественно характеризуется
вектором плотности потока энергии. Этот вектор для упругих волн
называется вектором Умова (пэнергии, а его модуль равен энергии,
переносимой волной за единицу времени через единичную площадку,
расположенную перпендикулярно направлению распространения волны.о
имени русского ученого Н. А. Умова (1846—1915), решившего задачу о
распространении энергии в среде). Направление вектора Умова совпадает с
направлением переноса
13.
lA cos( ( t ) )
A cos( t k l )
Для произвольной точки волновой поверхности:
n r 1 r cos l
A cos( t k n r )
k k n - волновой вектор
2
k k
14.
( r , t ) A cos( t k r )- уравнение плоской
незатухающей волны
cos( t k r ) - уравнение плоской
затухающей волны
A e
l
A e
n r
cos( t k r )
15.
Перепишем через координаты уравнение:( r , t ) A cos( t k r )
k r k (x i y j z k)
k x i k y j k z k
k x 1 cos k y 1 cos k z 1 cos
kx x k y y kz z
16.
( x, y, z, t ) A cos( t k x x k y y k z z )2
k x cos
2
k y cos
2
k z cos
17.
ВОЛНОВОЕ УРАВНЕНИЕУравнение волны является решением волнового уравнения.
Получим волновое уравнение.
( r , t ) A cos( t k r )
( x, y, z, t ) A cos( t k x x k y y k z z )
(
A
sin(
t
k
r
)
)
2
t
t
2
2
A cos( t k r )
2
18.
( r , t ) A cos( t k r )( x , y, z, t ) A cos( t k x x k y y k z z )
2
(A sin( t k r ) k x )
2
x
x
2
2
k x A cos( t k r ) k x
2
(A sin( t k r ) k y )
2
y
y
2
2
k y A cos( t k r ) k y
2
( A sin( t k r ) k z )
2
z
z
2
2
k z A cos( t k r ) k z
19.
22
2
2
2 2 ( k x k y k z ) k
2
x y z
2
2
2
2
2
t
2
1
2 2
t
2
2
2
2
2
2
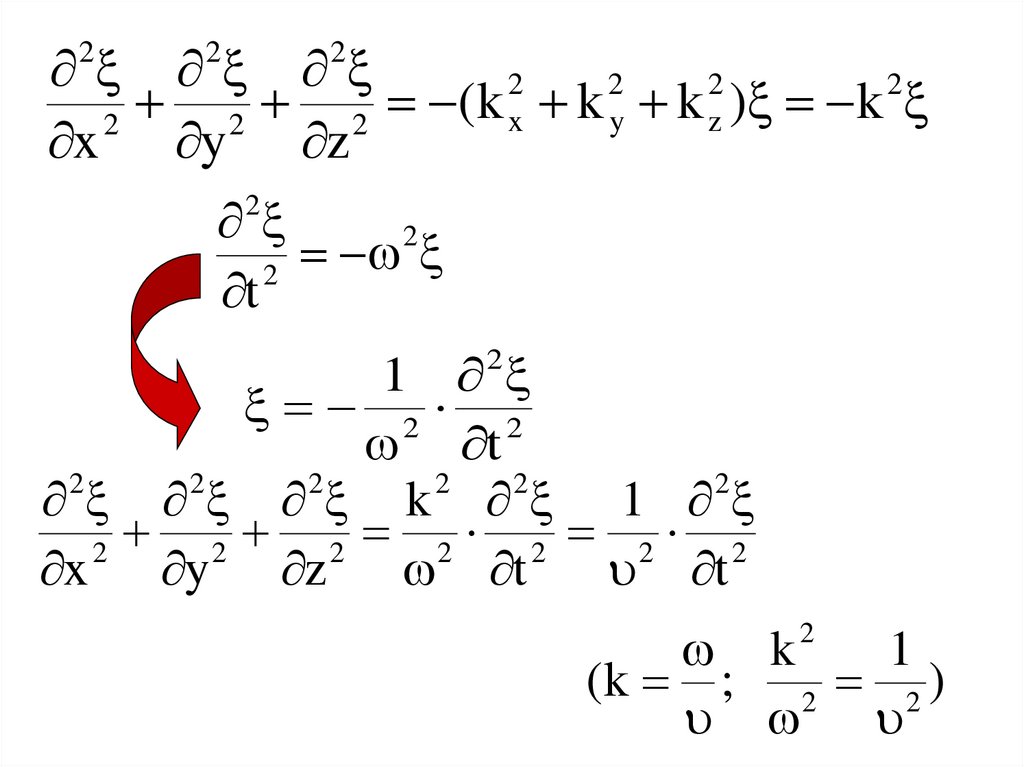
k 1
2 2 2 2 2 2
2
x y z
t
t
2
k
1
(k ; 2 2 )
2
20.
12
2
2
2
2
x y z
t
2
2
2
1
2 2
t
2
2
2 2 2
x y z
2
2
Для плоской волны, распространяющейся в направлении х:
2 1 2
2 2
2
x t
2
21.
Принцип суперпозиции. Групповая скоростьЕсли среда, в которой распространяется одновременно несколько
волн, линейна, т. е. ее свойства не изменяются под действием
возмущений, создаваемых волной, то к ним применим принцип
суперпозиции (наложения) волн: при распространении в
линейной среде нескольких волн каждая из них распространяется
так, как будто другие волны отсутствуют, а результирующее
смещение частицы среды в любой момент времени равно
геометрической сумме смещений, которые получают частицы,
участвуя в каждом из слагающих волновых процессов.
Исходя из принципа суперпозиции и разложения Фурье (см.
(144.5)) любая волна может быть представлена в виде суммы
гармонических волн, т. е. в виде волнового пакета, или группы
волн. Волновым пакетом называется суперпозиция волн, мало
отличающихся друг от друга по частоте, занимающая в каждый
момент времени ограниченную область пространства.
22.
23.
«Сконструируем» простейший волновой пакетиз двух распространяющихся вдоль
положительного направления оси х
гармонических волн с одинаковыми
амплитудами, близкими частотами и волновыми
числами, причем d << и dk<<k. Тогда
24.
есть медленно изменяющаяся функция координаты х и времени t.За скорость распространения этой негармонической волны (волнового
пакета) принимают скорость перемещения максимума амплитуды волны,
рассматривая тем самым максимум в качестве центра волнового пакета.
При условии, что td —xdk = const, получим
Скорость и есть групповая скорость. Ее можно определить как
скорость движения группы волн, образующих в каждый момент
времени локализованный в пространстве волновой пакет.
Выражение (155.1) получено для волнового пакета из двух
составляющих, однако можно доказать, что оно справедливо в
самом общем случае.
25.
26.
27.
Из формулы вытекает, что u может быть как меньше, так и больше v взависимости от знака dv/d . В недиспергирующей среде dv/d =0 и
групповая скорость совпадает с фазовой.
Понятие групповой скорости очень важно, так как именно она
фигурирует при измерении дальности в радиолокации, в системах
управления космическими объектами и т. д. В теории относительности
доказывается, что групповая скорость u<<с, в то время как для фазовой
скорости ограничений не существует.
28.
Интерференция волнСогласованное протекание во времени и пространстве нескольких
колебательных или волновых процессов связывают с понятием
когерентности. Волны называются когерентными, если разность их
фаз остается постоянной во времени. Очевидно, что когерентными
могут быть лишь волны, имеющие одинаковую частоту. При наложении
в пространстве двух (или нескольких) когерентных волн в разных его
точках получается усиление или ослабление результирующей волны в
зависимости от соотношения между фазами этих воли. Это явление
называется интерференцией волн.
29.
E - фазовая скорость продольной волныЕ - модуль Юнга
G - фазовая скорость поперечной волны
G - модуль сдвига
30.
31.
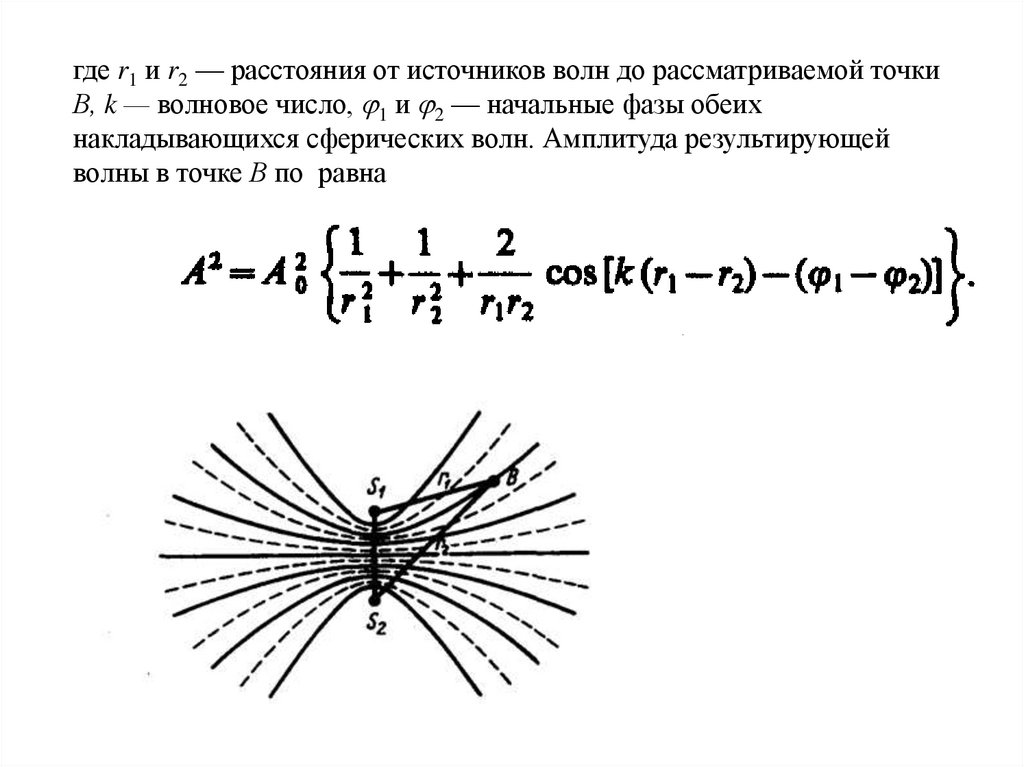
где r1 и r2 — расстояния от источников волн до рассматриваемой точкиВ, k — волновое число, 1 и 2 — начальные фазы обеих
накладывающихся сферических волн. Амплитуда результирующей
волны в точке В по равна
32.
33.
Так как для когерентных источников разность начальных фаз ( 1 – 2) =const, то результат наложения двух волн в различных точках зависит от
величины = r1 – r2, называемой разностью хода волн.
В точках, где
наблюдается интерференционный максимум: амплитуда
результирующего колебания А=A0/r1 + A0/r2
В точках, где
наблюдается
интерференционный
минимум:
амплитуда
результирующего колебания А=|A0/r1+A0/r2|; m=0, 1, 2, ..., называется
соответственно порядком нтерференционного максимума или
минимума.
34.
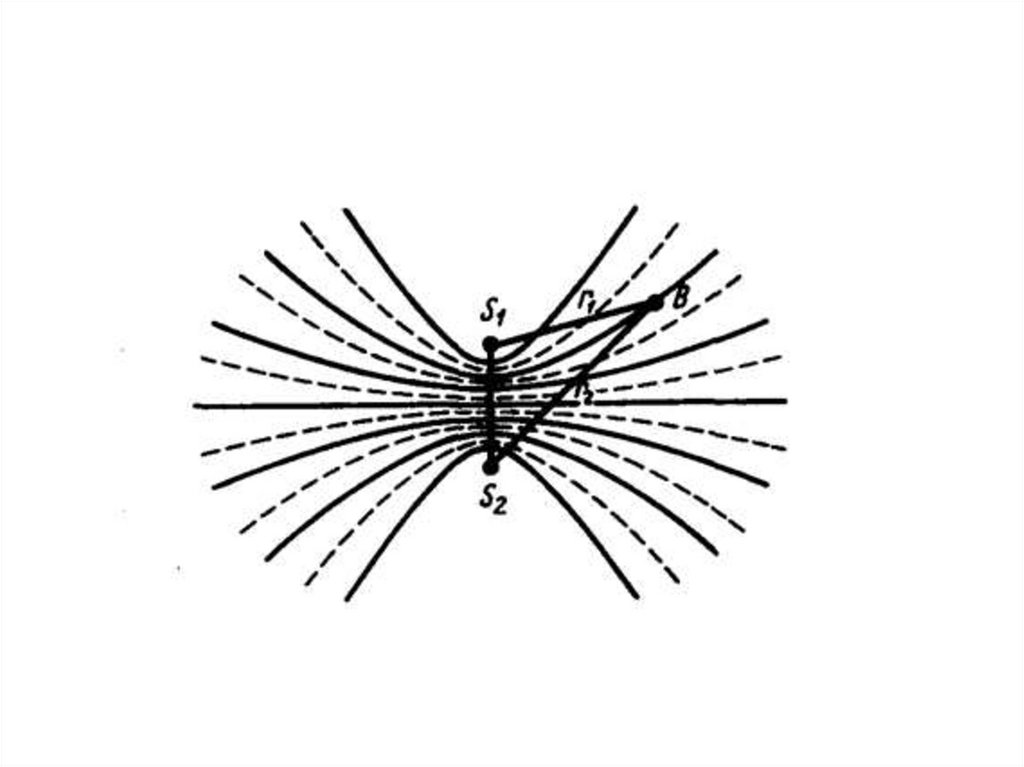
Выражение представляет собой уравнение гиперболы сфокусами в точках S1 и S2. Следовательно,
геометрическое место точек, в которых наблюдается
усиление или ослабление результирующего колебания,
представляет собой семейство гипербол (рис. 221),
отвечающих условию ( 1 – 2)=0. Между двумя
интерференционными максимумами (на рис. 221
сплошные линии) находятся интерференционные
минимумы (на рис. 221 штриховые линии).
35.
36.
Стоячие волныОсобым случаем интерференции являются стоячее волны — это
волны, образующиеся при наложении двух бегущих воли,
распространяющихся навстречу друг другу с одинаковыми
частотами и амплитудами, а в случае поперечных волн и
одинаковой поляризацией.
Для вывода уравнения стоячей волны предположим, что две
плоские волны распространяются навстречу друг другу вдоль оси
х в среде без затухания, причем обе волны характеризуются
одинаковыми амплитудами и частотами. Кроме того, начало
координат выберем в точке, в которой обе волны имеют
одинаковую начальную фазу, а отсчет времени начнем с момента,
когда начальные фазы обеих волн равны нулю. Тогда
соответственно уравнения волны, распространяющейся вдоль
положительного направления оси х, и волны,
распространяющейся ей навстречу, будут иметь вид
37.
Сложив эти уравнения и учитывая, что k=2v/X (см.(154.3)), получим уравнение стоячей волны:
Из уравнения стоячей волны (157.2) вытекает, что в
каждой точке этой волны происходят колебания той же
частоты с амплитудой Aст=|2А cos (2 х/ )|, зависящей
от координаты х рассматриваемой точки.
38.
амплитуда колебаний обращается в нуль. Точки, в которых амплитудаколебаний максимальна (Аст=2А), называются пучностями стоячей
волны, а точки, в которых амплитуда колебаний равна нулю (Aст=0),
называются узлами стоячей волны. Точки среды, находящиеся в
узлах, колебаний не совершают.
Из выражений (157.3) и (157.4) получим соответственно
координаты пучностей и узлов:
39.
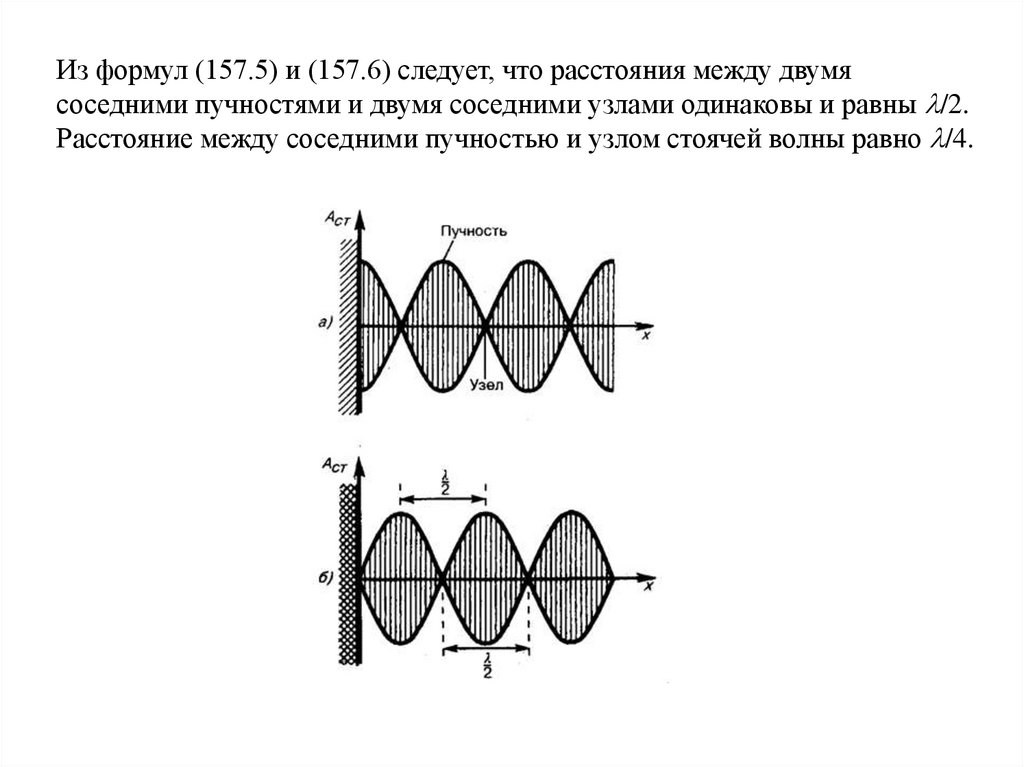
Из формул (157.5) и (157.6) следует, что расстояния между двумясоседними пучностями и двумя соседними узлами одинаковы и равны /2.
Расстояние между соседними пучностью и узлом стоячей волны равно /4.
40.
В отличие от бегущей волны, все точки которой совершаютколебания с одинаковой амплитудой, но с запаздыванием по фазе (в
уравнении (157.1) бегущей волны фаза колебаний зависит от
координаты х рассматриваемой точки), все точки стоячей волны
между двумя узлами колеблются с разными амплитудами, но с
одинаковыми фазами (в уравнении (157.2) стоячей волны аргумент
косинуса не зависит от х). При переходе через узел множитель
2Acos(2 x/ ) меняет свой знак, поэтому фаза колебаний по разные
стороны от узла отличается на , т. е. точки, лежащие по разные
стороны от узла, колеблются в противофазе.
41.
Если рассматривать бегущую волну, то в направлении еераспространения переносится энергия колебательного движения. В
случае же стоячей волны переноса энергии нет, так как падающая и
отраженная волны одинаковой амплитуды несут одинаковую энергию
в противоположных направлениях. Поэтому полная энергия
результирующей стоячей волны, заключенной между узловыми
точками, остается постоянной. Лишь в пределах расстояний, равных
половине длины волны, происходят взаимные превращения
кинетической энергии в потенциальную и обратно
42.
Звуковые волныЗвуковыми (или акустическими) волнами называются
распространяющиеся в среде упругие волны, обладающие частотами в
пределах 16—20 000 Гц. Волны указанных частот, воздействуя на слуховой
аппарат человека, вызывают ощущение звука. Волны с < 16 Гц
(инфразвуковые) и > 20 кГц (ультразвуковые) органами слуха
человека не воспринимаются.
Звуковые волны в газах и жидкостях могут быть только продольными, так
как эти среды обладают упругостью лишь по отношению к деформациям
сжатия (растяжения). В твердых телах звуковые волны могут быть как
продольными, так и поперечными, так как твердые тела обладают
упругостью по отношению к деформациям сжатия (растяжения) и сдвига.
43.
Интенсивностью звука (или силой звука) называетсявеличина, определяемая средней по времени энергией,
переносимой звуковой волной в единицу времени сквозь
единичную площадку, перпендикулярную направлению
распространения волны
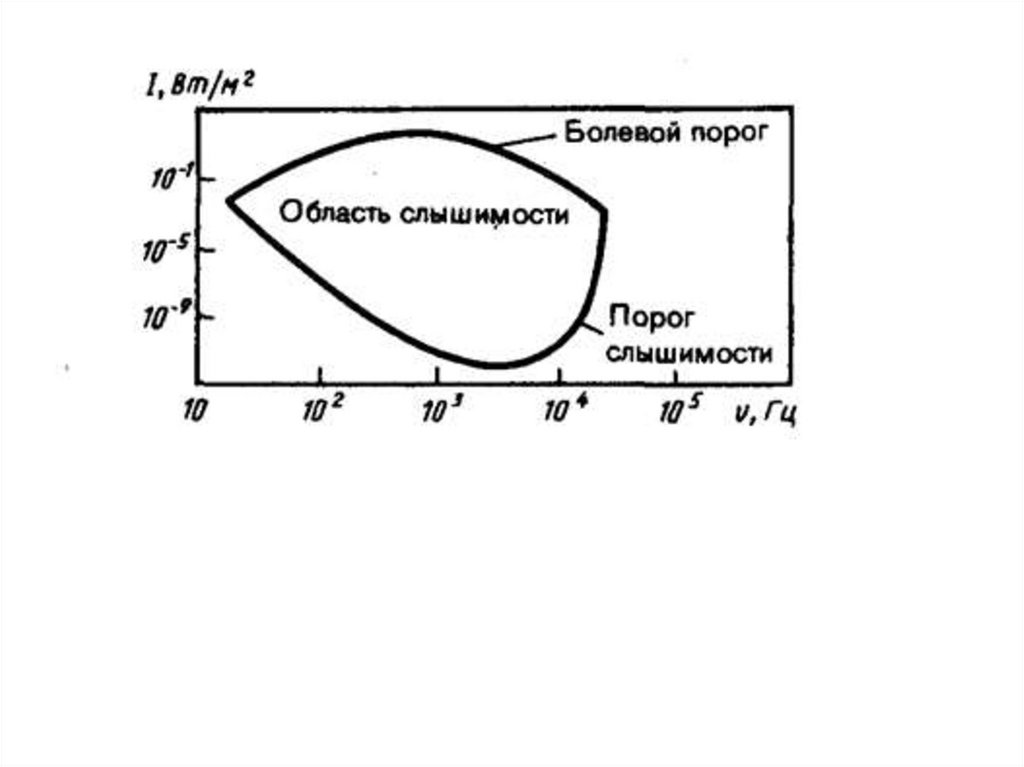
Чувствительность человеческого уха различна для разных частот.
Для того чтобы вызвать звуковое ощущение, волна должна
обладать некоторой минимальной интенсивностью, но если эта
интенсивность превышает определенный предел, то звук не
слышен и вызывает только болевое ощущение. Таким образом,
для каждой частоты колебаний существуют наименьшая (порог
слышимости) и наибольшая (порог болевого ощущения)
интенсивности звука, которые способны вызвать звуковое
восприятие.
44.
45.
Если интенсивность звука является величиной, объективнохарактеризующей волновой процесс, то субъективной
характеристикой звука, связанной с его интенсивностью, является
громкость звука, зависящая от частоты. Согласно физиологическому
закону Вебера — Фехнера, с ростом интенсивности звука громкость
возрастает по логарифмическому закону. На этом основании вводят
объективную оценку громкости звука по измеренному значению его
интенсивности:
где I0 — интенсивность звука на пороге слышимости, принимаемая для
всех звуков равной 10–12 Вт/м2. Величина L называется уровнем
интенсивности звука и выражается в белах (в честь изобретателя
телефона Белла). Обычно пользуются единицами, в 10 раз меньшими,
— децибелами (дБ).
46.
Физиологической характеристикой звука является уровеньгромкости, который выражается в фонах (фон). Громкость для
звука в 1000 Гц (частота стандартного чистого тона) равна 1 фон,
если его уровень интенсивности равен 1 дБ. Например, шум в
вагоне метро при большой скорости соответствует 90 фон, а
шепот на расстоянии 1м — 20 фон.
Реальный звук является наложением гармонических колебаний с
большим набором частот, т. е. звук обладает акустическим
спектром, который может быть сплошным (в некотором
интервале присутствуют колебания всех частот) и линейчатым
(присутствуют колебания отделенных друг от друга
определенных частот).
Звук характеризуется помимо громкости еще высотой и тембром. Высота
звука — качество звука, определяемое человеком субъективно на слух и
зависящее от частоты звука. С ростом частоты высота звука увеличивается,
т. е. звук становится «выше». Характер акустического спектра и
распределения энергии между определенными частотами определяет
своеобразие звукового ощущения, называемое тембром звука. Так,
различные певцы, берущие одну и ту же ноту, имеют различный акустический спектр, т. е. их голоса имеют различный тембр.
47.
48.
ЭНЕРГИЯ УПРУГОЙ ВОЛНЫРассмотрим плоскую продольную волну, распространяющуюся в направлении х:
A cos[
t kx ]
Среда, в которой распространяется волна, обладает
дополнительным запасом энергии. Волна переносит
энергию от источника колебаний в различные точки
среды.
49.
Ww
V
2
2
2
w A sin ( t kx )
Плотность энергии:
Среднее по времени значение:
1
2
2
w A
2
50.
Поток энергии через заданную поверхность(скалярная величина):
W
t
dW
dt
[ ] Вт
Плотность потока энергии (векторная величина):
W
j
S t
[ j ] Вт / м
j dS
j w
2
51.
Определим вектор v , модуль которого равен фазовойскорости волны, а направление совпадает с
направлением переноса энергии (вектор скорости
переноса энергии).
j w v
Для синусоидальных волн эта скорость равна фазовой:
j w
j - вектор Умова.
52.
Среднее по времени значение вектора Умова:j w
1
2
2
j A
2
1
2
2
I j A
2
2
I~A
- интенсивность волны
53.
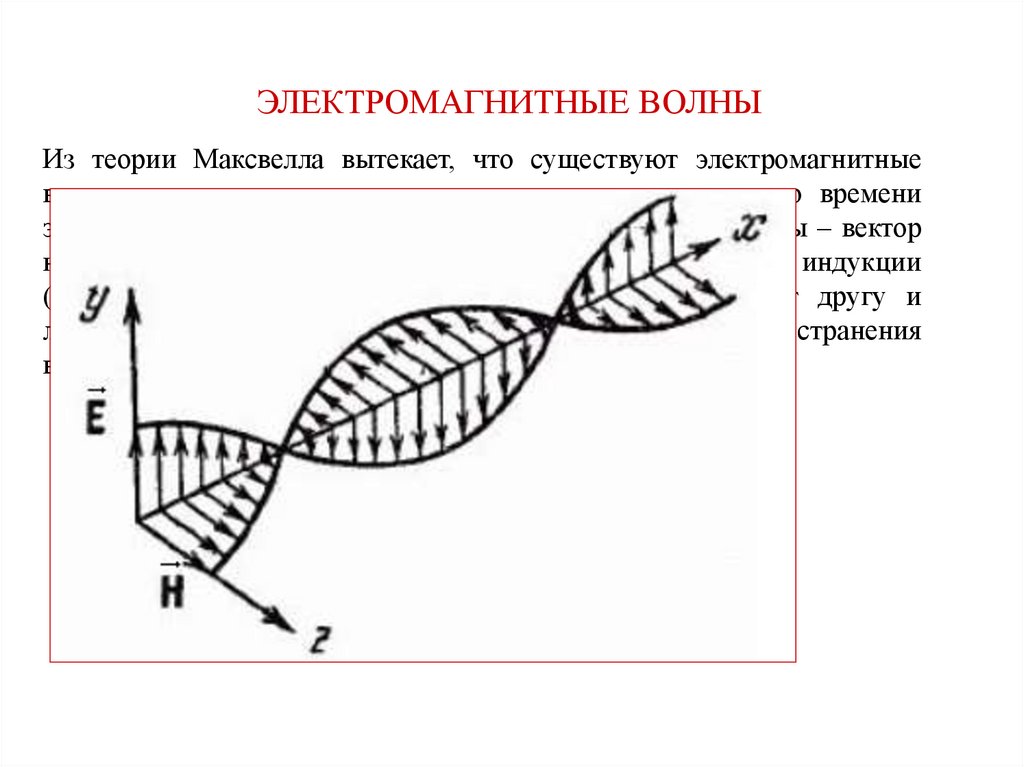
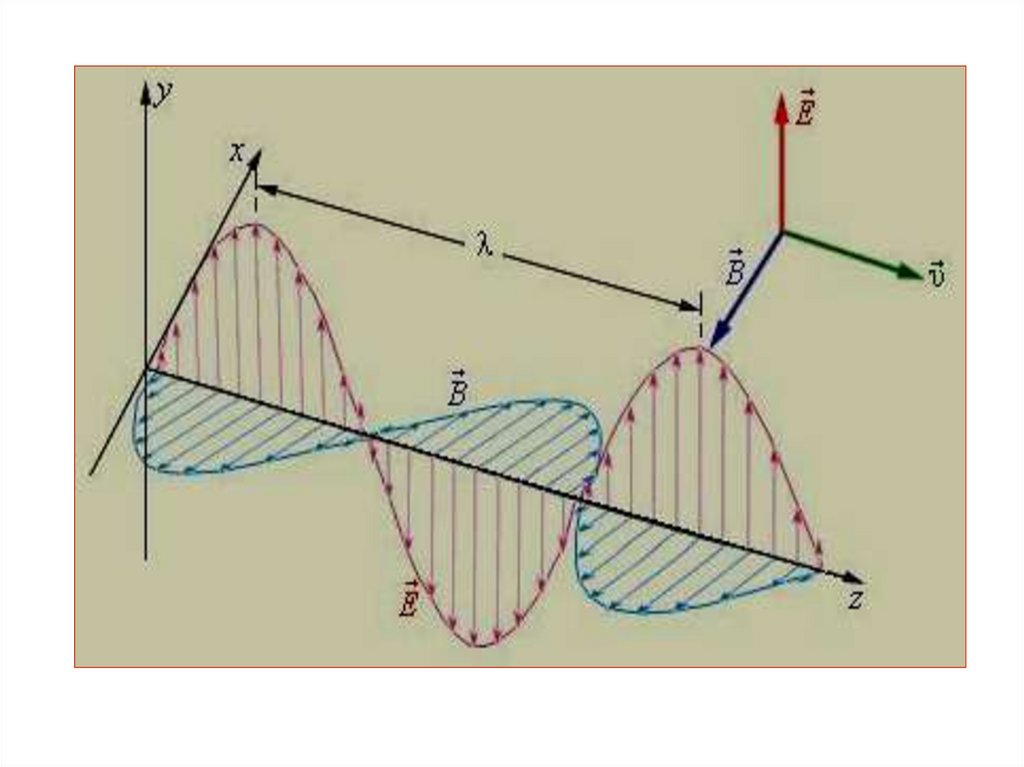
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫИз теории Максвелла вытекает, что существуют электромагнитные
волны, то есть распространяющееся в пространстве и во времени
электромагнитное поле. Электромагнитные волны поперечны – вектор
напряженности электрического поля и вектор магнитной индукции
(напряженности магнитного поля) перпендикулярны друг другу и
лежат в плоскости, перпендикулярной направлению распространения
волны
54.
55.
Волновое уравнение для электромагнитной волны:2
2
2
2
E E E E
x 2 y 2 z 2 c 2 t 2
2
2
2
2
H H H H
x 2 y 2 z 2 c 2 t 2
56.
57.
Электромагнитные волны распространяются в веществе с конечнойскоростью.
c
n
c
n
58.
59.
Закон отражения электромагнитных волн.Угол падения равен углу преломления и лежат в одной плоскости
1 2
Закон преломления электромагнитных волн.
sin n2
n21
sin n1
60.
61.
62.
Уравнения плоской электромагнитной волны, распространяющейся в направлении Х:E y E m cos( t kx )
H z H m cos( t kx )
Умножим Ey на j , а Hz на k.
E E m cos( t kx )
H H m cos( t kx )
63.
В электромагнитной волне происходят взаимные превращенияэлектрического и магнитного полей. Электромагнитные волны
переносят энергию. При распространении волн возникает поток
электромагнитной энергии.
Рассмотрим электромагнитную волну, распространяющуюся в
вакууме:
0 E 2 0 H 2 - плотность энергии (для вакуума)
w wэ wм
2
2
В каждый момент времени wэ = wм (для вакуума и непроводящей среды).
64.
Вектор плотности потока энергии - вектор Пойнтинга:S [ E, H ]
S E H w c - для вакуума
65.
Из теории Максвелла следовало, что электромагнитные волны должныоказывать давление на поглощающее или отражающее тело. Давление
электромагнитного излучения объясняется тем, что под действием
электрического поля волны в веществе возникают слабые токи, то есть
упорядоченное движение заряженных частиц. На эти токи действует сила
Ампера со стороны магнитного поля волны, направленная в толщу
вещества. Эта сила и создает результирующее давление.
Первые эксперименты по определению давления излучения на отражающие
и поглощающие тела были выполнены П. Н. Лебедевым (1900 г.).
66.
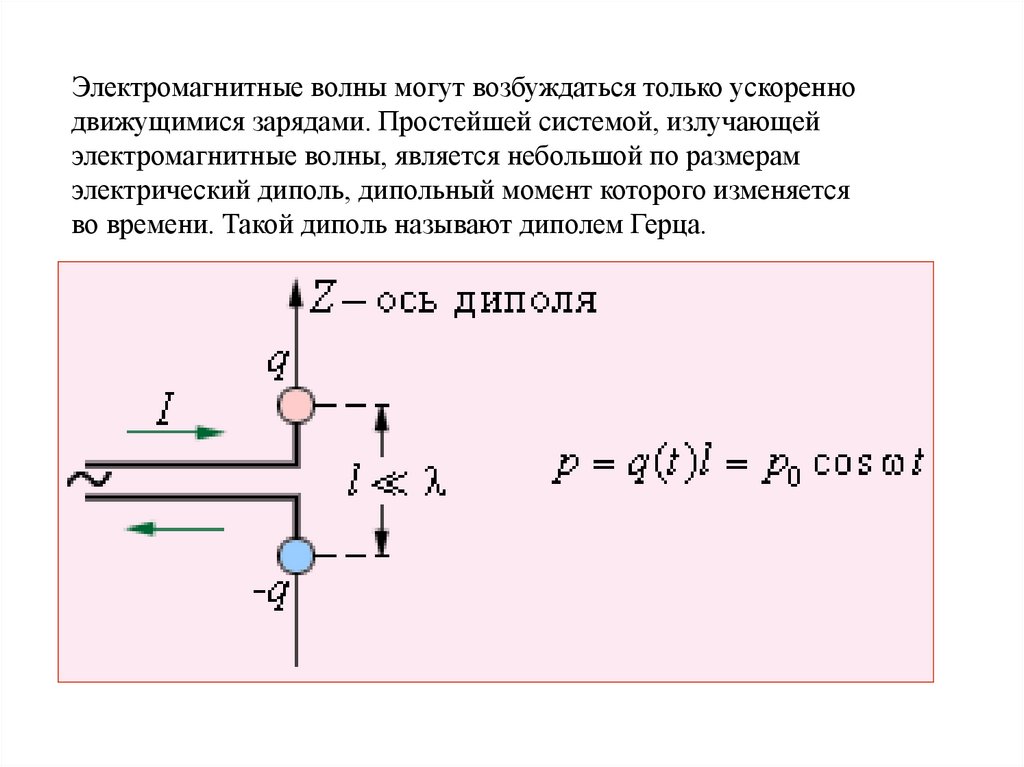
Электромагнитные волны могут возбуждаться только ускореннодвижущимися зарядами. Простейшей системой, излучающей
электромагнитные волны, является небольшой по размерам
электрический диполь, дипольный момент которого изменяется
во времени. Такой диполь называют диполем Герца.










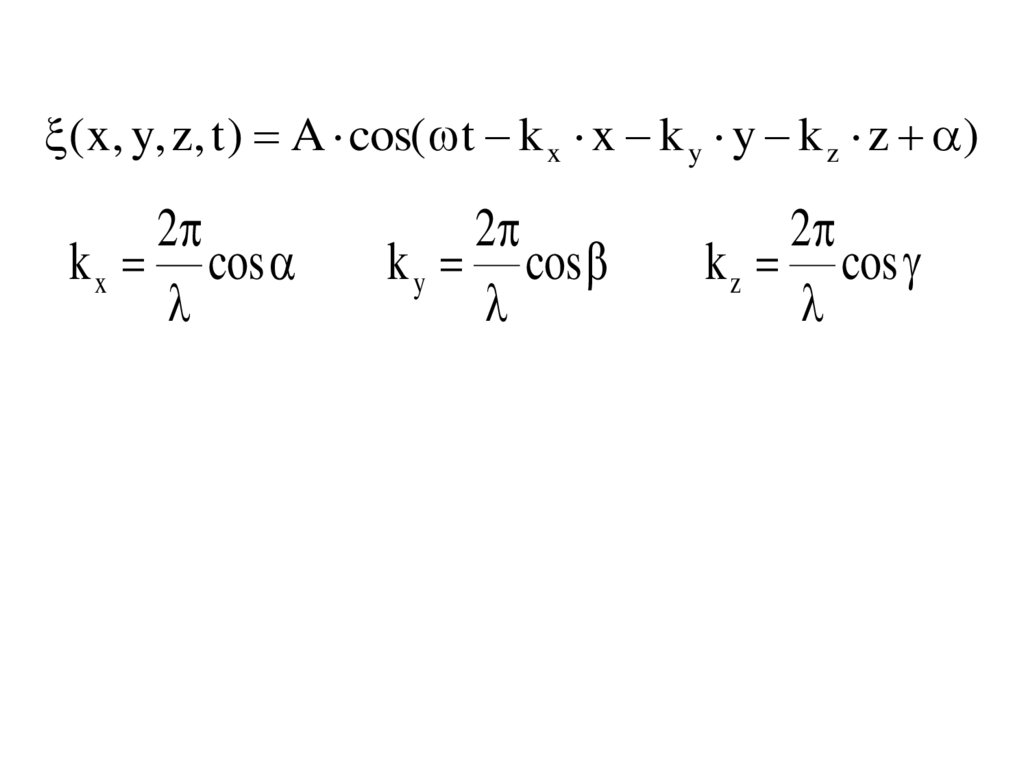































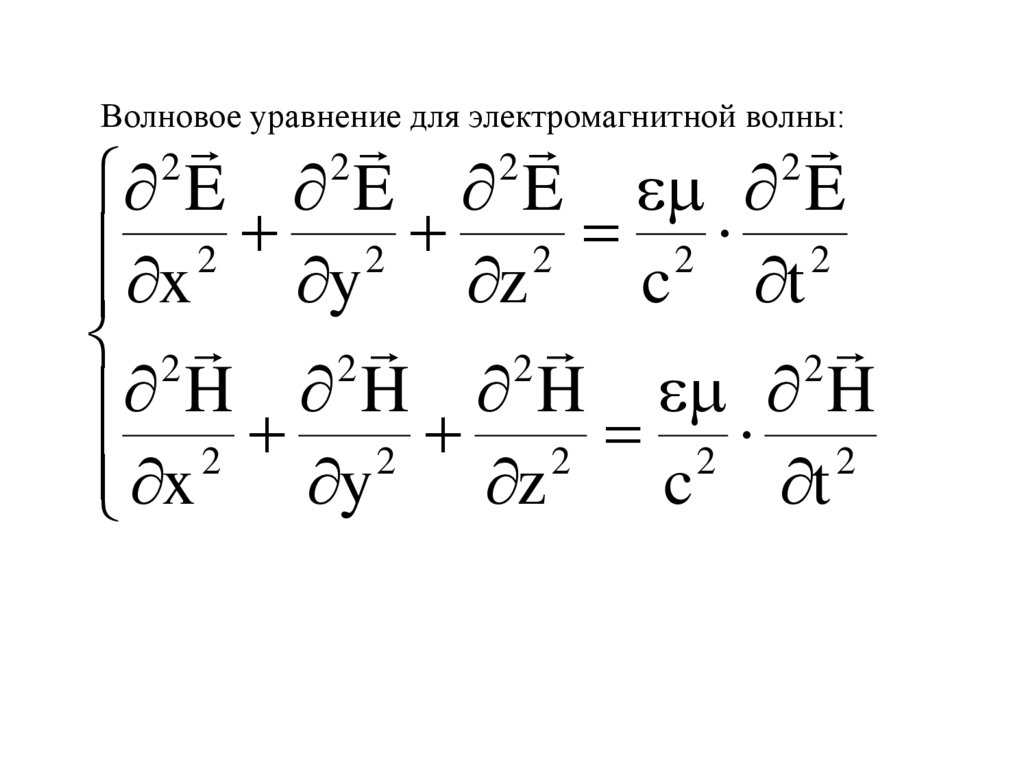










 Физика
Физика








