Волновые процессы

1. Тема 6 ВОЛНОВЫЕ ПРОЦЕССЫ

Волной называется процесс распространения колебаний в пространстве с
течением времени.
Основным свойством всех волн является перенос энергии без переноса
вещества.
Классификация волн: гармонические, затухающие, стоячие.
По своей природе волны бывают механическими (упругими),
например, волны на поверхности жидкости, и электромагнитными.
Механические волны реализуются только в упругой среде в результате
колебаний частиц среды.

2. 6.1 МЕХАНИЧЕСКИЕ ВОЛНЫ

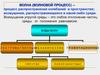
ВОЛНОВЫЕ ВОЗМУЩЕНИЯ
Одиночной волной или волновым
импульсом называется короткое
возмущение, не имеющее
регулярного характера.
Ограниченный ряд
повторяющихся
возмущений
называется цугом волн.
Особое значение в теории волн имеет гармоническая волна, т. е.
неограниченная в пространстве синусоидальная волна, в которой смещение
частиц среды происходит по закону синуса или косинуса.

3. ВОЗНИКНОВЕНИЕ ВОЛНЫ

Если в каком-либо месте упругой среды (твердой, жидкой, газообразной)
возбудить колебания ее частиц, то вследствие взаимодействия между
частицами это колебание будет распространяться в среде от частицы
к частице с некоторой скоростью – в среде возникнет волна.
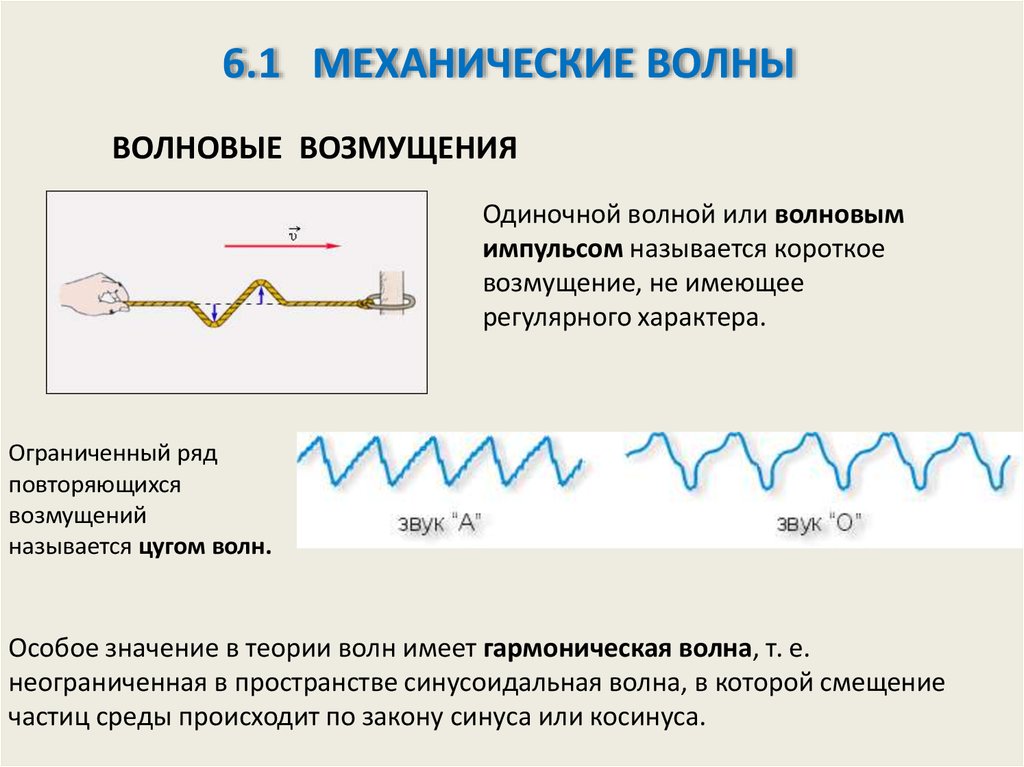
Частицы среды, в которой распространяется волна, не
вовлекаются в поступательное движение, они лишь совершают
колебания около своих положений равновесия.
-2
-1
В продольной волне (1)частицы среды колеблются вдоль направления
распространения волны.
В поперечной волне (2)частицы среды колеблются в направлениях,
перпендикулярных к направлению распространения волны.
В газообразной среде возможно возникновение только продольных
волн. В твердой среде возможно возникновение как продольных, так и
поперечных волн.

4.

Волновой фронт и волновая поверхность
Распространяясь от источника колебаний,
волновой процесс охватывает все новые и
новые области пространства.
Геометрическое место точек, до которых
доходят колебания к данному моменту
времени, называется фронтом волны
или волновым фронтом.
Фронт волны отделяет часть
пространства, уже вовлеченную в волновой
процесс, от области, в которой колебания
еще не возникли.

5.

Геометрическое место точек, колеблющихся в
одинаковой фазе, называется волновой
поверхностью.
Волновую поверхность можно провести через
любую точку пространства, охваченного
волновым процессом. Следовательно волновых
поверхностей существует бесконечно много.
Волновой фронт является одной из волновых поверхностей.

6.

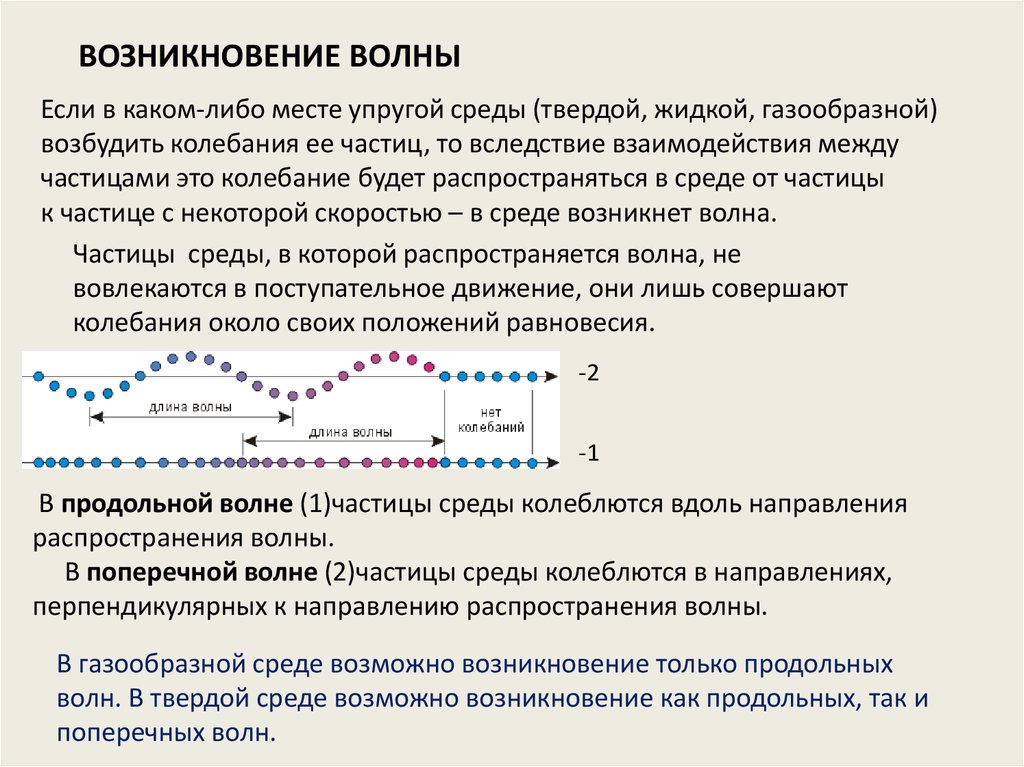
Волновые поверхности могут быть любой
формы.
В простейших случаях они имеют
форму плоскости (плоская волна)
или сферы (сферическая волна).
В плоской волне
волновые поверхности представляют собой
множество параллельных плоскостей, в
сферической волне – концентрических сфер.
Всякий реальный источник волн обладает
конечными размерами. Однако если
ограничиться рассмотрением волны на
расстояниях от источника значительно
превышающих его размеры ( l x ), то источник
можно считать точечным.
В изотропной и однородной среде волна,
порождаемая точечным источником будет
сферической.
На малых расстояниях от источника ( l x )
волну можно считать плоской.

7.

Пусть колебания распространяются с постоянной скоростью вдоль оси OX
в непоглощающей среде. Получим зависимость смещения точки среды ( x, t )
.
Колебания источника, помещенного в начало
координат:
(0, t ) A cos( t 0 )
В т. Р колебания придут на x позже, чем они
возникли в источнике:
p ( x, t ) A cos (t ) 0 A cos t 0 A cos t x 0
Процесс распространения колебаний с фиксированной частотой const
называется монохроматической волной.
( x, t ) A cos t
x 0 (1) – уравнение плоской
монохроматической волны

8.

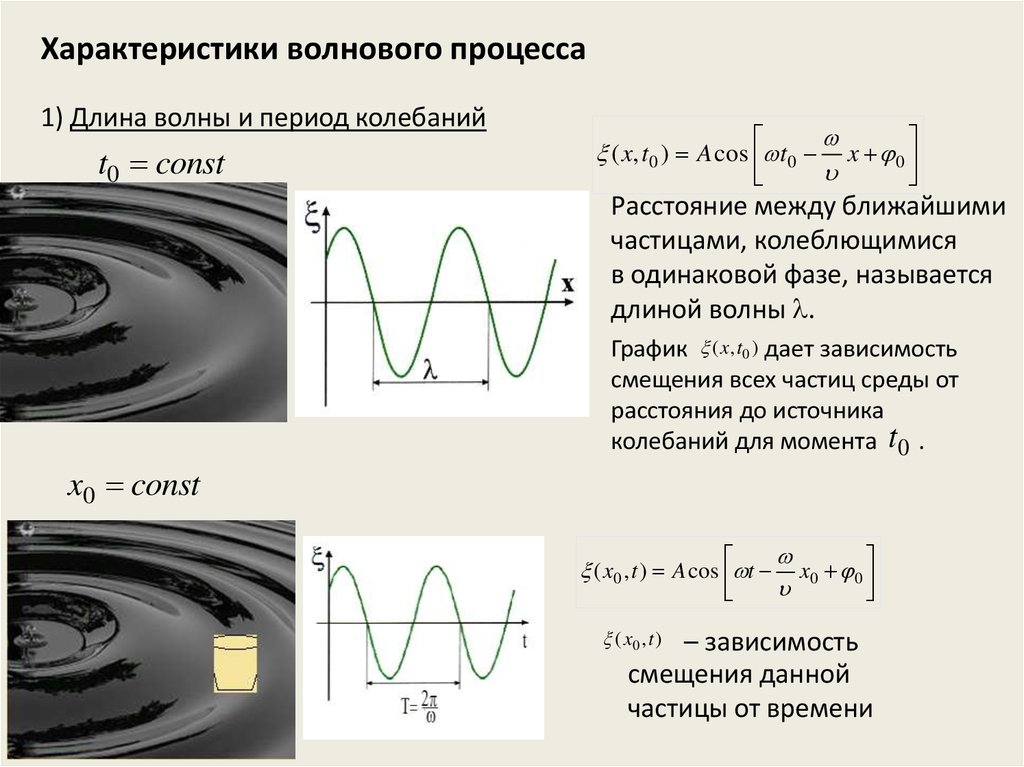
Характеристики волнового процесса
1) Длина волны и период колебаний
t0 const
( x, t 0 ) A cos t 0
x 0
Расстояние между ближайшими
частицами, колеблющимися
в одинаковой фазе, называется
длиной волны .
График ( x, t0 ) дает зависимость
смещения всех частиц среды от
расстояния до источника
колебаний для момента t0 .
x0 const
( x0 , t ) A cos t
( x0 , t )
x0 0
– зависимость
смещения данной
частицы от времени

9.

Найдем связь пространственного λ и временного Т периодов
колебаний. В один и тот же момент времени рассмотрим
колебания в двух точках пространства, фазы колебаний в
которых отличаются на 2p .
1 t0 x1 0
2 t0 x2 0
2 1 ( x2 x1 )
2p
T
2p
T

10.

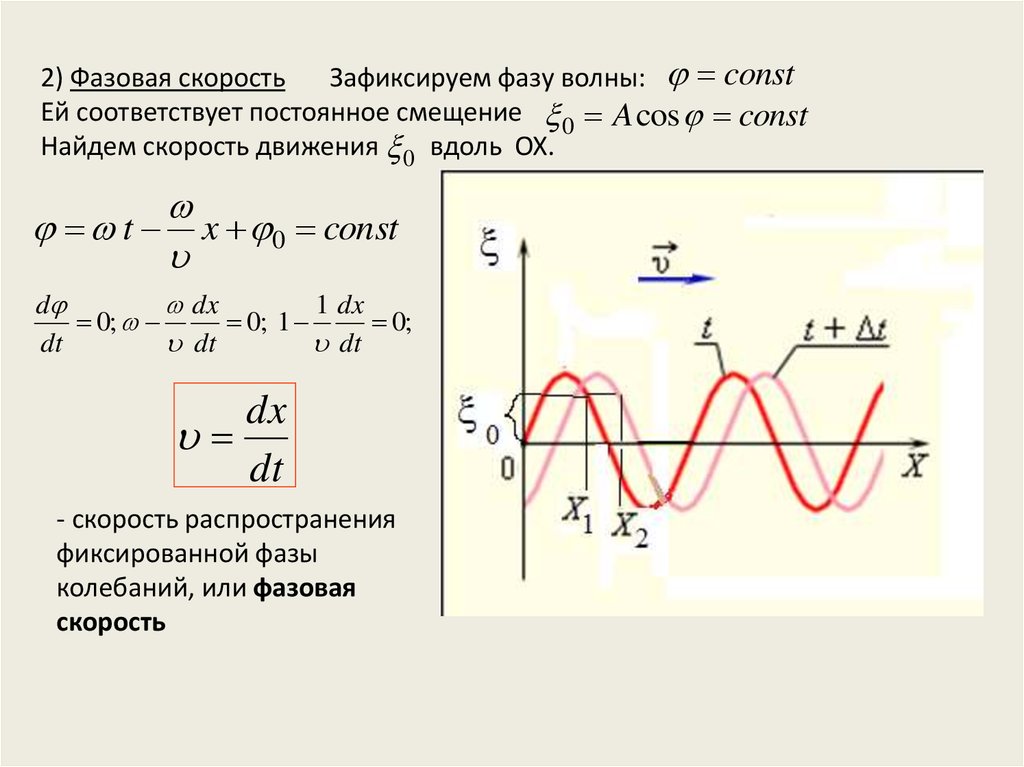
2) Фазовая скорость
Зафиксируем фазу волны: const
Ей соответствует постоянное смещение 0 A cos const
Найдем скорость движения 0 вдоль OX.
t x 0 const
d
dx
1 dx
0;
0; 1
0;
dt
dt
dt
dx
dt
- скорость распространения
фиксированной фазы
колебаний, или фазовая
скорость

11.

3) Волновое число и волновой вектор
2p
По аналогии с T
частота колебаний.
можно записать
2p
k
, где k – пространственная
2p
k
T
2p
k
Волновой вектор
- волновое число (пространственная частота
колебаний).
k n
n 1
- по модулю равен волновому числу и
направлен по нормали к волновой
поверхности в данной точке .

12.

Для плоской волны, распространяющейся в произвольном направлении,
смещение в т. наблюдения Р:
p ( r , t ) A cos( t k r 0 ) (*)
Это уравнение плоской
монохроматической волны ,
распространяющейся в
непоглощающей среде в
общем случае.
Частные случаи:
1) если волна
распространяется вдоль оси
OX:
( x, t ) A cos( t kx 0 )
2) если волна распространяется против оси OX:
( x, t ) A cos( t kx 0 )
(*) – идеальная модель волнового процесса. Монохроматических волн в
природе не существует, любой реальный волновой процесс включает набор
частот в определенном интервале , .
1
2

13.

В изотропной и однородной среде волна, порождаемая точечным
источником будет сферической.
Даже если сферическая волна не поглощается средой, ее амплитуда
уменьшается с удалением от источника по закону 1 r , т.к. энергия
распределяется по поверхности все большего радиуса.
a
Тогда
(r , t ) cos( t kr 0 ).
r
( a – амплитуда на расстоянии от источника, равном единице).
Если в среде распространяется одновременно
несколько волн, то колебания частиц среды
оказываются суммой колебаний, которые
совершали бы частицы при распространении
каждой из волн в отдельности. Следовательно,
волны просто накладываются одна на другую,
не возмущая друг друга. Это утверждение
называется принципом суперпозиции волн.

14.

Стоячие волны.
Стоячие волны – это волны, образующиеся при наложении
двух бегущих волн, распространяющихся навстречу друг другу
с одинаковыми частотами и амплитудами.
Пусть две плоские волны распространяются навстречу друг
другу вдоль оси x в среде без затухания, причем обе волны
характеризуются одинаковыми амплитудами и частотами.
Начало координат выберем в точке, в которой обе волны имеют
одинаковую фазу, а отсчет времени начнем с момента, когда
фазы обеих волн равны нулю.
1 A cos( t kx )
2 A cos( t kx )
14

15.

1 2 A cos( t kx ) cos( t kx )
2 A cos(kx ) cos( t )
2px
2px
Aст ( x ) 2 A cos(
)
2 A cos(
) cos( t )
Точки волны, в которых амплитуда колебаний максимальна,
называются пучностями стоячей волны, а точки, в которых
амплитуда колебаний равна нулю, называются узлами стоячей
волны.
2px
m 0,1,2...
x п m
mp
2px
( m 1 / 2 )p
В случае стоячей волны
переноса энергии нет.
x узл
2
( m 1 / 2 )
2

16.

ВОЛНОВОЕ УРАВНЕНИЕ
Уравнение любой волны , в том числе (*), является решением
дифференциального уравнения, называемого волновым.
Чтобы установить вид волнового уравнения, найдем вторые частные производные по
времени и координатам от уравнения плоской волны:
a cos( t k x x k y y k z z 0 )
2
2
2
k
;
x ;
2
2
x
t
2
2
2
2
k
z .
2
k
;
y
z
y 2
2
2
2
2
Сложим производные по координатам, учтем, что 2 2 2
x
y
z
- оператор Лапласа.
2
2
2
2
2 2 2 2 k 2
x
y
z
k
2 2;
t
2
2
2
2
1
k
1
2
.
2
2
t
2 2
2

17.

- волновое уравнение справедливо для волны
любой природы и с любой формой волнового
фронта, распространяющейся с постоянной
скоростью.
1
2
t
2
2
Для плоской волны, распространяющейся вдоль оси OX, волновое
уравнение имеет вид:
1
2 2
2
x
t
2
2

18.

6.2 электромагнитные
ВОЛНЫ
м
Гц
=103–10–4
Радиоволны:
=3*105–3*1012
Источник излучения – колебательный контур
вибратор Герца ламповый генератор
Световые волны:
инфракрасное излучение 5*10–4–8*10–7
видимый свет
8*10–7–4*10–7
ультрафиолетовое изл. 4*10–7–10–9
6*1011–3.75*1014
3.75*1014–7.5*1014
7.5*1014–3*1017
Источник излучения – лампы, лазеры
Рентгеновское излучение: 2*10–9–6*10–12
1.5*1017–5*1019
Источник излучения – трубки Рентгена
–
Излучение
<6*10–12
>5*1019
Источник излучения – радиоактивный распад
ядерные процессы
космические процессы

19.

6.2.1 Волновое уравнение для электромагнитной волны.
Плоская электромагнитная волна и ее свойства.
Запишем уравнения Максвелла в дифференциальной форме:
B
rot E
t
D
rot H j
t
div D
div B 0
Здесь
E i E x jE y kE z
H i H x jH y kH z
Dx D y Dz
div D
x
y
z
i
rot E
x
Ex
j
y
Ey
k
z
Ez

20.

Пусть среда однородна, изотропна и линейна: тогда
const
const
В этом случае материальные уравнения имеют вид:
D o E
B o H
Пусть в среде нет токов проводимости и свободных зарядов ( 0 , j 0).
Перепишем уравнения Максвелла так, чтобы избавиться от D
div D
H
rot E o
t
div E 0
D
rot H j
t
E
rot H o
t
div B 0
div H 0
B
rot E
t
(1)
(2)
(3)
(4)
и
B
.

21.

Пусть плоская волна распространяется вдоль OX. Тогда E и H зависят
только от x и t .
Анализ записи уравнений Максвелла (1) – (4) в скалярном виде
позволяет сделать следующие выводы:
Вывод 1 Электромагнитные волны поперечны, т.е. векторы E и H
перпендикулярны направлению распространения волны.

22.

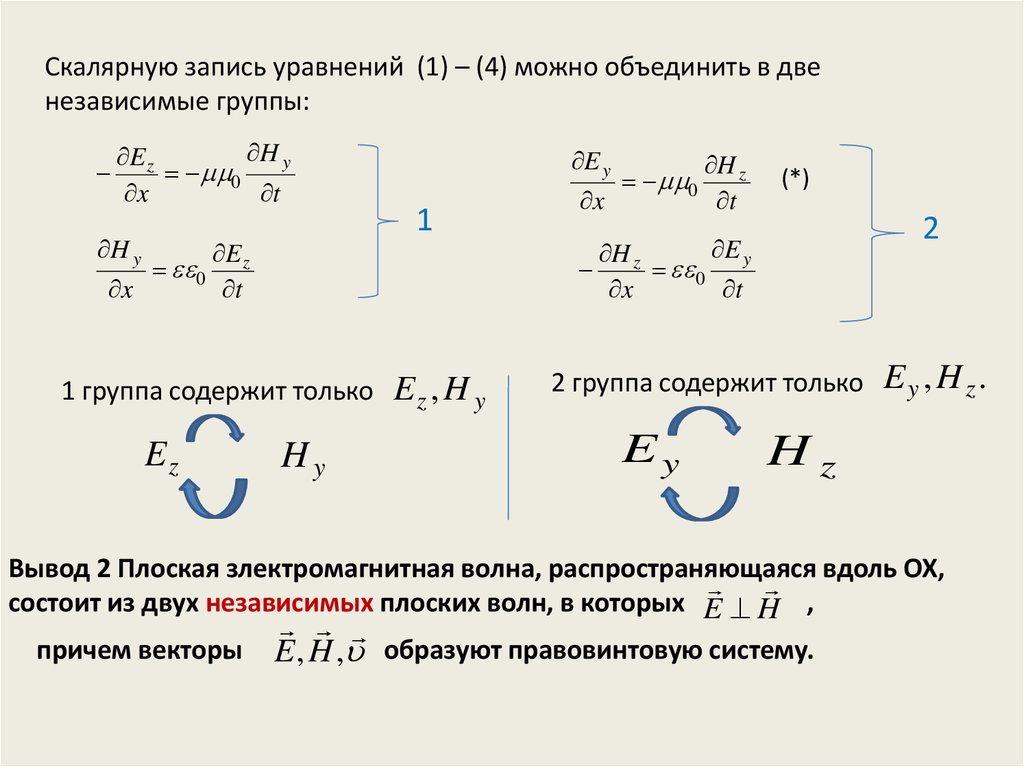
Скалярную запись уравнений (1) – (4) можно объединить в две
независимые группы:
H y
E z
0
x
t
H y
x
0
E z
t
1
x
1 группа содержит только
Ez
E y
Hy
Ez , H y
0
H z
t
(*)
2
E y
H z
0
x
t
2 группа содержит только
Ey
Ey , Hz.
Hz
Вывод 2 Плоская злектромагнитная волна, распространяющаяся вдоль OX,
состоит из двух независимых плоских волн, в которых E H ,
причем векторы E , H , образуют правовинтовую систему.

23.

Систему уравнений 2, описывающую плоскую волну вида
можно преобразовать в систему уравнений (5) – (6):
2E y
x
2
0 0
2E y
t
2
2H z
2H z
0 0
2
x
t 2
(5)
(6)
E
H
Это волновые уравнения для векторов
и
плоской волны, описываемой системой уравнений 2.
0 Ey
0 0
0
,
Hz

24.

Для произвольной электромагнитной волны волновые уравнения имеют вид:
2
2
2
E E E
E
2 2 0 0 2
2
x
y
z
t
2
2
2
2
H H H
H
2 2 0 0 2
2
x
y
z
t
2
При этом фазовая скорость
, то
1
0 0
, а так как скорость света c
c
(7)
Вывод 3 Электромагнитные волны распространяются в однородной
изотропной среде с постоянной фазовой скоростью (7).
В вакууме c , в веществе, т.к. 1, c.
1
0 0

25.

Решения волновых уравнений (5), (6) :
E y E0 cos( t kx 01 )
H z H 0 cos( t kx 02 )
E y
x
0
H z
t
(*)
( k ) E0 sin( t kx 01 ) 0 H 0 sin( t kx 02 )
(16)
Две гармонические функции равны, если равны их амплитуды и фазы:
01 02
Вывод 4 Колебания электрического и магнитного векторов происходят с
одинаковой фазой.
- плоскополяризованная волна
( волна, у которой направление
электрического поля и
направление ее распространения
всегда расположены в одной
плоскости)

26.

Приравняем амплитуды выражения (16):
kE 0 0 H 0
k 0 0
Т.к. векторы E
0 E0 0 H 0
(17)
H
,
колеблются в одинаковых фазах, (17)
справедливо для мгновенных значений модулей этих векторов.
Вывод 5 Мгновенные значения Е и Н в любой точке связаны соотношением :
0 E 0 H
Произвольная плоская электромагнитная монохроматическая волна,
распространяющаяся вдоль OX, - суперпозиция двух волн
0 Ey
0 0
0
H z
0 0
0 H y
Ez
0

27.

В этой волне
E y E01 cos( t kx 01 )
Ez E02 cos( t kx 02 )
При этом результирующий вектор E для некоторого x0
- результат
сложения двух взаимно перпендикулярных колебаний E z и E y в
плоскости YOZ
Обозначим 0 02 01
Траектория движения конца вектора E
со временем в фиксированной плоскости
YOZ представляет собой эллипс:
E 2y
2
E01
E y Ez
E z2
2 2
cos 0 sin 2 0
E01 E02
E02
Так же ведет
себя
вектор H .
Такая волна называется
эллиптически
поляризованной.

28.

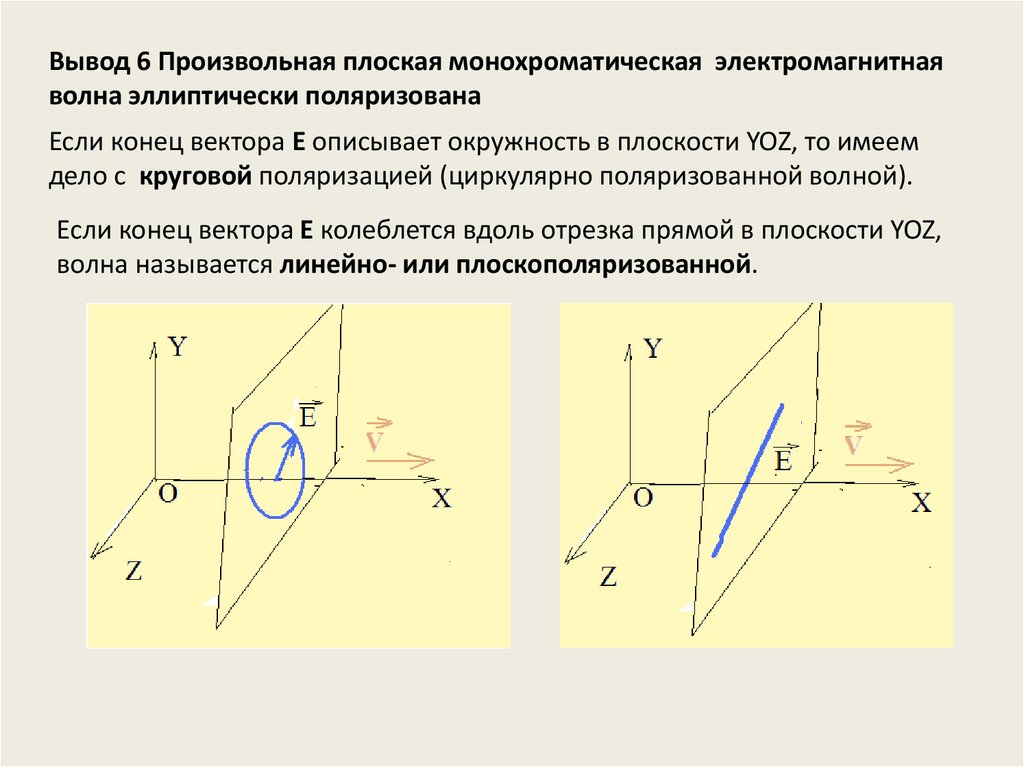
Вывод 6 Произвольная плоская монохроматическая электромагнитная
волна эллиптически поляризована
Если конец вектора Е описывает окружность в плоскости YOZ, то имеем
дело с круговой поляризацией (циркулярно поляризованной волной).
Если конец вектора Е колеблется вдоль отрезка прямой в плоскости YOZ,
волна называется линейно- или плоскополяризованной.

29.

Резюме
Следствием теории Максвелла является поперечность
электромагнитных волн:
векторы Е и Н напряженностей
электрического и магнитного полей волны взаимно перпен–
дикулярны и лежат в плоскости, перпендикулярной вектору v скорости распространения волны, причем векторы Е, Н и v
образуют правовинтовую систему.
Векторы Е и Н всегда колеблются в одинаковых фазах, причем
мгновенные значения Е и Н в любой точке связаны соотношением
0 E 0 H

30.

6.2.2 Энергия электромагнитных волн. Поток энергии и
плотность потока энергии.
В однородной изотропной среде ( , const ) объемная плотность энергии
ЭМ поля
(**)
Для характеристики стационарных полей достаточно понятий энергии и
плотности энергии. Но волны переносят энергию. Перенос энергии волной
характеризуется потоком энергии и плотностью потока энергии.
Поток энергии через данную поверхность – это количество энергии,
переносимое через эту поверхность в единицу времени:
I w dW
dt
(аналогом потока энергии является
электрический ток: I dq ).
dt

31.

По аналогии с электрическим током ( I j dS ) перейдем к
S
дифференциальной характеристике переноса
энергии в окрестности
данной точки – плотности потока энергии jw :
I w jwdS
S
dI w jwdS jwdS cos
dS cos dS
dI w jw dS jw dI w
dS
Плотность потока энергии численно равна энергии поля, перемещаемой
за единицу времени через единичную площадку, перпендикулярную
направлению распространения волны в данной точке.

32.

Выразим jw через объемную плотность энергии ЭМ поля:
dW wV w dS dt
dW jw dS dt
jw w
В векторной форме:
jw w
Плотность потока энергии равна произведению объемной плотности
энергии на фазовую скорость волны; это вектор, совпадающий по
направлению с фазовой скоростью.

33.

6.2.3 Закон сохранения энергии в электромагнитной волне.
Вектор Умова - Пойнтинга
В 6.2.2 получили (**): w
EH
w EH jw
Т.к. векторы Е и Н взаимно перпендикулярны и
образуют с направлением распространения волны
правовинтовую систему, то
EH
EH EH
jw EH
- вектор Умова–Пойнтинга
Вектора Умова–Пойнтинга - это вектор плотности потока энергии,
переносимой электромагнитной волной.

34.

Поток энергии, втекающей в единицу
времени в объем V:
dW
I w EH dS
dt
S
В объеме V эта энергия расходуется на:
1) выделение джоулева тепла;
обозначим мощность джоулевых потерь
P
dQ
dt
2) увеличение энергии ЭМ поля WV внутри этого объема
dWV
Iw P
dt
dWV
w
dV
dt
t
V
- закон сохранения энергии в электромагнитной волне
Поток энергии ЭМ поля, втекающий в объем V, расходуется на выделение
джоулева тепла и увеличение энергии ЭМ поля внутри этого объема.

35.

6.2.4 СВЕТОВАЯ ВОЛНА
Оптическим излучением или светом называются электромагнитные
волны, длины которых в вакууме лежат в диапазоне от 10 нм до
0.5 мм.
К оптическому излучению относятся инфракрасное, видимое и
ультрафиолетовое излучение.
Интенсивность ЭМ волны – среднее по t значение плотности потока
энергии, переносимого волной.
jw EH E0 H 0 sin 2 ( t kx 0 )
sin ( t kx 0 )
2
t T
1
2
1
1 0 2
jw E0 H 0
E0
2
2 0
I св E02
Под интенсивностью света понимают просто квадрат амплитуды вектора
напряженности электрического поля

36.

Экспериментально установлено, что действие света на фотоэлемент,
фотопленку, флуоресцирующий экран и другие устройства для его
регистрации определяется вектором электрической напряженности Е
электромагнитного поля световой волны. Поэтому иногда этот вектор
называют световым вектором. К такому же выводу приводит и классическая
электронная теория, согласно которой процессы, вызываемые
светом в веществе, связаны с действием электрического поля световой волны
на заряженные частицы вещества – электроны и ионы.
Геометрическая оптика основная модель – идеальный световой луч
Под световыми лучами понимаются нормальные к волновым
поверхностям линии, вдоль которых распространяется поток
световой энергии.
Основные законы геометрической оптики
1) В однородной среде свет распространяется прямолинейно (
этот закон нарушается явлением дифракции)
2) Лучи света при пересечении не возмущают друг друга
( нарушается явлением интерференции)
3) Закон отражения
1 2

37.

4) Закон преломления на границе двух сред
sin n2
n21
sin n1
абсолютным показателем преломления среды называется величина n, равная
отношению скорости с электромагнитных волн в вакууме к их фазовой скорости v в
среде:
n
c
Относительным показателем преломления двух сред (второй среды по отношению
к первой) называется величина n21, равная отношению показателей преломления
этих сред:
n2 c 1 1
n21
n1 2 c 2
Для оптически прозрачных (неферромагнитных ) сред
2 2
2
n21
1 1
1

38.

Из опыта : частота колебаний векторов Е, Н не зависит от среды
распространения волны:
const
cT 0
n
T
c
0
n
- длина волны уменьшается в оптически более плотных
средах.