Устойчивость_1_л

1. Волгоградский государственный технический университет

Кафедра «Строительная механика»
ДИНАМИКА И УСТОЙЧИВОСТЬ СООРУЖЕНИЙ
ЧАСТЬ ВТОРАЯ
УСТОЙЧИВОСТЬ СООРУЖЕНИЙ
к.т.н., доцент Рекунов Сергей Сергеевич

2.

3.

4.

5. Система устойчива, если после снятия нагрузки, выведшей систему из прямолинейного равновесия, возвращается в исходное

прямолинейное состояние.
Переход системы из устойчивого состояния в
неустойчивое называется потерей устойчивости.
Граница этого перехода называется критическим
состоянием системы, а соответствующие нагрузки –
критическими.

6. Равновесие называется устойчивым, если при любом малом отклонении от положения равновесия тело возвращается в исходное

положение после устранения причины, вызвавшей
это отклонение.

7.

Равновесие называется неустойчивым, если при
любом малом отклонении от положения равновесия тело
не возвращается в исходное состояние, а всё далее
отклоняется от него.

8.

Равновесие называется безразличным, если тело,
отклонённое
от
положения
равновесия,
равновесии и в новом положении.
остаётся
в

9.

Устойчивость формы равновесия упругой системы
зависит от её геометрических параметров (размеры
поперечного сечения, длина, высота и др.), материала,
величины и направления сжимающих сил.

10.

Формы потери устойчивости:
Первая форма (по Эйлеру):
система после потери устойчивости остаётся в
равновесии;
Вторая форма:
величина
продольной
силы
достигает
такого
значения, что деформации начинают расти без
дальнейшего увеличения нагрузки.

11.

Критической силой называют такую силу, при очень
незначительном превышении которой, возможно появление
новой, искривлённой формы равновесия.

12.

Основные способы расчёта конструкции на устойчивость:
1. Статический
При расчёте систем статическим способом используются
дифференциальные уравнения бесконечно малого элемента.
2. Энергетический
Энергетический способ основан на исследовании величины
приращения потенциальной энергии деформации при
отклонении системы от исходного равновесного состояния.
3. Динамический
Составляется уравнение собственных колебаний сжатого
осевой силой стержня и определяется значение критической
силы, при которой частота собственных колебаний будет равна
нулю.

13. Вывод формулы Эйлера для шарнирно закреплённого стержня

14.

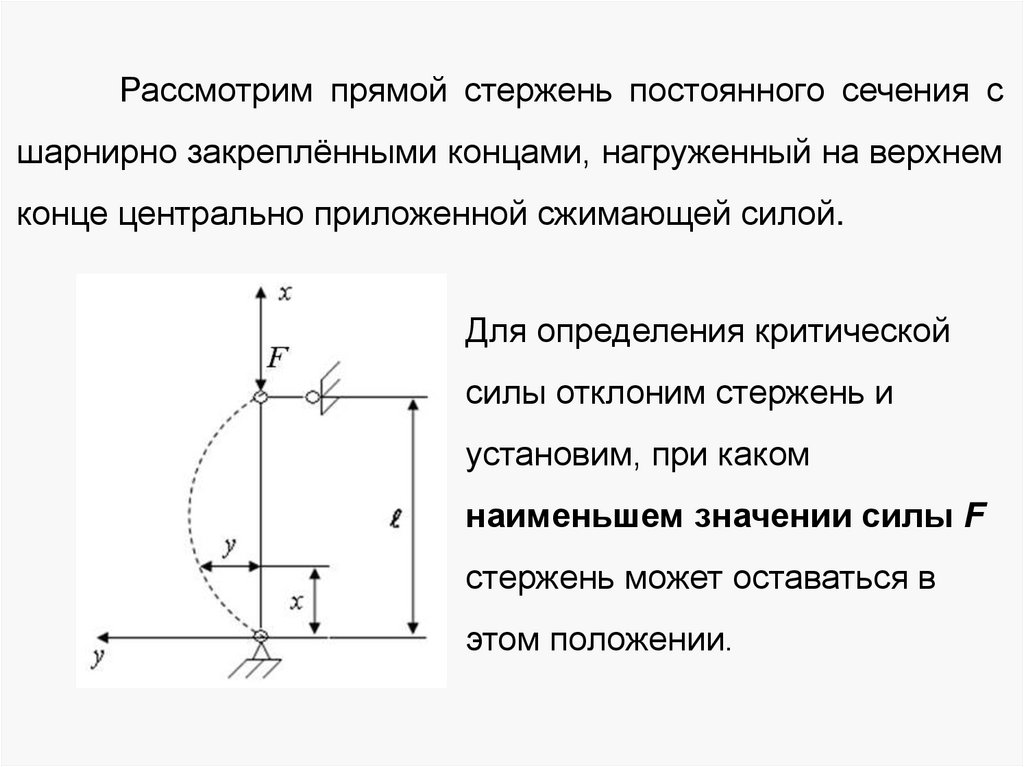
Рассмотрим прямой стержень постоянного сечения с
шарнирно закреплёнными концами, нагруженный на верхнем
конце центрально приложенной сжимающей силой.
Для определения критической
силы отклоним стержень и
установим, при каком
наименьшем значении силы F
стержень может оставаться в
этом положении.

15.

Выражение для кривизны изогнутой оси стержня при
малых прогибах по сравнению с длиной стержня:
2
M
d y
2
EI
dx
Изгибающий момент в сечении, расположенном на
расстоянии x от нижней опоры:
M = - F Чy

16.

После подстановки имеем:
d y
F Чy
=2
dx
EI
2
2
или
d y
2
k
y 0
2
dx
Решение последнего дифференциального уравнения
имеет следующий вид:
y A cos kx B sin kx

17.

Постоянные интегрирования A и B можно определить
из граничных условий:
1. При x = 0 прогиб y = 0 :
0 A cos 0 B sin 0
A 1 0 A 0
Напоминание:
y A cos kx B sin kx

18.

2. При x = l прогиб y = 0 :
B sin kl 0
Таким образом, необходимо принять sin kl 0 или с учётом
F
выражения k =
:
EI
2
F
sin l
=0
EI
®
F
l
= pn
EI
где n – может быть равно 0, 1, 2, ...
В нашем случае n ≠ 0, так как в противном случае F = 0, что
не соответствует условию задачи.
Напоминание:
y A cos kx B sin kx

19. Наименьшее значение F = Fкр можно получить при n =1, тогда:

l
Fкр
EI
2
= p
или
p EI
Fкр = 2
l
Данное выражение – формула Эйлера для заданного
шарнирного вида закрепления.

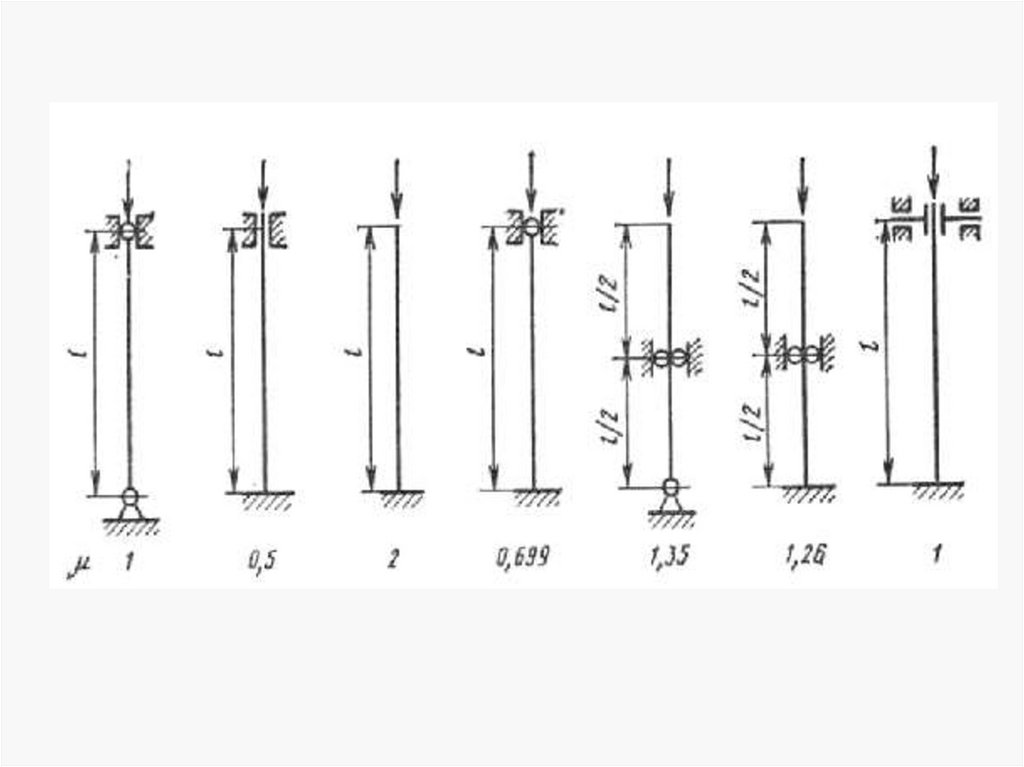
20.

Для других случаев закрепления формула Эйлера
имеет следующий вид:
EI EI
Fкр
2
2
l
l
2
2
где – коэффициент привидения длины,
учитывающий условия закрепления концов стойки;
- коэффициент устойчивости.

21.

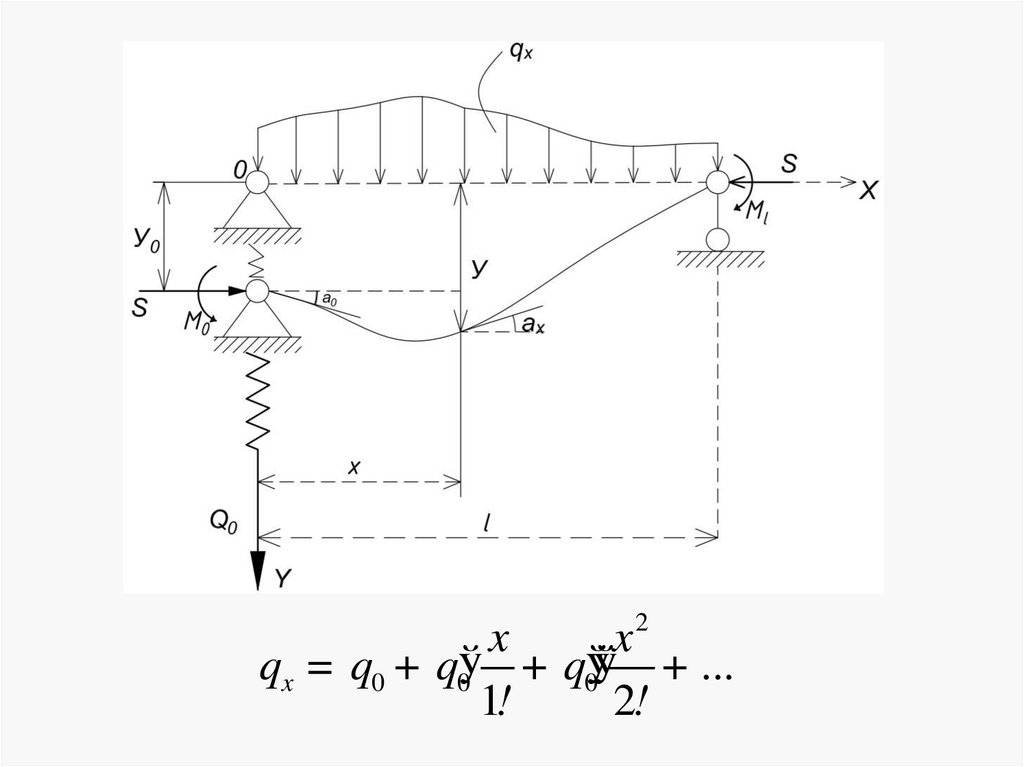
22. Общее уравнение упругой линии сжато-изогнутого стержня

23.

2
x
x
qx = q0 + q0ў + q0ўў + ...
1!
2!

24.

Уравнение ординаты упругой линии:
sin kx
1- sin kx
y x = y0 + y0ў
+ M0
+
2
k
k
k 2 x2
cos kx - 1 +
kx - sin kx
2 .
+ Q0 q
+
q
0
3
k
k4

25.

Уравнение для тангенса угла наклона упругой линии:
sin kx
y xў = a x = y0ўcos kx + M 0
+
k
1- cos kx
kx - sin kx
+ Q0 q
+ q0
.
2
3
k
k

26.

Уравнение для изгибающего момента в сечении балки:
М x = EIy ўў= - y0ўk EI sin kx + M 0 cos kx +
sin kx
1- cos kx
+ Q0 q
+ q0
.
2
k
k

27.

Уравнение для поперечной силы в сечении балки:
2
ў
Qx = - y0 k EI cos kx - M 0k sin kx +
sin kx
+ Q0 q cos kx + q0
.
k

28.

y0ў= a 0 - начальный угол поворота
M 0 , Q0q - момент и перерезывающая сила от
поперечной нагрузки и нормальных сил к
оси стержня реакций
Q0 q
M0
при x = 0
M0 =
, Q0 q =
EI
EI

29. Упругие реакции для сжато-изогнутого стержня в единичных состояниях

30.

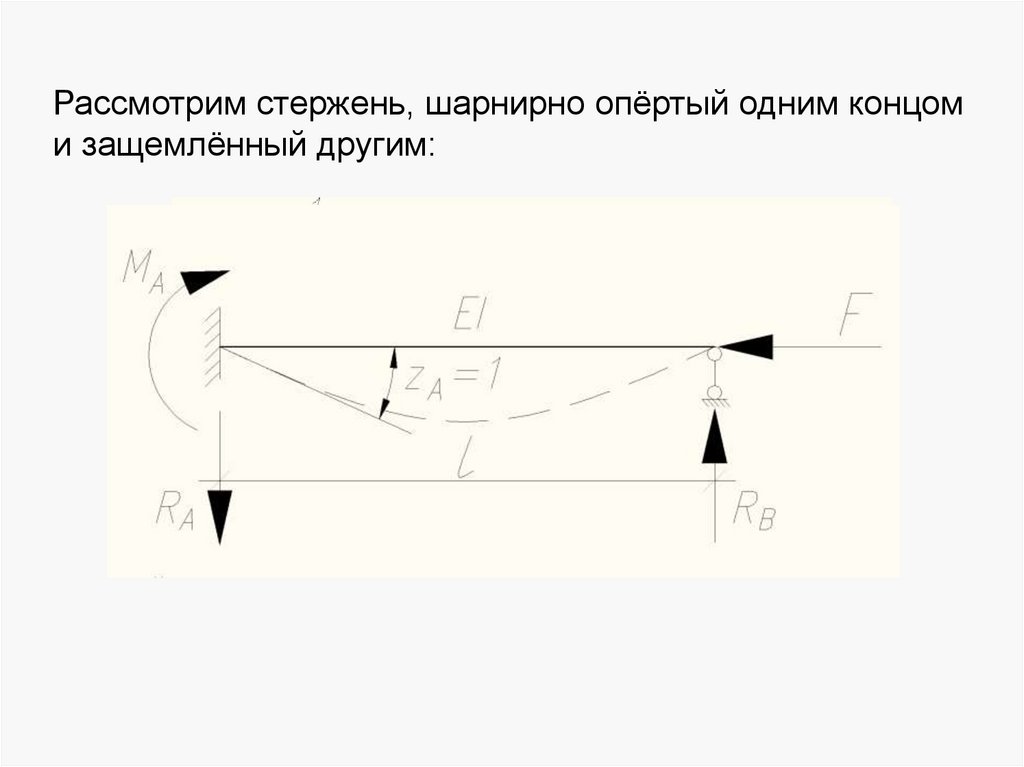
Рассмотрим стержень, шарнирно опёртый одним концом
и защемлённый другим:

31.

yB 0
sin n M A 1- cos n M A n - sin n
yB = z A
Ч
+
Ч
=0
2
3
k
EI
k
EI l
k
Отсюда, при z A = 1 :
3EI
n2
3EI
MA =
Ч
=
j 1 (n )
l 3(1- n / tgn )
l
M A 3EI
RA = RB =
= 2 j 1 (n )
l
l

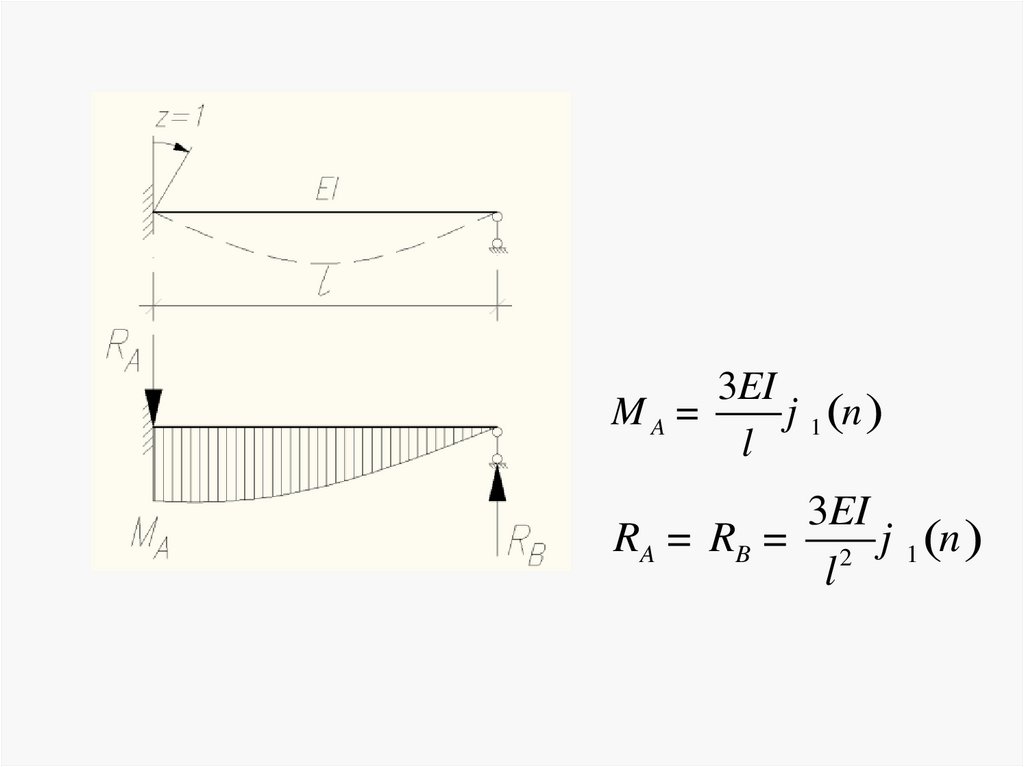
32.

3EI
MA =
j 1 (n )
l
3EI
RA = RB = 2 j 1 (n )
l

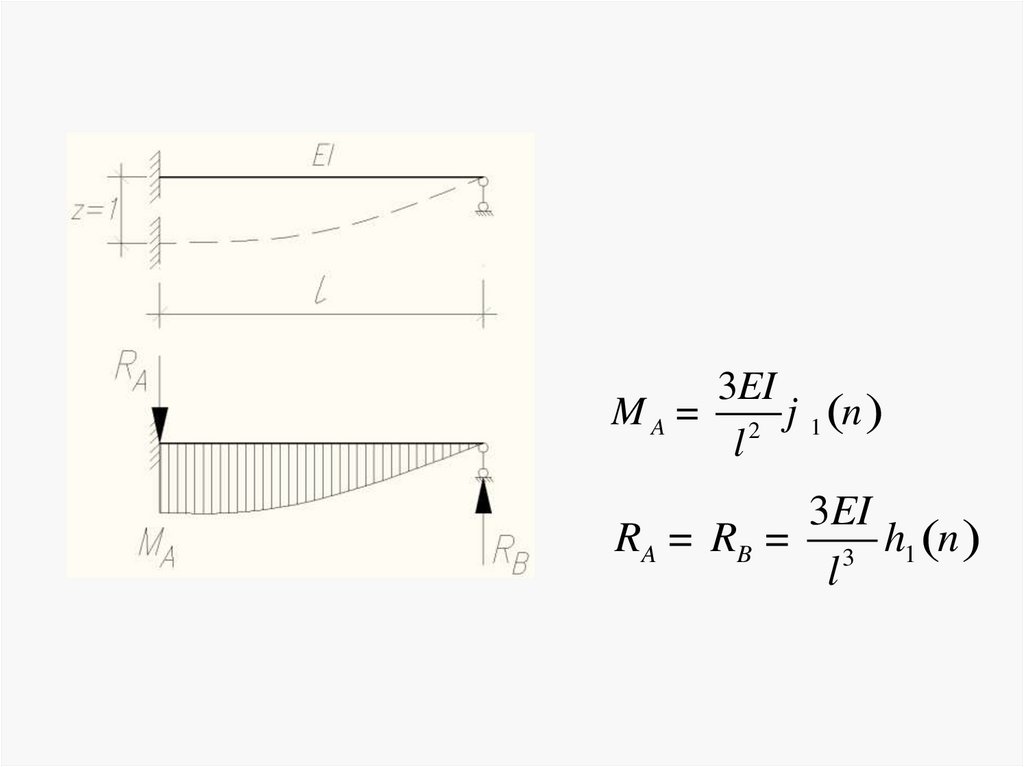
33.

3EI
M A = 2 j 1 (n )
l
3EI
RA = RB = 3 h1 (n )
l

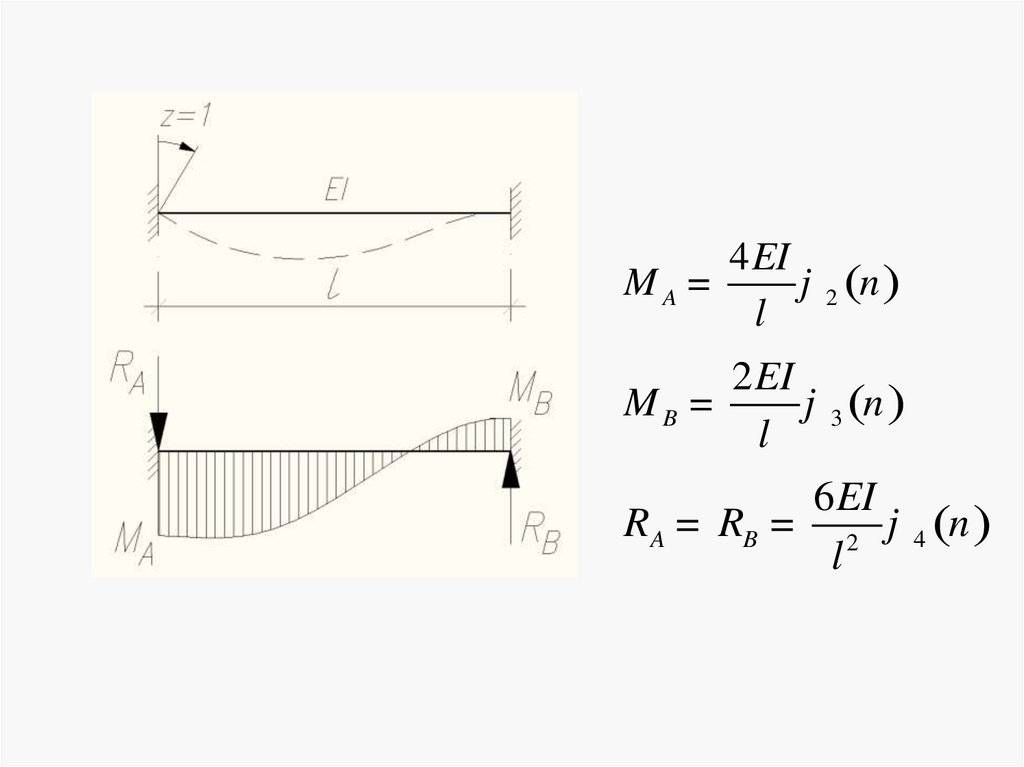
34.

4 EI
MA =
j 2 (n )
l
2 EI
MB =
j 3 (n )
l
6 EI
RA = RB = 2 j 4 (n )
l

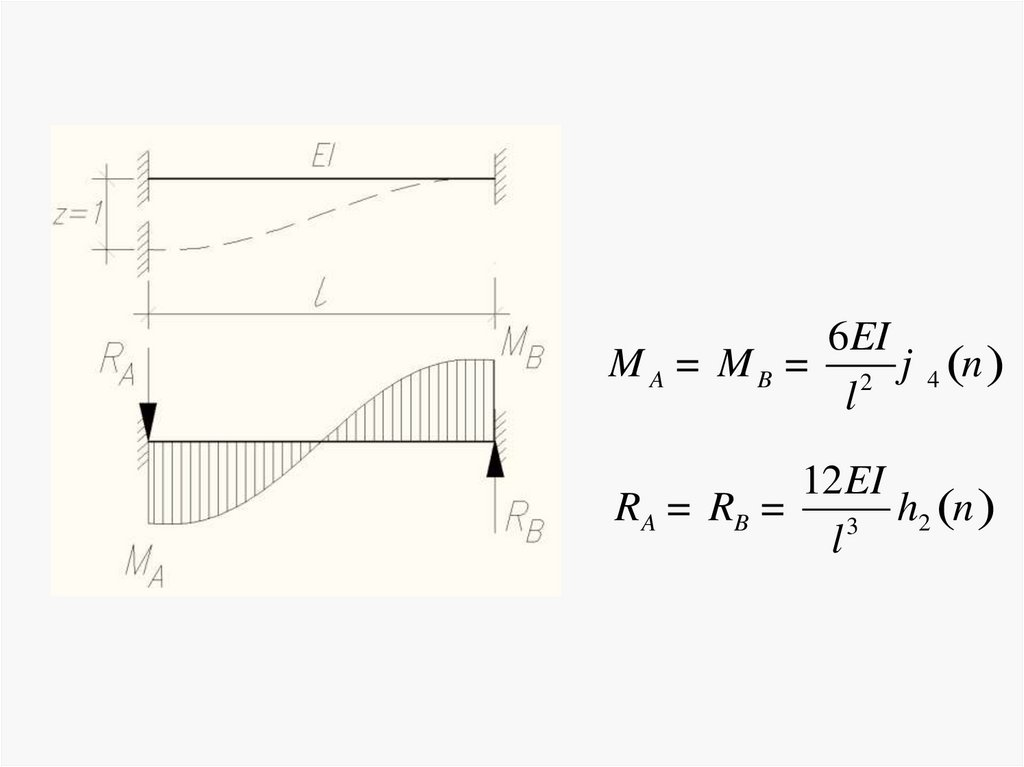
35.

6 EI
M A = M B = 2 j 4 (n )
l
12 EI
RA = RB = 3 h2 (n )
l

36. РАСЧЁТ КОНСТРУКЦИЙ НА УСТОЙЧИВОСТЬ

37.

Допущения к расчёту рам на устойчивость
1. Нагрузка прикладывается в узлы рамы;
2. Стержни несжимаемы и нерастяжимы;
3. Деформации стержней не учитываются;
4. Приращения продольной силы и изменение угла
наклона касательной при потере устойчивости
не учитываются;
5. Криволинейная форма равновесна.

38. Расчёт рам на устойчивость методом перемещений

39.

Алгоритм расчёта
1.Определяется количество неизвестных по методу
перемещений ;
2. Основная система метода перемещений;
3. Определитель устойчивости
r11 r12
r21 r22
D
... ...
rn1 rn 2
... r1n
... r2 n
0
... ...
... rnn
4. Построение единичных эпюр M1 , M 2 , ...,M n ;
5. Подсчёт коэффициентов определителя устойчивости;

40.

6. Подсчёт параметра гибкости для каждого стержня по
формуле
F
v= l
EI
7. Решение определителя;
8. Определение по графику величины параметра vкр ;
9. Определение величины критической силы
Fкр =
2
vкр
EI
l
2
.

41. Спасибо за внимание!