9 класс_урок 10. Презентация

1. Граф. Весовая матрица графа. Длина пути между вершинами графа. Вычисление количества путей в направленном ациклическом графе

ГРАФ.
ВЕСОВАЯ МАТРИЦА ГРАФА.
ДЛИНА ПУТИ МЕЖДУ ВЕРШИНАМИ ГРАФА.
ВЫЧИСЛЕНИЕ КОЛИЧЕСТВА ПУТЕЙ В
НАПРАВЛЕННОМ АЦИКЛИЧЕСКОМ ГРАФЕ

2. Что такое граф?

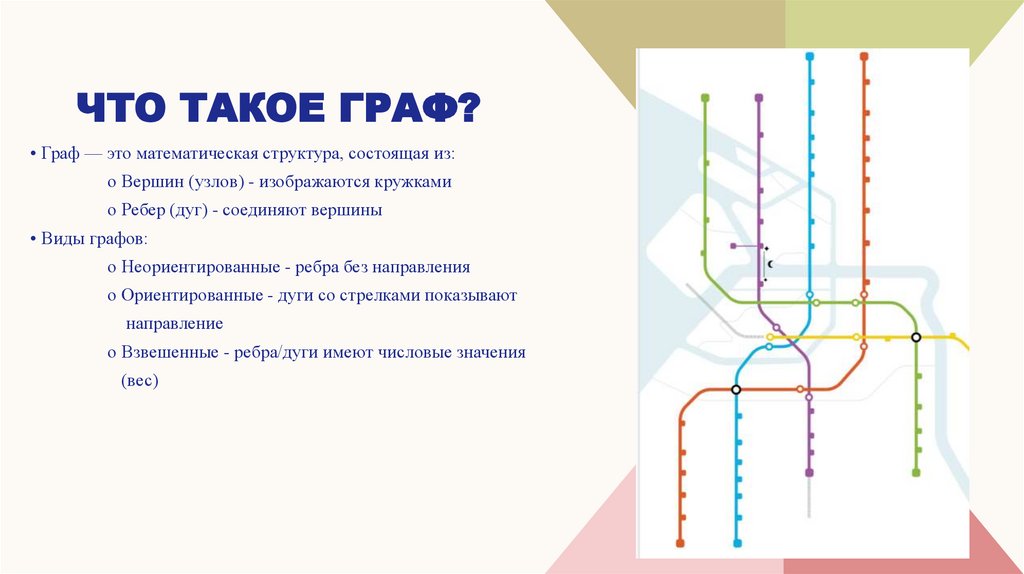
2
ЧТО ТАКОЕ ГРАФ?
• Граф — это математическая структура, состоящая из:
o Вершин (узлов) - изображаются кружками
o Ребер (дуг) - соединяют вершины
• Виды графов:
o Неориентированные - ребра без направления
o Ориентированные - дуги со стрелками показывают
направление
o Взвешенные - ребра/дуги имеют числовые значения
(вес)

3. Взвешенный граф и весовая матрица. Взвешенный граф – это граф, каждому ребру (дуге) которого поставлено в соответствие

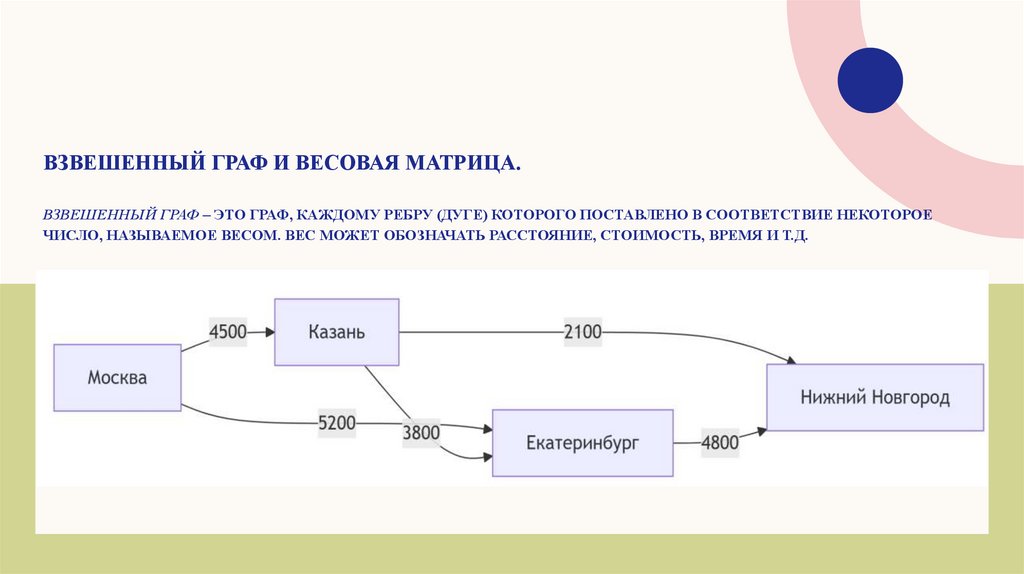
ВЗВЕШЕННЫЙ ГРАФ И ВЕСОВАЯ МАТРИЦА.
ВЗВЕШЕННЫЙ ГРАФ – ЭТО ГРАФ, КАЖДОМУ РЕБРУ (ДУГЕ) КОТОРОГО ПОСТАВЛЕНО В СООТВЕТСТВИЕ НЕКОТОРОЕ
ЧИСЛО, НАЗЫВАЕМОЕ ВЕСОМ. ВЕС МОЖЕТ ОБОЗНАЧАТЬ РАССТОЯНИЕ, СТОИМОСТЬ, ВРЕМЯ И Т.Д.

4. Весовая матрица – это матрица, на пересечении i-й строки и j-го столбца которой стоит вес дуги, ведущей из вершины i в вершину

ВЕСОВАЯ МАТРИЦА – ЭТО МАТРИЦА, НА ПЕРЕСЕЧЕНИИ I-Й СТРОКИ И J-ГО СТОЛБЦА
КОТОРОЙ СТОИТ ВЕС ДУГИ, ВЕДУЩЕЙ ИЗ ВЕРШИНЫ I В ВЕРШИНУ J. ЕСЛИ ДУГИ НЕТ, В
ЯЧЕЙКЕ СТАВИТСЯ СИМВОЛ «∞» (БЕСКОНЕЧНОСТЬ) ИЛИ В ПРАКТИЧЕСКИХ ЗАДАЧАХ,
ПРОЧЕРК.
Вершины
1
2
3
1
-
4500
5200
-
2
-
-
3800
2100
3
-
-
-
4800
4
-
-
-
-
4

5. Длина пути

ДЛИНА ПУТИ
Длина пути между вершинами графа.
Длина пути во взвешенном графе – это сумма весов всех
дуг, входящих в этот путь.
Если граф невзвешенный, длина пути равна количеству
ребер в нем.
Кратчайший путь – путь с минимальной длиной.
Пример: Найдите длину пути Москва -> Казань -> Нижний
Новгород.
Решение: 4500 + 2100 = 6600 рублей.

6. Ориентированный Ациклический Граф - ОАГ

6
ОРИЕНТИРОВАННЫЙ
АЦИКЛИЧЕСКИЙ ГРАФ - ОАГ
Вычисление количества путей в направленном ациклическом графе
(DAG).
Ориентированный ациклический граф (ОАГ) – это ориентированный граф, в
котором отсутствуют циклы (невозможно, выйдя из некоторой вершины, пройдя
по нескольким дугам, вернуться в нее же).
ОАГ идеально подходит для представления процессов, идущих в одном
направлении (например, этапы проекта, учебный план).
Метод подсчета путей: используется алгоритм динамического
программирования. Количество путей в вершину X равно сумме количеств
путей во все вершины, из которых ведут дуги в X. Для стартовой вершины
количество путей равно 1.

7. Схема обязательных курсов в учебном плане старшей школы (последовательность изучения).

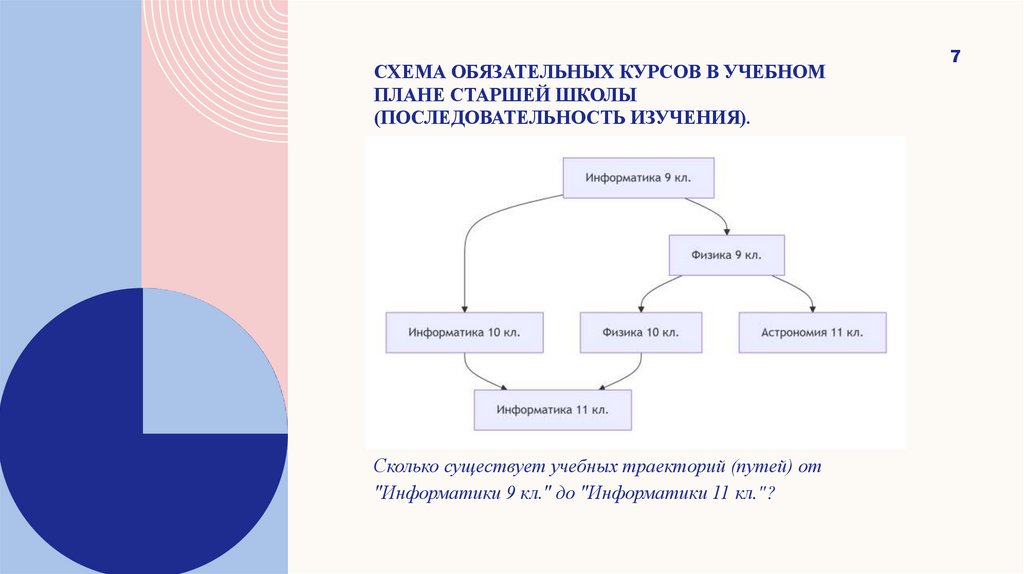
СХЕМА ОБЯЗАТЕЛЬНЫХ КУРСОВ В УЧЕБНОМ
ПЛАНЕ СТАРШЕЙ ШКОЛЫ
(ПОСЛЕДОВАТЕЛЬНОСТЬ ИЗУЧЕНИЯ).
Сколько существует учебных траекторий (путей) от
"Информатики 9 кл." до "Информатики 11 кл."?
7

8. Задача 1 (Базовый уровень)

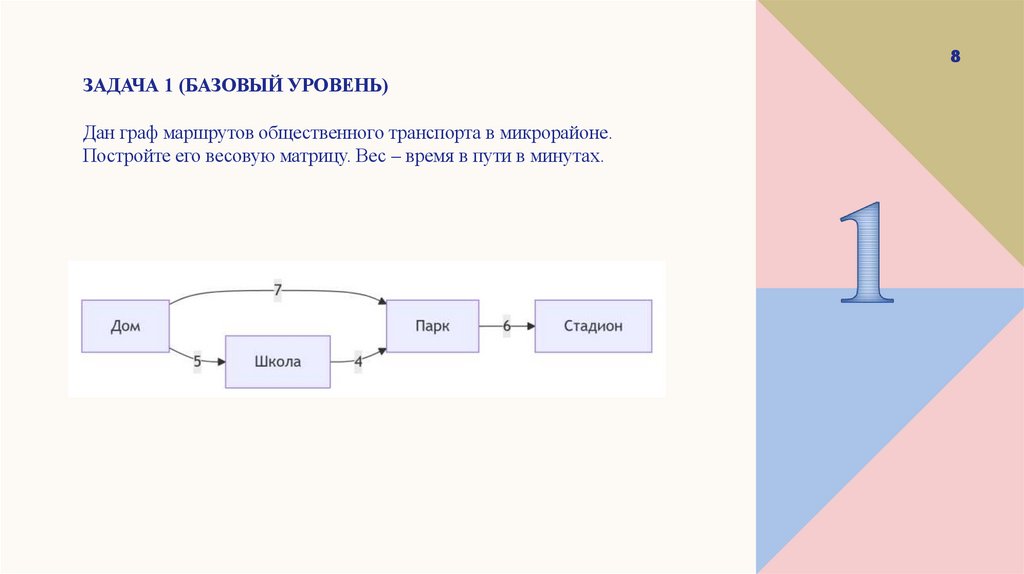
8
ЗАДАЧА 1 (БАЗОВЫЙ УРОВЕНЬ)
Дан граф маршрутов общественного транспорта в микрорайоне.
Постройте его весовую матрицу. Вес – время в пути в минутах.

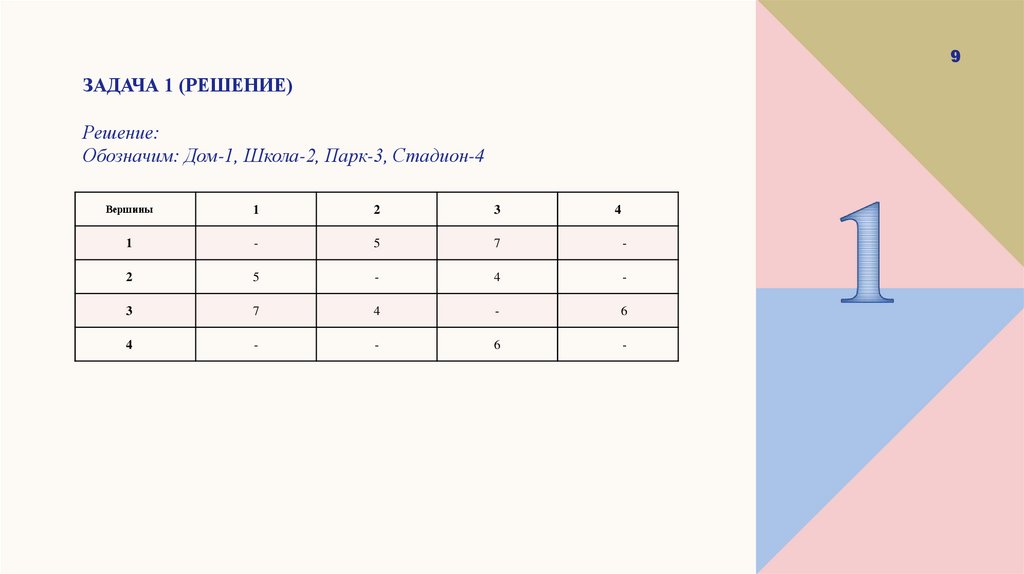
9. Задача 1 (РЕШЕНИЕ)

9
ЗАДАЧА 1 (РЕШЕНИЕ)
Решение:
Обозначим: Дом-1, Школа-2, Парк-3, Стадион-4
Вершины
1
2
3
1
-
5
7
-
2
5
-
4
-
3
7
4
-
6
4
-
-
6
-
4

10. Задача 2 (Базовый уровень)

10
ЗАДАЧА 2 (БАЗОВЫЙ УРОВЕНЬ)
По данной весовой матрице графа (вершины: 1,2,3,4) определите
длину пути из вершины 1 в вершину 4 по маршруту 1->3->4.
Вершины
1
2
3
1
-
10
15
-
2
-
-
5
20
3
-
-
-
12
4
-
-
-
-
4

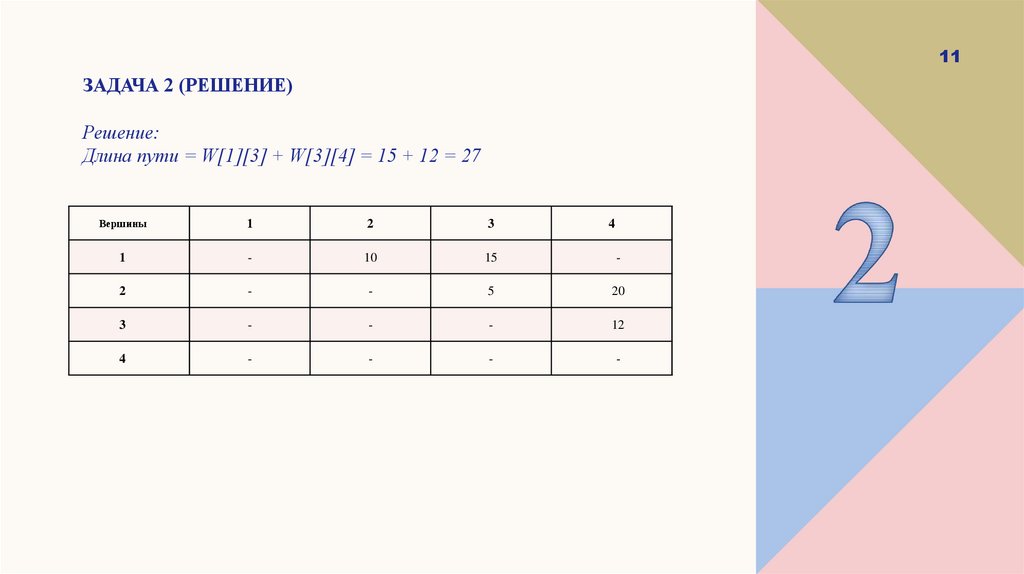
11. Задача 2 (РЕШЕНИЕ)

11
ЗАДАЧА 2 (РЕШЕНИЕ)
Решение:
Длина пути = W[1][3] + W[3][4] = 15 + 12 = 27
Вершины
1
2
3
1
-
10
15
-
2
-
-
5
20
3
-
-
-
12
4
-
-
-
-
4

12. Задача 3 (Повышенный уровень)

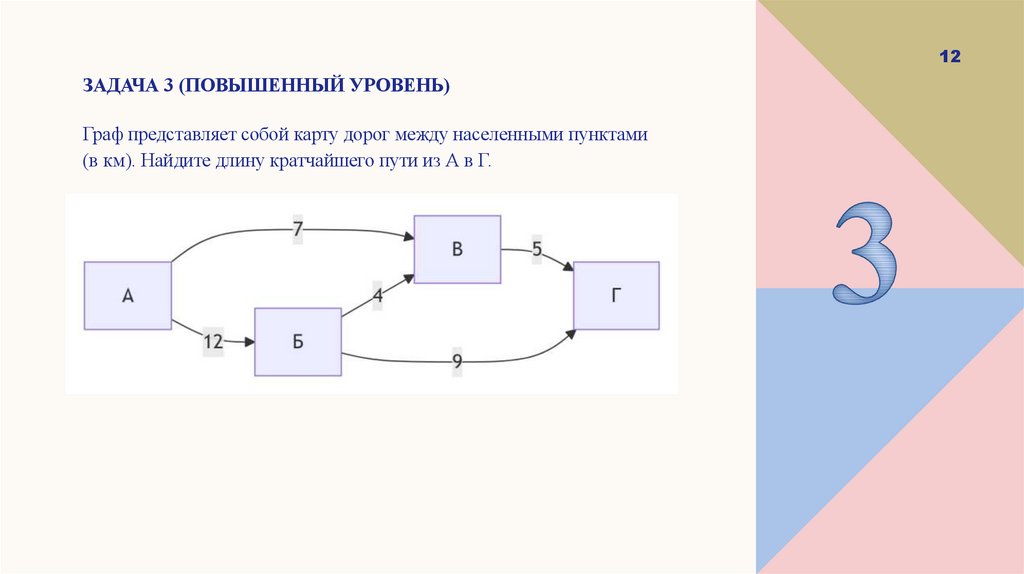
12
ЗАДАЧА 3 (ПОВЫШЕННЫЙ УРОВЕНЬ)
Граф представляет собой карту дорог между населенными пунктами
(в км). Найдите длину кратчайшего пути из А в Г.

13. Задача 3 (РЕШЕНИЕ)

13
ЗАДАЧА 3 (РЕШЕНИЕ)
Решение:
Рассмотрим все возможные пути из А в Г:
А→Б→Г: 12 + 9 = 21 км
А→В→Г: 7 + 5 = 12 км
• А→Б→В→Г: 12 + 4 + 5 = 21 км
Кратчайший путь: А→В→Г = 12 км

14. Задача 4 (Высокий уровень)

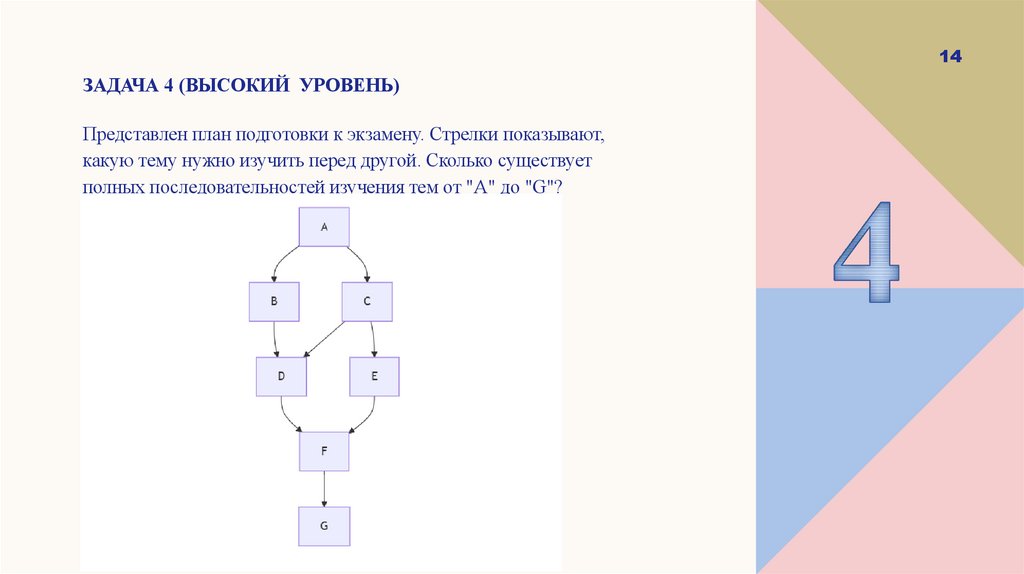
14
ЗАДАЧА 4 (ВЫСОКИЙ УРОВЕНЬ)
Представлен план подготовки к экзамену. Стрелки показывают,
какую тему нужно изучить перед другой. Сколько существует
полных последовательностей изучения тем от "А" до "G"?

15. Задача 4 (РЕШЕНИЕ)

15
ЗАДАЧА 4 (РЕШЕНИЕ)
Решение:
A: 1
B: A→B = 1
C: A→C = 1
D: B→D (1) + C→D (1) = 2
E: C→E = 1
F: D→F (2) + E→F (1) = 3
G: F→G = 3
Ответ: 3 полных последовательности

16. Задача 5 (Творческий уровень)

16
ЗАДАЧА 5 (ТВОРЧЕСКИЙ УРОВЕНЬ)
Придумайте реальную ситуацию из жизни вашего города/региона,
которую можно представить в виде взвешенного ориентированного
графа. Опишите, что будут обозначать вершины, дуги и вес.

17. Ключевые свойства весовой матрицы в ориентированных графах

КЛЮЧЕВЫЕ СВОЙСТВА
ВЕСОВОЙ МАТРИЦЫ В
ОРИЕНТИРОВАННЫХ ГРАФАХ
Весовая матрица
ориентированного графа, как
правило, несимметрична: веса
ребёр i→j и j→i могут сильно
различаться.
Отсутствие ребра между
вершинами обозначается
бесконечностью или прочерком,
что указывает на невозможность
прямого перехода.
Матрица является основным
инструментом для проведения
численных вычислений, таких
как поиск кратчайших путей и
оценки стоимости марафонов.
Использование весовой матрицы
упрощает алгоритмизацию и
структурированный анализ
сложных графов в инженерных и
научных задачах.
17

18. Практические аспекты применения графов и матриц

18
ПРАКТИЧЕСКИЕ АСПЕКТЫ
ПРИМЕНЕНИЯ ГРАФОВ И МАТРИЦ
Графы широко применяются в логистике для
оптимизации маршрутов доставки, что значительно
сокращает время и затраты на перевозки.
Весовые матрицы облегчают решение задач
планирования проектов, позволяя точно учитывать
временные ограничения и зависимости между
этапами.
В информационных технологиях графовые модели
помогают структурировать данные и управлять
сетевыми связями.

19. Значимость изучения графов и их матриц

ЗНАЧИМОСТЬ ИЗУЧЕНИЯ ГРАФОВ И
ИХ МАТРИЦ
Понимание графов и весовых матриц открывает
возможности для решения сложных задач
оптимизации, планирования и анализа, что важно
для науки, техники и образования.