Похожие презентации:
ДС_Л.6_Предельные циклы
1. Двумерные динамические системы
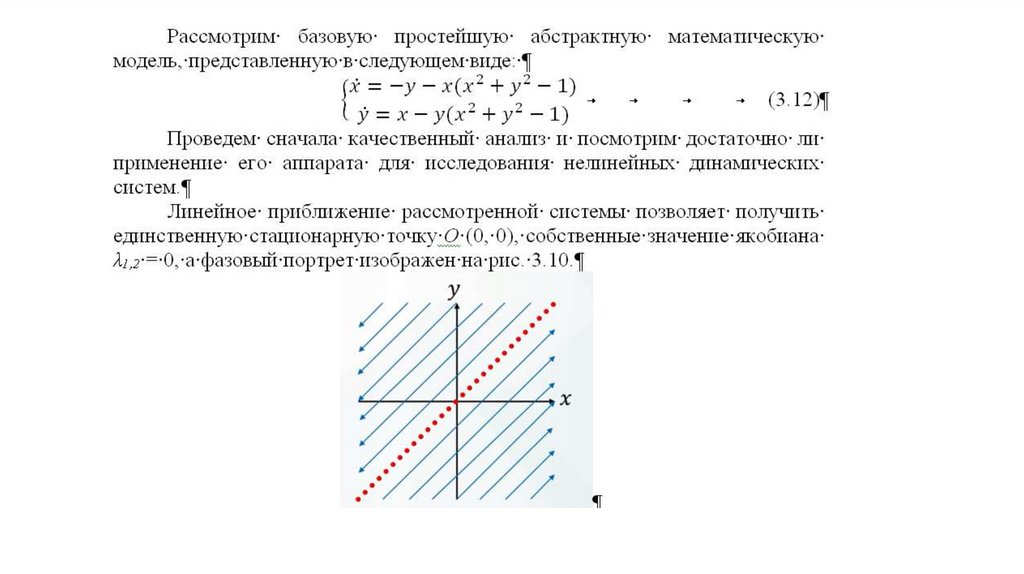
2. Простейшая математическая модель предельного цикла
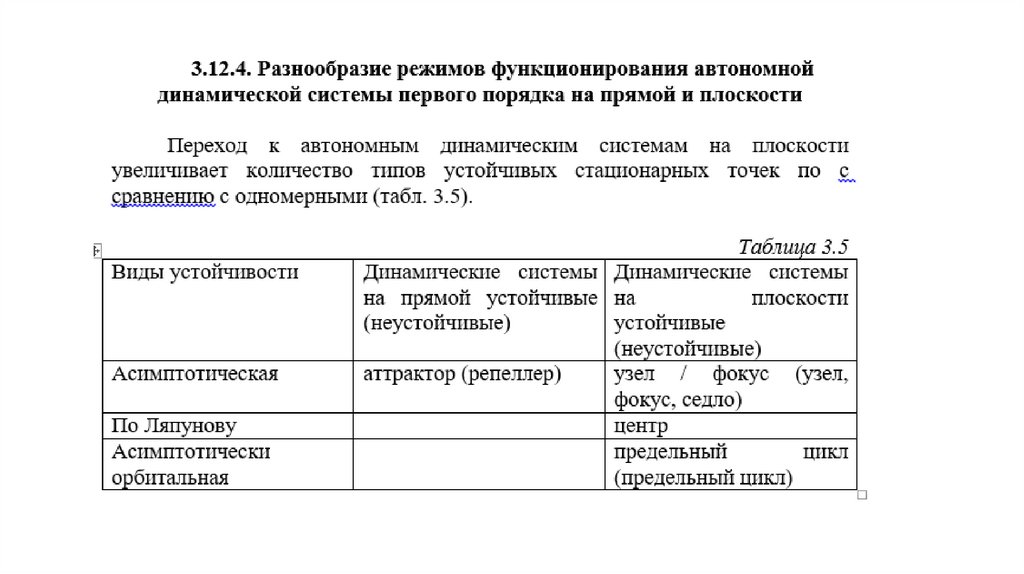
• При исследовании динамических систем на прямой могут возникнуть толькодве стационарные точки – аттракторы и репеллеры.
• При увеличении размерности пространства количество типов стационарных
точек увеличивается.
• Для нелинейных динамических систем на плоскости могу появится самые
разные стационарные точки, режимы, виды устойчивости.
• Ранее были рассмотрены асимптотические виды устойчивости – фокус или
спиральный узел, узел, центр которые нам дает линейное приближение.
• Этим не ограничивается многообразие режимов нелинейных динамических
систем.
• Существует еще один интересный режим или точка, возникающий только в
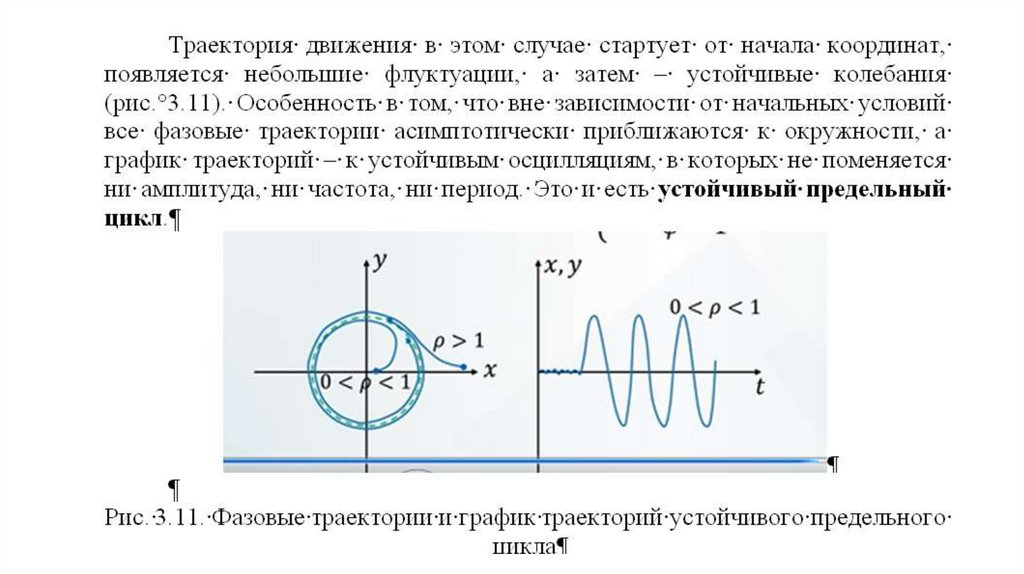
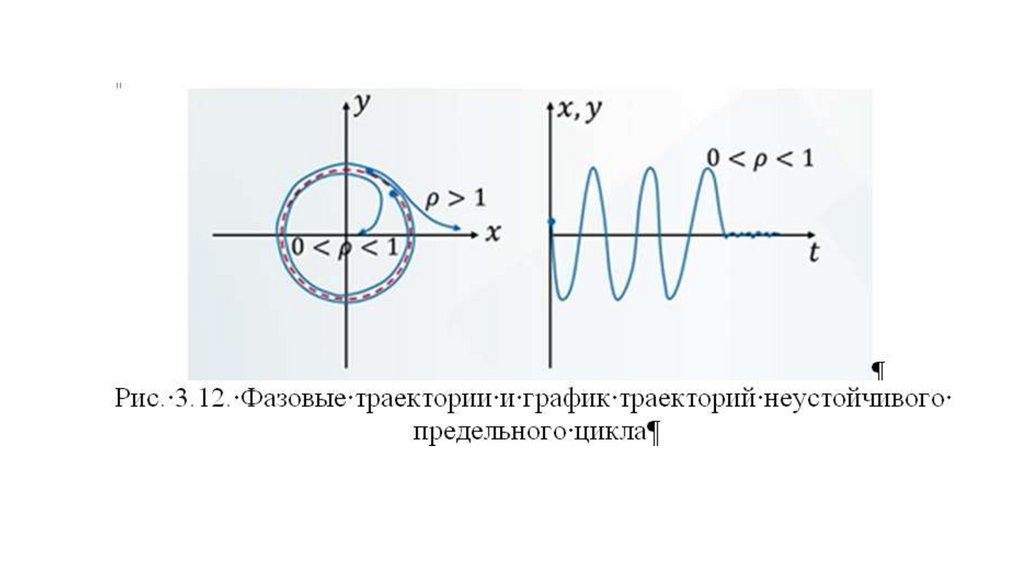
автономных динамических системах на плоскости – устойчивые и
неустойчивые предельные циклы.
3.
4.
5.
6.
7.
8.
9. Асимптотическая орбитальная устойчивость
10.
11.
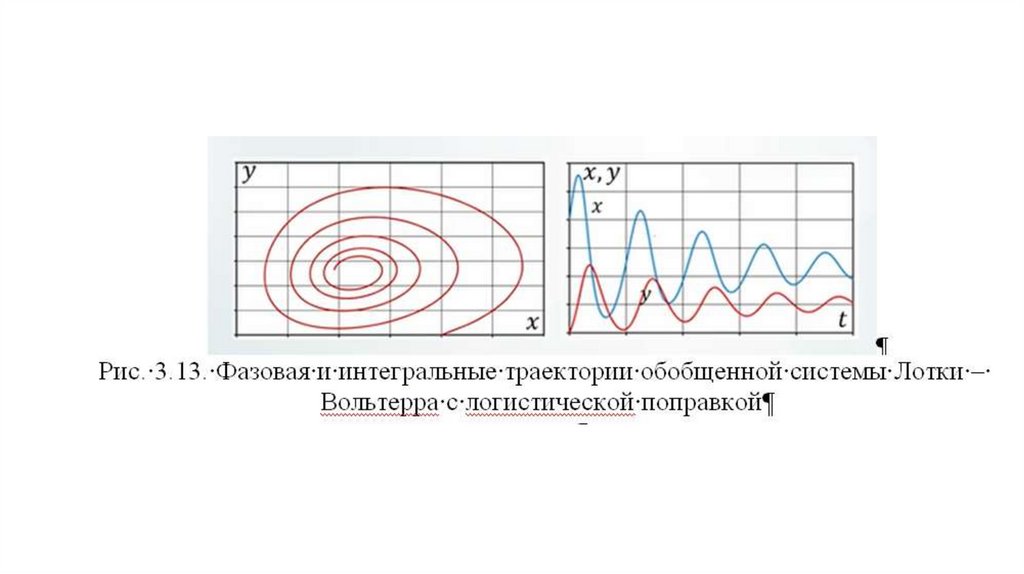
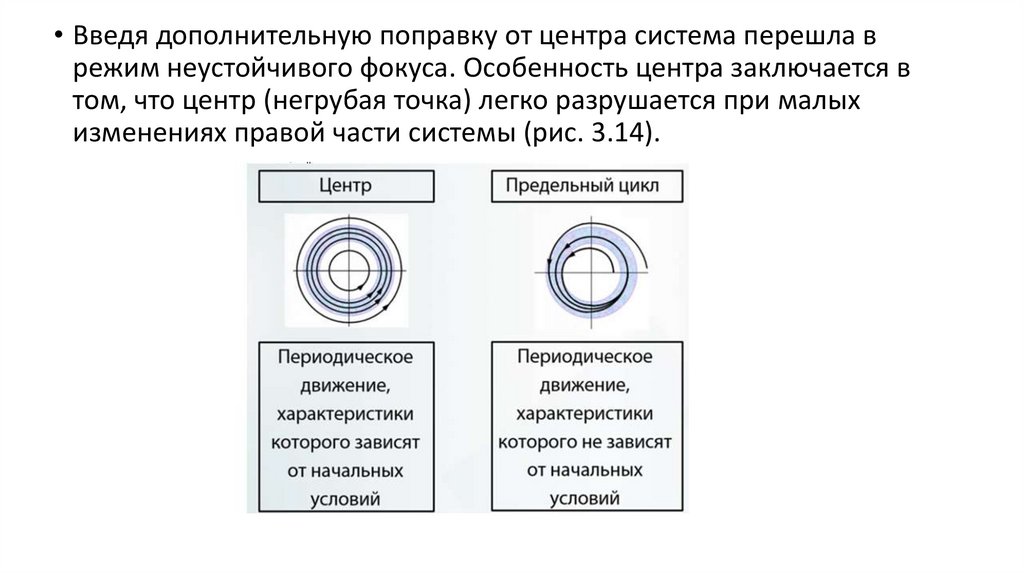
• Введя дополнительную поправку от центра система перешла врежим неустойчивого фокуса. Особенность центра заключается в
том, что центр (негрубая точка) легко разрушается при малых
изменениях правой части системы (рис. 3.14).