Litvinova_-_TETs_-_MUP

1. Метод узловых потенциалов

ФГБОУ ВО РГРТУ
Литвинова В. С.
Метод
узловых потенциалов
Методические указания
к самостоятельной работе
Рязань 2025

2. Оглавление

1
УДК 621.3.011.714
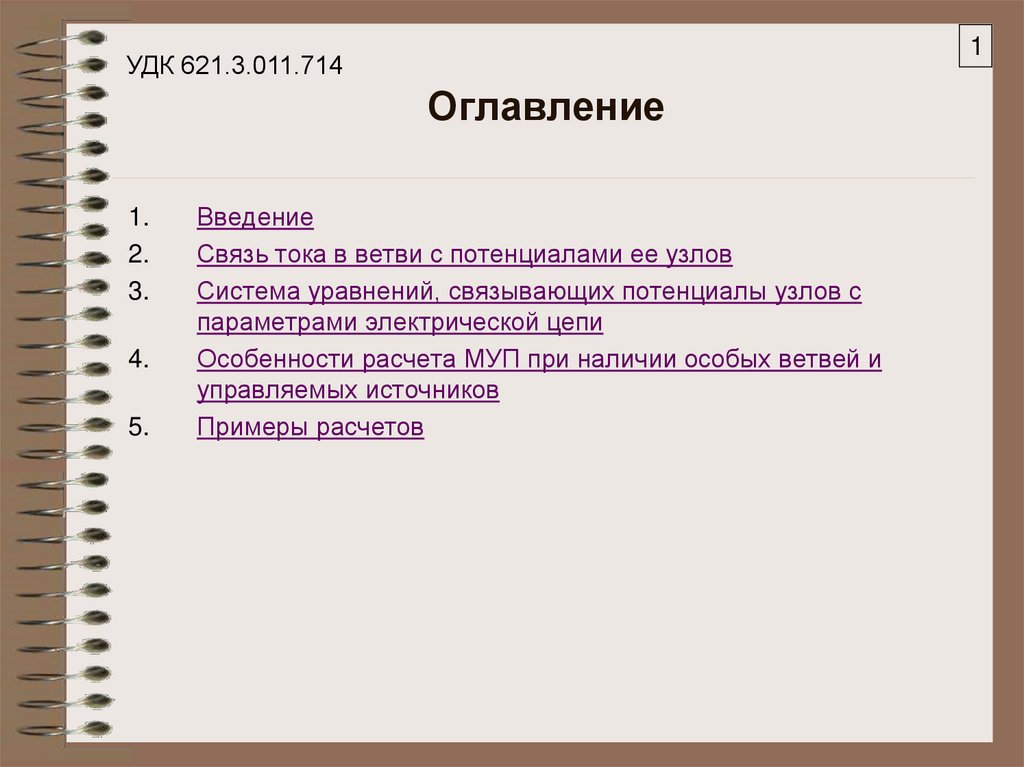
Оглавление
1.
2.
3.
4.
5.
Введение
Связь тока в ветви с потенциалами ее узлов
Система уравнений, связывающих потенциалы узлов с
параметрами электрической цепи
Особенности расчета МУП при наличии особых ветвей и
управляемых источников
Примеры расчетов

3. 1. Введение

2
1. Введение
Сущность метода узловых потенциалов (МУП) состоит в
составлении и решении системы уравнений, связывающих
потенциалы узлов с параметрами электрической цепи. По
полученным потенциалам узлов рассчитывают токи ветвей схемы.
МУП является универсальным и эффективным методом расчета
режима в сложных электрических цепях. Из-за простоты описания
этот метод положен в основу машинного анализа электронных схем.
[Назад] [Оглавление] [Дальше]

4. 2. Связь тока в ветви с потенциалами ее узлов

3
2. Связь тока в ветви с потенциалами ее узлов
Выясним правила расчета токов в ветвях сложной цепи по известным потенциалам
узлов. Рассмотрим примеры.
Пример 1. Найти ток в k-й ветви, содержащей резистор, подключенный к узлам а и b
(рис. 1) электрической цепи, если известны потенциалы узлов ( a, b) и сопротивление
резистора Rk.
Выберем направление тока Ik, например, от узла a к узлу b: Ik = Iab , и поэтому будем
считать, что потенциал точки a больше потенциала точки b (известно, что ток течет из
точки с большим потенциалом в точку с меньшим потенциалом).
В таком же порядке возьмем и направление отсчета напряжения Uk = Uab = a - b.
Тогда по закону Ома:
I k I ab
U ab a b
Rk
Rk
(1)
Рис. 1
[Назад] [Оглавление] [Дальше]

5.

4
Пример 2. Найти ток в k-й ветви, подключенной к узлам a и b (рис. 2), содержащей
резистор и источник э. д. с., если известны потенциалы узлов ( a , b ), сопротивление
резистора Rk и э. д. с. Еk.
Рис. 2
Выберем направление тока Ik, например, от узла a к узлу b, Ik = Iab. В таком же
порядке возьмем и направление отсчета напряжения Uk = Uab = a - b. Выразим
искомый ток Ik из уравнения по второму закону Кирхгофа для контура (a, Rk , c, Еk , b, a):
I ab Rk U ab Ek I k I ab
U ab Ek a b Ek
Rk
Rk
(2)
Заметим, что э. д. с. Еk совпадает по направлению с током Iab и записана в
числителе выражения (2) со знаком (+). Если бы э. д. с. Еk , была направлена против
тока, то она была бы записана со знаком (-). С учетом этого замечания соотношение
между током ветви Iab и потенциалами узлов a , b имеет вид:
I k I ab
a b Ek
(3)
Rk
Полученную формулу (3) называют также обобщенным законом Ома.
[Назад] [Оглавление] [Дальше]

6. 3. Система уравнений, связывающих потенциалы узлов с параметрами электрической цепи

5
3. Система уравнений, связывающих потенциалы
узлов с параметрами электрической цепи
Выясним структуру и алгоритм формирования системы уравнений, связывающих
потенциалы узлов с параметрами схемы, на примере произвольно выбранного узла
(рис. 3) сложной цепи с nу узлами.
Присвоим базовому узлу нулевой номер и нулевой
потенциал 0 = 0. Число искомых потенциалов равно
числу независимых узлов n = nу - 1.
Для рассматриваемого 1-го узла запишем уравнение
по первому закону Кирхгофа:
Il - I2 - I3 + I4 - J5 - I6 = 0.
Умножим его на -1 и укажем индексами полярность
токов:
-I21 + I12 + I13 - I31 + J5 + I10 = 0.
Выразим токи через потенциалы узлов по закону
Ома (3):
2 1 E1 1 2 E2 1 3 E3 3 1
J5 1 0 0
R1
R2 R2
R3
R4
R6
Сгруппировав подобные, получим уравнение для
первого узла по (МУП):
Рис. 3
1
1
R1
1
1
E3
E1
E2
1
1
1
1
1
1
2
J 5 (4)
3
R R R
R2 R2 R3 R4 R6
R
R
R
R
R
R
1
2
2
3
4
1
2
2
3
[Назад] [Оглавление] [Дальше]

7.

6
Закономерности структуры уравнения узла.
1
2.
3.
В левой части уравнения потенциал рассматриваемого узла умножается на
узловую проводимость, равную сумме проводимостей всех ветвей, сходящихся в
этом узле и записывается со знаком «+».
В данном примере (рис. 3) проводимость пятой ветви равна нулю, т. к. внутреннее
сопротивление идеального источника тока равно .
Остальные слагаемые в левой части записывают со знаком « » и представляют
собой произведение потенциалов смежных узлов на смежную проводимость,
равную сумме проводимостей ветвей, соединяющих рассматриваемый узел со
смежным.
В правой части уравнения записывают узловые токи источников ветвей,
сходящихся в рассматриваемом узле.
Если источник э. д. с. направлен к рассматриваемому узлу, то узловой ток Ek /Rk
записывается со знаком «+». Если источник э. д. с. направлен от рассматриваемого
узла, то узловой ток Ek /Rk записывается со знаком « ».
Аналогичное правило знаков распространяется на источники тока.
Порядок расчета токов МУП.
1.
2.
3.
4.
Анализ схемы. Разметка узлов, ветвей и токов в них. Базовому узлу присваивают
нулевой номер и нулевой потенциал.
Запись системы уравнений МУП согласно установленным закономерностям.
Подстановка исходных числовых данных, формирование и решение расширенной
матрицы системы. Расчет потенциалов узлов схемы.
Расчет токов ветвей по полученным потенциалам.
Проверка токов.
[Назад] [Оглавление] [Дальше]

8.

7
Исходя из указанных закономерностей запишем систему уравнений МУП в общем
виде для электрической цепи с n = nу 1 независимыми узлами.
0 = 0
Коэффициенты
с
одинаковыми
1G11 2G12 k G1k nG1n J y1
индексами
вида
G
,
G
,
G
,
G G G G J
11
22
kk Gnn означают
1
21
2
22
k
2
k
n
2
n
y
2
узловые проводимости соответствующих
узлов.
1Gk1 2Gk 2 k Gkk nGkn J yk
1Gn1 2Gn 2 k Gnk nGnn J yn
Система уравнений МУП в матричной форме:
G11 G12 G1k G1n 1 J y1
G21 G22 G2 k G2 n 2 J y 2
Gk1 Gk 2 Gkk Gkn k J yk
G G G G J
nk
nn
n
n1 n 2
yn
Коэффициенты с разными индексами
вида
Gkm означают взятую со знаком
« »
смежную проводимость между
узлами k и m.
В правой части свободные члены вида Jyk
означают узловой ток k-го узла
k
k
Ei
J yk
Ji
R
i 1 i
i 1
равный сумме узловых токов источников
ветвей, сходящихся в k-ом узле.
Заметим, что матрица узловых проводимостей линейной цепи симметрична
относительно главной диагонали, т. к. Gkm = Gmk , что является критерием правильности
полученной системы уравнений МУП.
[Назад] [Оглавление] [Дальше]

9. 4. Особенности расчета МУП при наличии особых ветвей и управляемых источников

8
4. Особенности расчета МУП при наличии
особых ветвей и управляемых источников
Особой называют ветвь, не содержащую сопротивления. К таковым относятся ветви с
источником э. д. с. без сопротивления и обычные закоротки. Наличие особой ветви в
схеме приводит к появлению в уравнениях по МУП бесконечности и к сбою в
решении. Эту трудность устраняют следующими способами:
1 способ. Если в схеме особые ветви имеют общий узел (рис. 4), то этот узел выбирают
базовым, ему присваивают нулевой номер и нулевой потенциал; потенциалы других
узлов особых ветвей становятся известными: а = Eа , b = 0, с = Eс .
Токи в особых ветвях вычисляются по первому закону Кирхгофа на основе
остальных токов, рассчитанных по потенциалам узлов схемы.
2 способ. Если в схеме особые ветви не имеют общего узла (рис. 5), то потенциалы
узлов особых ветвей ( a , b , с , d) неизвестны и появление бесконечности в
уравнениях сохраняется.
Рис. 4
Рис. 5
[Назад] [Оглавление] [Дальше]

10.

9
В способе 2 особые ветви представляют источниками тока с неизвестными токами IOV ,
что снимает проблему бесконечности в уравнениях, но увеличивает число искомых
неизвестных на число особых ветвей NOV (cм. ПРИЛОЖЕНИЕ).
В этом способе сохраняются неизменными и схема и правила формирования
основных уравнений системы. К достоинству метода можно отнести и то, что кроме
искомых потенциалов одновременно получают токи особых ветвей.
При наличии в схеме управляемых источников метод формирования основных
уравнений МУП сохраняется, но основных уравнениях появляются дополнительные
неизвестные управляющие величины. Поэтому возникает необходимость в
дополнительных уравнениях, связывающих управляющую величину с потенциалами
узлов.
[Назад] [Оглавление] [Дальше]

11.

10
5. Примеры расчетов
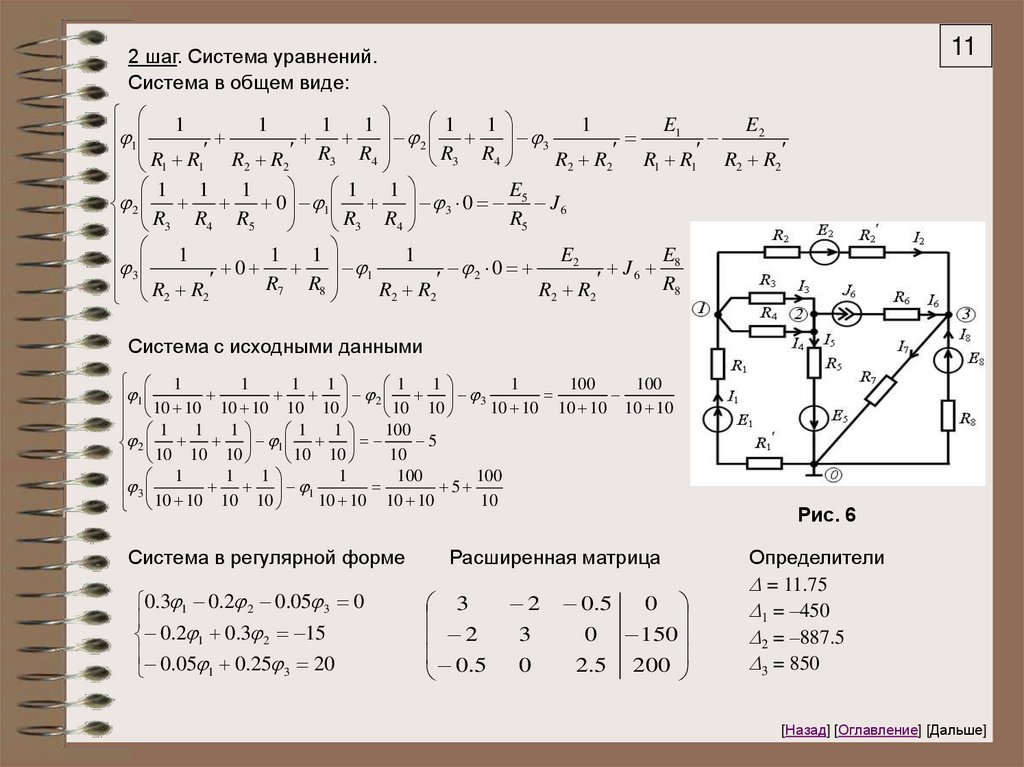
Пример 1. Рассчитать токи в цепи, схема которой изображена на рис. 6.
Сопротивления резисторов одинаковы (по 10 Ом), э. д. с. одинаковы (по 100 В), источник
тока J6 = 5 A.
Решение.
1 шаг. Анализ схемы. Разметка узлов, ветвей и
токов в них.
Схема содержит:
- ветвей nв = 7, узлов nу = 4,
- независимых узлов n = nу – 1 = 4 – 1 = 3,
- зависимый (базовый) узел с нулевым номером и
потенциалом 0 = 0,
- независимых потенциалов n = 3,
- независимых уравнений по МУП nур = n = 3.
Рис. 6
[Назад] [Оглавление] [Дальше]

12.

11
2 шаг. Система уравнений.
Система в общем виде:
1
1
1
1
1
1
1
E1
E2
1
2 3
R1 R1 R2 R2 R3 R4
R3 R4
R2 R2
R1 R1 R2 R2
1
E
1
1
1
1
0 1 3 0 5 J 6
2
R5
R3 R4
R3 R4 R5
E
1
1
1
1
E2
3
0
1
2 0
J6 8
R7 R8
R8
R2 R2
R2 R2
R2 R2
Система с исходными данными
1
1
1
1
1
1
100
100
1
2 3
1
10 10 10 10 10 10
10 10
10 10 10 10 10 10
1
1
1
100
1
1
5
2 1
10
10 10
10 10 10
1
1
1
100
100
1
3 10 10 10 10 1 10 10 10 10 5 10
Система в регулярной форме
0.3 1 0.2 2 0.05 3 0
0.2 1 0.3 2 15
0.05 0.25 20
1
3
Расширенная матрица
3
2
0.5
2
3
0
0 150
2.5 200
0.5
0
Рис. 6
Определители
= 11.75
1 = –450
2 = –887.5
3 = 850
[Назад] [Оглавление] [Дальше]

13.

12
Потенциалы:
0 = 0
1 = 1 / = – 450 / 11.75 = – 38.298 В
2 = 2 / = – 887.5 / 11.75 = – 75.532 В
3 = 3 / = 850 / 11.75 = 72.340 В
3 шаг. Расчет токов.
0 1 E1
0 ( 38 .298 ) 100
6.915 A
10 10
1 3 E2
38 .298 72 .340 100
0.5319 A
10 10
I1 I 01
I 2 I13
R1 R1
I 3 I12
R2 R2
1 2
R2
38 .298 ( 75 .532 )
3.7234 A
10
I4 = I3 = 3.234 A
I 5 I 20
I 7 I 30
2 0 E5
R5
75 .532 0 100
2.4468 A
10
Рис. 6
3 0 72.340 0
7.2340 A
R7
10
I 8 I 03
0 3 E8
R8
0 72.340 100
6.915 A
10
[Назад] [Оглавление] [Дальше]

14.

13
4 шаг. Проверка токов.
Критерием правильности полученных токов является их соответствие законам
Кирхгофа, но основным из них для МУП является первый закон. По второму закону
Кирхгофа можно проверить лишь правильность вычисления токов по потенциалам
согласно (3)
a b Ek
I k I ab
Rk
но не самих потенциалов, т. к. соотношение (3) получено из уравнения по второму
закону Кирхгофа.
Для проверки токов следует брать базовый узел и такие, где больше ветвей. Важно,
чтобы все проверяемые токи были учтены в проверочных уравнениях. В
рассматриваемом примере 1 (рис.3) для проверки семи токов достаточно двух
уравнений:
для 0-го узла I5 + I7 = I1 + I8.
Л.ч. = I5 + I7 = 2.4468 + 7.234 = 9.6808 пр.ч. = I1 + I8 = 6.915 + 2.766 = 9.681 с погрешностью
9.6808 9.681
100 0.0021%,
9.6808
для 1-го узла I1 = I2 + I3 + I4.
Л.ч. = I1 = 6.915 пр.ч. = I2 + I3 + I4 = – 0.5319 + 3.7274 + 3.7274 =6.9229 с погрешностью
6.915 6.9229
100 0.11%,
6.915
Вывод. Полученные токи удовлетворяют первому закону Кирхгофа с погрешностью не
более 0.11%.
Ответ:
I1 = 6.915 А
I5 = 2.4468 А
I2 = – 0.5319 А
I6 = J6 = 5 A
I3 = 3.7234 А
I7 = 7.2340 A
I4 = 3.7234 А
I8 = 6.915 A
[Назад] [Оглавление] [Дальше]

15.

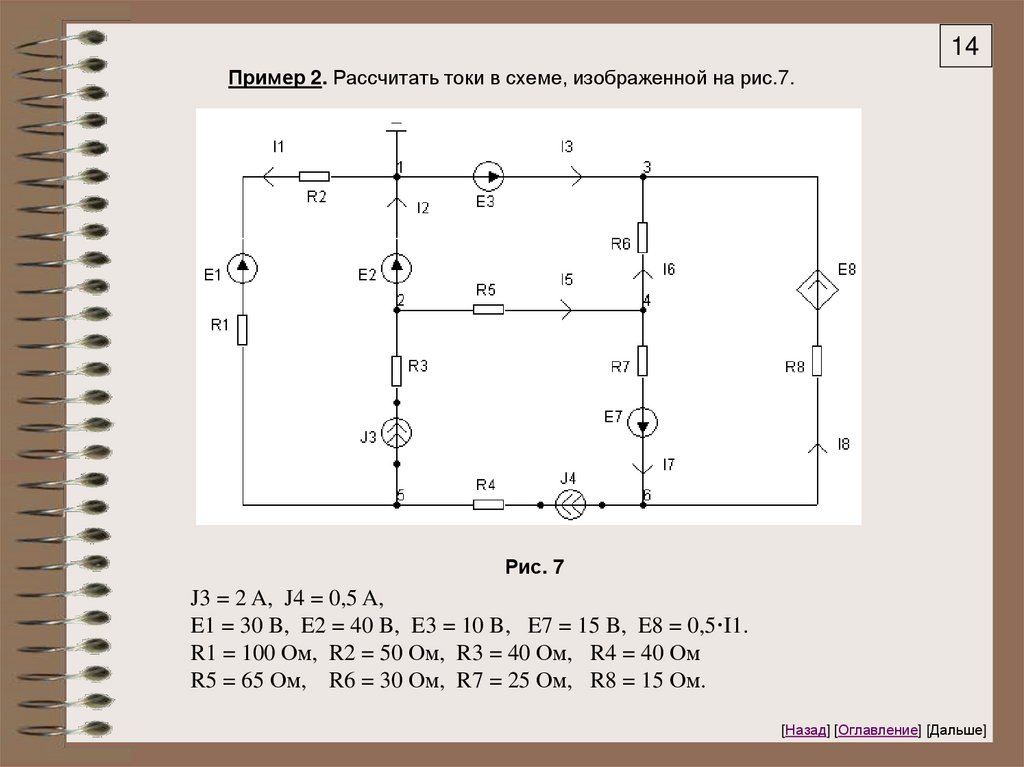
14
Пример 2. Рассчитать токи в схеме, изображенной на рис.7.
Рис. 7
J3 = 2 A, J4 = 0,5 A,
E1 = 30 B, E2 = 40 B, E3 = 10 B, E7 = 15 B, E8 = 0,5·I1.
R1 = 100 Ом, R2 = 50 Ом, R3 = 40 Ом, R4 = 40 Ом
R5 = 65 Ом, R6 = 30 Ом, R7 = 25 Ом, R8 = 15 Ом.
[Назад] [Оглавление] [Дальше]

16.

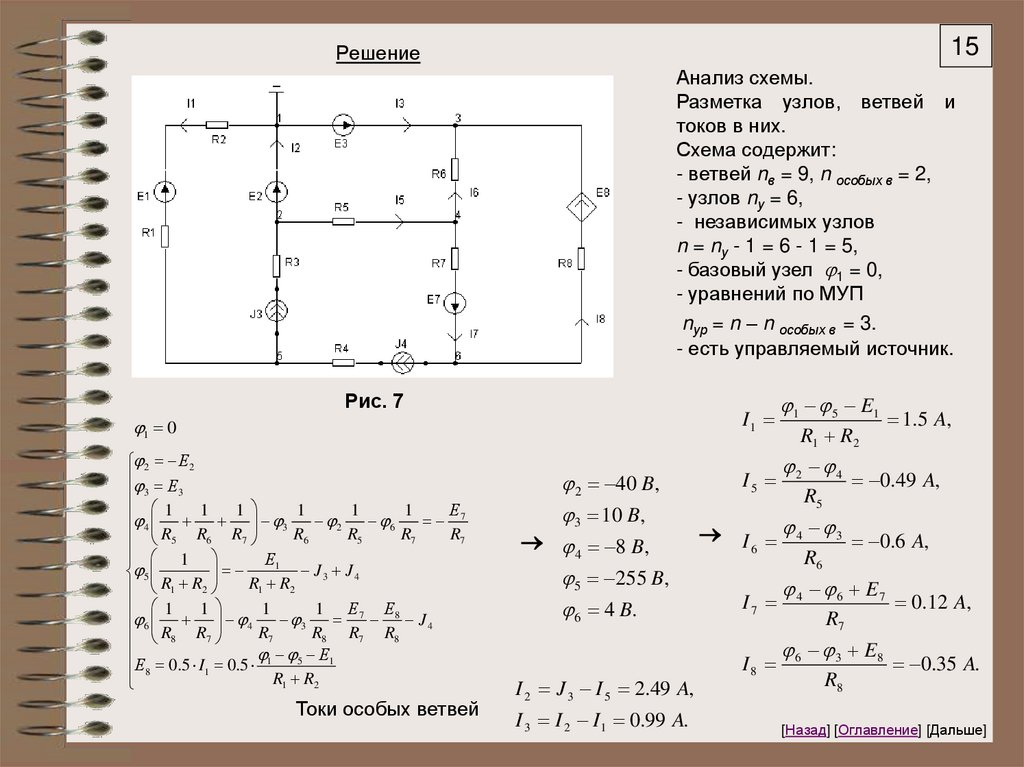
15
Решение
Анализ схемы.
Разметка узлов, ветвей и
токов в них.
Схема содержит:
- ветвей nв = 9, n особых в = 2,
- узлов nу = 6,
- независимых узлов
n = nу - 1 = 6 - 1 = 5,
- базовый узел 1 = 0,
- уравнений по МУП
nур = n – n особых в = 3.
- есть управляемый источник.
Рис. 7
I1
1 0
2 Е2
Е
3
3
Е7
1
1
1
1
1
1
4 R R R 3 R 2 R 6 R R
6
7
6
5
7
7
5
Е1
1
J3 J4
5
R1 R2
R1 R2
1
1
1
1 Е7 Е8
3
J4
6 4
R7
R8 R7 R8
R8 R7
1 5 Е1
Е8 0.5 I1 0.5 R R
1
2
Токи особых ветвей
2 40 B,
3 10 B,
4 8 B,
5 255 B,
6 4 B.
I 2 J 3 I 5 2.49 A,
I 3 I 2 I 1 0.99 A.
I5
1 5 E1
R1 R2
2 4
R5
1.5 A,
0.49 A,
I 4 3 0.6 A,
6
R6
I7
I8
4 6 E7
R7
6 3 E8
R8
0.12 A,
0.35 A.
[Назад] [Оглавление] [Дальше]

17.

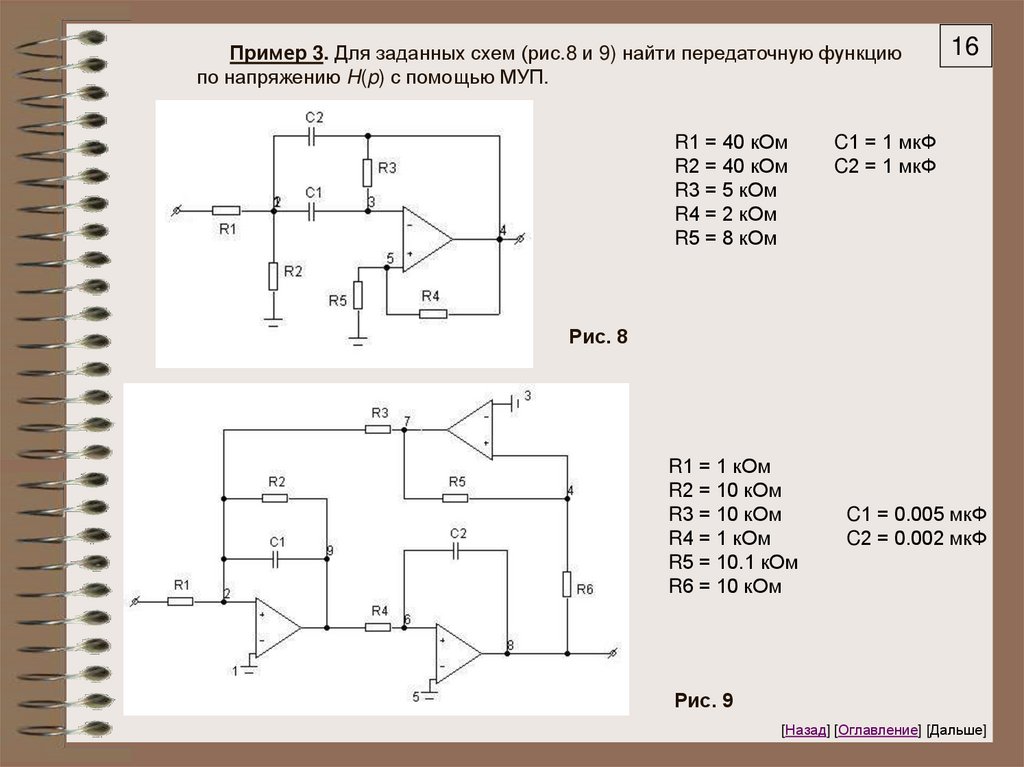
Пример 3. Для заданных схем (рис.8 и 9) найти передаточную функцию
по напряжению H(p) с помощью МУП.
R1 = 40 кОм
R2 = 40 кОм
R3 = 5 кОм
R4 = 2 кОм
R5 = 8 кОм
16
C1 = 1 мкФ
C2 = 1 мкФ
Рис. 8
R1 = 1 кОм
R2 = 10 кОм
R3 = 10 кОм
R4 = 1 кОм
R5 = 10.1 кОм
R6 = 10 кОм
C1 = 0.005 мкФ
C2 = 0.002 мкФ
Рис. 9
[Назад] [Оглавление] [Дальше]

18.

17
Операционный усилитель (ОУ), изображенный на схемах в виде рис. 10, при
расчетах рекомендуется представлять в виде схемы замещения (рис. 11), которая
соответствует идеальному
ОУ с бесконечно большим входным сопротивлением,
бесконечно малым выходным сопротивлением и бесконечно большим коэффициентом
усиления напряжения k во всем диапазоне частот.
U
Рис. 10
Рис. 11
Напряжение на выходе ОУ определяется формулой: Uвых = k( 1 - 2 ).
Так как выходное напряжение в реальных схемах – конечная величина, то разность
потенциалов 1 и 2 должна равняться нулю ( 1 = 2 ).
Передаточной функцией цепи H(p) называется отношение изображения выходной
величины к изображению входной величины.
[Назад] [Оглавление] [Дальше]

19.

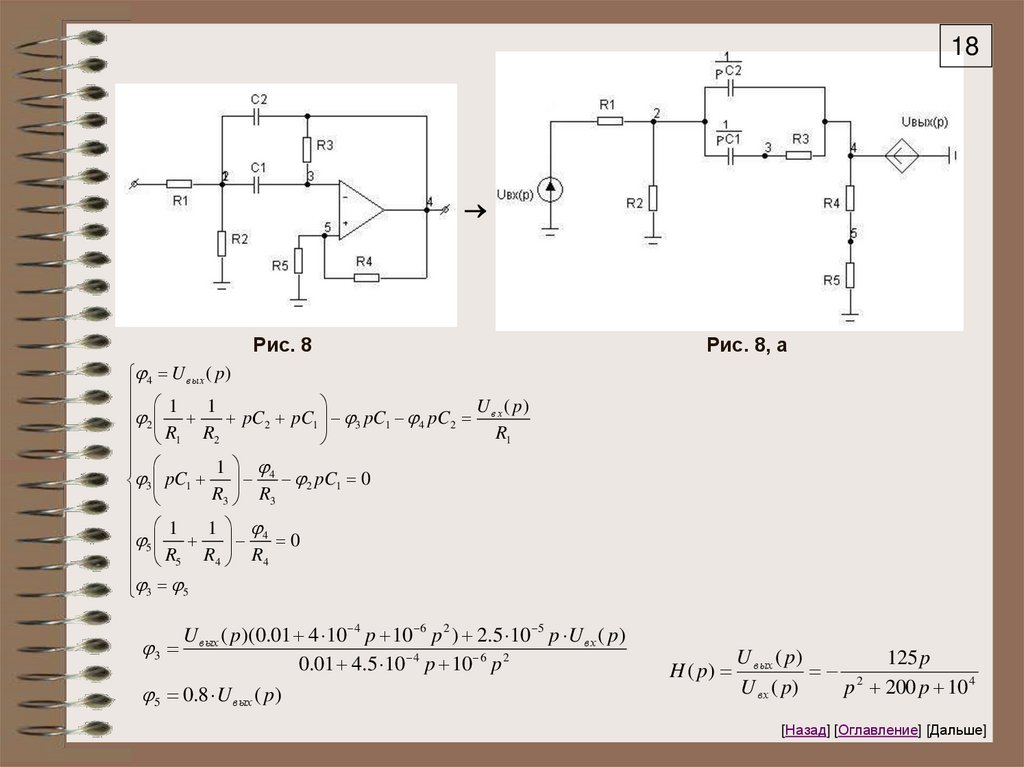
18
Рис. 8
Рис. 8, а
4 U в ых ( p )
1 1 pC pC pC pC U в х ( p )
2
1
3
1
4
2
2 R1 R2
R1
1 4
3 pC1 2 pC1 0
R3 R3
5 1 1 4 0
R5 R4 R4
3 5
U вых ( p)(0.01 4 10 4 p 10 6 p 2 ) 2.5 10 5 p U вх ( p)
0.01 4.5 10 4 p 10 6 p 2
5 0.8 U вых ( p)
3
H ( p)
U вых ( p)
125 p
2
U вх ( p)
p 200 p 10 4
[Назад] [Оглавление] [Дальше]

20.

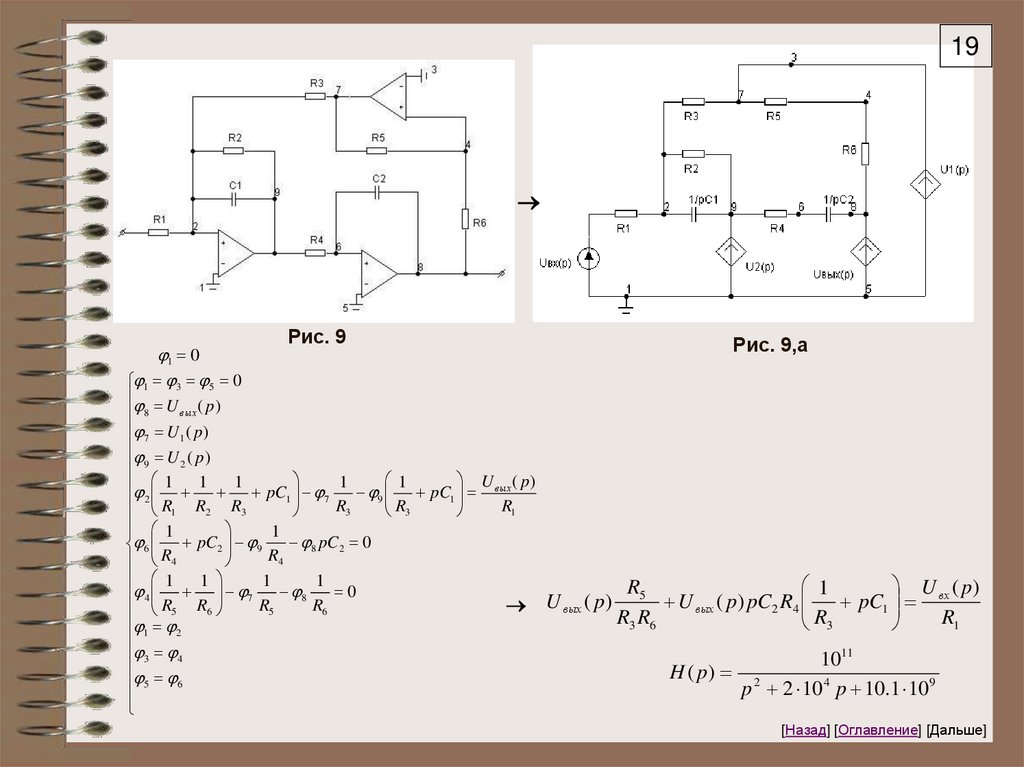
19
1 0
1 3 5 0
U ( p )
вых
8
7 U1 ( p )
9 U 2 ( p )
Рис. 9
Рис. 9,а
1
1
U ( p)
1
1
1
pC1 7
9 pC1 вых
2
R3
R1
R3
R1 R2 R3
1
1
8 pC2 0
6 pC2 9
R4
R4
1
1
1
1
1
U вх ( p)
R5
8
0
4 7
U
(
p
)
U
(
p
)
pC
R
pC
R
R
R
R
вых
вых
2
4
1
5
6
5
6
R
R
R
R1
3 6
3
1 2
3 4
1011
H ( p) 2
5 6
p 2 10 4 p 10.1 10 9
[Назад] [Оглавление] [Дальше]

21.

20
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
• 1. Немцов М.В., Немцова М.Л. Электротехника и электроника.
М: Академия, 2017 г.
• 2. Бессонов Л.А. Теоретические основы электротехники. М.:
Гардарики, 2007 г.
• 3. Попов В.П. Основы теории цепей. М.: Юрайт, 2023 г.
• 4. Демирчан К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л.
Теоретические основы электротехники. СПб.: Питер, 2003 г.