______ 4 ______ т.алгоритмы

1. САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Направление 15.03.04
Автоматизация технологических процессов и производств
Алгоритмическое обеспечение систем автоматизации и
управления
Направление 27.03.04
Управление в технических системах
Алгоритмическое обеспечение систем автоматизации и
управления
Куркина
Виктория Вадимовна

2.

Понятие достоверности
1 Достоверность - это характеристика знаний как
обоснованных, доказанных, истинных.
2 Достоверность – это свойство информации
отражать реально существующие объекты с необходимой
точностью.
Под
достоверностью
понимается
свойство
информации
давать
сведения
характеризующиеся
погрешностями,
не
выходящими
за
пределы
допустимых
2
значений.
3
4 Достоверность измерений – это показатель
степени доверия к результатам измерения, то есть
вероятность отклонений измерения от действительных
значений.

3.

Проблема повышения достоверности
Одной из наиболее актуальных проблем
организации автоматических систем управления
(АСУ)
является
обеспечение
достоверности
используемой в них измерительной информации.
Актуальность
быстрым
этой
ростом
проблемы
количества
3
обусловлена
разнообразных
объектов АСУ – на производстве, на транспорте, в
оборонной технике и даже в быту.

4.

Проблема повышения достоверности
Особенно
комплексы,
высокий
темп
управляемые
без
развития
отличает
непосредственного
участия человека, а также дистанционно, например,
"умные"
дома,
роботизированные
системы,
космические станции и т.д. Но каждая АСУ содержит
средства измерений (СИ), в том числе, датчики, а
поступающая
4
от
них
информация
процессы управления в системе.
определяет

5.

Проблема повышения достоверности
Недостоверная
резко
увеличивает
продукции,
оценкам,
аварий
она
измерительная
риск
и
возникновения
катастроф.
порождает
информация
до
60%
По
брака
некоторым
таких
событий.
Ситуация усугубляется тем, что традиционные методы
обеспечения
достоверности
измерительной
информации опираются на предположение, что при
регулярном
5
метрологическом
обслуживании
СИ,
предусматривающем их поверку или калибровку с
интервалом 1-2 года, вероятность выхода погрешности
измерений за допустимые границы достаточно мала.

6.

Проблема повышения достоверности
В действительности, по зарубежным данным
около 12% СИ, поступающих на калибровку, имеют
неприемлемую
погрешность.
При
длительной,
особенно многолетней эксплуатации СИ усиливается
роль
факторов,
накапливаемым
воздействие
изменениям
которых
приводит
параметров
к
как
собственно СИ, так и объектов, его окружающих: в них
происходит
6
перестройка
структуры
материалов,
меняются магнитные свойства, на их поверхность
нарастают осадки и т.д.

7.

Проблема повышения достоверности
Риск поступления недостоверной информации
по названным причинам возрастает, причем, как
правило, он превышает риск метрологического отказа,
трактуемого
как
характеристики
установленные
может
"выход
средства
пределы".
произойти
и
из-за
метрологической
измерений
за
Метрологический
отказ
изменения
параметров
модели
измерений, которые не являются параметрами
7
СИ.

8.

Проблема повышения достоверности
Характерно, что в отличие от обычного отказа
СИ, сопровождаемого резким изменением уровня или
вида сигнала на его выходе, метрологический отказ
СИ может быть не замечен.
В большинстве случаев процедуры поверки и
калибровки
предусматривают
оборудования,
его
демонтаж
транспортировку
к
СИ
из
эталону
и
обратно, а затем монтаж на прежнее место. При
8
поверке
и
калибровке
обычно
не
проверяется,
сохраняются ли в допустимых пределах те свойства
окружающих
СИ
объектов,
учитываться в модели измерений.
которые
должны

9.

Проблема повышения достоверности
При транспортировке и монтаже возможно
возникновение незамеченных дефектов, которые
окажут влияние на погрешность последующих
измерений. Как следствие, затраты на проведение
периодических поверок и калибровок при всей их
значительности, оказываются не эффективными.
Ситуация усугубляется тем, что конкуренция
вынуждает к сокращению количества и длительности
9
таких
процедур, к повышению интенсивности
эксплуатации оборудования.

10.

Проблема повышения достоверности
Потребитель заинтересован в увеличении
межповерочного или межкалибровочного интервала
(МПИ), по крайней мере, до межремонтного интервала
оборудования (нередко – до 10 и более лет).
Потребность в длительных МПИ вызвана также
созданием автоматических аппаратов, например,
космических, которые должны функционировать без
обслуживания в течение многих лет. Методы
10
определения
МПИ, приведенные в рекомендациях, не
могут обеспечить требуемую достоверность
измерительной информации.

11.

Проблема повышения достоверности
Переход к методам бездемонтажной поверки
(там где это возможно технически) снижает затраты,
но
ситуацию
качественно
не
меняет.
Возникает
противоречие. Для уменьшения износа оборудования
и
снижения
риска
метрологическое
брака
и
аварий
обслуживание
регулярное
должно
осуществляться более детально и проводиться чаще, а
для
повышения
эффективности
эксплуатации
11
оборудования
– как можно быстрее и реже. Необходим
другой подход, который мог бы обеспечить повышение
достоверности измерений в АСУ и снижение затрат на
их обслуживание.

12.

Проблема повышения достоверности
Переход к методам бездемонтажной поверки
(там где это возможно технически) снижает затраты,
но
ситуацию
качественно
не
меняет.
Возникает
противоречие. Для уменьшения износа оборудования
и
снижения
риска
метрологическое
брака
и
аварий
обслуживание
регулярное
должно
осуществляться более детально и проводиться чаще, а
для
повышения
эффективности
эксплуатации
12
оборудования
– как можно быстрее и реже. Необходим
другой подход, который мог бы обеспечить повышение
достоверности измерений в АСУ и снижение затрат на
их обслуживание.

13.

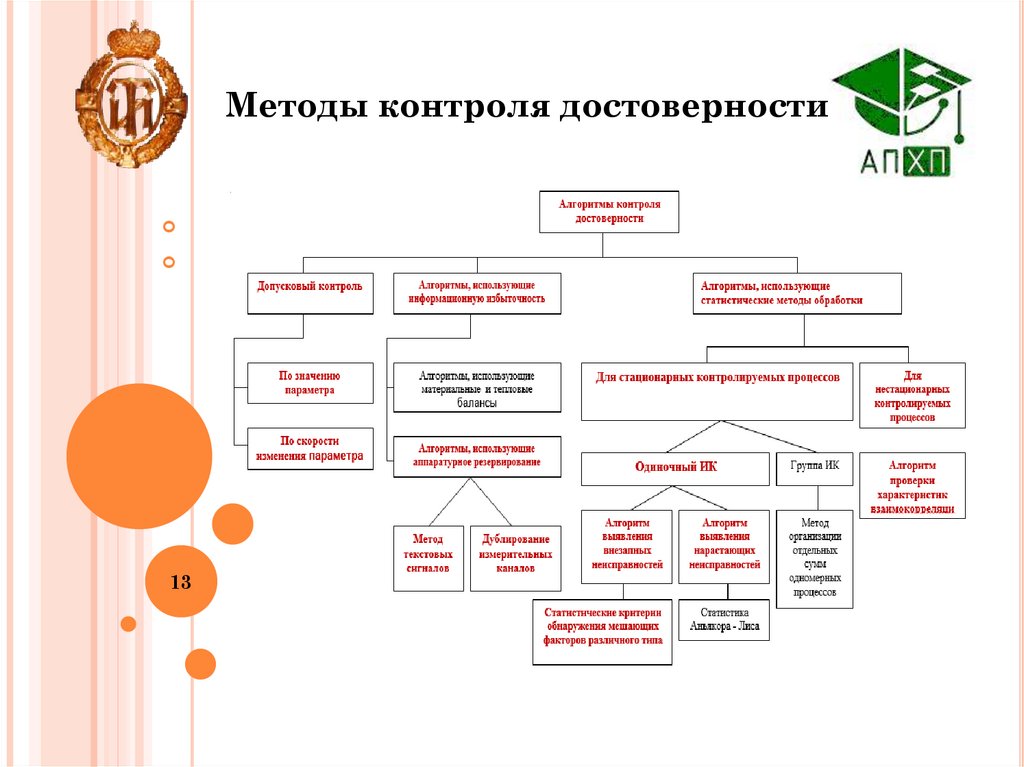
Методы контроля достоверности
13

14.

Методы контроля
достоверности
14
Исходя из того, что входной информацией для систем
управления и диагностики являются измеренные значения
технологических параметров и показания дискретных
датчиков, то эффективность работы систем будет
напрямую
зависеть
от
достоверности
входной
информации.
Поэтому
необходимо
своевременно
выявлять любые нарушения в измерительных каналах.
Как видно из приведенной классификации все
методы (алгоритмы) разбиты на три большие группы:
1). Допусковый контроль;
2). Алгоритмы, использующие информационную
избыточность;
3). Алгоритмы, использующие статистические
методы обработки.

15.

Алгоритмы контроля достоверности
измерительной информации
Понятие достоверности
1 Достоверность - это характеристика знаний как
обоснованных, доказанных, истинных.
2 Достоверность – это свойство информации
отражать реально существующие объекты с необходимой
точностью.
3 Под достоверностью понимается свойство
информации давать сведения характеризующиеся
погрешностями, не выходящими за пределы допустимых
значений.
15
4 Достоверность измерений – это показатель
степени доверия к результатам измерения, то есть
вероятность отклонений измерения от действительных
значений.

16.

Алгоритмы контроля достоверности
измерительной информации
5 Достоверность может быть определена численно,
следуя следующему определению:
Достоверность –
это вероятность отсутствия в измерительной
информации аномальных ошибок различного рода.
D = 1 – Pош.
Здесь Pош – вероятность аномальной ошибки.
К аномальным ошибкам относятся: выбросы,
монотонный дрейф, сдвиги, искажения формы пика.
Точность измерения – это свойство, которое
16 отображает близость результатов измерений к
истинным значениям измеряемых величин.
Точность измерений – степень приближения
измерения к действительному значению величины

17.

Алгоритмы контроля
достоверности
измерительной информации
Для контроля достоверности результатов
измерения используют:
алгоритмы допускового контроля и
алгоритмы статистического контроля.
В алгоритмы допускового контроля
входят:
а) алгоритм отбраковки информации по
диапазону возможных изменений;
17
б) алгоритм отбраковки информации по
диапазонам изменения переменной и по ее
производной.

18.

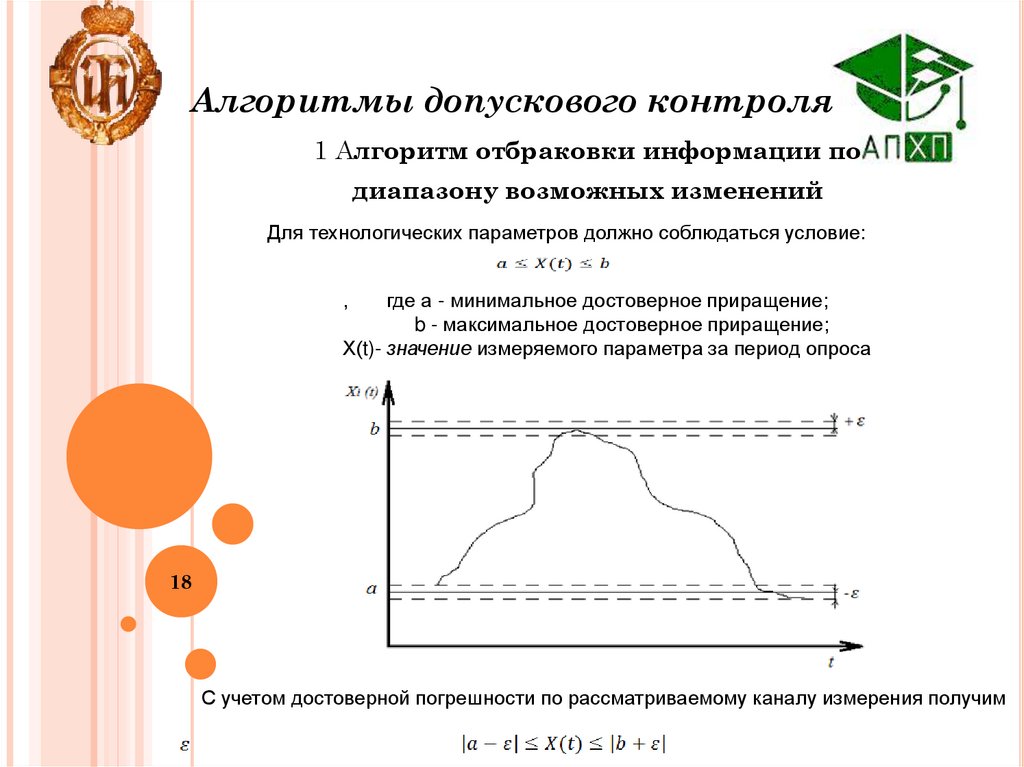
Алгоритмы допускового контроля
1 Алгоритм отбраковки информации по
диапазону возможных изменений
Для технологических параметров должно соблюдаться условие:
,
где а - минимальное достоверное приращение;
b - максимальное достоверное приращение;
Х(t)- значение измеряемого параметра за период опроса
18
С учетом достоверной погрешности по рассматриваемому каналу измерения получим

19.

Алгоритмы допускового
контроля
2 Алгоритм отбраковки информации по
диапазонам изменения переменной и по ее
производной
,
Для технологических параметров должны соблюдаться условия допускового контроля:
где
- скорость изменения измеряемого параметра за период
опроса,
с- минимальное достоверное приращение при двух
последовательных опросах,
d - максимальное достоверное приращение,
t - период опроса
19
Итоговая формула для проверки скорости изменения:
Здесь с- ∆Хмин,
d-∆Хмах
Допусковая проверка может быть организована для всех измеряемых
аналоговых параметров.

20.

Допусковый контроль текущего значения
сигнала датчика и скорости его изменения в виде
блок-схемы
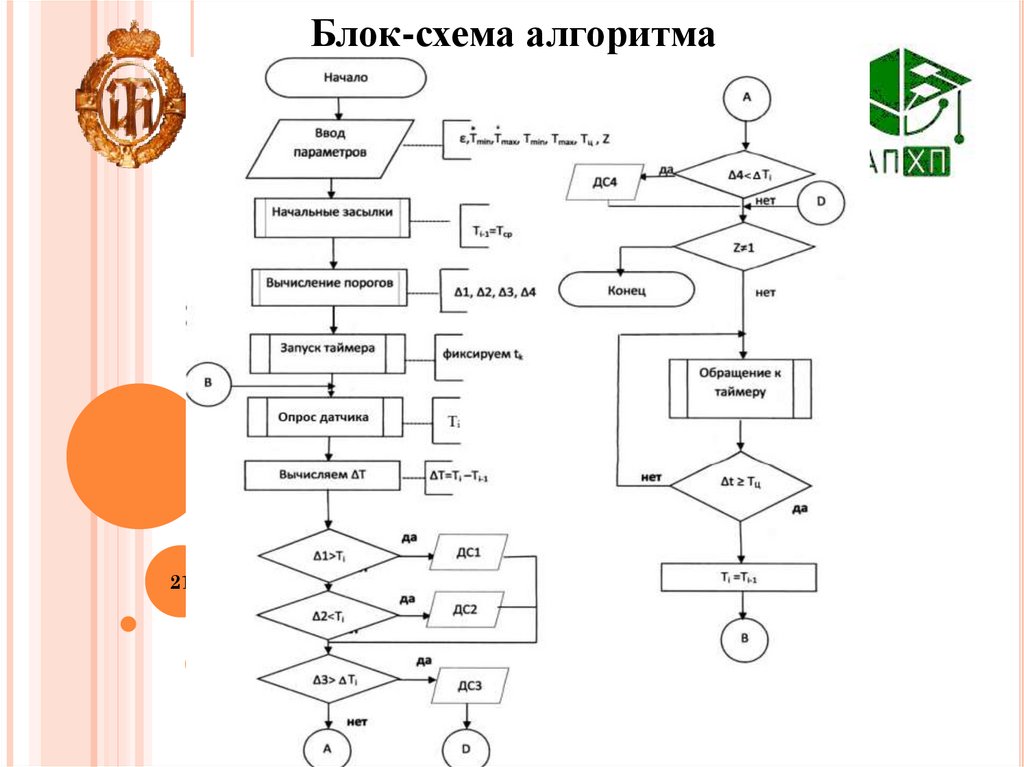
В алгоритме допускового контроля рассчитываются
следующие пороги:
l=Xmin-
2=Xmax+
3= Xmax+2
4= Xmin-2
В качестве измеряемого параметра рассматривается
канал измерения температуры Т.
Результат каждой проверки представляется
диагностическим сообщением оператору
ДС1, ДС2, ДС3, ДС4.
Для работы алгоритма необходимо ввести:
Тmin, Тmax, Тmin , Тmax, , дискретность опроса Тц,
20
признак окончания алгоритма Z/

21.

Блок-схема алгоритма
21

22.

Статистические алгоритмы
контроля достоверности
22
В этих алгоритмах используют разнообразные
критерии
для
обнаружения
каких-либо
аномальностей
в
измеряемом
параметре.
Статистические методы основаны на теории
проверки статистических гипотез.
Общий алгоритм обнаружения аномальных
результатов включает:
1Расчет статистики
Под статистикой понимают любую функцию от
элементов выборки:
2 Критерием проверки гипотезы является
решающее правило, которое позволяет по данной
выборке отвергнуть или принять высказываемую
гипотезу. Решающим правилом является сравнение
рассчитанной статистики с ее критическим
значением. По результатам сравнения
определяется, какая гипотеза правильна. При
принятии гипотезы могут быть сделаны ошибки 1го (верна H1 , а H0 отвергается) или 2-го рода ( H0верна, а H1- неверна).

23.

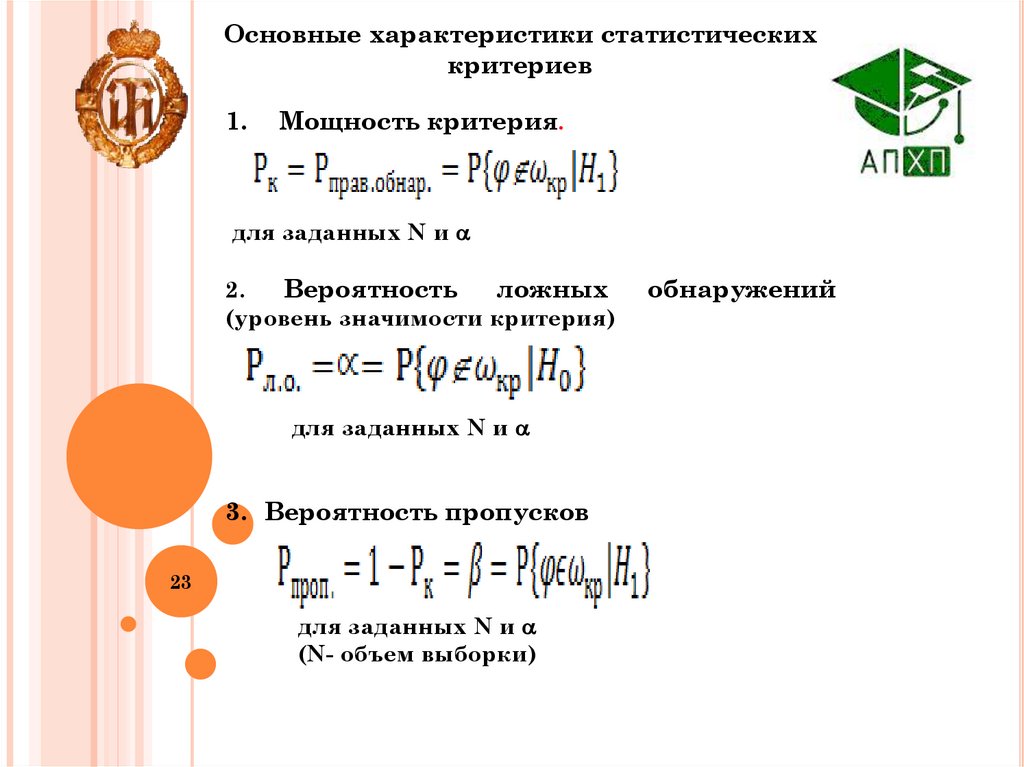
Основные характеристики статистических
критериев
1.
Мощность критерия.
для заданных N и
2.
Вероятность
ложных
(уровень значимости критерия)
для заданных N и
3. Вероятность пропусков
23
для заданных N и
(N- объем выборки)
обнаружений

24.

Статистические алгоритмы контроля
достоверности включают:
-алгоритмы обнаружения выбросов;
-алгоритмы обнаружения монотонного
дрейфа;
-алгоритмы выявления сдвинутых
значений;
24
-алгоритмы обнаружения искажений
формы пика.

25.

Классификация критериев обнаружения
аномальных ошибок
:
По виду используемой тестовой статистики критерии
можно разделить на 4 группы:
-критерии, основанные на статистиках,
характеризующих отклонение одного или
нескольких элементов выборки от основной группы
значений (обычно от оценки математического
ожидания);
-критерии, основанные на статистиках,
характеризующих отклонение одного или
нескольких элементов выборки от соседних членов
вариационного ряда;
25
-критерии, основанные на статистиках,
характеризующих отношение дисперсий;
-критерии, основанные на использовании
нормированных третьего и четвертого центральных
моментов

26.

Критерии обнаружения выбросов
Под аномальной (грубой) ошибкой, выбросом,
выскакивающей вариантой понимают частный
вид случайной ошибки, по значению намного
превосходящей заданные характеристики
измерительной системы
Критериев обнаружения выбросов
десятки в зависимости от постановки
задачи идентификации аномальной
ошибки.
26
Рассмотрим два из них:
-критерий Диксона ,
-критерий Смирнова-Граббса.

27.

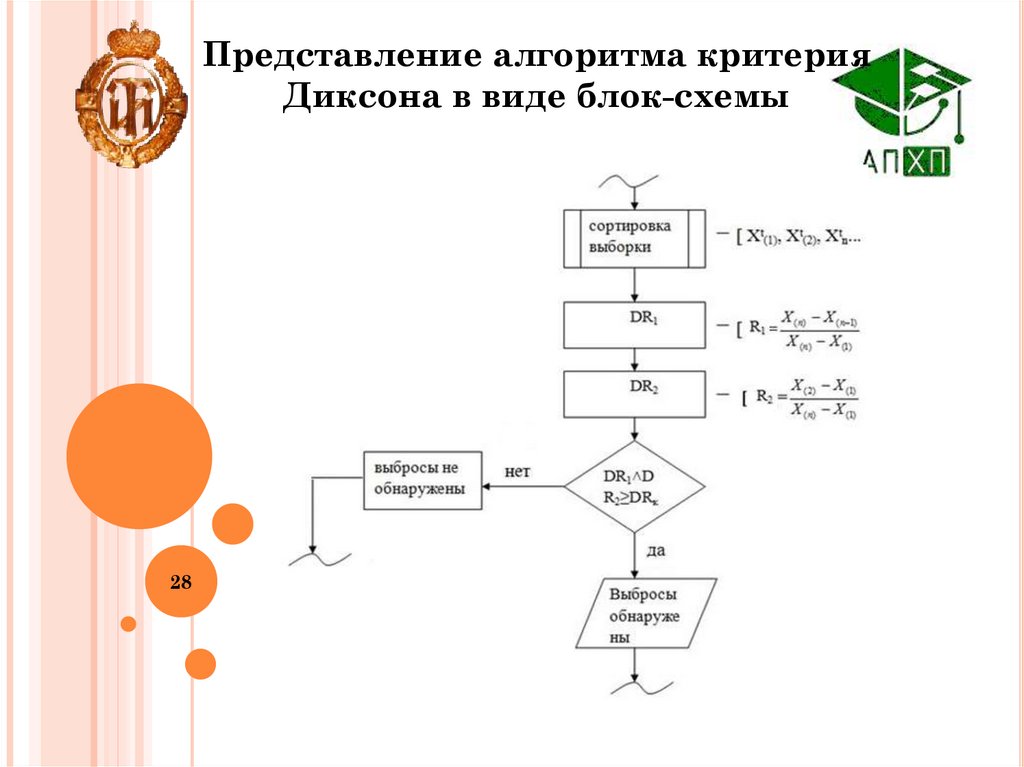
Критерий Диксона:
Статистика для выявления максимального значения
выборки имеет вид:
– максимальное подозреваемое на выброс значение выборки
Статистика для выявления минимального значения
выборки имеет вид:
y(1) - минимальное подозреваемое на выброс значение
выборки;
Решающее правило:
Если
– выброс не обнаружен.
Если
-выброс,
27
-выброс.
Достоинством критерия является простота, но при его
использовании требуется сортировка или ранжирование
элементов.

28.

Представление алгоритма критерия
Диксона в виде блок-схемы
нет
да
28

29.

Представление алгоритма
критерия Диксона в форме ЯЛС
29

30.

Алгоритмы сортировок
Сортировка – это процесс упорядочивания набора данных
одного типа по убыванию или возрастанию какого-либо
признака.
Существуют десятки видов сортировки:
-сортировка элементов массива;
-сортировка строк;
-сортировка элементов файла.
На практике используют чаще всего следующие виды
сортировок элементов массива:
-Сортировка простыми вставками.
-Сортировка простым выбором.
-Простая обменная сортировка или метод пузырька.
30
-Метод быстрой сортировки- метод ХОАРА.
Сортировка простыми вставками подходит для случая,
когда данные поступают последовательно, например в
результате опроса датчика.

31.

Критерий Смирнова-Граббса:
Статистика для выявления максимального значения
выборки имеет вид:
– максимальное подозреваемое на выброс значение выборки
-математическое ожидание, S-СКО
Статистика для выявления минимального значения
выборки имеет вид:
y(1) - минимальное подозреваемое на выброс значение
выборки;
Решающее правило:
Если
– выброс не обнаружен.
31
Если
y(n) -выброс,
y(1) -выброс.
Достоинством критерия является простота, но он обладает
маскирующим эффектом.

32.

.
Критерий Смирнова-Граббса
н
32
.

33.

Критерий для обнаружения
монотонного дрейфакритерий Аббе
.
-значения выборки.
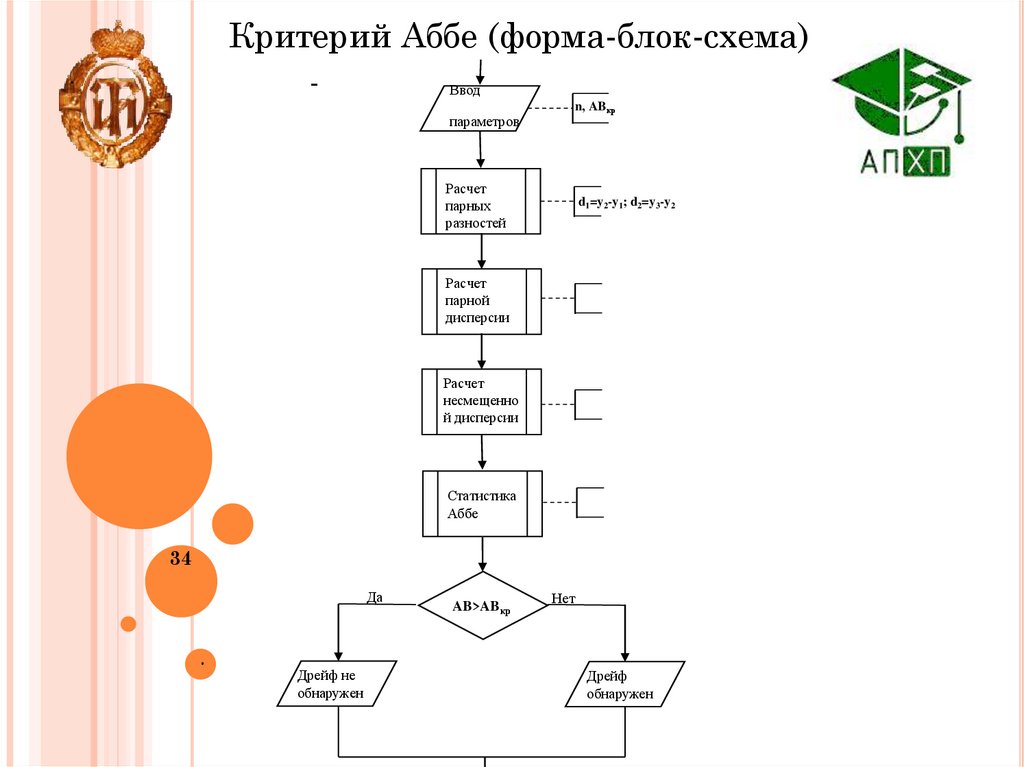
1 Сначала рассчитываются парные разности:
2. Далее идет вычисление парной дисперсии:
3. Вычисляется несмещенная дисперсия:
4. Затем рассчитывается статистика Аббе:
33
5. Решающее правило:
Если,
то выборка однородна и дрейф отсутствует
Если,
то дрейф обнаружен

34.

Критерий Аббе (форма-блок-схема)
-
.
Ввод
n, ABкр
параметров
Расчет
парных
разностей
d1=y2-y1; d2=y3-y2
Расчет
парной
дисперсии
Расчет
несмещенно
й дисперсии
Статистика
Аббе
34
Да
.
Дрейф не
обнаружен
AB>ABкр
Нет
Дрейф
обнаружен

35.

Обнаружение повышенного уровня шума
(форма-ЯЛС)
35

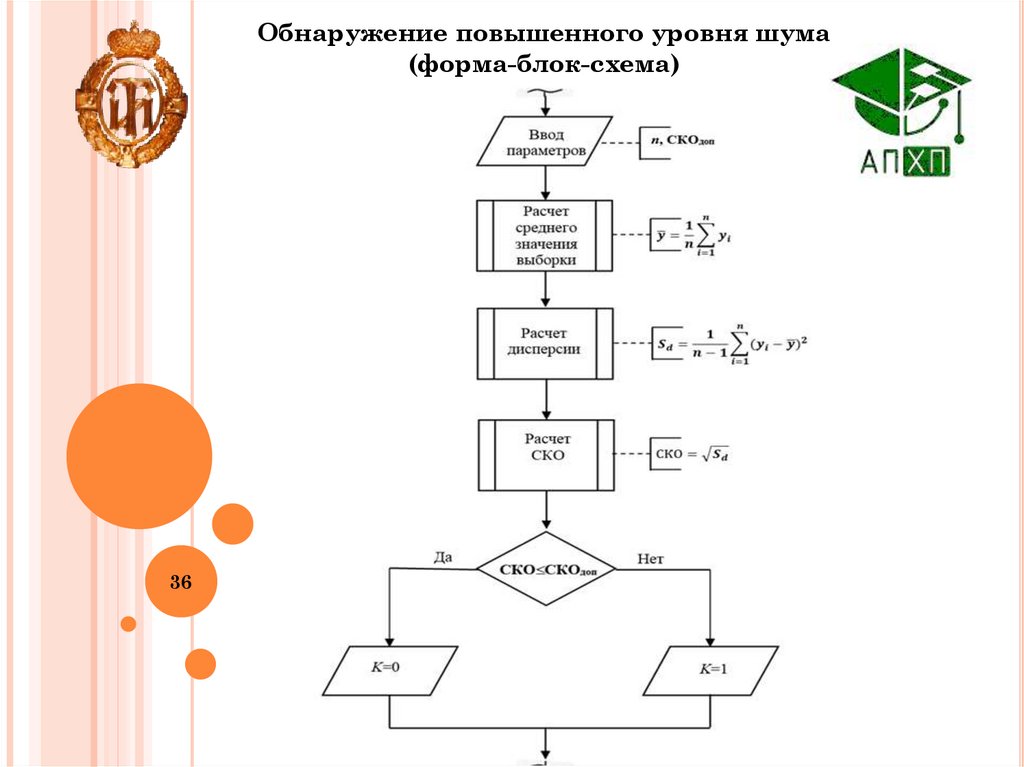
36.

Обнаружение повышенного уровня шума
(форма-блок-схема)
36

37.

Статистические критерии для выявления
сдвинутых значений
Статистические
методы
обнаружения
сдвинутых
наблюдений базируются на проверке допустимого
различия между оценками средних значений двух групп
наблюдений.
Рассмотрим два случая когда:
-выборки не коррелированы;
-выборки коррелированы.
37

38.

Статистические критерии для выявления
сдвинутых значений
38

39.

Статистические критерии для выявления
сдвинутых значений
39

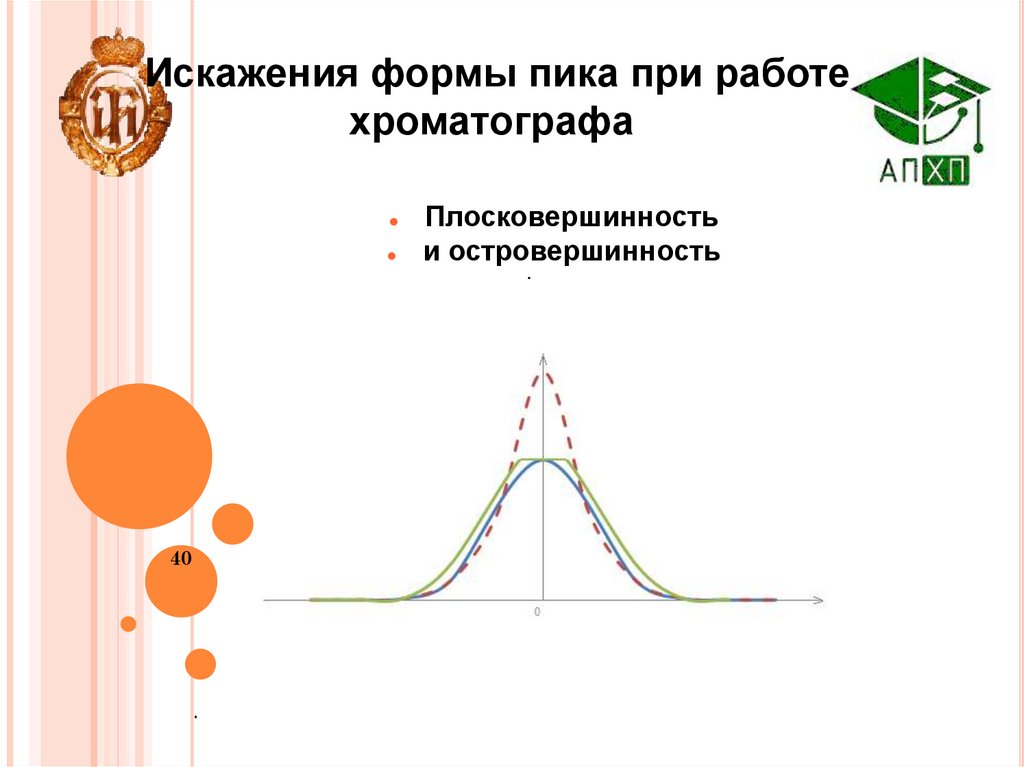
40.

Искажения формы пика при работе
хроматографа
Плосковершинность
и островершинность
.
40
.

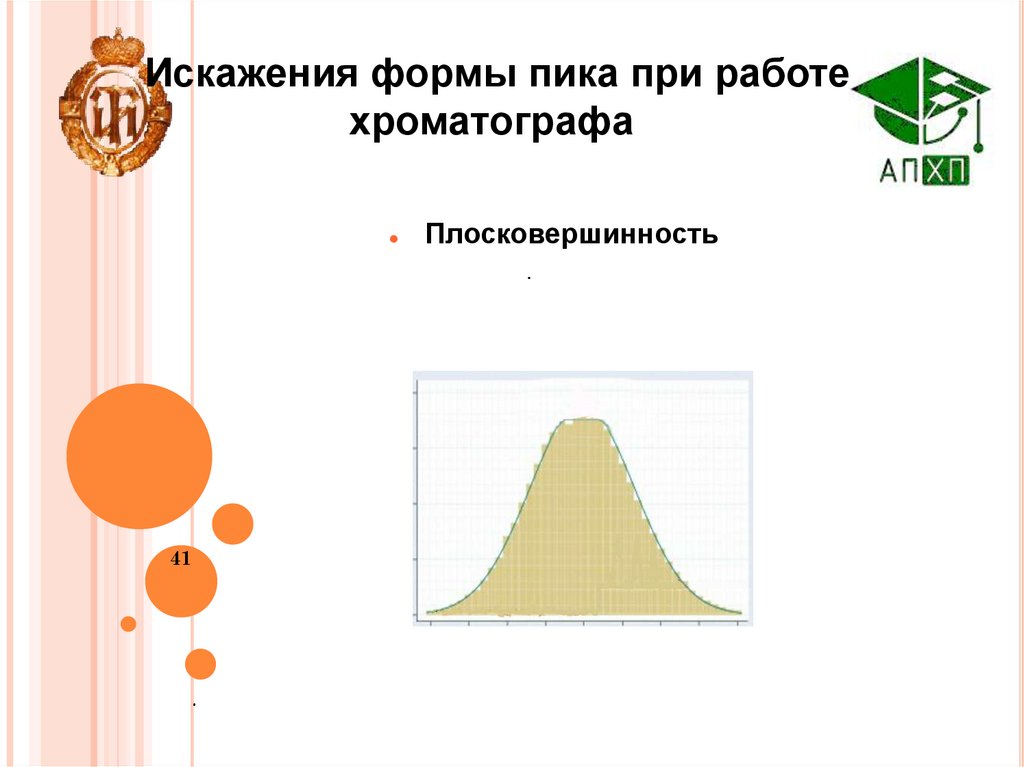
41.

Искажения формы пика при работе
хроматографа
Плосковершинность
.
41
.

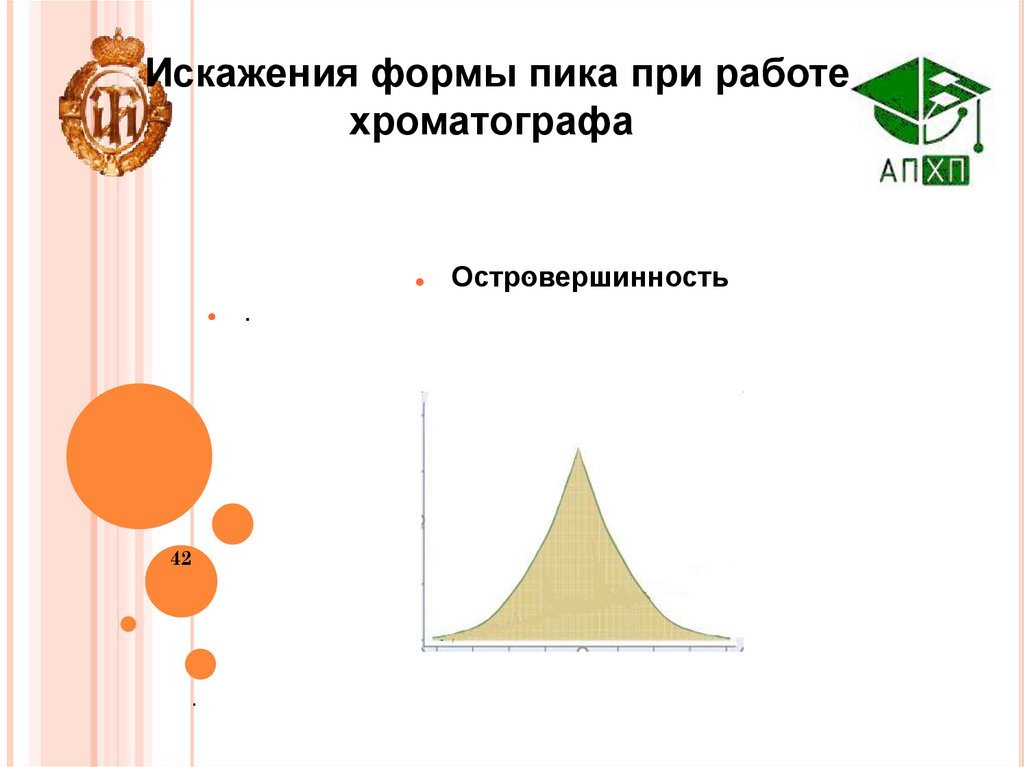
42.

Искажения формы пика при работе
хроматографа
42
.
.
.
Островершинность

43.

Алгоритм обнаружения плоско- и
островершинности
Четвертый центральный момент (показатель эксцесса)
рассчитывается по формуле:
.
где
Задаем порог ∆
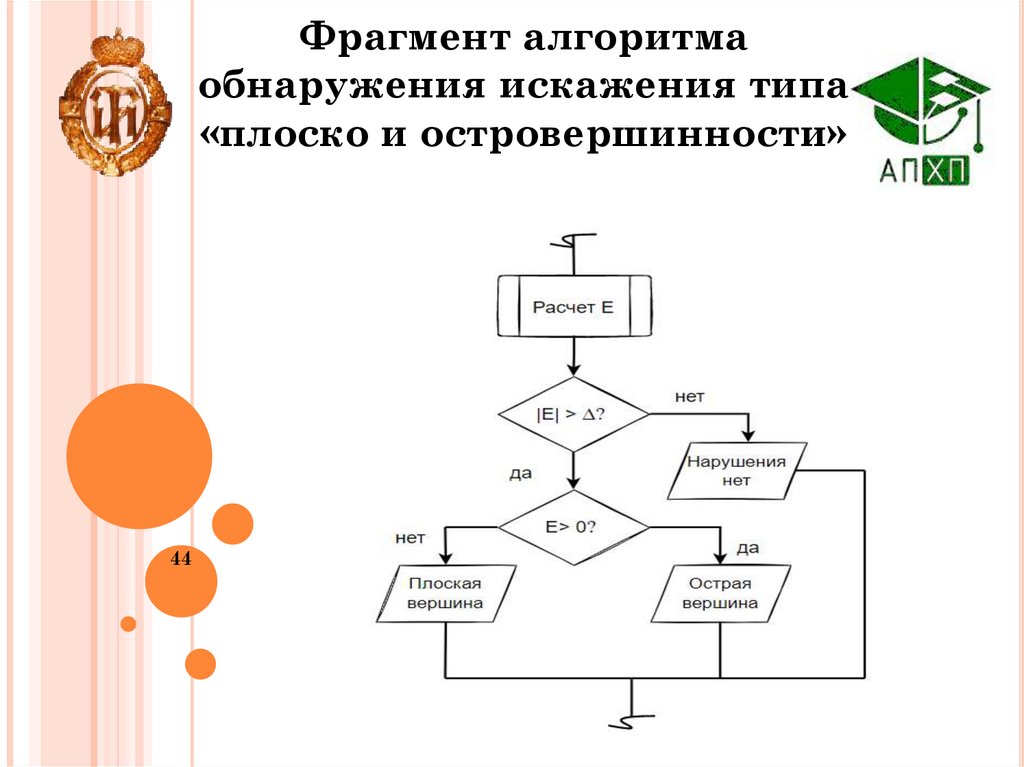
Решающие правила алгоритма:
Если E > ∆ - Обнаружено отклонение.
Если E < 0 - Плоская вершина пика.
.
Если E > 0 – Острая вершина пика.
43

44.

Фрагмент алгоритма
обнаружения искажения типа
«плоско и островершинности»
44

45.

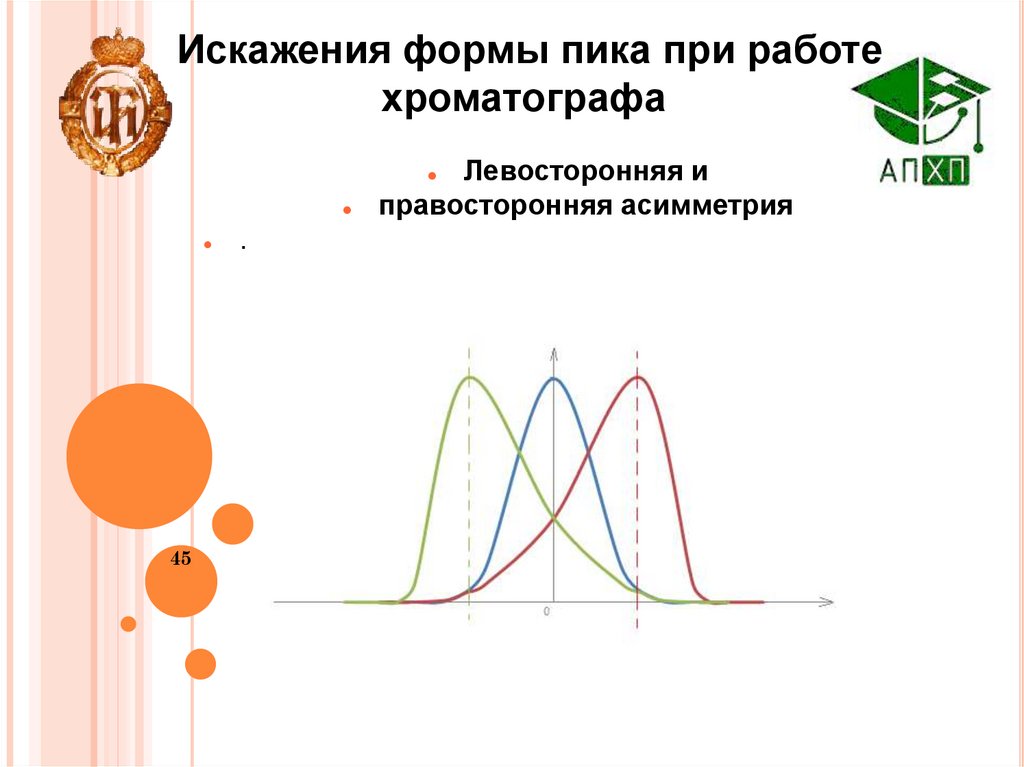
Искажения формы пика при работе
хроматографа
Левосторонняя и
правосторонняя асимметрия
45
.

46.

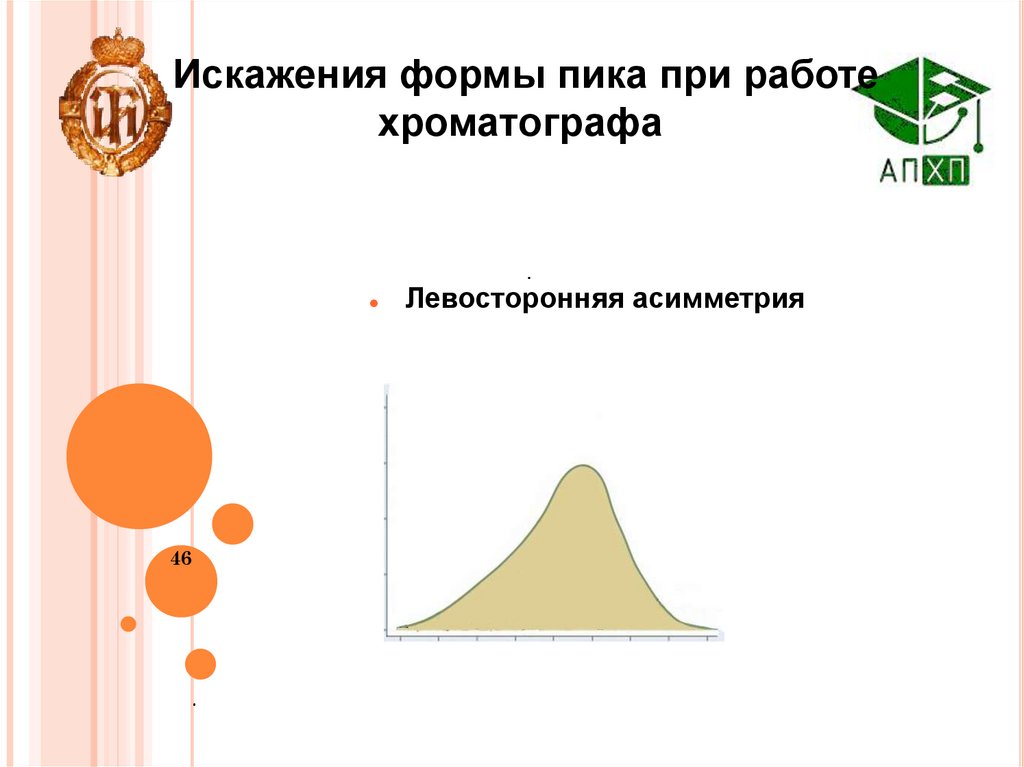
Искажения формы пика при работе
хроматографа
.
46
.
Левосторонняя асимметрия

47.

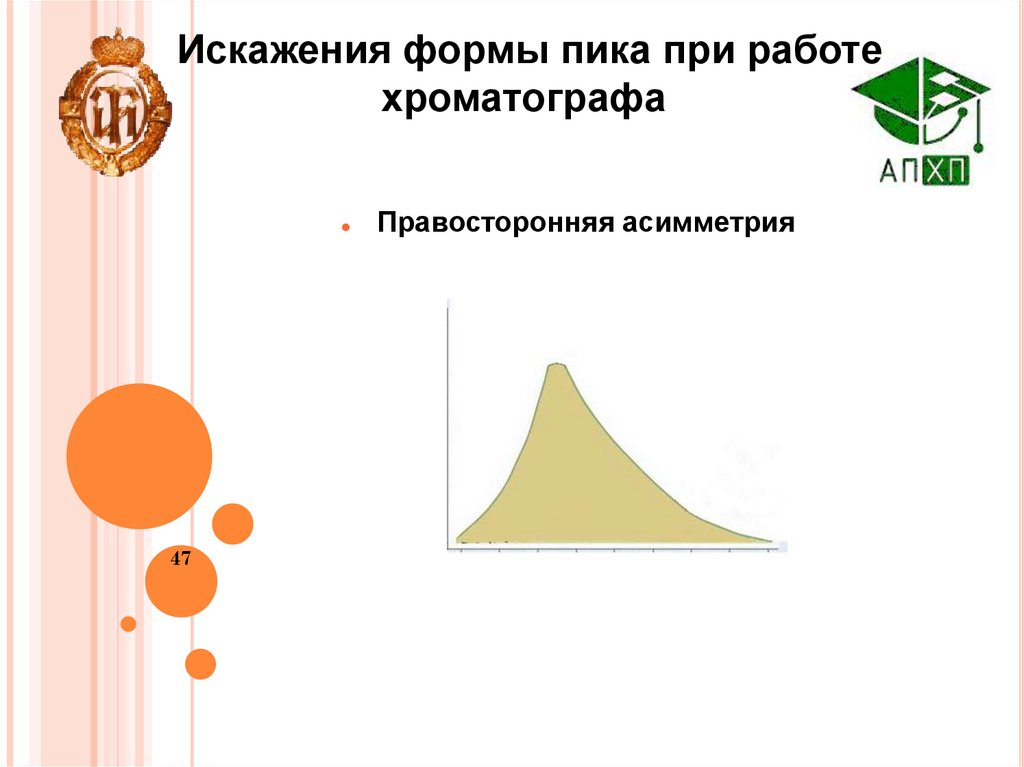
Искажения формы пика при работе
хроматографа
47
Правосторонняя асимметрия

48.

Алгоритм обнаружения
искажения типа «асимметрия»
48
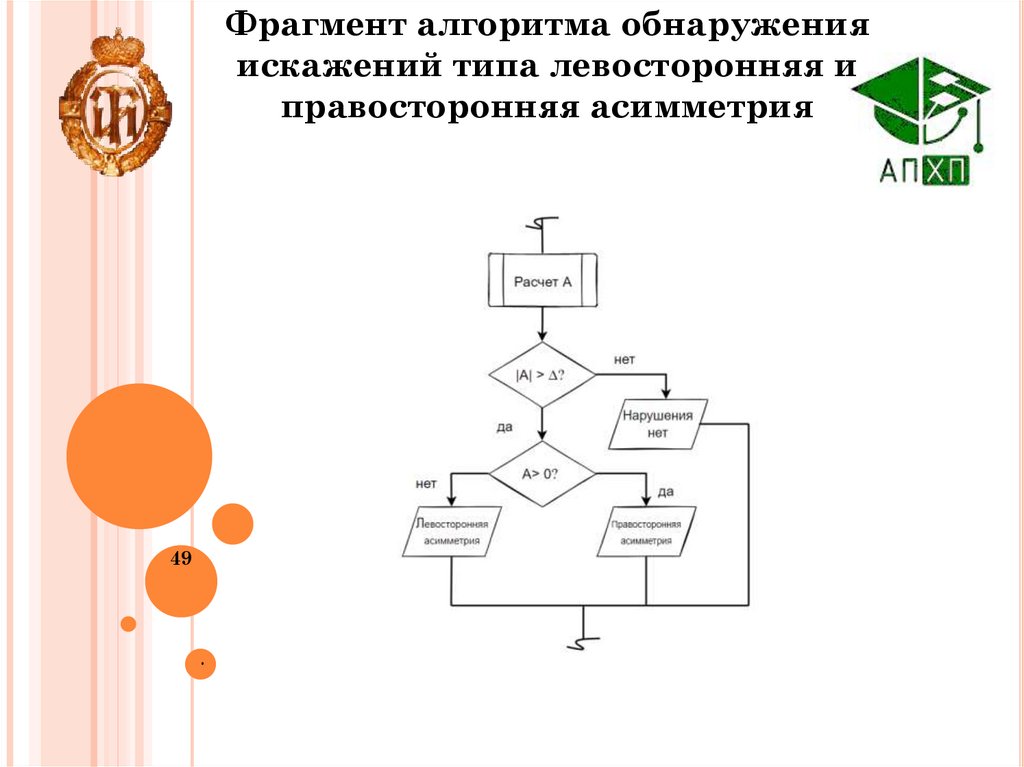
Решающие правила алгоритма:
-выбираем некий порог ∆
если |A| > ∆ - асимметрия обнаружена;
если A < 0 – левосторонняя
асимметрия;
если A > 0 – правосторонняя
асимметрия.

49.

Фрагмент алгоритма обнаружения
искажений типа левосторонняя и
правосторонняя асимметрия
.
49
.

50.

Спасибо за внимание!
.
.
50

51.

Спасибо за внимание
51

52.

Спасибо за внимание
52