lektsia_01

1. Квантовая теория твердого тела

Профессор Светлана Евгеньевна Кулькова kulkova@ispms.ru
Рекомендуемая литература:
1. Ч. Киттель. Введение в физику твердого тела. -М.: Наука, 1978, 270с.
2. Н.Ашкрофт, Н. Мермин. Физика твердого тела.- М.: Мир, 1979, Т.1,2.
3. Дж. Блекмор. Физика твердого тела. .- М.: Мир, 1988
4. Дж. Займан. Принципы физики твердого тела. .- М.: Мир, 1974.
5. Дж. Каллуэй. Теория энергетической зонной структуры.- М.: Мир,
1969.
6. Г.Джонс. Теория зон Бриллюэна и электронные состояния в
кристалле. - М.: Мир, 1968.
7. Дж. Слэтер. Методы самосогласованного поля для молекул и твердых
тел. -М.: Мир, 1978
8. В.В. Немошкаленко и В.И. Антонов. Методы вычислительной физики
в теории твердого тела, зонная теория металлов. –Киев: Наукова Думка,
1985, 407с.

2. ЦЕЛЬ КУРСА

Дать целостное представление о процессах и явлениях, происходящих в
твердом теле и возможностях современных научных методов познания
твердого тела на микроскопическом и макроскопическом уровнях.
Дать представление об электронной структуре, зонной теории и
электрических процессах в твердом теле.
Рассмотреть фундаментальные свойства металлов и полупроводников, а
также заложить базисные представления для понимания процессов и
явлений в твердом теле.

3.

4.

5.

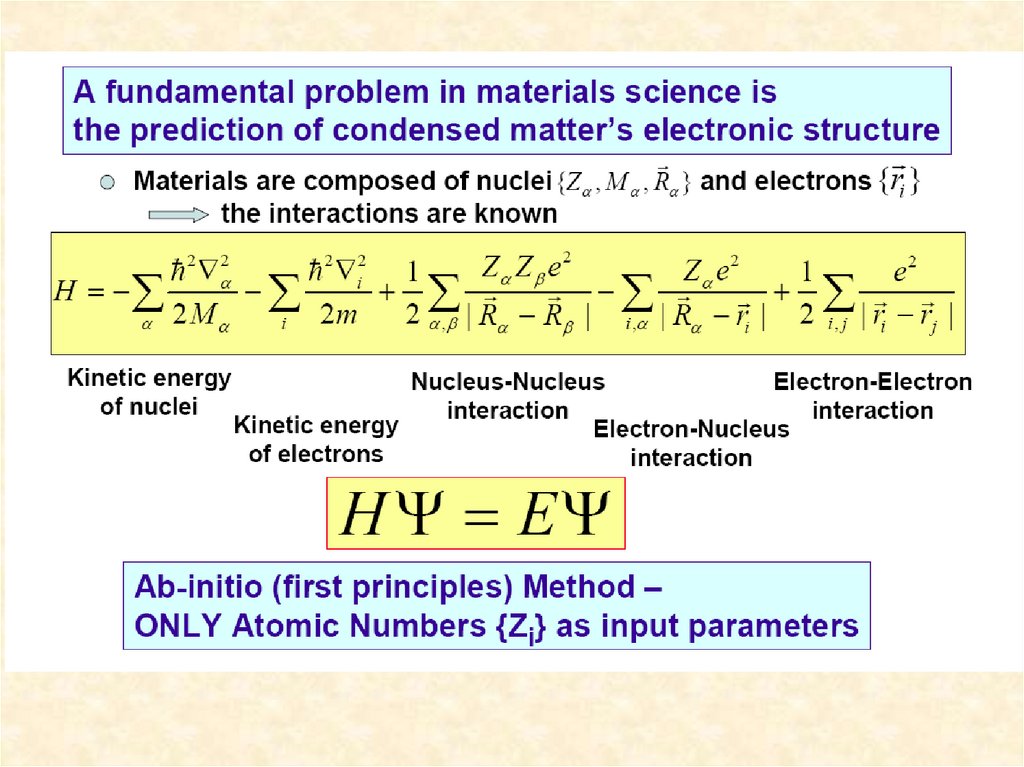
Тема 1: Электроны в кристаллах
Введение
HΨ=EΨ
Рассмотрим схематично задачу о нахождение
электронных состояний и волновых функций
электрона в кристалле на примере одномерной
системы
а
а
Для одномерной цепочки трансляции совмещающие
решетку с собой имеют вид Т=nа, где n-целое число
изменяющиеся от 0 до N-1, где N – число атомов.

6.

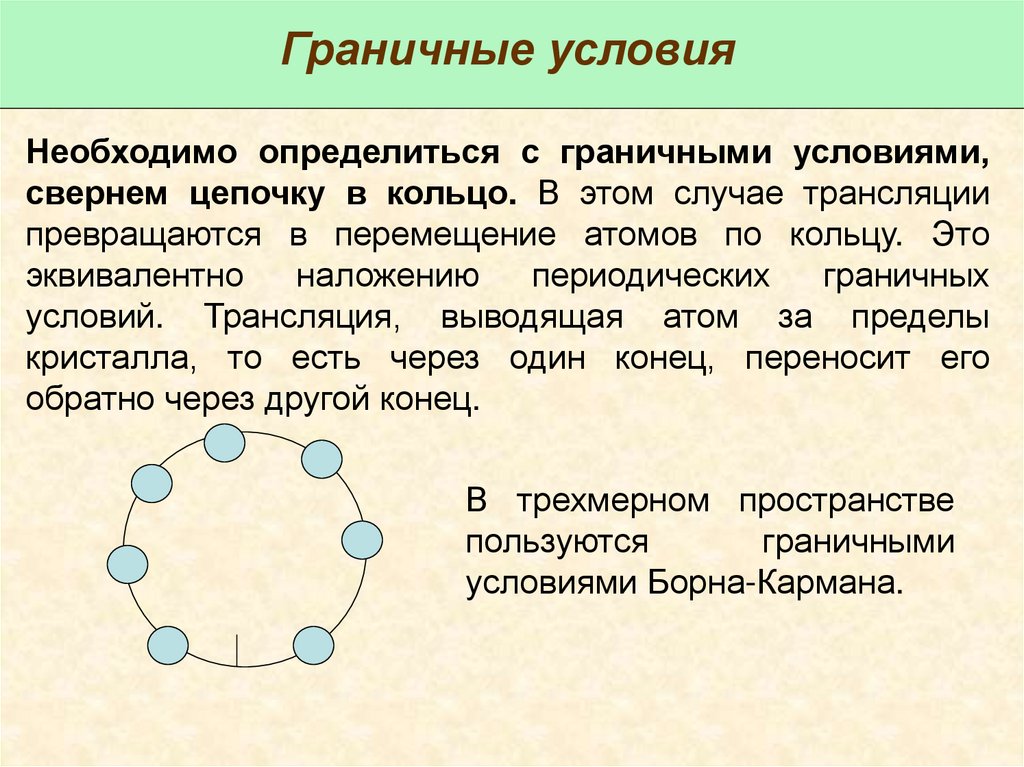
Граничные условия
Необходимо определиться с граничными условиями,
свернем цепочку в кольцо. В этом случае трансляции
превращаются в перемещение атомов по кольцу. Это
эквивалентно
наложению
периодических
граничных
условий. Трансляция, выводящая атом за пределы
кристалла, то есть через один конец, переносит его
обратно через другой конец.
В трехмерном пространстве
пользуются
граничными
условиями Борна-Кармана.

7. Разрешенные k-значения

Периодические граничные условия для трехмерного кристалла
k (x L, y, z) k (x, y, z)
k (x, y L, z) k (x, y, z) k (x, y, z L) k (x, y, z)
k ( r ) A exp( i k r ,) где A –нормировочный множитель. Граничные
условия разрешают существование только определенных дискретных
значений k, таких что eikxL= eikyL= eikzL=1
kx=
2p
2p
2p
;
=
;
=
nx k y
ny k z
nz
L
L
L
Так как
Нормируя
где nx, ny, и nz = +/- 1,2,3…
ψk(x+L) = Aexp[i(kxx+2pnx) ] = Aexp[i(kxx)] = ψk(x)
*
2
2
(
r
)
(
r
)dV
A
exp(
i
k
.
r
)
exp(
i
k
.
r
)
dV
A
V 1
k k
Где объем кристалла V = L3
ψk(r) = V-1/2 exp[ik.r]
Для ky = 0 и kz = 0 разрешенные k-значения однородно распределены
вдоль оси kx в k-пространстве, Эти значения представляют собой
кратные от 2p/L.

8.

Определенные таким образом N трансляций
для
одномерной цепочки образуют группу. Произведение
трансляций
определяется
как
последовательное
выполнение
соответствующих
преобразований.
Единичным элементом является трансляция с n=0. Все
элементы группы коммутируют друг с другом и
представления группы – одномерные. Поскольку каждый
элемент можно представить как степень элемента с n=1,
то группа является циклической, а все неприводимые
представления равны
D(κ)(Tn)=e-2πiκn/N
где κ-целое число, нумерующее представления. N
значений
κ
определяет
все
неприводимые
представления. Обычно κ изменяется от –N/2 до N/2.
–N/2 ≤ κ ≤ N/2, если N –нечетное число, и
–N/2 ≤ κ < N/2, если N –четное число.

9.

10.

11.

12.

13.

14.

15.

Электронные состояния одномерной системы выбираются
так, чтобы каждое из них преобразуется по одному из
неприводимых представлений группы
Введем волновое число k= 2πκ/(Na). Обозначим
собственное состояние, преобразующееся по kпредставлению через Ψk
Это состояние преобразуется под действием операции
симметрии Т следующим образом
TΨk=e-ikT Ψk
Определим новую функцию Uk=e-ikx Ψk, где x – расстояние
вдоль цепочки. Тогда ТUk = Uk, функция Uk инвариантна
относительно всех преобразований трансляции решетки и
электронные состояния представляются в виде
Ψk=Ukeikx - эту запись называют представлением в форме
Блоха. Uk – блоховская функция.

16.

Если бы Uk была бы константой, то собственные состояния
гамильтониана для одномерной цепочки были бы плоскими волнами
свободных
электронов.
Эти
плоские
волны
удовлетворяют
периодическим граничным условиям.
Если Uk не постоянны, то нам удалось установить взаимно
однозначное соотношение между состояниями свободного электрона и
состояниями электрона в кристалле.
Таким образом, методы, используемые для газа свободных
электронов, могут быть приспособлены для исследования состояний в
кристалле.
Значения волнового вектора k ограничены интервалом
-π/a - π/a. Можно всегда любое значение k привести к виду, что
значения будут лежать в этом интервале. Такие значения k-называют
приведенными.
Неэквивалентные значения k ограничены объемом
первой зоны Бриллюэна

17.

18.

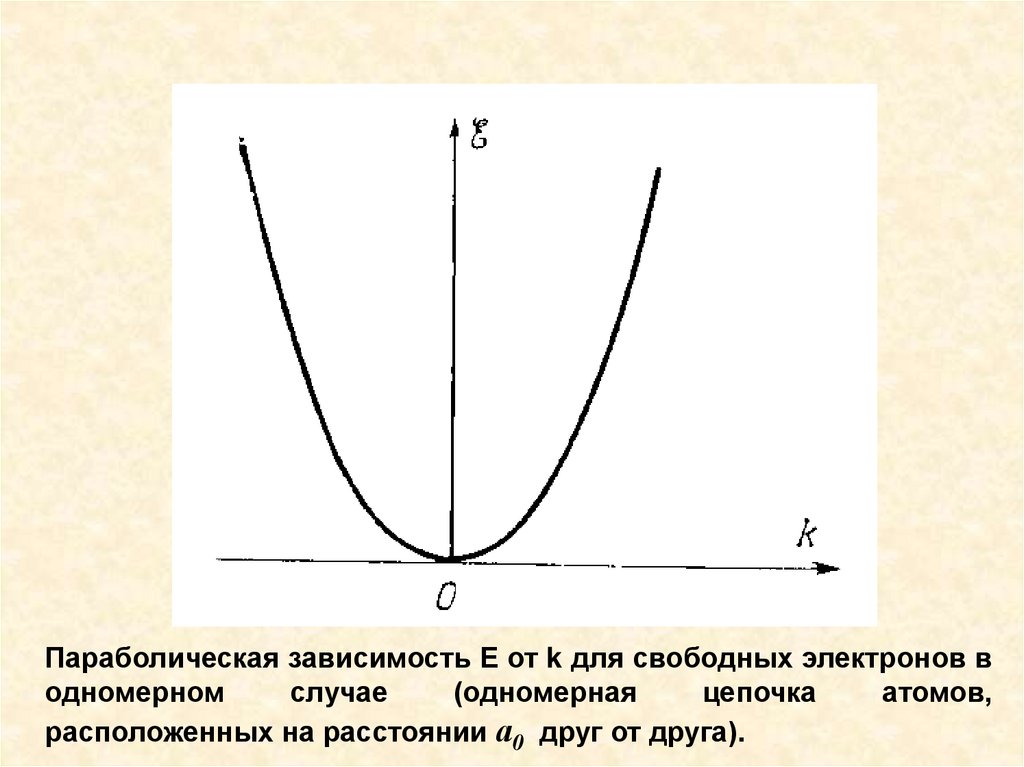
Параболическая зависимость Е от k для свободных электронов в
одномерном
случае
(одномерная
цепочка
атомов,
расположенных на расстоянии а0 друг от друга).

19.

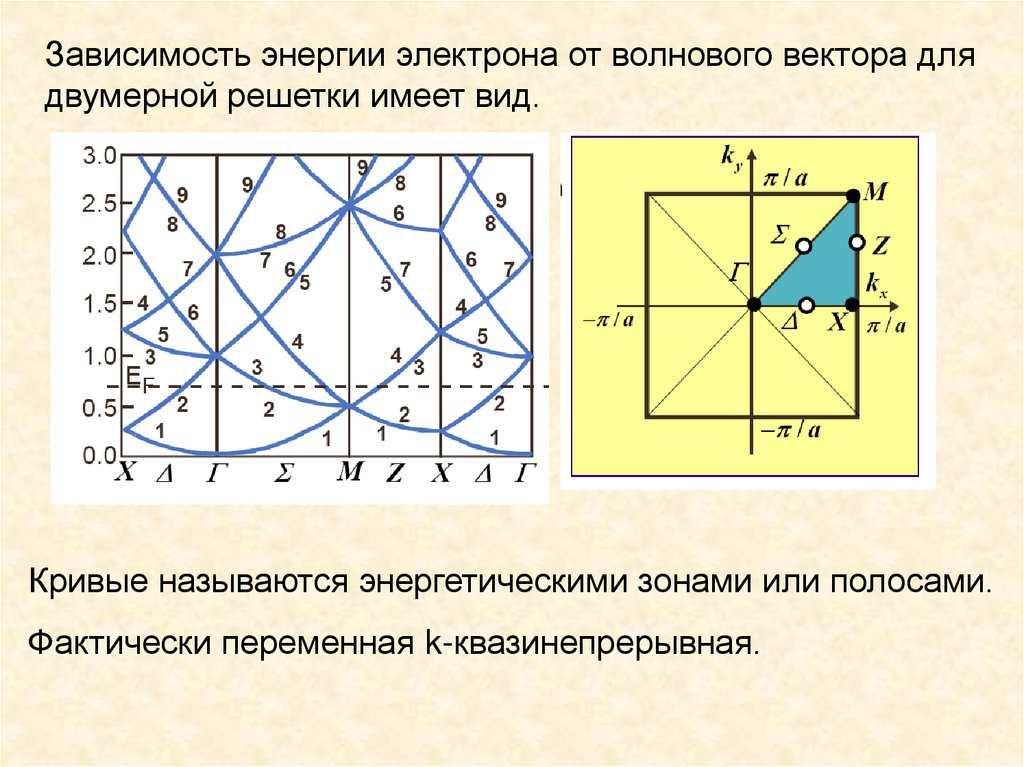
Зависимость энергии электрона от волнового вектора для
двумерной решетки имеет вид.
Кривые называются энергетическими зонами или полосами.
Фактически переменная k-квазинепрерывная.

20.

Пример