17e7737141f94df283738699872adfb6

1.

2.

Билет 1
1. Сформулируйте определение выпуклого многоугольника
(периметр, диагональ). Сформулируйте теорему о сумме
углов выпуклого многоугольника. Четырехугольник.
2. Точки M и N являются серединами сторон AB и BC
треугольника ABC соответственно. Отрезки AN и CM
пересекаются в точке O, AN=24, CM=15. Найдите AO.
3. В окружность вписан треугольник ABC так, что АВ диаметр окружности. Найдите углы треугольника, если
дуга ВС=134°.
4. В равнобедренной трапеции основания равны 4 и 8, а
один из углов между боковой стороной и основанием
равен 45°. Найдите площадь трапеции.

3.

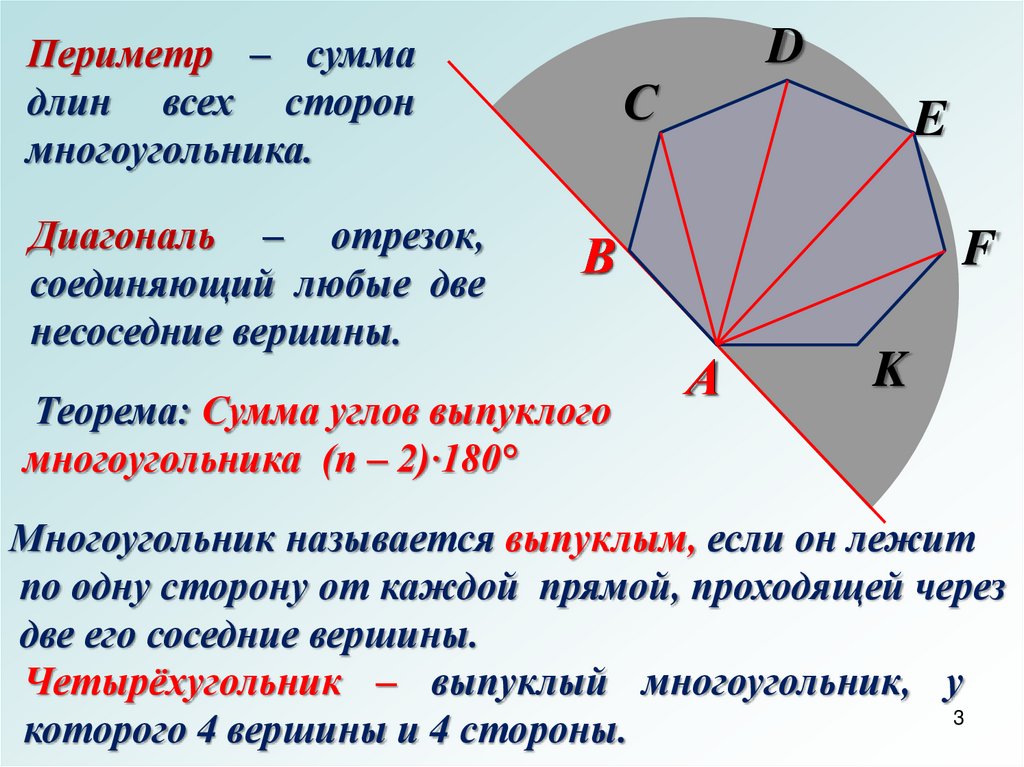
Периметр – сумма
длин всех сторон
многоугольника.
Диагональ – отрезок,
соединяющий любые две
несоседние вершины.
D
С
E
В
Теорема: Сумма углов выпуклого
многоугольника (п – 2)·180°
F
А
K
Многоугольник называется выпуклым, если он лежит
по одну сторону от каждой прямой, проходящей через
две его соседние вершины.
Четырёхугольник – выпуклый многоугольник, у
3
которого 4 вершины и 4 стороны.

4.

Билет № 9.
1. Подобные треугольники. Определение. Коэффициент подобия. Отношение
периметров и площадей подобных треугольников.
2. Окружность с центром в точке O описана около равнобедренного
треугольника ABC, в котором AB = BC и угол ABC = 32°.
Найдите величину угла. BOC. Ответ дайте в градусах.
3. Найдите площадь прямоугольной трапеции АВСD, у которой
основания АВ и CD равны 12 и 20, а больший угол равен 135°.
3
4. В треугольнике АВС ∠С = 90°, cos В = 5, АВ = 45. Найдите АС.

5.

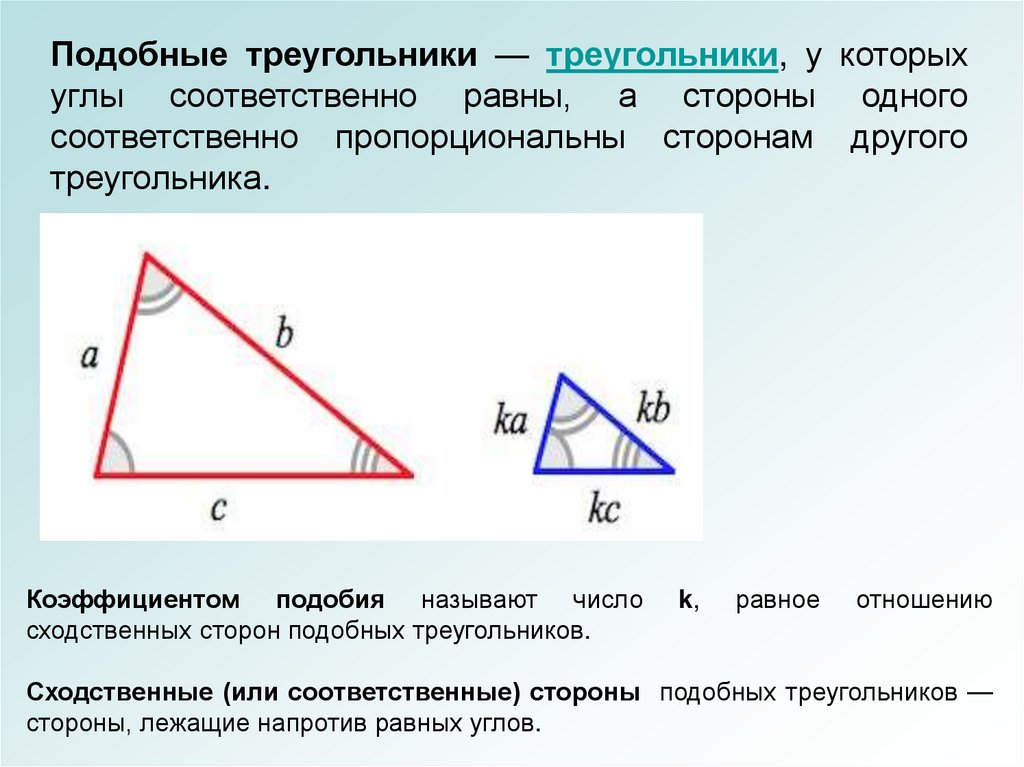
Подобные треугольники — треугольники, у которых
углы соответственно равны, а стороны одного
соответственно пропорциональны сторонам другого
треугольника.
Коэффициентом подобия называют число
сходственных сторон подобных треугольников.
k,
равное
отношению
Сходственные (или соответственные) стороны подобных треугольников —
стороны, лежащие напротив равных углов.

6.

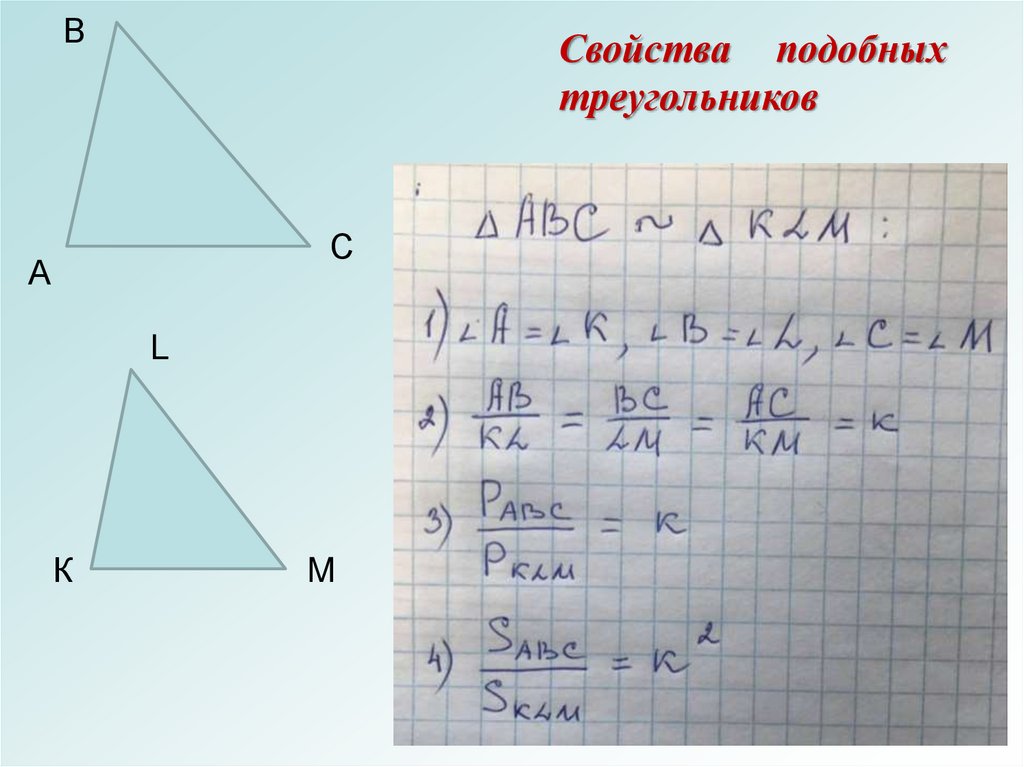
В
Свойства подобных
треугольников
С
А
L
К
M

7.

8.

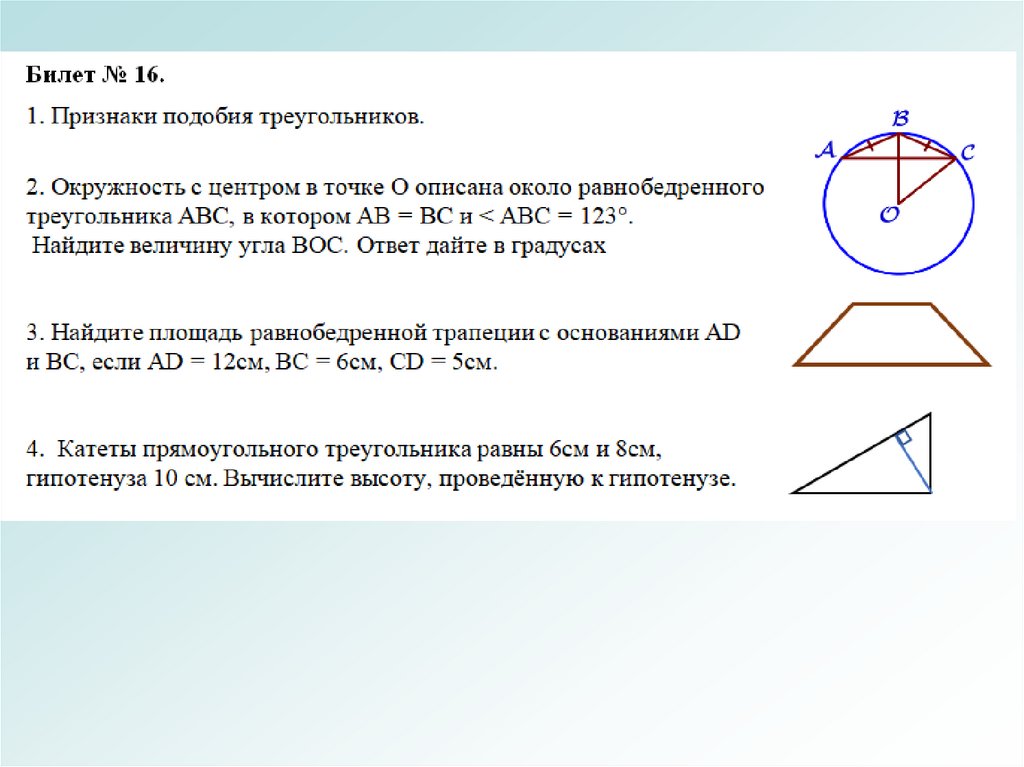
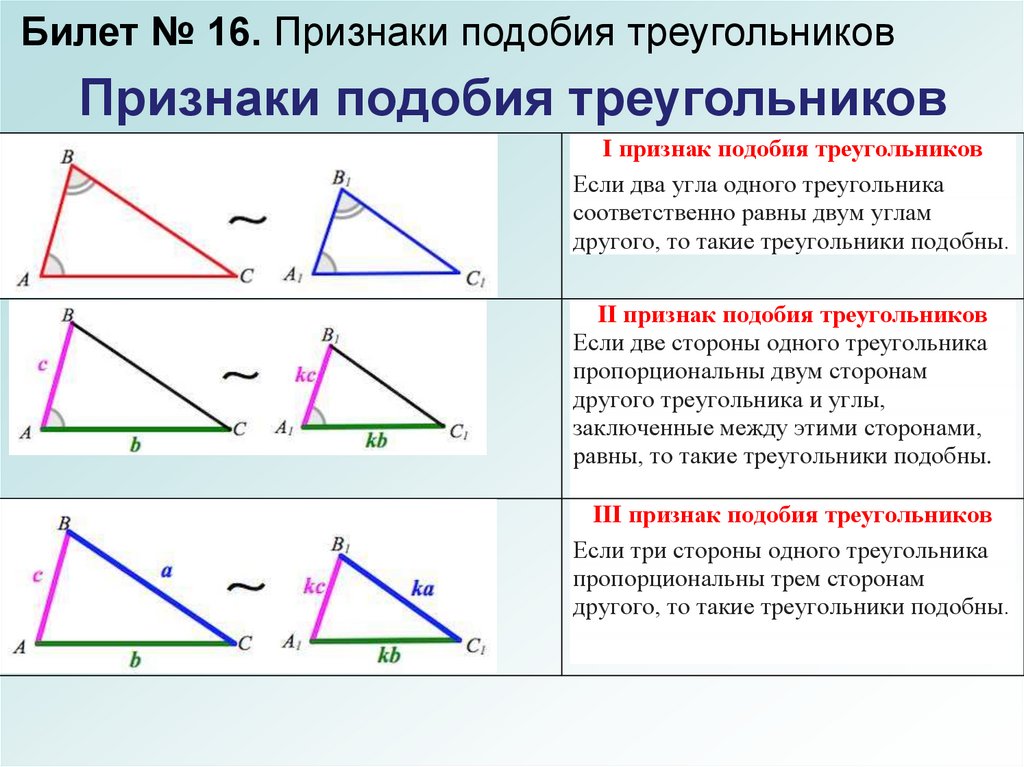
Билет № 16. Признаки подобия треугольников
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника
соответственно равны двум углам
другого, то такие треугольники подобны.
II признак подобия треугольников
Если две стороны одного треугольника
пропорциональны двум сторонам
другого треугольника и углы,
заключенные между этими сторонами,
равны, то такие треугольники подобны.
III признак подобия треугольников
Если три стороны одного треугольника
пропорциональны трем сторонам
другого, то такие треугольники подобны.