Похожие презентации:
Презентация _Своя игра_ по математике для 9 класса
1. МБОУ «СОШ им. А.М. Горького»
Для учащихся 9 класса2. Как пользоваться презентацией
• Чтобы начать игру, переходим к слайду №8, гденаходится меню с выбором вопроса.
• Чтобы перейти непосредственно к выбранному
вопросу, необходимо нажать на стоимость вопроса
данной рубрики. Например, прогрессия за 200.
• Чтобы узнать правильный ответ, нужно нажать на
кнопку «ответ».
• Чтобы вернуться на слайд с рубриками вопросов,
необходимо нажать на стрелку в правом нижнем
углу.
• Обратите внимание, что те вопросы, которые уже
задавались, изменят цвет своей стоимости.
• При завершении работы с презентацией, нажимаем
правую кнопку мыши
и выбираем «Завершить
показ слайдов».
3. Цель и задачи
Цель: проверить уровень подготовкиучеников к сдаче ОГЭ по математике
Задачи:
• повторить материал по темам
«Алгебраические выражения»,
«Графики функций», «Прогрессия»;
• повторить решение геометрических
задачи, уравнений и неравенств ;
• учиться работать в команде.
4. Правила игры
1. Игра проводится между командами. Вкаждой команде по 5-7 человек.
2. Участникам предлагается 5 тем на
выбор. Каждая тема состоит из 5
вопросов разной степени сложности от 100 до 500 баллов. 100 баллов
«стоит» самый простой вопрос темы,
500 — самый трудный.
3. Команды отвечают на вопросы в
порядке очереди.
5. Правила подсчета очков
1. Если команда верно отвечает на данныйвопрос, то она зарабатывает столько
очков,
сколько
«стоит»
заданный
вопрос.
2. Если команда дает неверный или
неточный ответ, то стоимость вопроса
вычитается из ее общего счёта.
3. Команда не обязана отвечать на вопрос,
при этом ее счет не меняется.
4. Когда все вопросы отыграны, суммируют
баллы, полученные командой за игру, и
определяют победителя.
6.
7.
проверить уровень подготовкиучащихся к сдаче ОГЭ по
математике
• повторить материал по темам
«Алгебраические выражения»,
«Графики функций»,
«Прогрессия»;
повторить решение
геометрических задачи,
уравнений и неравенств ;
научиться работать в команде.
8.
9.
Вычислите-1
-3
-4
5 ∙ 10 + 2 ∙ 10 + 1 ∙ 10
Ответ
10.
Вычислите значение выражения5 ∙ 10-1 + 2 ∙ 10-3 + 1 ∙ 10-4
Ответ
0,5021
11.
Найдите значение выраженияb
b
при
a
=
0,2
и
b
=
1,5
2
2
2
a ab a b
Ответ
12.
Найдите значение выраженияb
b
2
2
2 при a = 0,2 и b = 1,5
a ab a b
Ответ
8,5
13.
Найдите значение выражения12ab 2( 3a b) при a = 3 и b = 5
2
Ответ
14.
Найдите значение выражения12ab 2( 3a b) при a = 3 и b = 5
2
Ответ
-64
15.
Найдите значение выражения9
(2 x) x
15
8
x 5x
2
Ответ
16.
Найдите значение выражения9
(2 x) x
15
8
x 5x
2
Ответ
0,8
17.
Найдите значение выражения31a -4b+55, если a - 4b +7
=8
4a -b +7
Ответ
18.
Найдите значение выражения31a -4b+55, если a - 4b +7 = 8
4a -b +7
Ответ
6
19.
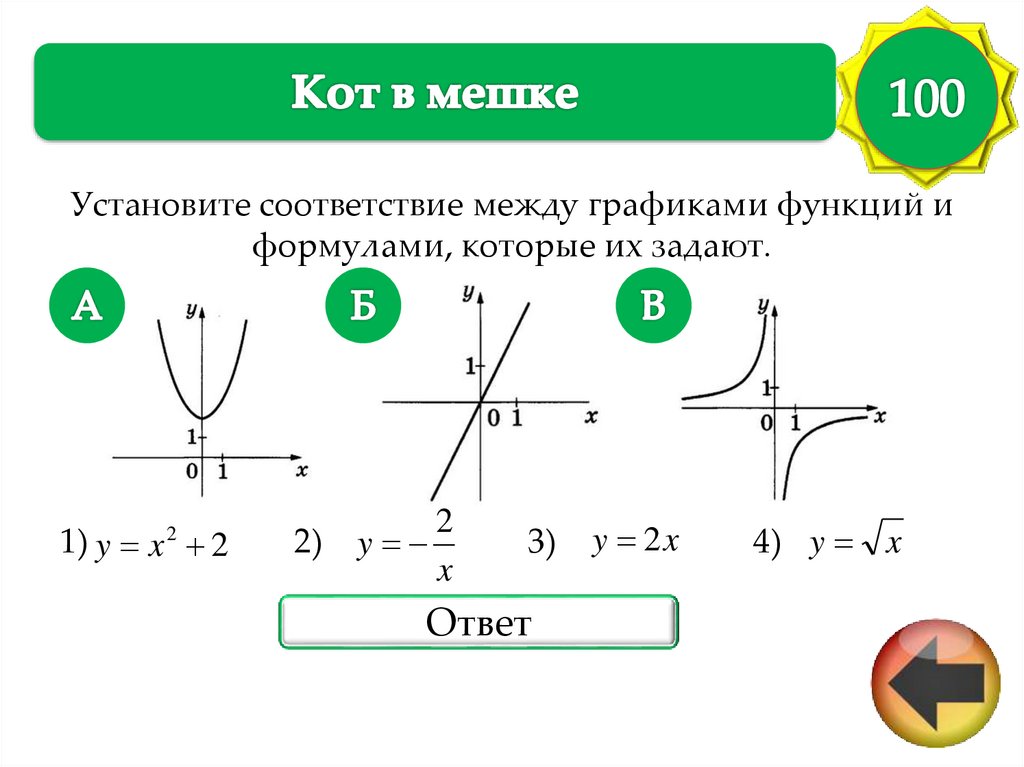
Установите соответствие между графиками функций иформулами, которые их задают.
1) y x 2
2
2)
2
y
x
3)
Ответ
y 2x
4) y x
20.
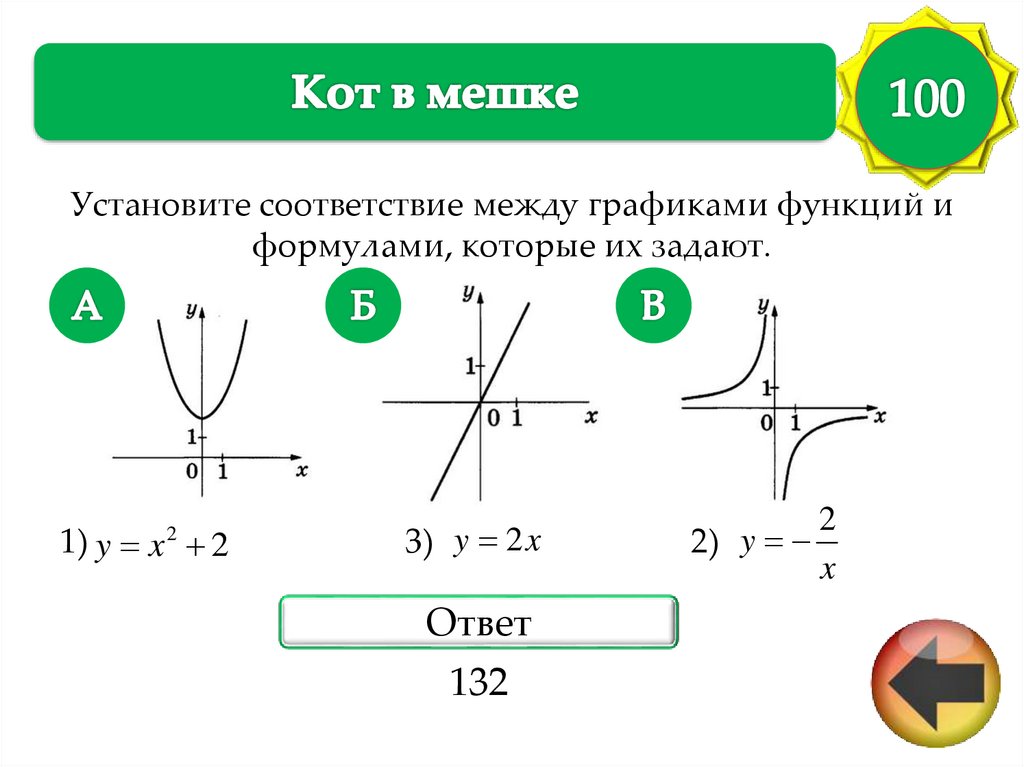
Установите соответствие между графиками функций иформулами, которые их задают.
1) y x 2
2
3) y 2 x
Ответ
132
2) y
2
x
21.
Чтобы перевести значение температурыпо шкале Цельсия в шкалу Фаренгейта,
пользуются формулой F = 1,8 С+32, где С –
градусы Цельсия, F – градусы Фаренгейта.
Какая температура по шкале Фаренгейта
соответствует -43 градусам по шкале
Цельсия?
Ответ
22.
Чтобы перевести значение температурыпо шкале Цельсия в шкалу Фаренгейта,
пользуются формулой F = 1,8 С+32, где С–
градусы Цельсия, F – градусы Фаренгейта.
Какая температура по шкале Фаренгейта
соответствует -43 градусам по шкале
Цельсия?
Ответ
-45,4
23.
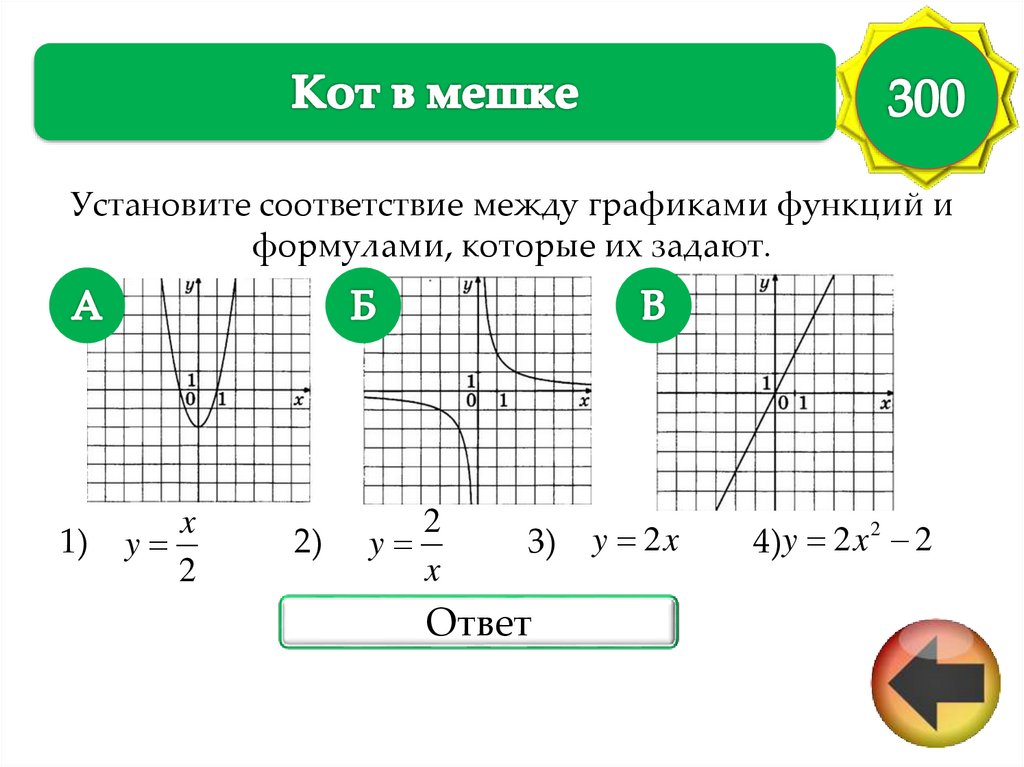
Установите соответствие между графиками функций иформулами, которые их задают.
1)
x
y
2
2)
2
y
x
3)
Ответ
y 2x
2
4)y 2 x 2
24.
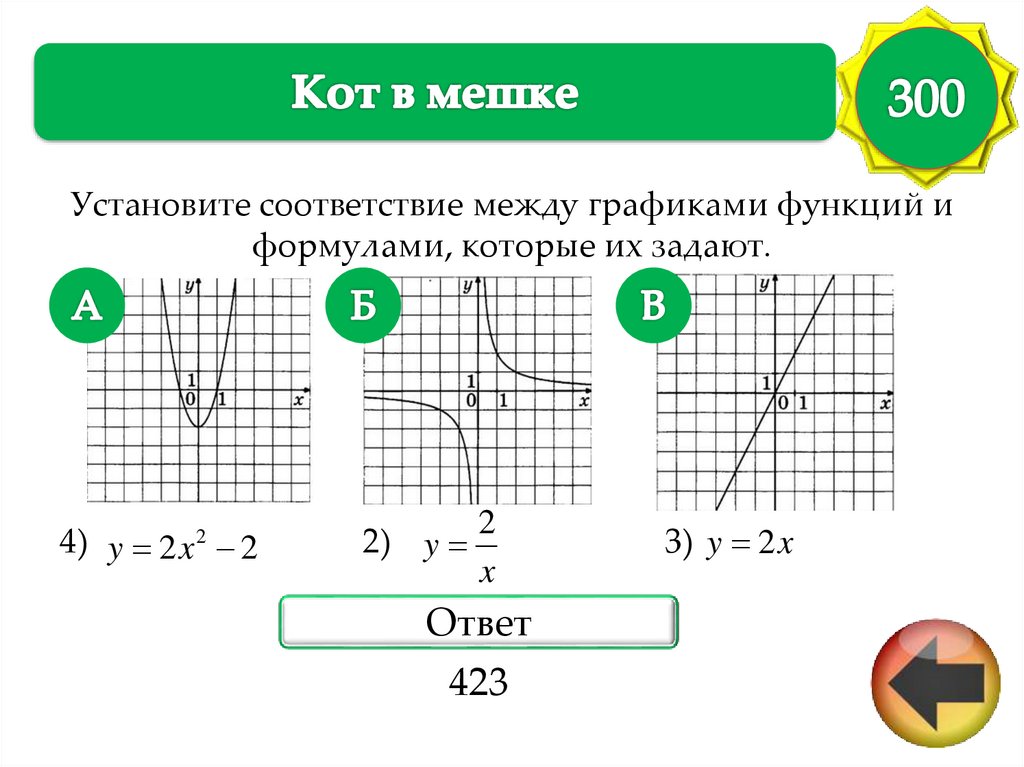
Установите соответствие между графиками функций иформулами, которые их задают.
4) y 2 x 2
2
2
2) y
x
Ответ
423
3) y 2 x
25.
На тарелке лежат одинаковые на видпирожки: 4 с творогом, 3 с мясом и 5 с
яблоками. Ваня наугад берёт один
пирожок. Найдите вероятность того, что
пирожок окажется с мясом.
Ответ
26.
На тарелке лежат одинаковые на видпирожки: 4 с творогом, 3 с мясом и 5 с
яблоками. Ваня наугад берёт один пирожок.
Найдите
вероятность того, что пирожок
окажется с мясом.
Ответ
0,25
27.
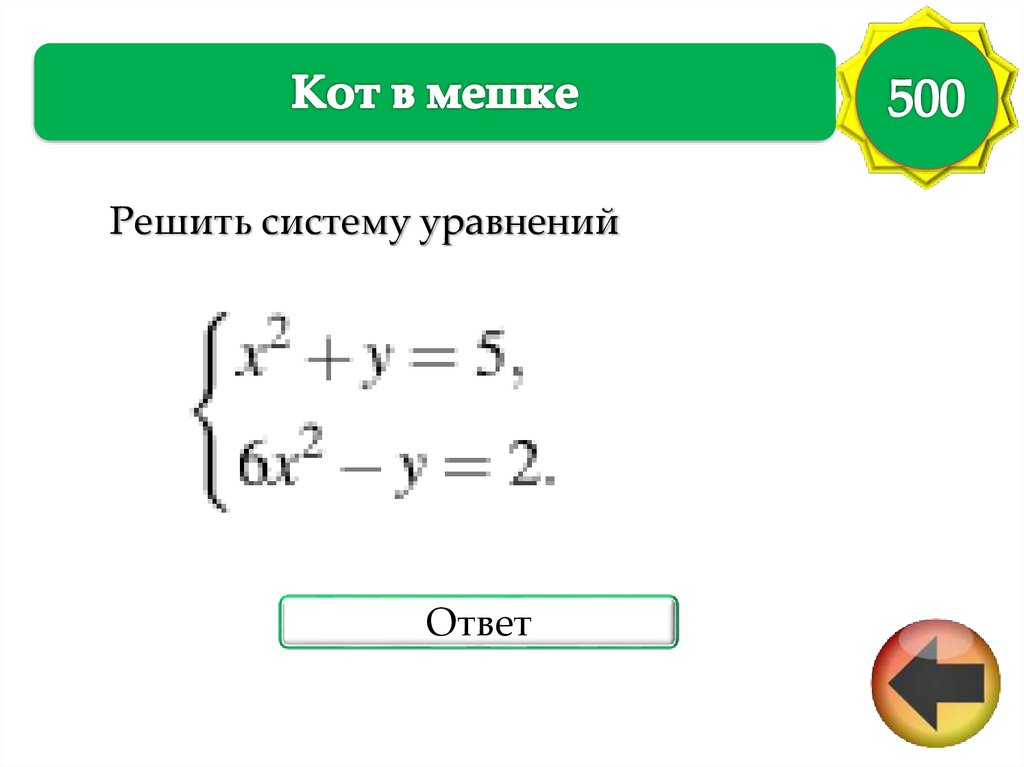
Решить систему уравненийОтвет
28.
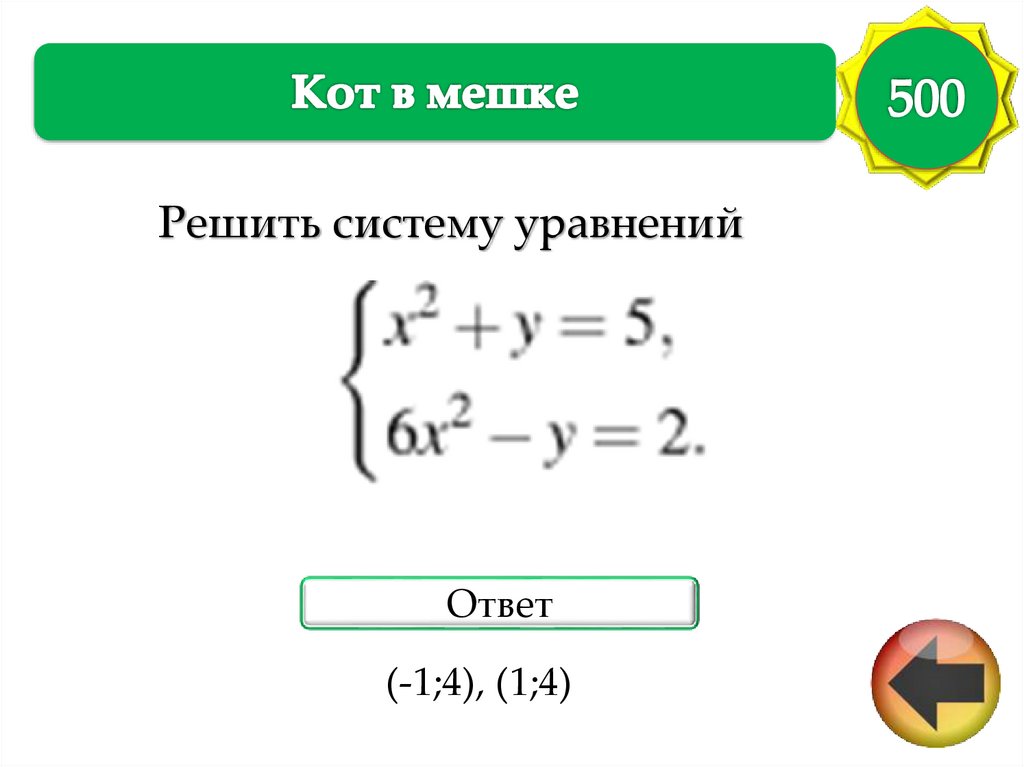
Решить систему уравненийОтвет
(-1;4), (1;4)
29.
В амфитеатре 11 рядов. В первом ряду 24места, а в каждом следующем на 3 места
больше, чем в предыдущем. Сколько мест
в восьмом ряду амфитеатра?
Ответ
30.
В амфитеатре 11 рядов. В первом ряду 24места, а в каждом следующем на 3 места
больше, чем в предыдущем. Сколько мест в
восьмом ряду амфитеатра?
Ответ
45
31.
При проведении опыта вещество равномерноохлаждали в течение 10 минут. При этом
каждую минуту температура вещества
уменьшалась на 6°C. Найдите температуру
вещества (в градусах Цельсия) через 4
минуты после начала проведения опыта, если
его начальная температура составляла -7°C.
Ответ
32.
При проведении опыта вещество равномерноохлаждали в течение 10 минут. При этом
каждую минуту температура вещества
уменьшалась на 6°C. Найдите температуру
вещества (в градусах Цельсия) через 4
минуты после начала проведения опыта, если
его начальная температура составляла -7°C.
Ответ
-31
33.
В ходе биологического эксперимента в чашкуПетри с питательной средой поместили
колонию микроорганизмов массой 13мг. За
каждые 30 минут масса колонии увеличивается
в 3 раза. Найдите массу колонии
микроорганизмов через 90 минут после начала
эксперимента. Ответ дайте в миллиграммах.
Ответ
34.
В ходе биологического эксперимента в чашкуПетри с питательной средой поместили
колонию микроорганизмов массой 13мг. За
каждые 30 минут масса колонии увеличивается
в 3 раза. Найдите массу колонии
микроорганизмов через 90 минут после начала
эксперимента. Ответ дайте в миллиграммах.
Ответ
351
35.
В кафе есть только квадратные столики, за каждый из которых могутсесть 4 человека. Если сдвинуть два квадратных столика, то
получится стол, за который могут сесть 6 человек. На рисунке
изображён случай, когда сдвинули 3 квадратных столика вдоль
одной линии. В этом случае получился стол, за
который могут сесть 8 человек. Сколько человек может сесть за стол,
который получится, если сдвинуть 22 квадратных столика вдоль
одной линии?
Ответ
36.
В кафе есть только квадратные столики, за каждый из которыхмогут сесть 4 человека. Если сдвинуть два квадратных столика, то
получится стол, за который могут сесть 6 человек. На рисунке
изображён случай, когда сдвинули 3 квадратных столика вдоль
одной линии. В этом случае получился стол, за
который могут сесть 8 человек. Сколько человек может сесть за
стол, который получится, если сдвинуть 22 квадратных столика
вдоль одной линии?
Ответ
48
37.
В ходе бета-распада радиоактивного изотопа Акаждые 7 минут половина его атомов без
потери
массы
преобразуются
в
атомы
стабильного изотопа Б. В начальный момент
масса изотопа А составляла 640 мг. Найдите
массу образовавшегося изотопа Б через 42
минуты. Ответ дайте в миллиграммах.
Ответ
38.
В ходе бета-распада радиоактивного изотопа Акаждые 7 минут половина его атомов без
потери
массы
преобразуются
в
атомы
стабильного изотопа Б. В начальный момент
масса изотопа А составляла 640 мг. Найдите
массу образовавшегося изотопа Б через 42
минуты. Ответ дайте в миллиграммах.
Ответ
10
39.
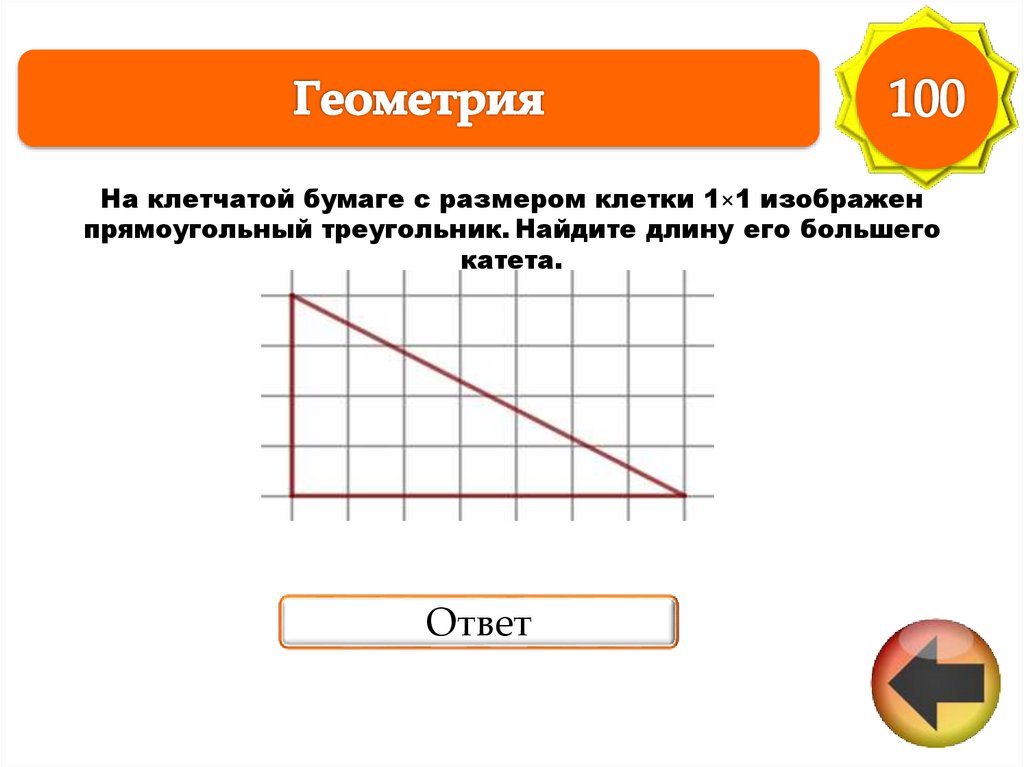
На клетчатой бумаге с размером клетки 1×1 изображенпрямоугольный треугольник. Найдите длину его большего
катета.
Ответ
40.
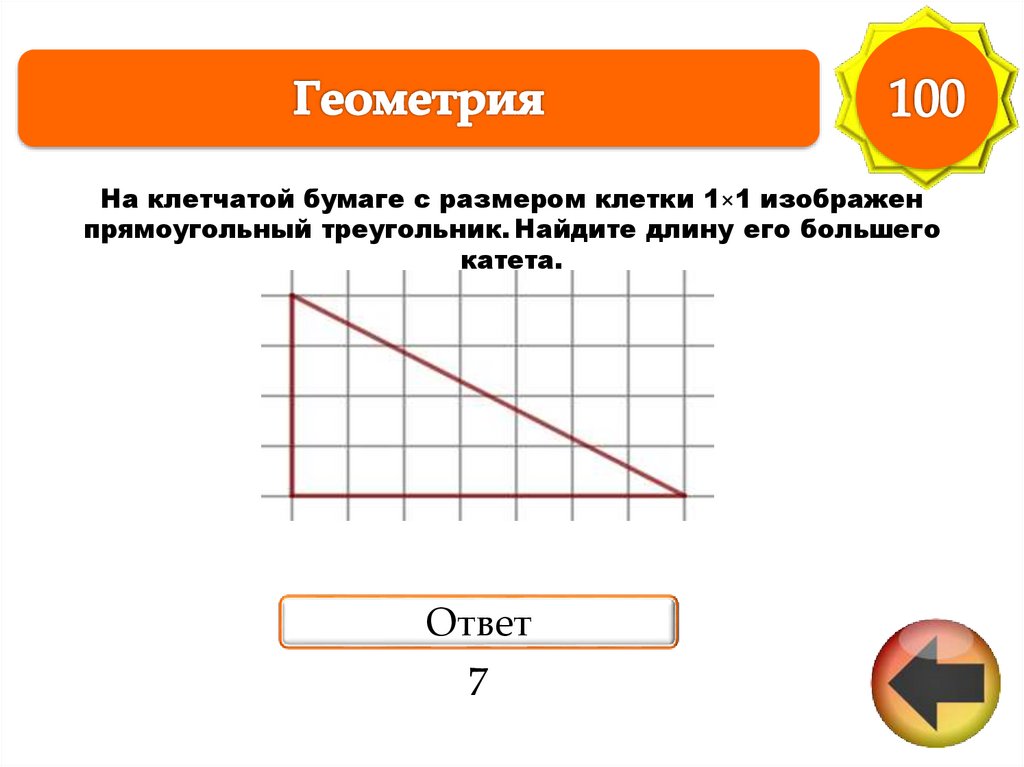
На клетчатой бумаге с размером клетки 1×1 изображенпрямоугольный треугольник. Найдите длину его большего
катета.
Ответ
7
41.
Какое из следующих утверждений верно?1) Если три угла одного треугольника равны
соответственно трём углам другого
треугольника, то такие треугольники равны
2) Любой квадрат является прямоугольником.
3) Каждая из биссектрис равнобедренного
треугольника является его высотой.
Ответ
42.
Какие из следующих утверждений верны?1) Если три угла одного треугольника равны
соответственно трём углам другого
треугольника, то такие треугольники равны
2) Любой квадрат является прямоугольником.
3) Каждая из биссектрис равнобедренного
треугольника является его высотой.
Ответ
2
43.
Два угла ромба относятся как 3 : 7.Найдите больший угол. Ответ дайте в
градусах.
Ответ
44.
Два угла ромба относятся как 3 : 7.Найдите больший угол. Ответ дайте в
градусах.
Ответ
126
45.
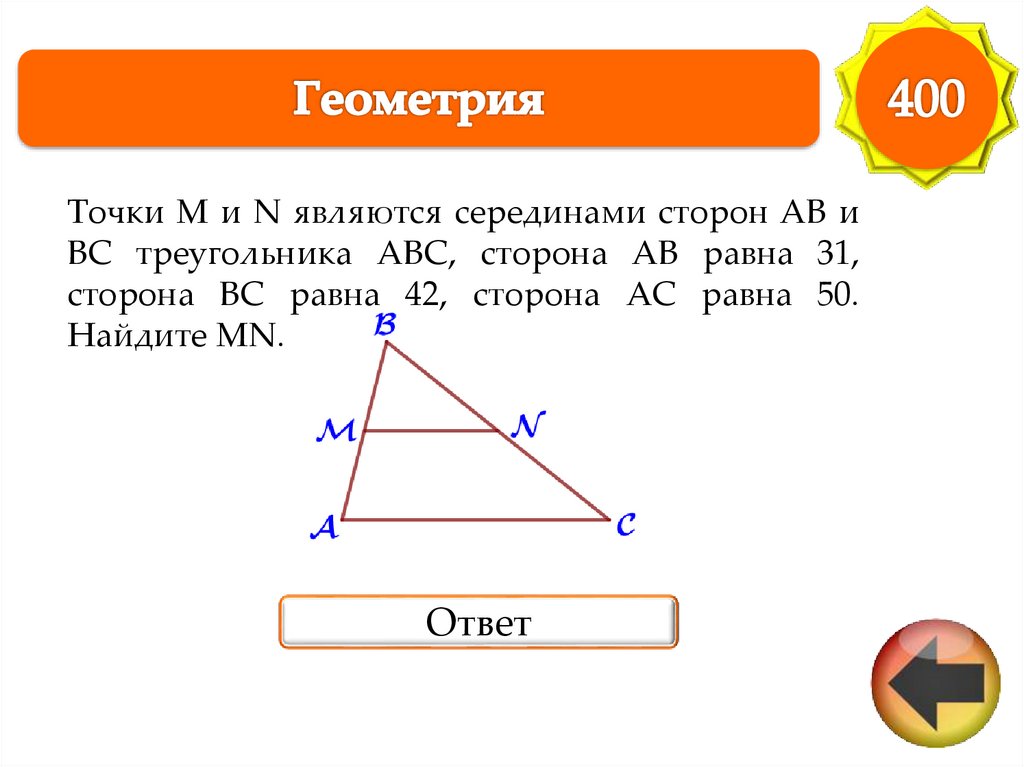
Точки M и N являются серединами сторон AB иBC треугольника ABC, сторона AB равна 31,
сторона BC равна 42, сторона AC равна 50.
Найдите MN.
Ответ
46.
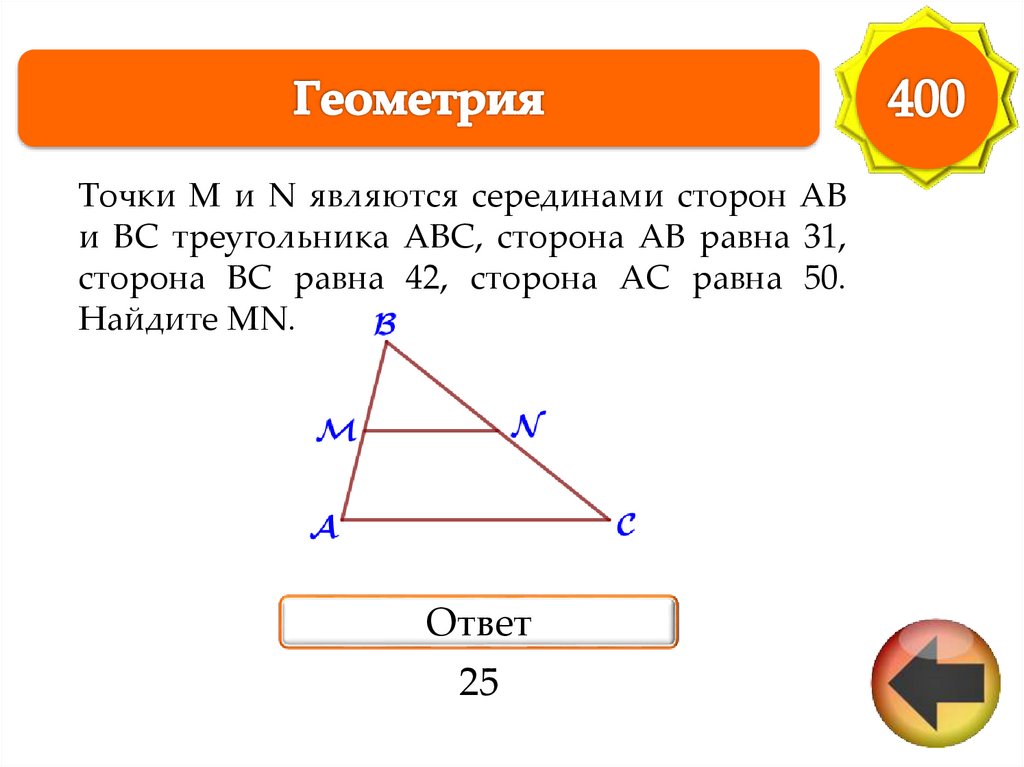
Точки M и N являются серединами сторон ABи BC треугольника ABC, сторона AB равна 31,
сторона BC равна 42, сторона AC равна 50.
Найдите MN.
Ответ
25
47.
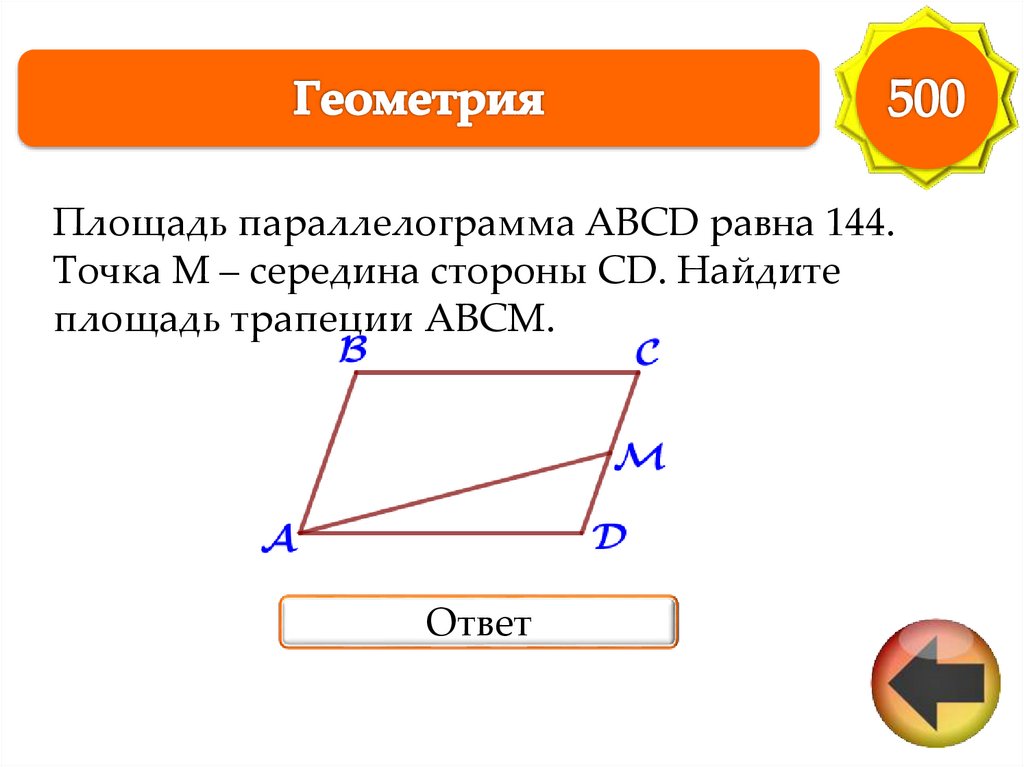
Площадь параллелограмма ABCD равна 144.Точка M – середина стороны CD. Найдите
площадь трапеции ABCM.
Ответ
48.
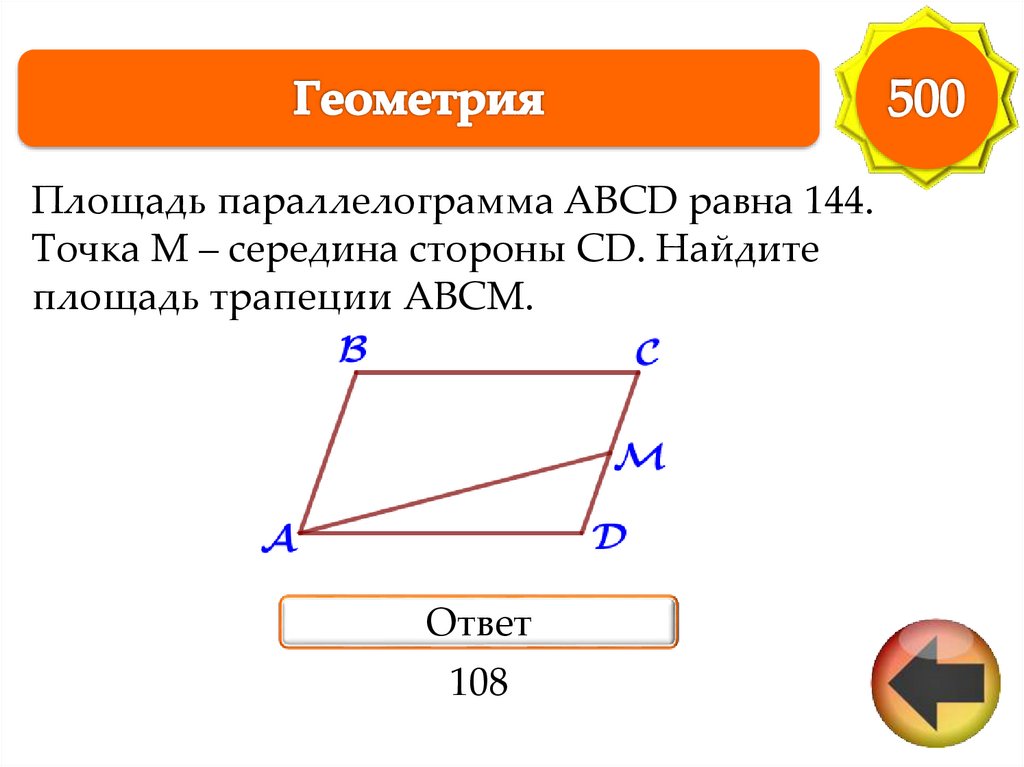
Площадь параллелограмма ABCD равна 144.Точка M – середина стороны CD. Найдите
площадь трапеции ABCM.
Ответ
108
49.
Найдите корень уравнения x2 - 5x - 50=0 .Если уравнение имеет более одного корня,
в ответе укажите больший из них.
Ответ
50.
Найдите корень уравнения x2 - 5x -50=0 .Если уравнение имеет более одного корня, в
ответе укажите больший из них.
Ответ
10
51.
Найдите корень уравнения(x +9)(-x +8)= 0 . Если уравнение имеет
более одного корня, в ответе укажите
меньший из них.
Ответ
52.
Найдите корень уравнения(x +9)(-x +8)= 0 . Если уравнение имеет
более одного корня, в ответе укажите
меньший из них.
Ответ
-9
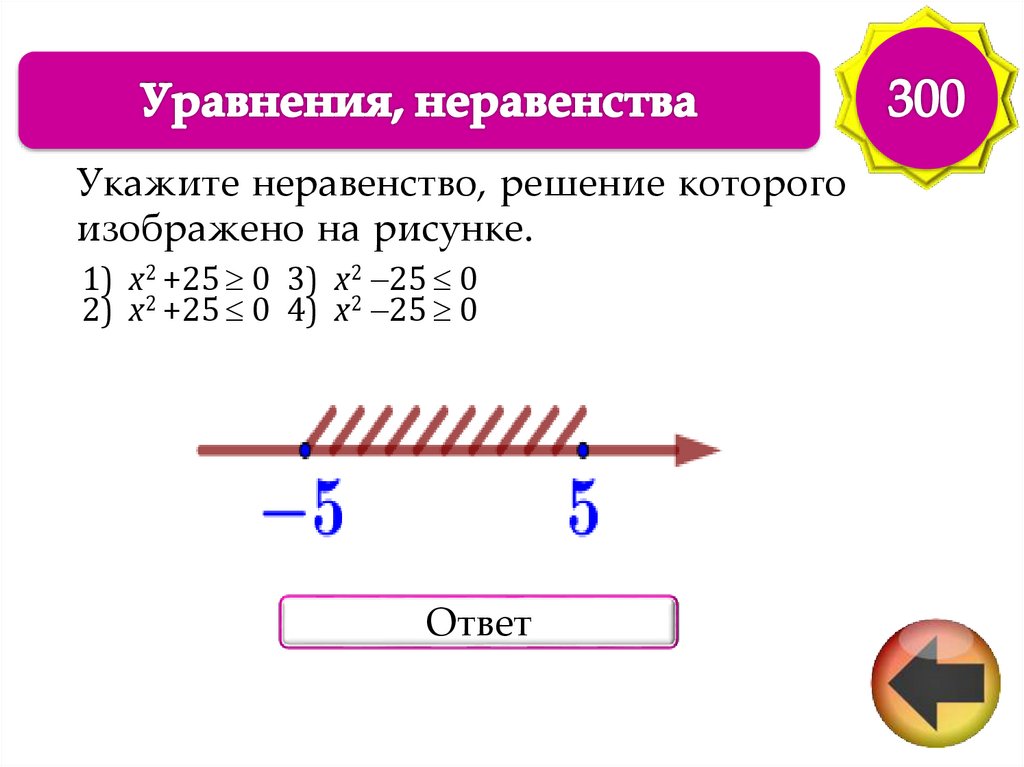
53.
Укажите неравенство, решение которогоизображено на рисунке.
1) x2 +25 0 3) x2 25 0
2) x2 +25 0 4) x2 25 0
Ответ
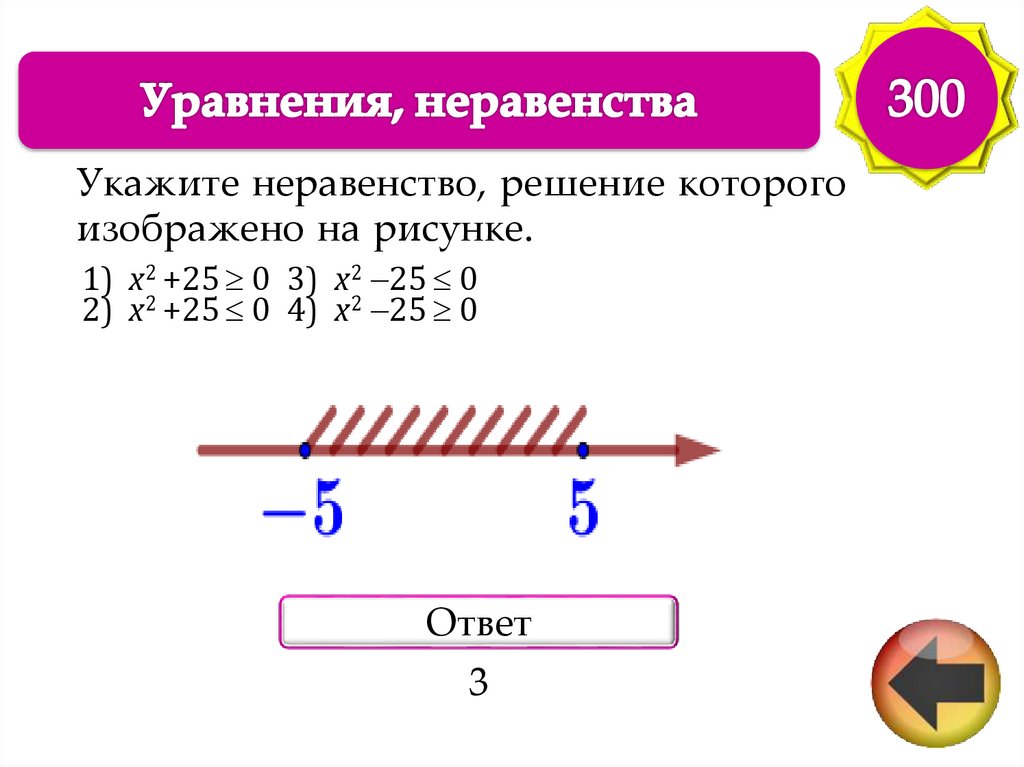
54.
Укажите неравенство, решение которогоизображено на рисунке.
1) x2 +25 0 3) x2 25 0
2) x2 +25 0 4) x2 25 0
Ответ
3
55.
Решите уравнениеx3 +5x2 = 4x +20
Ответ
56.
Решите уравнениеx3 +5x2 = 4x +20
Ответ
-5, -2, 2
57.
Решите уравнениеx2 6x +
=
+27
Ответ
58.
Решите уравнениеx2 6x +
=
+27
Ответ
-3