Презентация по теме _Математическое ожидание слуайной велиины_ 9 класс

1. 70. Математическое ожидание случайной величины

Вероятность и статистика
9 класс

2. Математическим ожиданием

Значение Х
…
Вероятность
…

3. Пример

• Для проведения лотереи изготовили
100 билетов. Из них 1 билет с
выигрышем в 500 руб., 10 билетов – по
100 руб., остальные билеты – без
выигрыша. Какой средний выигрыш
соответствует одному билету?
• Решение. Выигрыш – случайная
величина Х, которая принимает
значения 0, 100, 500.

4. Для проведения лотереи изготовили 100 билетов. Из них 1 билет с выигрышем в 500 руб., 10 билетов – по 100 руб., остальные

билеты – без выигрыша. Какой средний
выигрыш соответствует одному билету?
Случайная
величина Х
0
100
500
Вероятность
0,89
0,1
0,01
Если купить все 100 билетов, то выигрыш – 1500 руб.
Выигрыш одного билета – 1500:100=15 руб. – среднее значение
случайной величины.
Или
0∙0,89+100∙0,1+500∙0,01=15=М(Х) – математическое ожидание

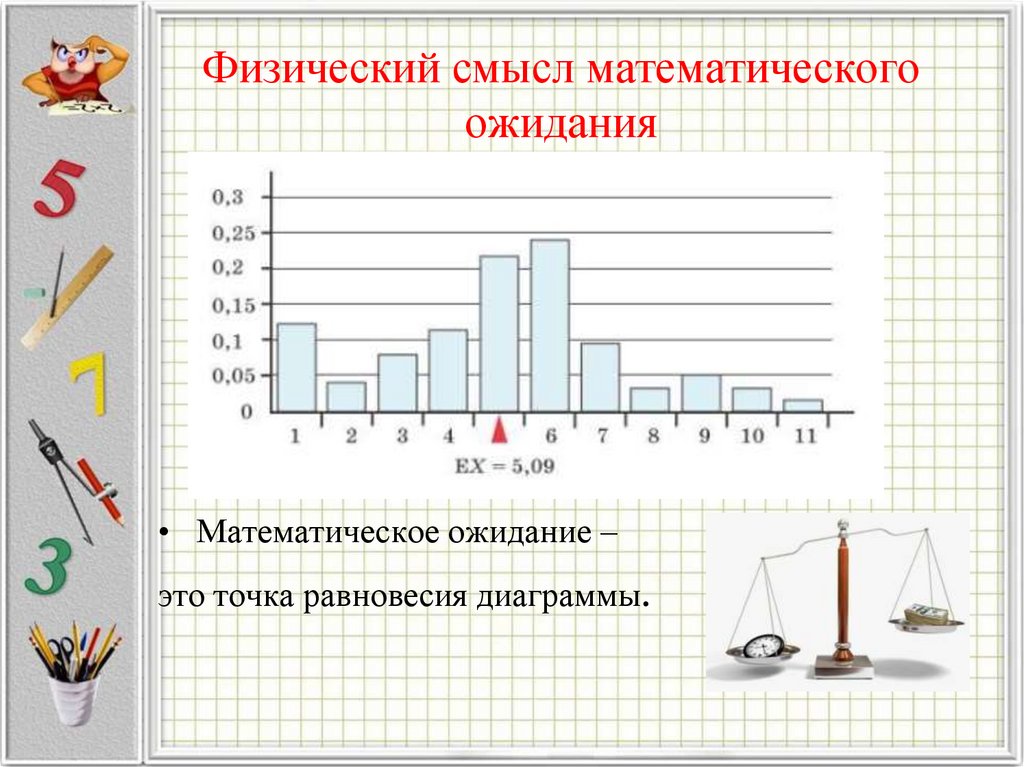
5. Физический смысл математического ожидания

• Математическое ожидание –
это точка равновесия диаграммы.

6. Пример «Лотерея»

• В лотерее должны быть большие выигрыши для
того, чтобы она была привлекательной . Пусть 1%
билетов с выигрышем в 2000 р. Выигрышных
билетов должно быть немало. Пусть 10% билетов с
выигрышем по 200 р. Участник лотереи случайным
образом выигрывает один билет. Найдем
математическое ожидание случайной величины Х
«выигрыш участника».
• Решение. Случайная величина Х принимает
значения 0, 200, 2000. Найдем соответствующие
этим значениям вероятности.

7. Математическое ожидание выигрыша М(Х)=0∙0,89+200∙0,1+2000∙0,01=40 руб. Чтобы лотерея принесла доход, цена билета должна быть

Выигрыш,
руб.
0
200
2000
Вероятность
выигрыша
0,89
0,1
0,01
Математическое ожидание выигрыша
М(Х)=0∙0,89+200∙0,1+2000∙0,01=40 руб.
Чтобы лотерея принесла доход, цена билета должна
быть больше, чем средний выигрыш.
Если назначить цену билета 50 руб., то средний доход
от продажи одного билета 50-40=10 руб.

8. Пример

• В лотерее 100 билетов, из которых 2
выигрышных по 110 руб. и 10 билетов
выигрышных по 20 руб. Стоимость
билета 10 руб. Х- чистый выигрыш для
человека, купившего один билет.
Найти математическое ожидание
случайной величины Х «выигрыш
участника». Данные запишите в
таблицу.

9. Составим таблицу

Выигрыш,
руб.
0
20
110
Вероятность
выигрыша
0,88
0,1
0,02
• М(Х)=0∙0,88+20∙0,1+110∙0,02=4,2 руб. –
это математическое ожидание
выигрыша.
• Стоимость билета 10 руб. Значит, мы
переплачиваем 10-4,2=5,8 руб. с
каждого билета.

10. Пример «Страхование»

• Стоимость страхового полиса – это
сумма математического ожидания
страховой выплаты (например, при
ДТП) и доли, идущей в доход
страховой компании (зар. плата
сотрудников, аренда и содержание
офиса, налоги и пр.).

11. Пример «Страхование»

• В страховой компании застраховано 10 тыс.
человек. Каждый застрахованный
выплачивает в год 1 тыс. руб. Вероятность
наступления страхового случая в течении
года для одного застрахованного 0,01.
Выплата при наступлении страхового
случая равна 50 тыс. руб. Найти прибыль
страховой компании за год.
• Решение. Пусть Х- прибыль страховой
компании за год.

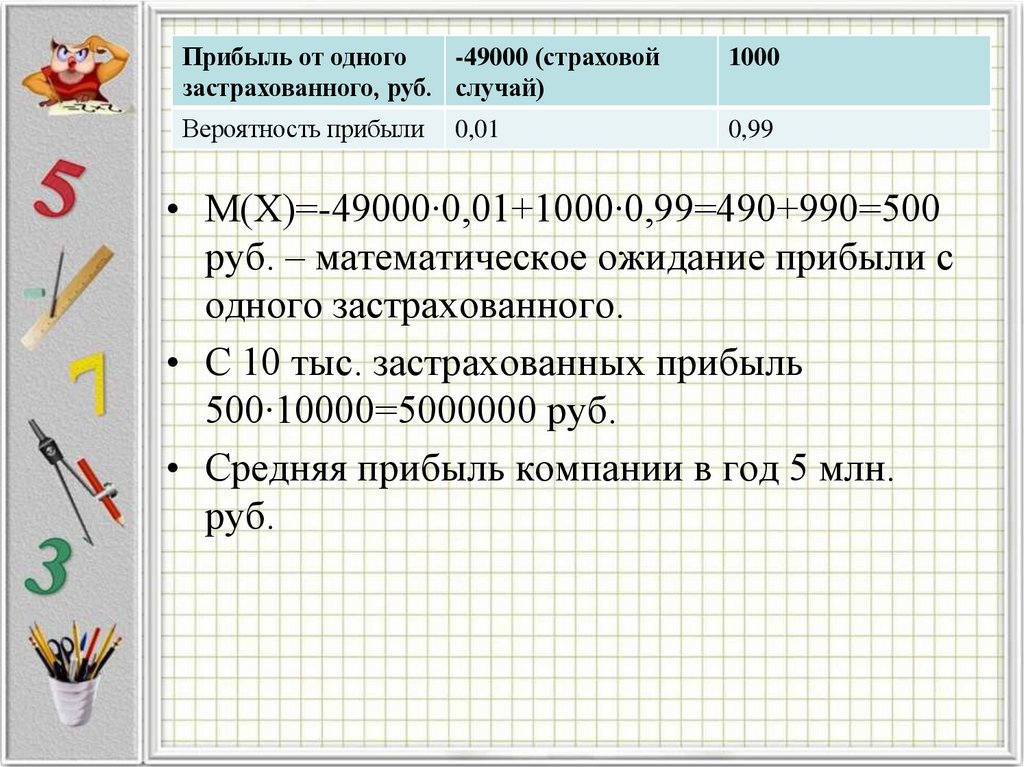
12.

Прибыль от одного
-49000 (страховой
застрахованного, руб. случай)
1000
Вероятность прибыли
0,99
0,01
• М(Х)=-49000∙0,01+1000∙0,99=490+990=500
руб. – математическое ожидание прибыли с
одного застрахованного.
• С 10 тыс. застрахованных прибыль
500∙10000=5000000 руб.
• Средняя прибыль компании в год 5 млн.
руб.

13. Решить самостоятельно

• В лотереи участвуют 10 тыс. билетов.
Цена каждого билета 50 руб. Известно,
что 1000 билетов дают выигрыш в 100
руб., 10 билетов – выигрыш в 1000
руб., 1 билет – выигрыш 10 тыс. руб.
Остальные билеты без выигрыша.
Найти математическое ожидание
случайной величины «выигрыш на
один случайный лотерейный билет».