Похожие презентации:
Математическое ожидание
1.
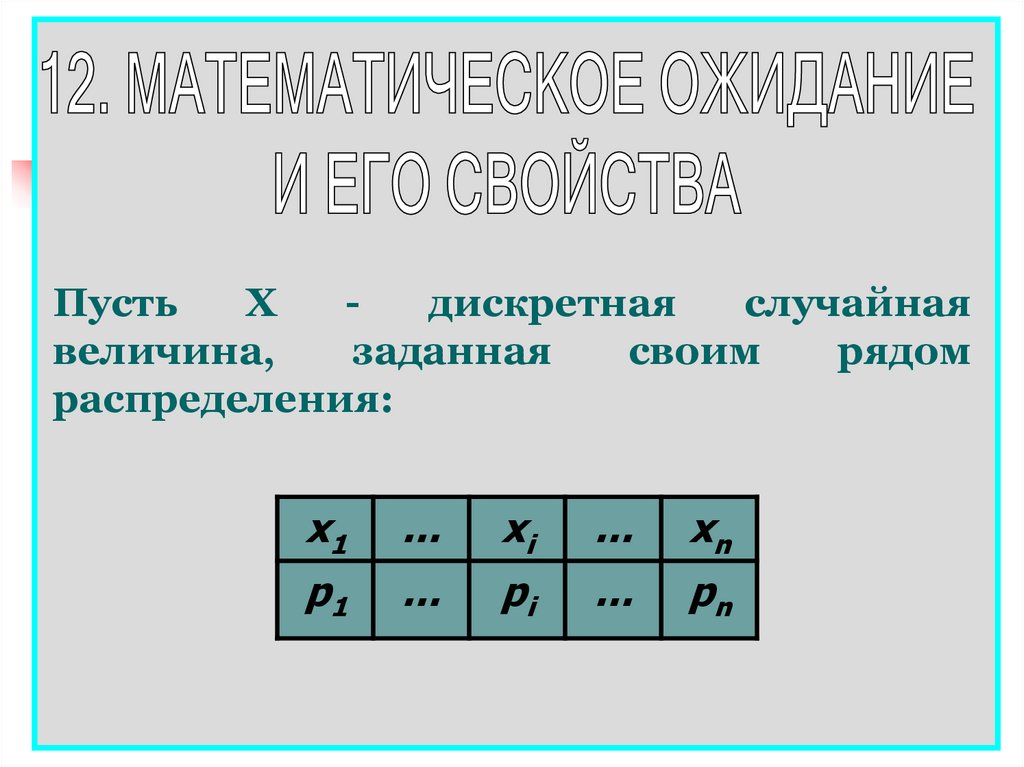
ПустьХ
дискретная
случайная
величина,
заданная
своим
рядом
распределения:
x1
…
xi
…
xn
p1
…
pi
…
pn
2.
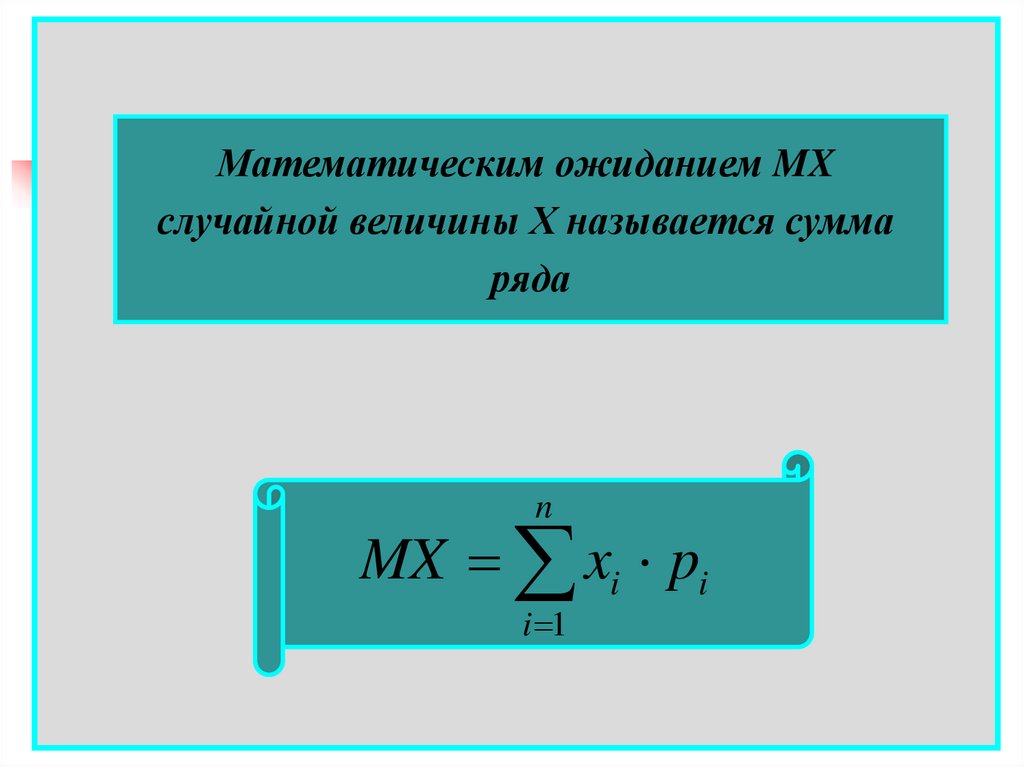
Математическим ожиданием MXслучайной величины Х называется сумма
ряда
n
MX xi pi
i 1
3.
Пример Х –число очков приоднократном бросании игральной
кости МХ-?
4.
Пример Х –число очков приоднократном бросании игральной
кости МХ-?
х
р
1
2
3
4
5
6
1/6 1/6 1/6 1/6 1/6 1/6
1
1
1
1
1
1
MX 1 2 3 4 5 6
6
6
6
6
6
6
1 7
21 3.5
6 2
Если многократно бросить игральную кость и вычислить
среднее число очков, получим число очень близкое к 3.5
5.
В лотерее 100 билетов, из которых 2выигрышных по 110 руб. и 10 выигрышных по 20
руб. Стоимость билета 10 руб. Х - чистый
выигрыш для человека, купившего 1 билет.
МХ-?
6.
В лотерее 100 билетов, из которых 2выигрышных по 110 руб. и 10 выигрышных по 20
руб. Стоимость билета 10 руб. Х - чистый
выигрыш для человека, купившего 1 билет.
МХ-?
х
100
10
-10
р
0,02
0,1
0,88
MX 100 0.02 10 0.1 10 0.88 2 1 8.8 5.8
При многократной покупке билетов на таких условиях
будем терять в среднем 5,8 рубля на билете.
7.
Среднее арифметическое значений,принимаемых случайной величиной в
длинной серии опытов, приближенно
равно ее математическому ожиданию.
8.
Игрок бросает 2 игральные кости.Если на костях выпадает разное число
очков, то он проигрывает а рублей, а если
одинаковое , то выигрывает 4а рублей.
Стоит ли играть в эту игру многократно?
9.
Пусть X – выигрыш игрока в одной игре.X может принимать значения -а и 4а.
10.
Пусть X – выигрыш игрока в одной игре.X может принимать значения -а и 4а.
6 1
P ( X 4a )
36 6
5
P( X a)
6
11.
Пусть X – выигрыш игрока в одной игре.X может принимать значения -а и 4а.
1
P ( X 4a )
6
X
P
4a
5
P( X a)
6
-a
1
6
5
6
12.
Пусть X – выигрыш игрока в одной игре.X может принимать значения -а и 4а.
X
P
4a
-a
1
6
5
6
1
5 4a 5a
a
MX 4a ( a)
0
6
6
6
6
13.
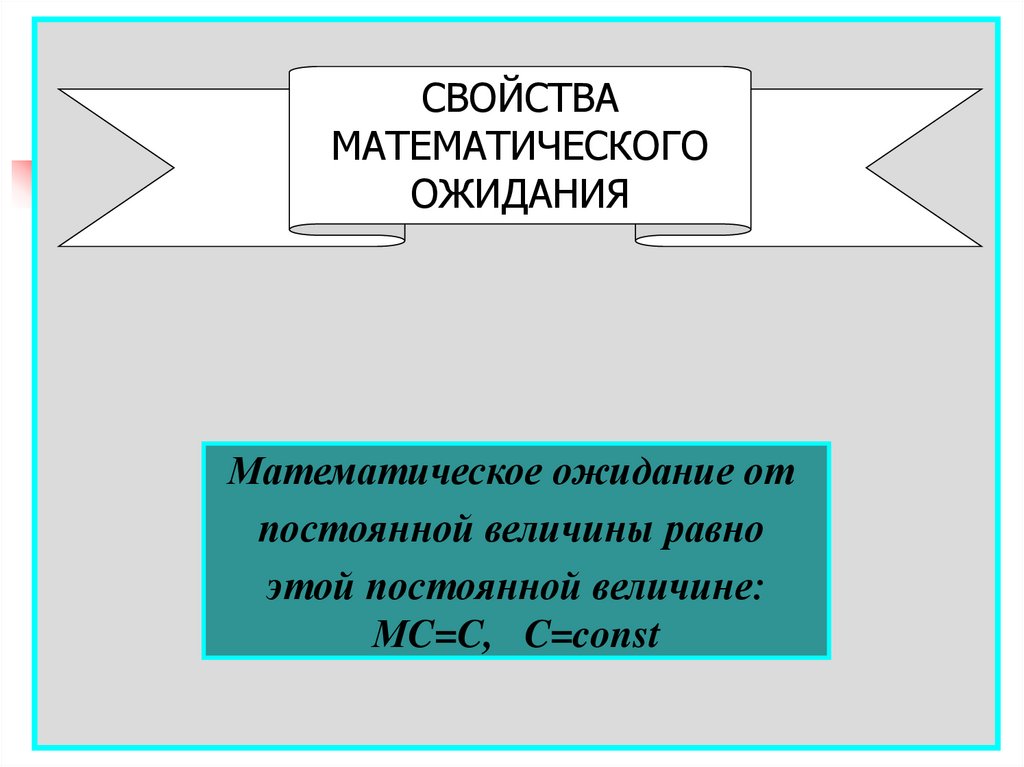
СВОЙСТВАМАТЕМАТИЧЕСКОГО
ОЖИДАНИЯ
Математическое ожидание от
постоянной величины равно
этой постоянной величине:
МC=C, C=const
14.
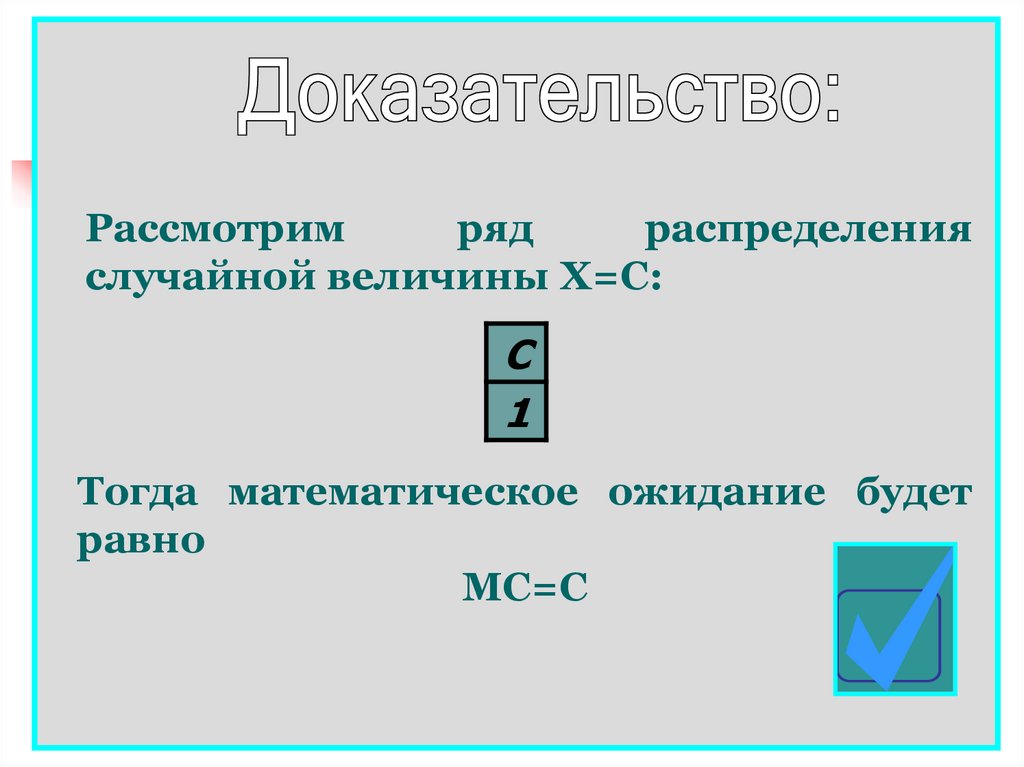
Рассмотримряд
распределения
случайной величины Х=С:
С
1
Тогда математическое ожидание будет
равно
МC=C
15.
Математическое ожидание суммыслучайных величин Х и У равно
сумме математических ожиданий
этих величин:
М(X+Y)=MX+MY
16.
Постоянную величину можновыносить за знак математического
ожидания:
М(с X)=с MX, где с=cоnst.
17.
Математическое ожиданиепроизведения
независимых случайных величин
Х и Y равно произведению
математических ожиданий этих
величин:
М(XY)=MX MY
18.
Пример. Приобретено 40 лотерейных билетов.Вероятность выигрыша на один билет равна
0,05.
Найти математическое ожидание числа
выигравших билетов.
19.
5Пусть X – число выигравших билетов.
1, åñëè i é áèëåò âû èãðàë
Xi
0, åñëè i é áèëåò í å âû èãðàë
X X1 X 2
X 40
20.
Пусть X – число выигравших билетов.1, åñëè i é áèëåò âû èãðàë
Xi
0, åñëè i é áèëåò í å âû èãðàë
X X1 X 2
X 40
MX M ( X1 X 2
MX1 MX 2
X 40 )
MX 40
21.
1, åñëè i é áèëåò âû èãðàëXi
0, åñëè i é áèëåò í å âû èãðàë
Xi
1
0
P
0,05
0,95
MX i 1 0,05 0 0,95 0,05
22.
Пусть X – число выигравших билетов.MX MX 1 MX 2
0,05 0,05
MX 40
0,05 40 0,05 2
23.
Пример. В страховой компании застраховано10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность
наступления страхового случая в течение года
для одного застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Найти MX.
24.
Пример. В страховой компании застраховано10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность
наступления страхового случая в течение года
для одного застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Найти MX.
Xi
- прибыль от i-го застрахованного,
i=1,2…10000
X X1 X 2
X 10000
MX MX 1 MX 2
MX 10000
25.
Пример. В страховой компании застраховано10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность
наступления страхового случая в течение года
для одного застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Найти MX.
- прибыль от i-го застрахованного,
i=1,2…10000
Xi
Xi
-49000
1000
P
0,01
0,99
MX i 49000 0,01 1000 0,99 500
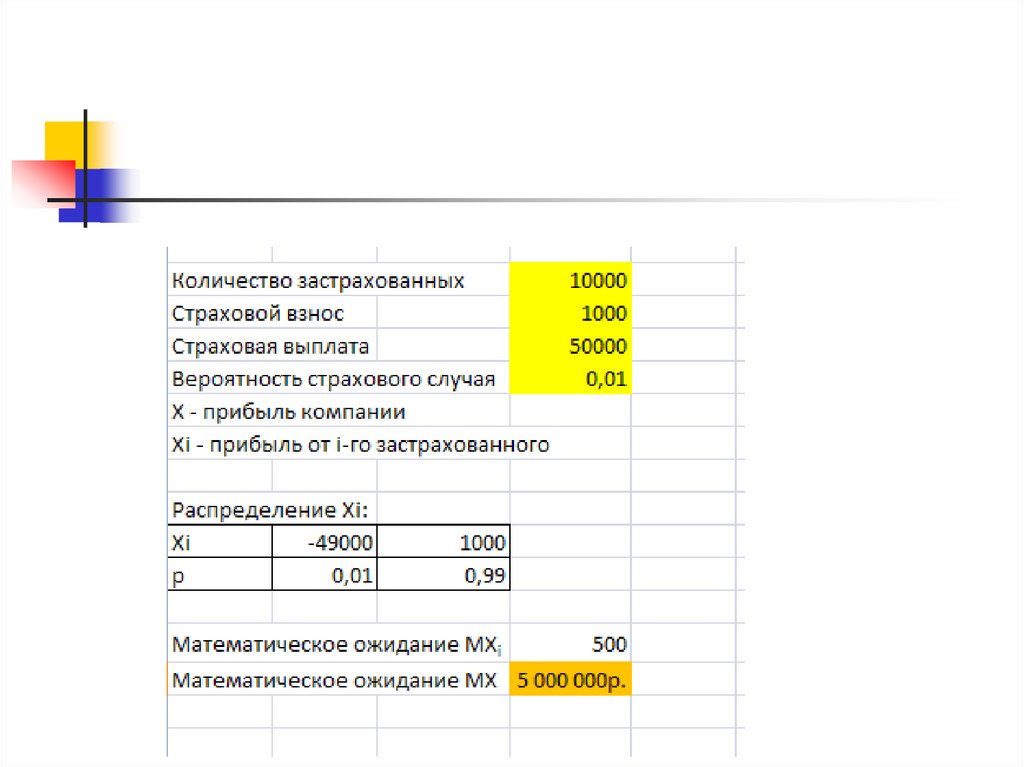
26.
Пример. В страховой компании застраховано10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность
наступления страхового случая в течение года
для одного застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Найти MX.
прибыль от i-го застрахованного,
X i -i=1,2…10000
MX i 500
MX MX 1 MX 2
MX 10000 500 10000 5 000 000
Средняя прибыль компании в год составит 5 млн рублей
27.
28.
Пример. В страховой компании застраховано10 тысяч человек. Вероятность наступления
страхового случая в течение года для одного
застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Каким должен быть страховой взнос s,
чтобы средняя прибыль компании была не
меньше 10 млн. руб?
29.
Пример. В страховой компании застраховано10 тысяч человек. Вероятность наступления
страхового случая в течение года для одного
застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Каким должен быть страховой взнос s,
чтобы средняя прибыль компании была не
меньше 10 млн. руб?
Xi
- прибыль от i-го застрахованного,
i=1,2…10000
X X1 X 2
X 10000
MX MX 1 MX 2
MX 10000
30.
Пример. В страховой компании застраховано10 тысяч человек. Вероятность наступления
страхового случая в течение года для одного
застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Каким должен быть страховой взнос s,
чтобы средняя прибыль компании была не
меньше 10 млн. руб?
X i - прибыль от i-го застрахованного,
i=1,2…10000
Xi
P
-50000+s
s
0,01
0,99
MX i ( 50000 s ) 0,01 s 0,99
500 0.01s 0.99s 500 s
31.
Пример. В страховой компании застраховано10 тысяч человек. Вероятность наступления
страхового случая в течение года для одного
застрахованного 0,01. Выплата при
наступлении страхового случая равна 50 тыс.
рублей. Пусть X – прибыль страховой компании
за год. Каким должен быть страховой взнос s,
чтобы средняя прибыль компании была не
меньше 10 млн. руб?
MX 10000( 500 s)
MX 10 000 000
10000( 500 s) 10 000 000
500 s 1000
s 1500
Страховой взнос должен быть не меньше 1500 рублей


























 Математика
Математика








