Т.1.Л.1.2

1.

Мореходная астрономия
кафедра Навигации

2.

Тема лекции, вопросы
Тема 1. Небесная сфера, сферические координаты
1. Основные формулировки и определения
2. Системы координат
3. Параллактический треугольник, его решение
4. Графическое решение астрономических задач
2

3.

Учебная цель, воспитательная цель
I. Учебная цель: Дать представление о небесной сфере и
сферических координатах
II. Воспитательная цель: Сформировать у курсантов
чувство ответственности, значимости за будущую
специальность
3

4.

РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ
И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
4
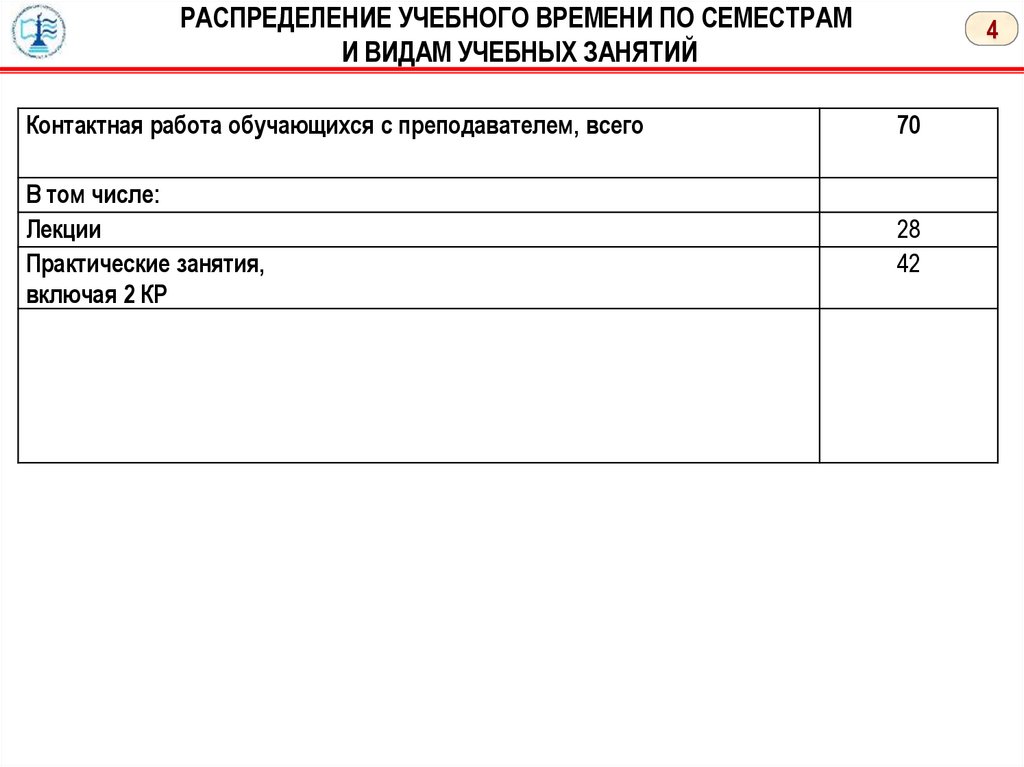
Контактная работа обучающихся с преподавателем, всего
70
В том числе:
Лекции
Практические занятия,
включая 2 КР
28
42

5.

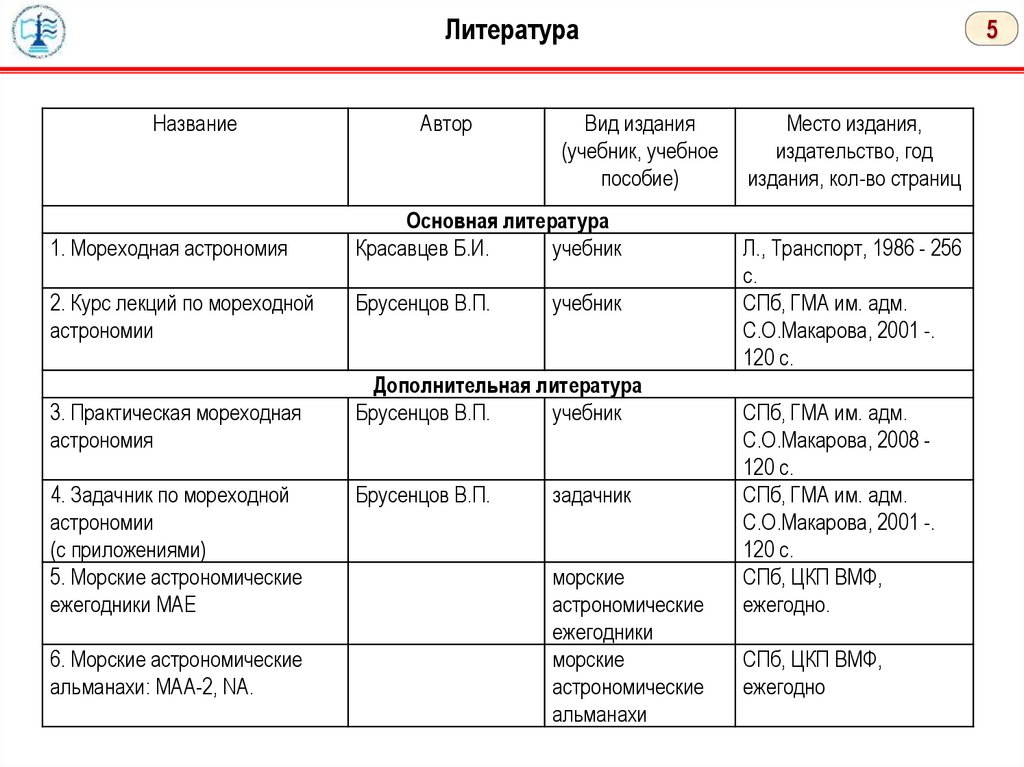
Литература
Название
1. Мореходная астрономия
2. Курс лекций по мореходной
астрономии
3. Практическая мореходная
астрономия
4. Задачник по мореходной
астрономии
(с приложениями)
5. Морские астрономические
ежегодники МАЕ
6. Морские астрономические
альманахи: МАА-2, NA.
Автор
Вид издания
(учебник, учебное
пособие)
Основная литература
Красавцев Б.И.
учебник
Брусенцов В.П.
учебник
Дополнительная литература
Брусенцов В.П.
учебник
Брусенцов В.П.
задачник
морские
астрономические
ежегодники
морские
астрономические
альманахи
5
Место издания,
издательство, год
издания, кол-во страниц
Л., Транспорт, 1986 - 256
с.
СПб, ГМА им. адм.
С.О.Макарова, 2001 -.
120 с.
СПб, ГМА им. адм.
С.О.Макарова, 2008 120 с.
СПб, ГМА им. адм.
С.О.Макарова, 2001 -.
120 с.
СПб, ЦКП ВМФ,
ежегодно.
СПб, ЦКП ВМФ,
ежегодно

6.

Кодекс ПДНВ
6
Требования к судоводителю:
1. Уметь определять место судна по небесным светилам
2. Уметь определять поправки гиро- и магнитных компасов с использованием
средств мореходной астрономии
Подготовка включает:
1. Настройка и работа с секстаном
2. Исправление высот светил
3. Расчёт наступления верхней кульминации Солнца
4. Расчёт широты по Полярной и по Солнцу
5. Прокладка линий положения и определение места судна
6. Определение времени восхода/захода Солнца
7. Выбор светил для измерений в навигационные сумерки
8. Определение поправки компаса

7.

1. Основные формулировки и определения
7
Мореходная астрономия (морская астронавигация) – это часть
практической астрономии, рассматривающая ориентировку по
небесным светилам во времени, по месту и направлению при
движении на море.
Основными задачами мореходной астрономии являются:
– определение места судна в море по небесным светилам;
– определение истинных направлений относительно наблюдаемых
небесных светил (определение «ΔК»);
– определение, хранение и распространение точного времени;
– оценка естественной освещенности и астронавигационной обстановки
в районе плавания.
«Астрономия» – слово греческое («астрон» – звезда и «номос» –
закон), которое можно перевести как – «учение о звездных законах»
или «наука о небесных светилах».

8.

1. Основные формулировки и определения
8
В руководящих документах для мореплавателей даны описания
160 звезд, практика астрономического ориентирования показывает, что
наблюдения обеспечиваются 25-30 звездами.
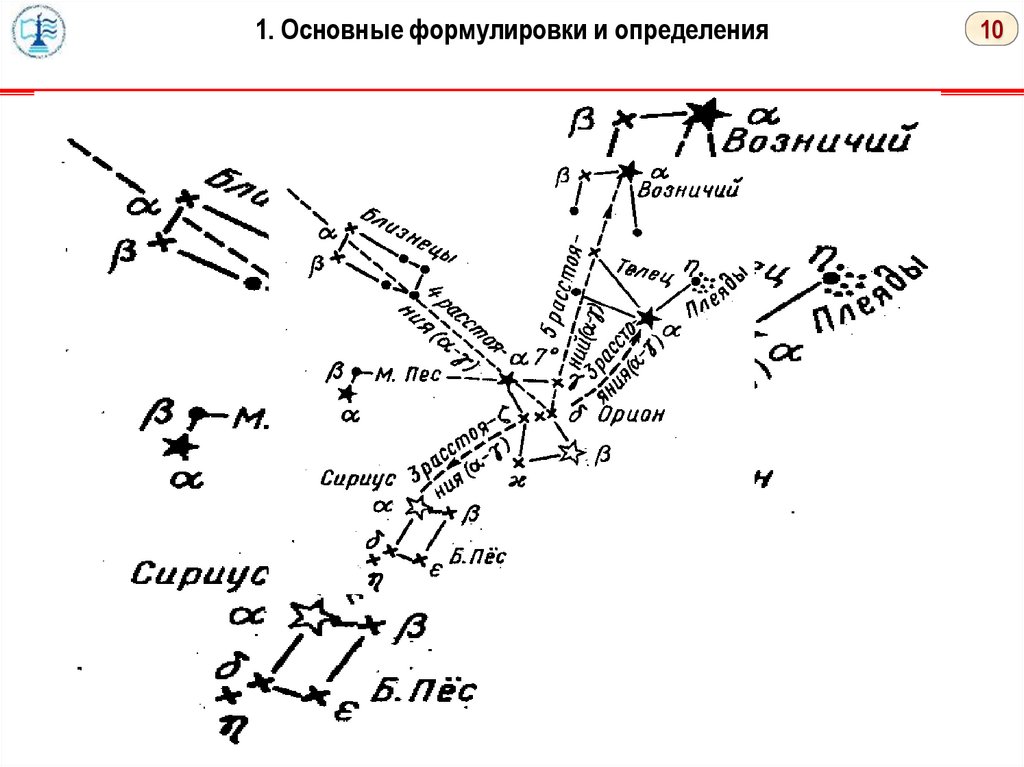
Существует 3 способа опознавания звезд:
1. По характерному расположению светил в созвездиях;
2. По яркости звезды;
3. По цвету.
В настоящее время небо поделено 88 участков, наиболее яркие
звезды, в которых обозначены буквами латинского алфавита в порядке
убывания и также имеют собственные имена.
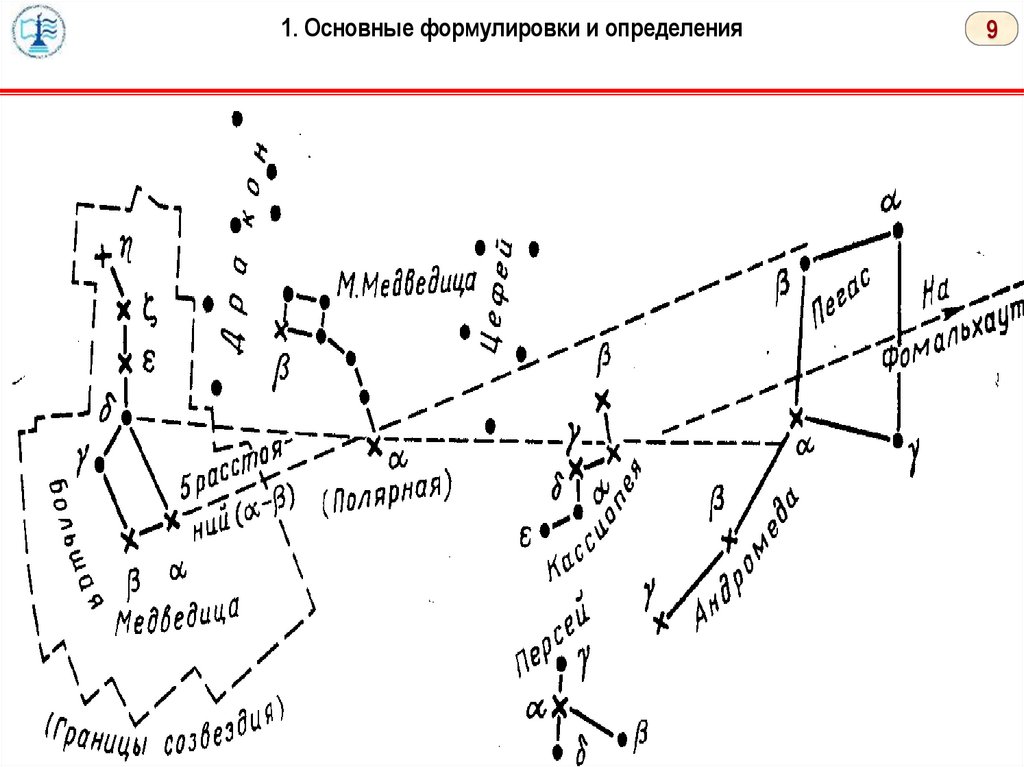
В северных широтах ориентирование по звездам удобнее всего
начинать с отыскания на северной половине неба известного всем
созвездия Большой медведицы напоминающего по форме очертание
ковша.

9.

1. Основные формулировки и определения
9

10.

1. Основные формулировки и определения
10

11.

1. Основные формулировки и определения
11
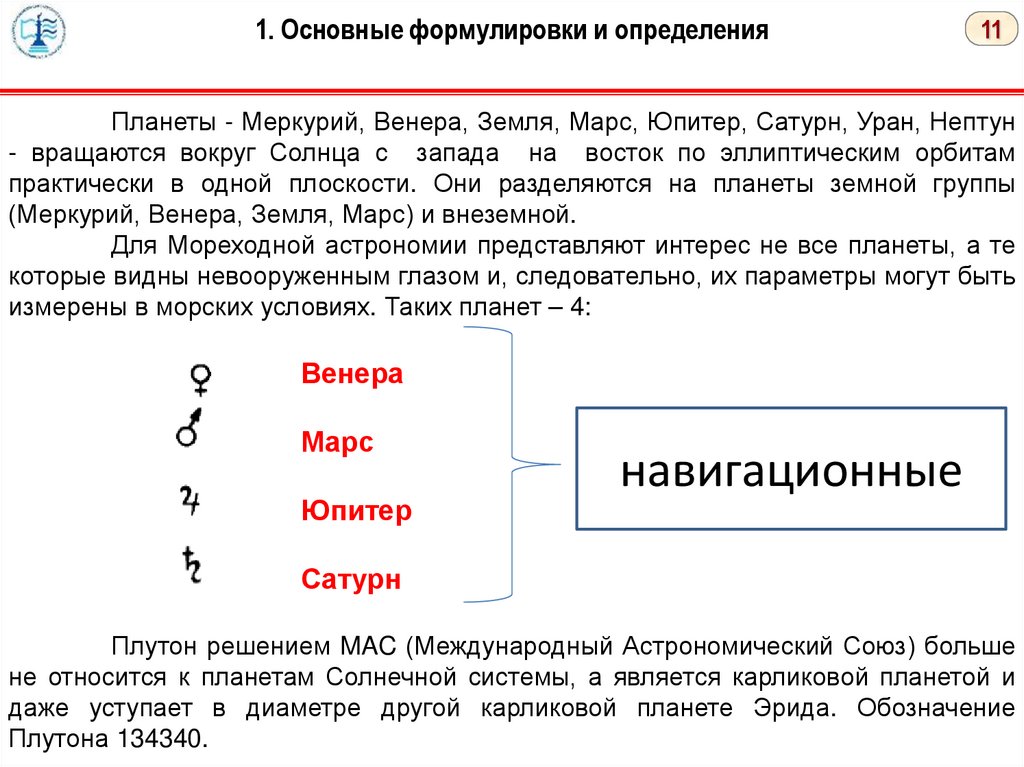
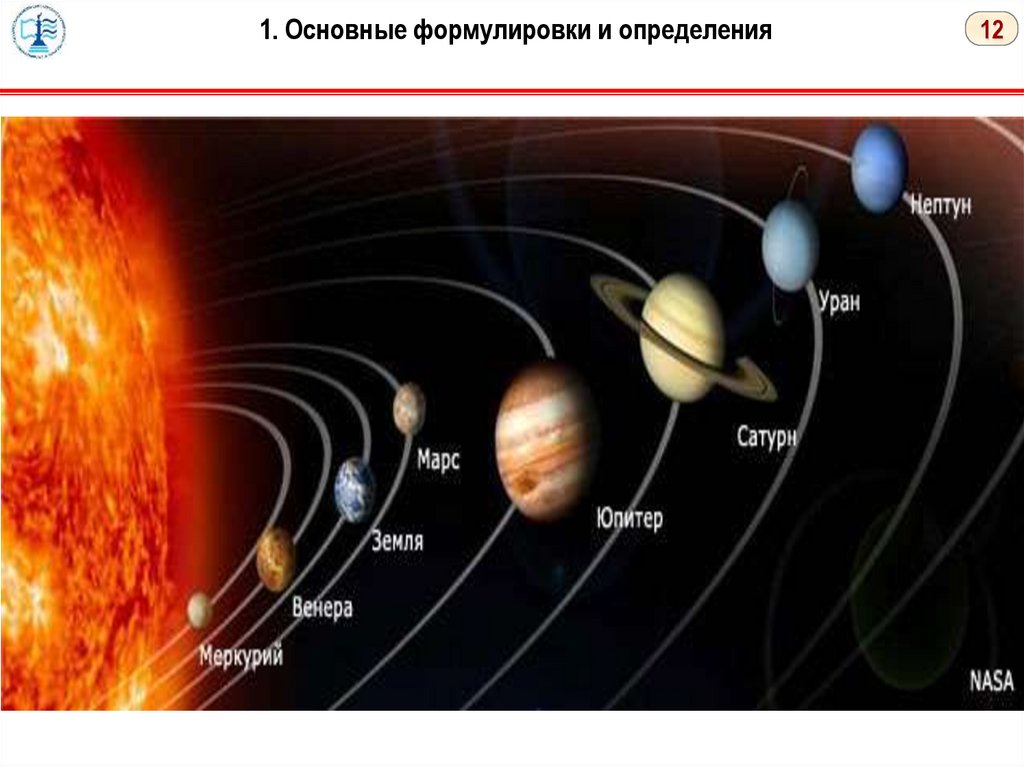
Планеты - Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун
- вращаются вокруг Солнца с запада на восток по эллиптическим орбитам
практически в одной плоскости. Они разделяются на планеты земной группы
(Меркурий, Венера, Земля, Марс) и внеземной.
Для Мореходной астрономии представляют интерес не все планеты, а те
которые видны невооруженным глазом и, следовательно, их параметры могут быть
измерены в морских условиях. Таких планет – 4:
Венера
Марс
Юпитер
навигационные
Сатурн
Плутон решением MAC (Международный Астрономический Союз) больше
не относится к планетам Солнечной системы, а является карликовой планетой и
даже уступает в диаметре другой карликовой планете Эрида. Обозначение
Плутона 134340.

12.

1. Основные формулировки и определения
12

13.

1. Основные формулировки и определения
Движение светил легче всего представить и изобразить на вспомогательной
сферической поверхности, которая в астрономии называется небесной сферой.
Вспомогательная небесная сфера (ВНС) - это сфера произвольного
радиуса с центром в произвольной точке, на поверхность которой проецируются
изображения звезд, образуя при этом их видимые места. За произвольную точку
обычно принимается центр Земли (вследствие больших расстояний до светил
размерами Земли можно пренебречь).
13

14.

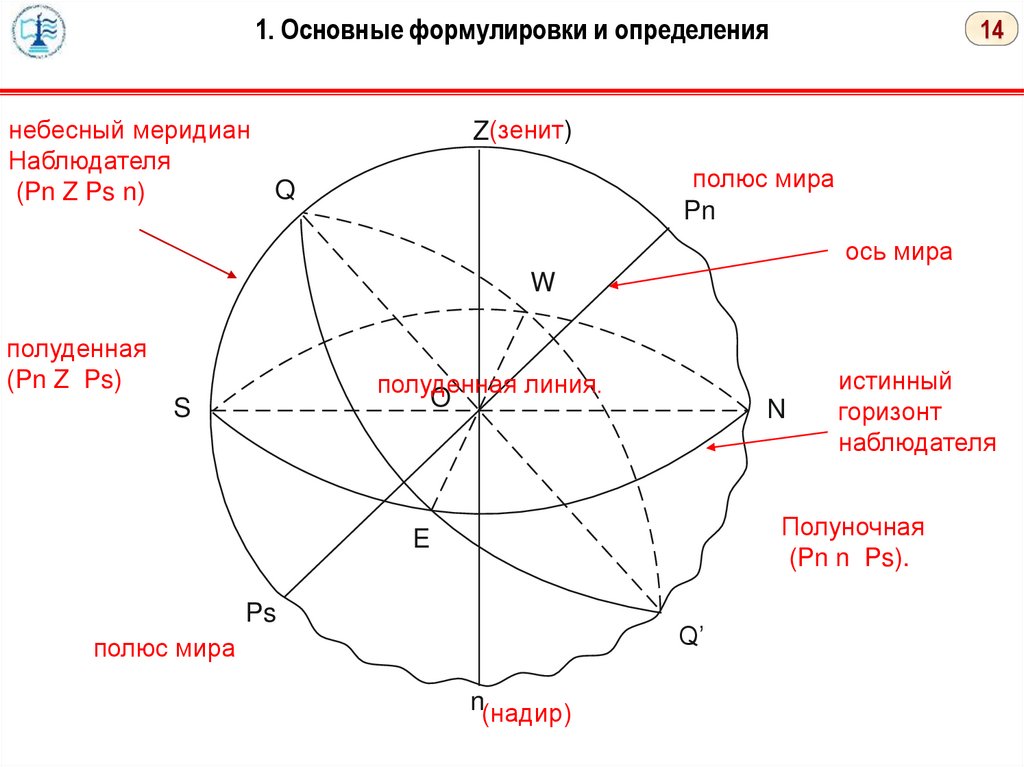
1. Основные формулировки и определения
небесный меридиан
Наблюдателя
Q
(Pn Z Ps n)
14
Z(зенит)
полюс мира
Pn
ось мира
W
полуденная
(Pn Z Ps)
полуденная линия.
O
S
N
истинный
горизонт
наблюдателя
Полуночная
(Pn n Ps).
E
Ps
Q’
полюс мира
n(надир)

15.

1. Основные формулировки и определения
15
1. Пересечение земной оси с небесной сферой дает точки Pn и Ps - полюса мира. Pn повышенный полюс мира, Ps - пониженный полюс мира. Линия PnPs - ось мира.
2. Пересечение отвесной линии с небесной сферой образует точки Z (зенит) и n (надир).
3. Пересечение плоскости меридиана наблюдателя с небесной сферой образует большой
круг - небесный меридиан наблюдателя (Pn Z Ps n). Небесный меридиан наблюдателя
осью мира делится на 2 части - полуденную (Pn Z Ps) и полуночную (Pn n Ps).
4. Пересечение плоскости истинного горизонта с небесной сферой образует большой круг
- истинный горизонт наблюдателя. Пересечение небесного меридиана наблюдателя с
истинным горизонтом дает точки N и S. Линия NS - полуденная линия.
5. Пересечение плоскости земного экватора с поверхностью сферы образует большой круг
- небесный экватор. Пересечение небесного экватора и плоскости истинного горизонта
дает точки E и W.
Небесная сфера делится плоскостями на части:
- меридианом наблюдателя Pn Z Ps n - на восточную и западную;
- истинным горизонтом - на подгоризонтную и надгоризонтную;
- небесным экватором - на северную (Pn) и южную (Ps) части.
Положение точки на сферической поверхности определяется пересечением двух кругов.

16.

1. Основные формулировки и определения
16

17.

1. Основные формулировки и определения
17
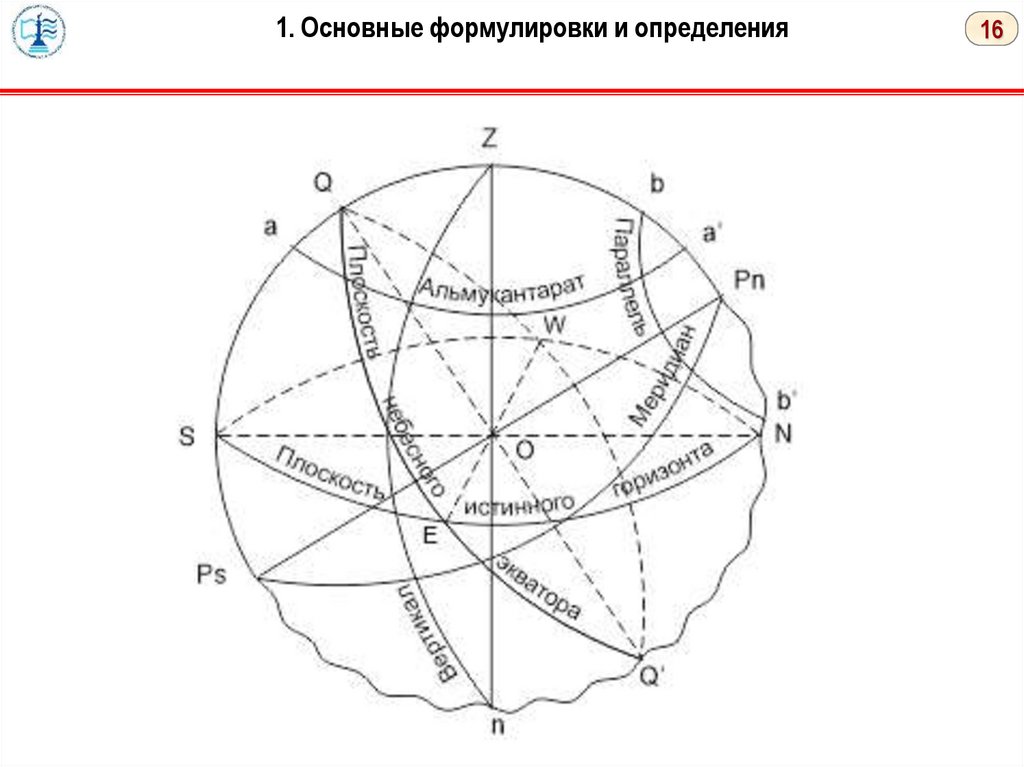
Большие круги, плоскости которых проходят через отвесную линию (Zn),
называются вертикалами.
Они перпендикулярны плоскости истинного горизонта.
Вертикал, проходящий через точки Е и W, называется первым.
Малые круги, параллельные плоскости истинного горизонта, называются
альмукантаратами.
Большие круги, плоскости которых проходят через ось мира (PnPs), называются
небесными меридианами. Они перпендикулярны плоскости небесного экватора.
Малые круги, перпендикулярные оси мира, называются небесными
параллелями.

18.

2. Системы координат
18
В мореходной астрономии известны 5 систем координат, но мы будем
использовать 3 системы сферических координат, представляющих собой
совокупность координатных плоскостей, координатных линий и
непосредственно самих координат:
- горизонтная - счет ведется от истинного горизонта и меридиана
наблюдателя;
- 1-я экваториальная - счет ведется от небесного экватора и меридиана
наблюдателя;
- 2-я экваториальная - счет ведется от небесного экватора и точки Овна.

19.

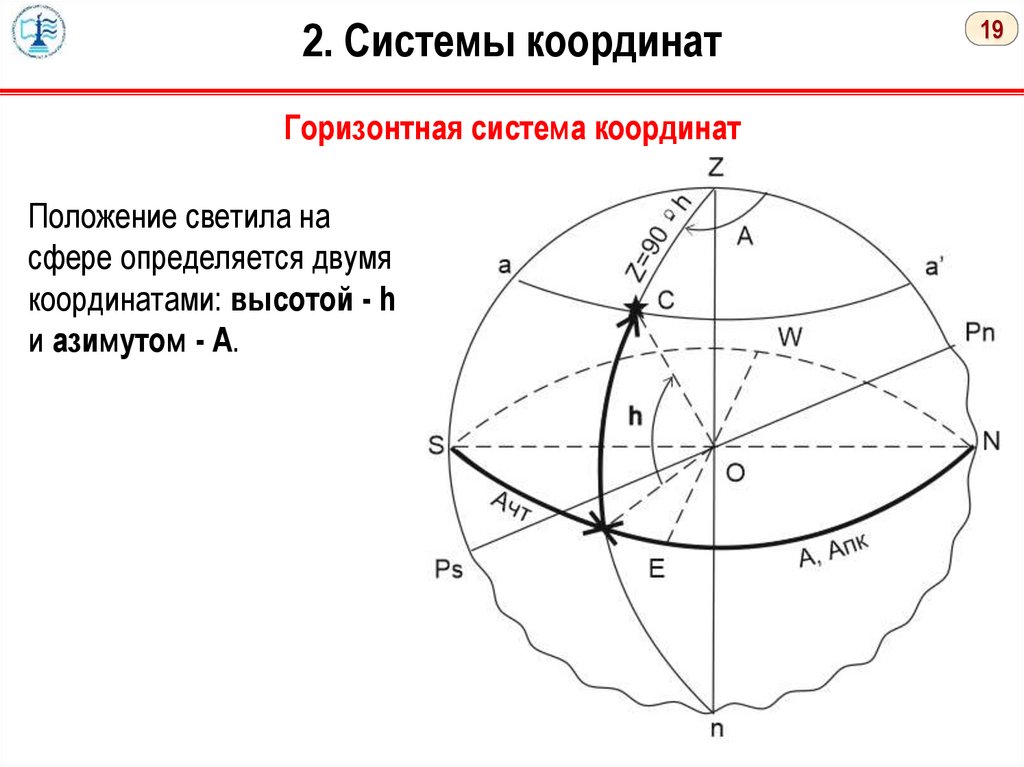
2. Системы координат
Горизонтная система координат
Положение светила на
сфере определяется двумя
координатами: высотой - h
и азимутом - А.
19

20.

2. Системы координат
20
Высота светила (h) - вертикальный угол при центре сферы между
плоскостью истинного горизонта и направлением на светило, измеряемый
дугой вертикала светила от истинного горизонта до альмукантарата
светила в пределах от 0° до 90°.
Дополнение высоты до 90° называется зенитным расстоянием
(0º -180º)
Z = 90° - h.
Азимут светила (А) - сферический угол при зените, заключенный
между меридианом наблюдателя и вертикалом светила.

21.

2. Системы координат
21
В зависимости от начала отсчета, направления и пределов измерения
применяются 3 способа измерения азимутов.
Азимут в круговом счете (Ак) измеряется дугой истинного горизонта
всегда от точки N в сторону Е до вертикала светила в пределах от 0° до 360°.
Записывается Ак = 120°.
В полукруговом счете (Ап) азимут измеряется дугой истинного
горизонта от полуночной части меридиана наблюдателя до вертикала светила в
сторону Е или W в пределах от 0° до 180°. Записывается АП = N120°Е.
Азимут в четвертном счете (Ачт) измеряется дугой истинного горизонта
от ближайшей части меридиана наблюдателя до вертикала светила в сторону Е
или W в пределах от 0° до 90°. Записывается Ачт = SE60°=60°SE.
Горизонтные координаты светил определяются путем наблюдений с
помощью секстана - высота светила (h) и компаса - азимут светила (А). Однако
вследствие вращения Земли и перемещения наблюдателя по поверхности Земли
высоты и азимуты светил постоянно изменяют свои значения.

22.

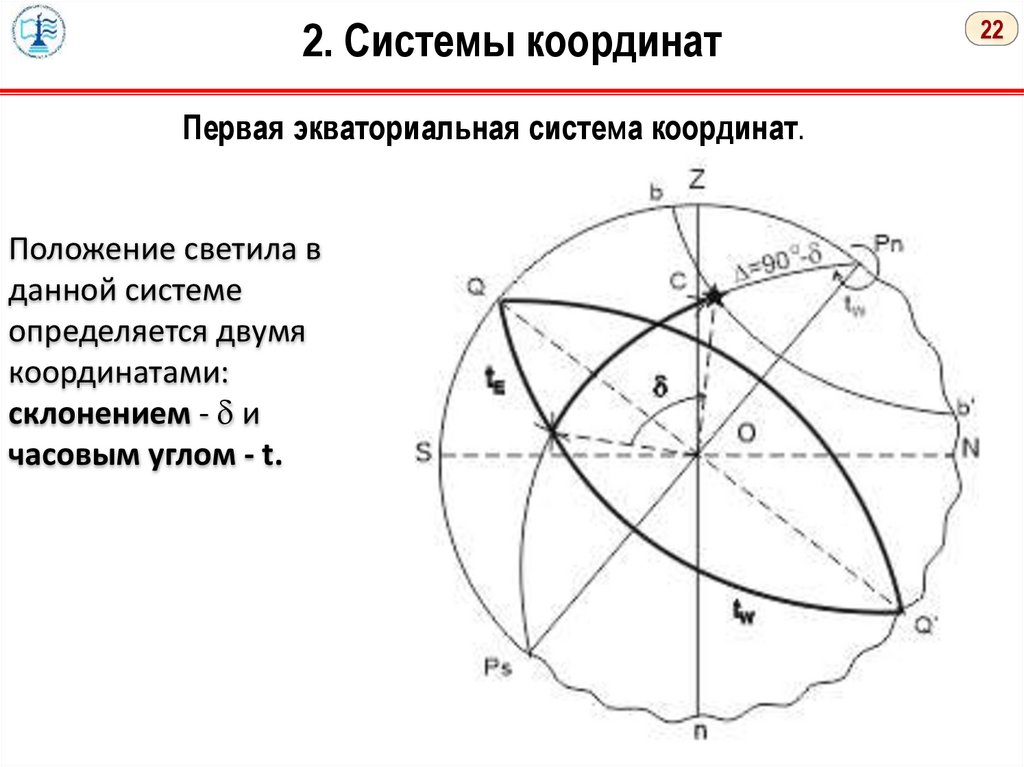
2. Системы координат
Первая экваториальная система координат.
Положение светила в
данной системе
определяется двумя
координатами:
склонением - и
часовым углом - t.
22

23.

2. Системы координат
23
Склонение светила (δ) - угол при центре небесной сферы между
плоскостью небесного экватора и направлением на светило, измеряемый дугой
небесного меридиана светила от небесного экватора до параллели светила в
пределах от 0° до 90° и имеющий наименование того полушария, в котором
находится данное светило (N или S). Измеряется в обсерваториях.
Часовой угол (t) - сферический угол при повышенном полюсе мира
между полуденной частью меридиана наблюдателя и меридианом светила
измеряется дугой небесного экватора от точки Q до меридиана светила в сторону
W в пределах от 0º до 360º. Такой часовой угол называется вестовым или
обыкновенным. При решении задач сферической тригонометрии оперируют с
углами, не превышающими величину 180º. Такие часовые углы называются
практическими. Если tW > 180º, то его следует перевести в практический счет
tE = 360º - tW .
Полярное расстояние (Δ) - дуга меридиана светила от повышенного
полюса до параллели светила Δ = 90º - δ .

24.

2. Системы координат
Вторая экваториальная система координат
Отличие 2-й экваториальной системы сферических координат
от 1-й заключается в том, что часовой угол (t), изменяющийся во
времени, заменен на иную координату - прямое восхождение (α), не
связанную со временем и местом наблюдения.
24

25.

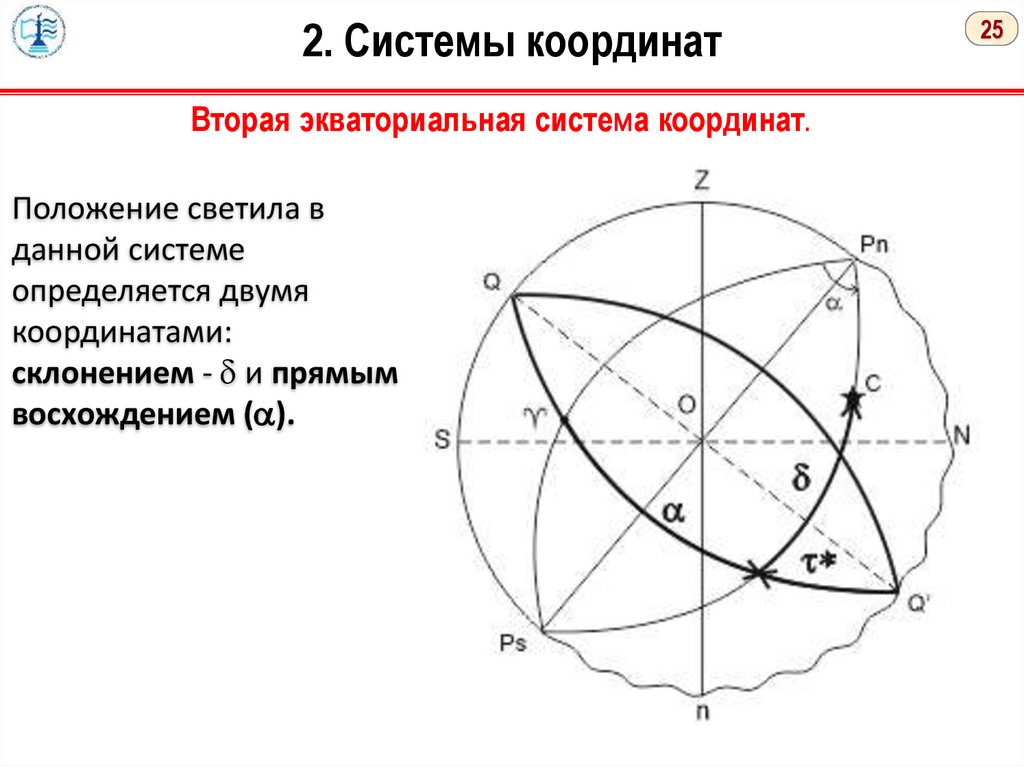
2. Системы координат
Вторая экваториальная система координат.
Положение светила в
данной системе
определяется двумя
координатами:
склонением - и прямым
восхождением ( ).
25

26.

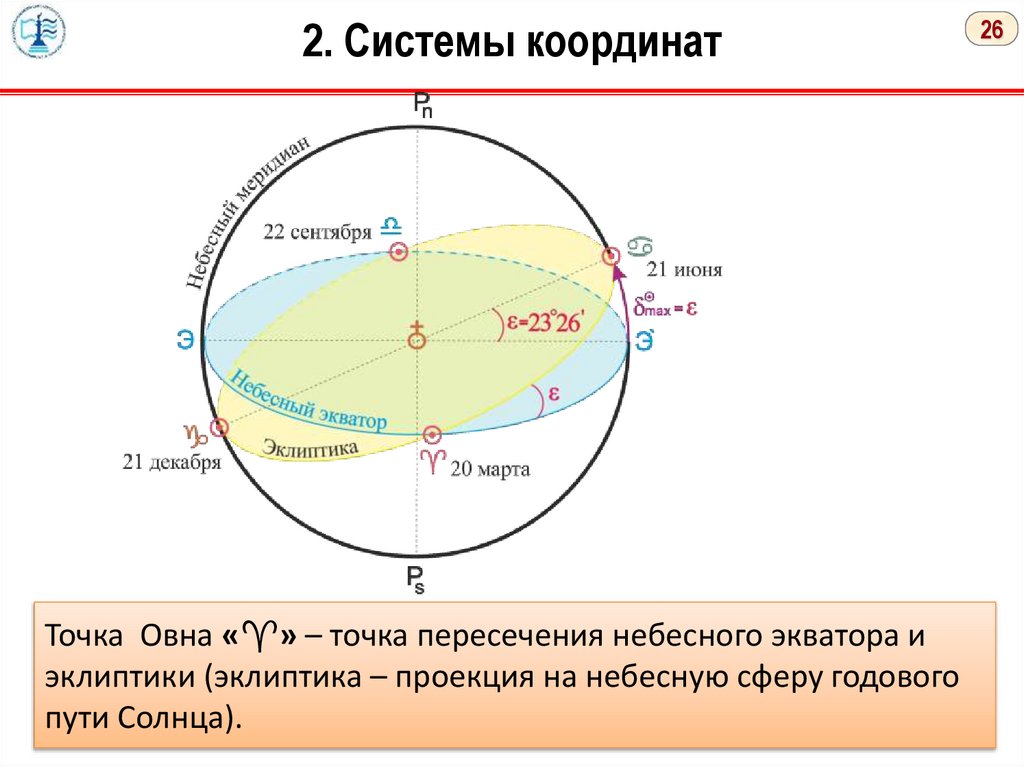
2. Системы координат
Точка Овна « » – точка пересечения небесного экватора и
эклиптики (эклиптика – проекция на небесную сферу годового
пути Солнца).
26

27.

2. Системы координат
27

28.

2. Системы координат
28

29.

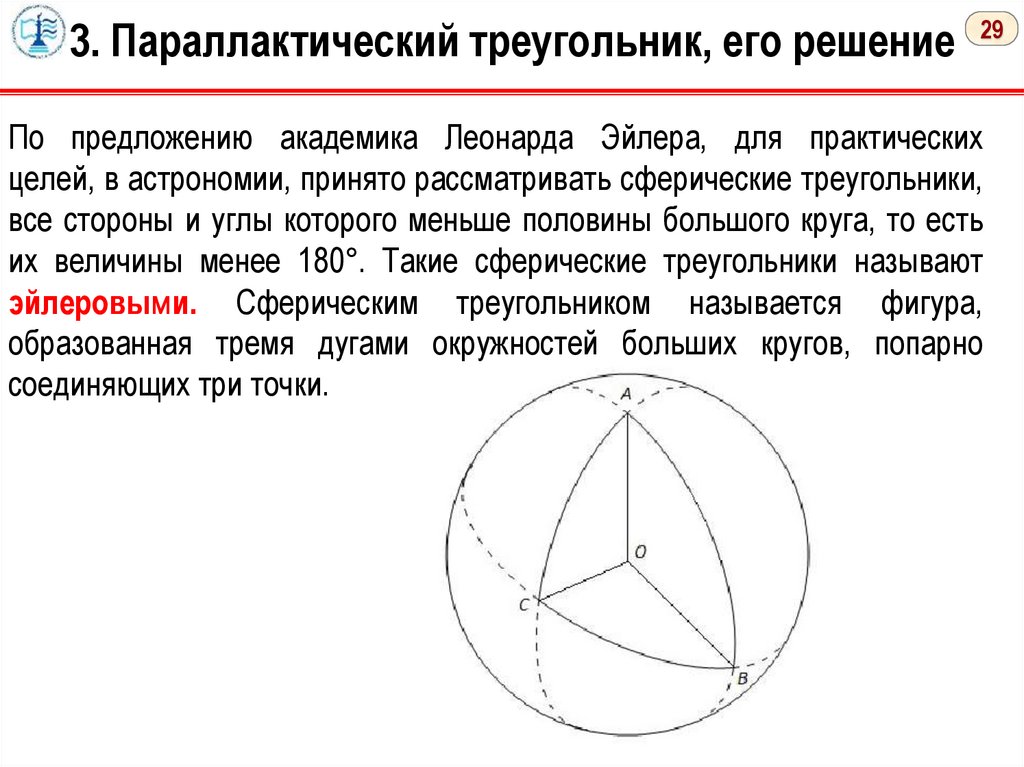
3. Параллактический треугольник, его решение 29
По предложению академика Леонарда Эйлера, для практических
целей, в астрономии, принято рассматривать сферические треугольники,
все стороны и углы которого меньше половины большого круга, то есть
их величины менее 180°. Такие сферические треугольники называют
эйлеровыми. Сферическим треугольником называется фигура,
образованная тремя дугами окружностей больших кругов, попарно
соединяющих три точки.

30.

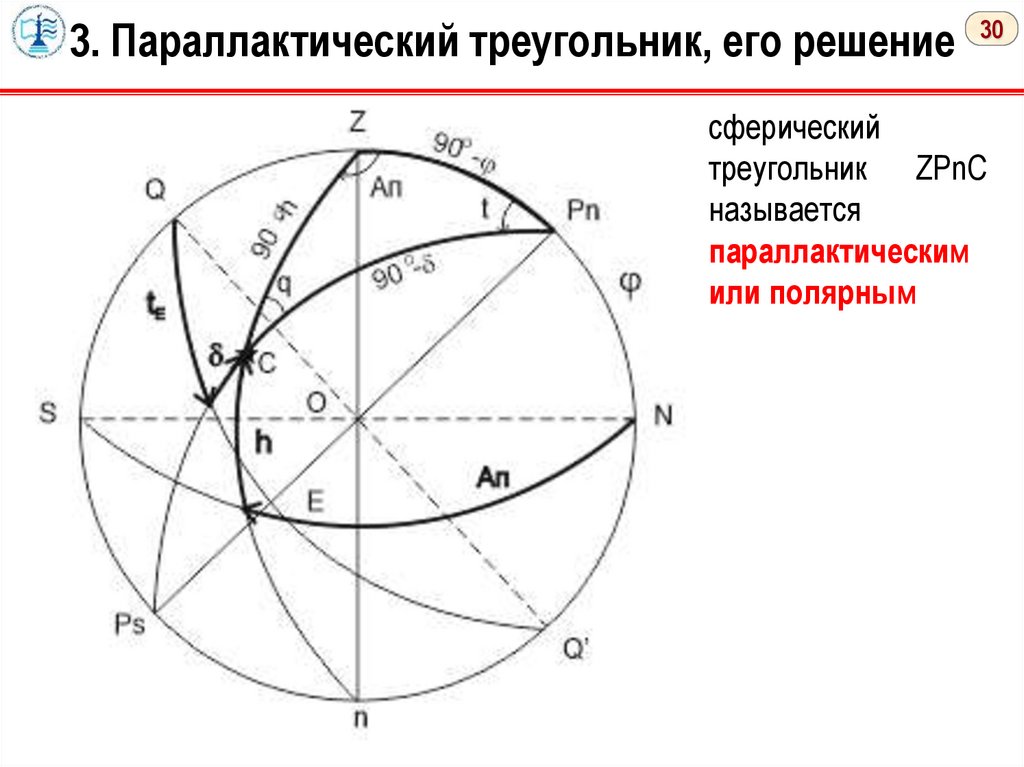
3. Параллактический треугольник, его решение 30
сферический
треугольник ZPnC
называется
параллактическим
или полярным

31.

3. Параллактический треугольник, его решение 31
В
сферической
тригонометрии
рассмотрение
сферического
треугольника сводится к его решению.
Решение заключается в том, чтобы, используя три известных элемента,
получить неизвестные элементы.
Для решения пользуются основными формулами сферической
тригонометрии, выведенными для решения сферических треугольников, углы и
стороны которых менее 180°. К ним относятся:
формула синусов:
формула косинусов:
формула для четырёх
подряд лежащих элементов :
формула пяти элементов:
cos a = cos b cos c + sin b sin c cos A
ctg B sin A = ctg c sin b - cos c cos A
sin a cos B = cos b sin c - sin b cos c cos A

32.

3. Параллактический треугольник, его решение 32
Элементами параллактического треугольника являются:
- угол при зените - азимут полукругового счета Ап;
- угол при полюсе - часовой угол светила (t);
- угол при светиле - параллактический угол (q);
- сторона Z Pn - дополнение широты до 90°, т. е. 90° - ϕ;
- сторона Pn C - дополнение склонения до 90° - полярное расстояние
Δ = 90° - δ;
- сторона Z C - дополнение высоты до 90° - зенитное расстояние
Z = 90° - h.
Параллактический треугольник связывает небесные координаты горизонтные и экваториальные с географическими координатами
наблюдателя.

33.

3. Параллактический треугольник, его решение 33

34.

3. Параллактический треугольник, его решение 34

35.

3. Параллактический треугольник, его решение 35

36.

3. Параллактический треугольник, его решение 36
Исследование на знаки обязательно, при этом следует помнить:
- ϕ < 90° и "+";
- δ < 90° и одноименно с ϕ, то "+", если разноименно "-". Если склонение
одноимённо с ϕ, то все функции имеют " + ", если же склонение разноимённо с ϕ, то
сosδ и secδ имеют знак " + ", остальные "-".
- h < 90°, но может иметь «+» или «-», если «+», то и все «+», если «-», cos h и
sec h " + ", , остальные функции "-";
- t < 180° (Е или W), если tм < 90° , то все " + ", а если tм > 90°, то sin t и cosec
t имеют знак " + ", а остальные функции знак " - ";
- A < 180°, при этом: если А < 90° - все функции азимута имеют знак " + ", если
А > 90°, то sin А и cosec А имеют знак " + ", остальные " -";
- параллактический угол может принимать значения от 0° до 180°, знаки как у
азимутов и часовых углов.

37.

3. Параллактический треугольник, его решение 37
Правила определения наименования азимутов
Наименование δ
Величина δ
Величина hc
Разноименно с
широтой
Одноимённо с
широтой
1-я буква Ас
2-я буква Ас
Разноименно с
широтой
δ<φ
hc > h 1
Разноименно с
широтой
δ<φ
hc < h 1
Одноименно с
широтой
δ>φ
Не имеет
значение
Одноименно с
широтой
Всегда одного
наименования с
часовым углом

38.

3. Параллактический треугольник, его решение 38
Таблицы для вычисления высоты и азимута были
разработаны проф. Ющенко А.П. и впервые были
опубликованы в Мореходных таблицах изд. 1943
г., а затем отдельным изданием в 1952 и 1957 г.г.
В основу вычислений высот и азимутов светил по
ТВА – 57 положено решение параллактического
треугольника методом перехода к двум
прямоугольным сферическим треугольникам.
Ющенко Артемий Павлович - (1895—1968 г.)
доктор технических наук, профессор, гидрограф-геодезист, доктор
военно-морских наук, заслуженный деятель наук, капитан 1 ранга,
почетный полярник. Штурман, гидрограф, физик, геодезист

39.

3. Параллактический треугольник, его решение 39

40.

3. Параллактический треугольник, его решение 40

41.

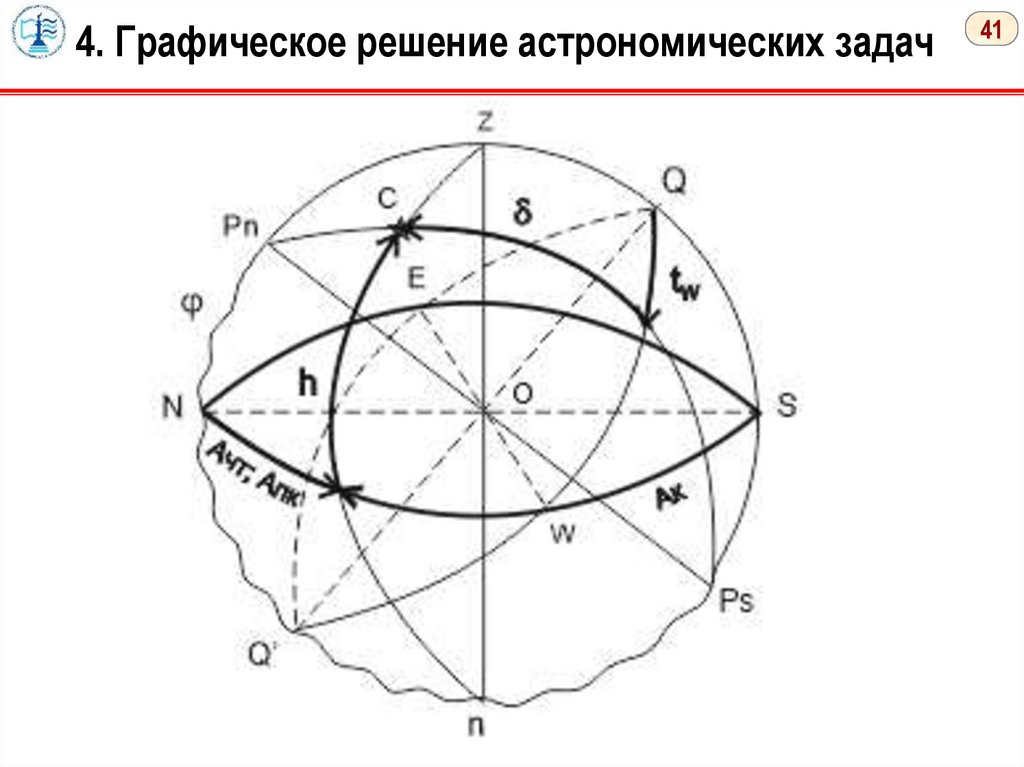
4. Графическое решение астрономических задач
41