Похожие презентации:
теорема Фалеса
1. составьте алгоритм, как разделить отрезок, равный 7 см 1 вариант: на две равные части, 2 вариант: на четыре равные части, 3
вариант: на три равные части2.
Считается, что именно он «привез» геометрию из Египта ипознакомил с ней греков. Его деятельность привлекла
последователей и учеников, которые образовали милетскую
школу. Считается, что с милетской школы начинается история
европейской науки.
3.
Легенда рассказывает отом, что он, будучи в
Египте, поразил фараона
Амасиса тем, что сумел
точно установить высоту
пирамиды, дождавшись
момента, когда длина
тени палки становится
равной её высоте, и
тогда измерил длину
тени пирамиды.
4.
• Есть одна точная дата, связанная с егожизнью, — 585 до н. э., когда в Милете было
солнечное затмение, которое он предсказал.
5. Но одна из важнейших заслуг его в том, что ему приписываются многие геометрические теоремы
• круг делится диаметром пополам;• в равнобедренном треугольнике углы при
основании равны;
• при пересечении двух прямых образуемые
ими вертикальные углы равны;
• два треугольника равны, если два угла и
сторона одного из них равны двум углам и
соответствующей стороне другого.
6.
Фалес МилетскийДревнегреческий ученый
(ок. 625 – 547 гг. до н. э.)
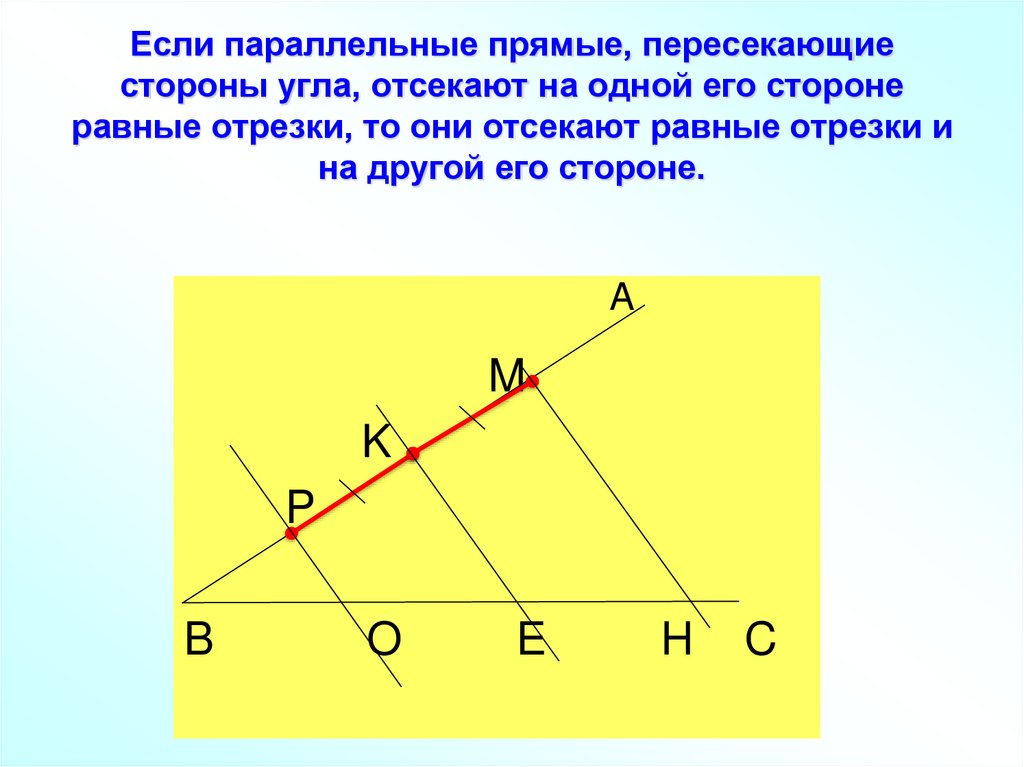
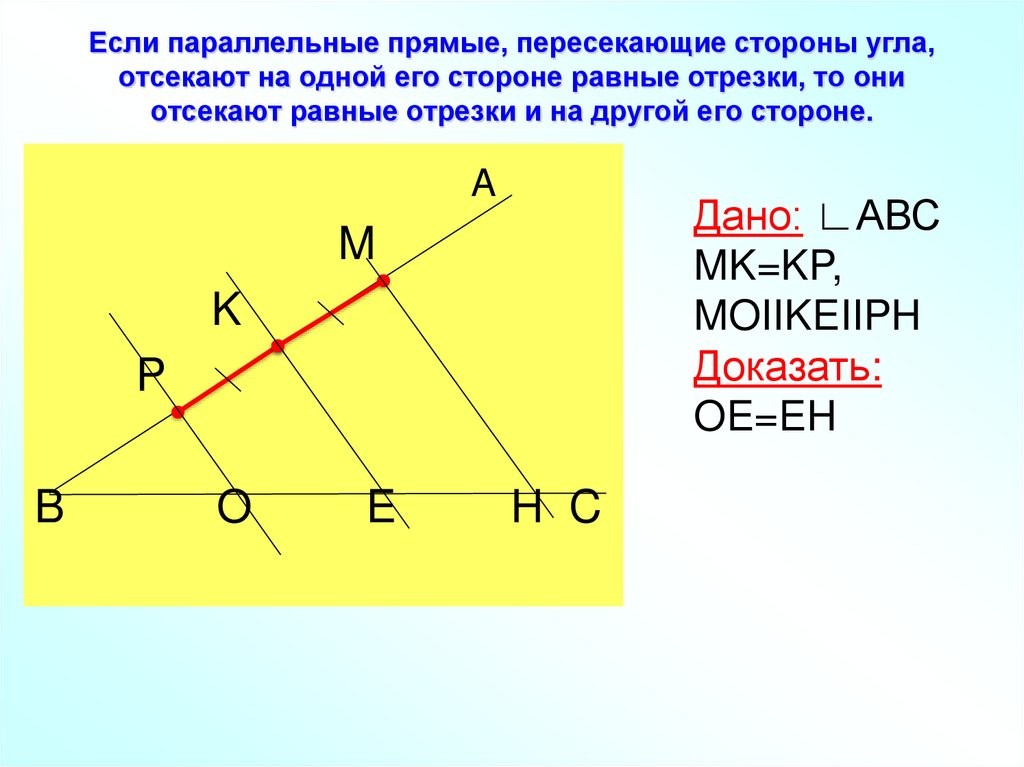
Если параллельные прямые, пересекающие стороны угла,
отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.
7. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные
отрезки ина другой его стороне.
A
M
K
P
B
O
E
H
C
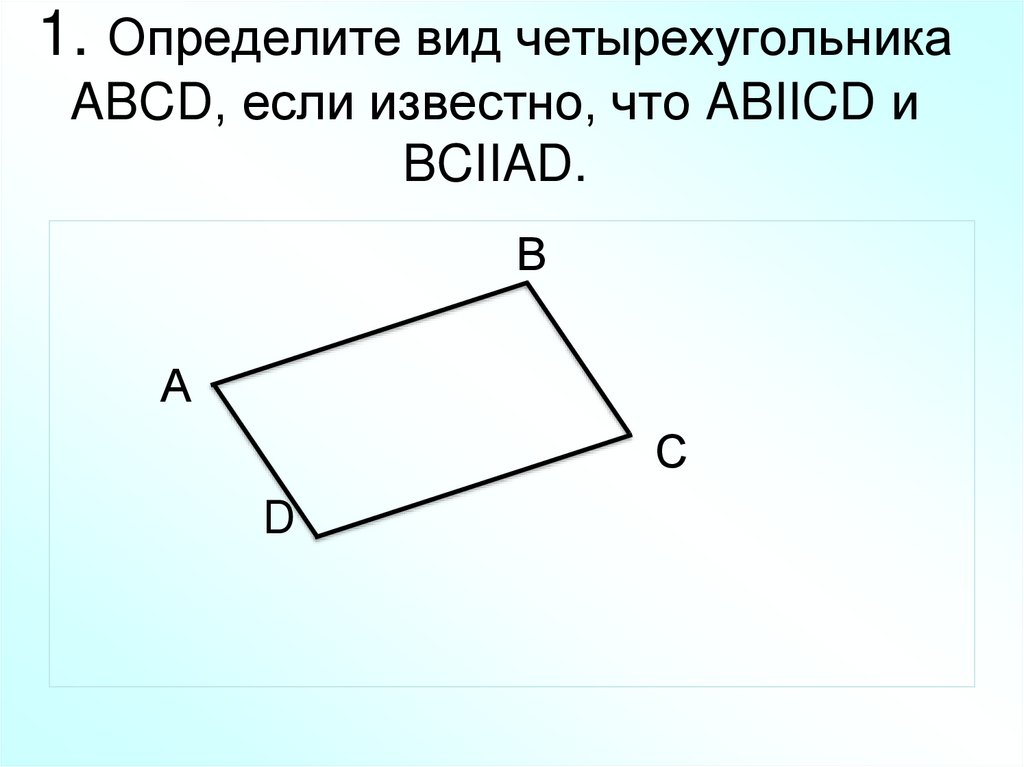
8. 1. Определите вид четырехугольника ABCD, если известно, что ABIICD и BCIIAD.
ВА
С
D
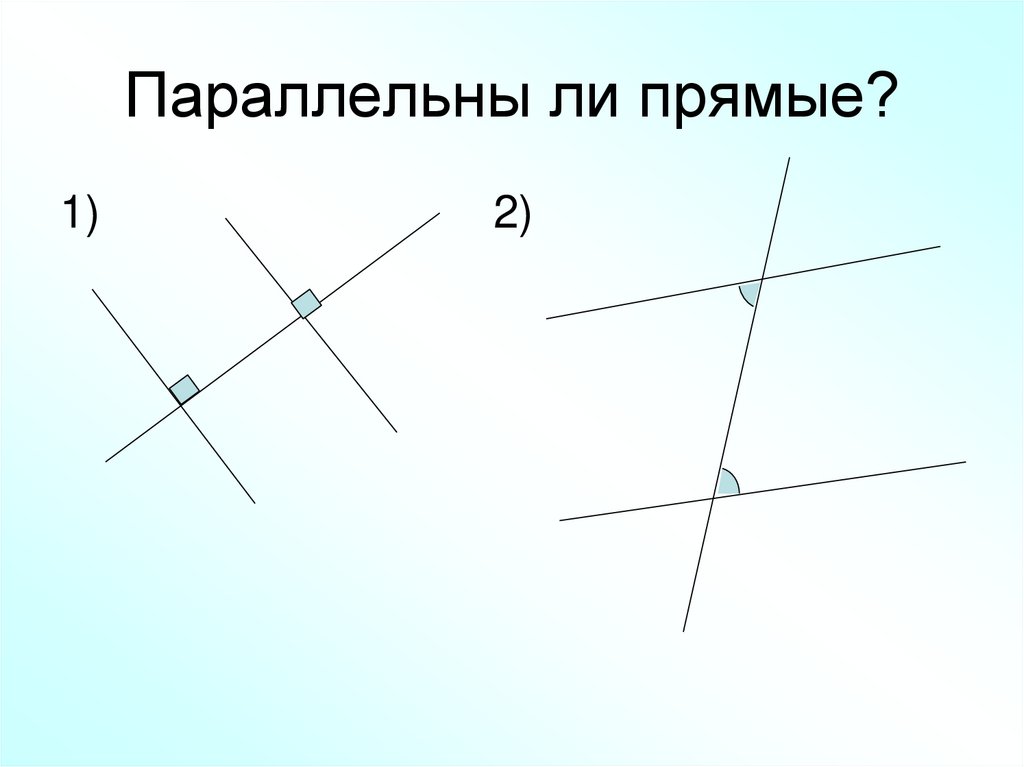
9. Параллельны ли прямые?
1)2)
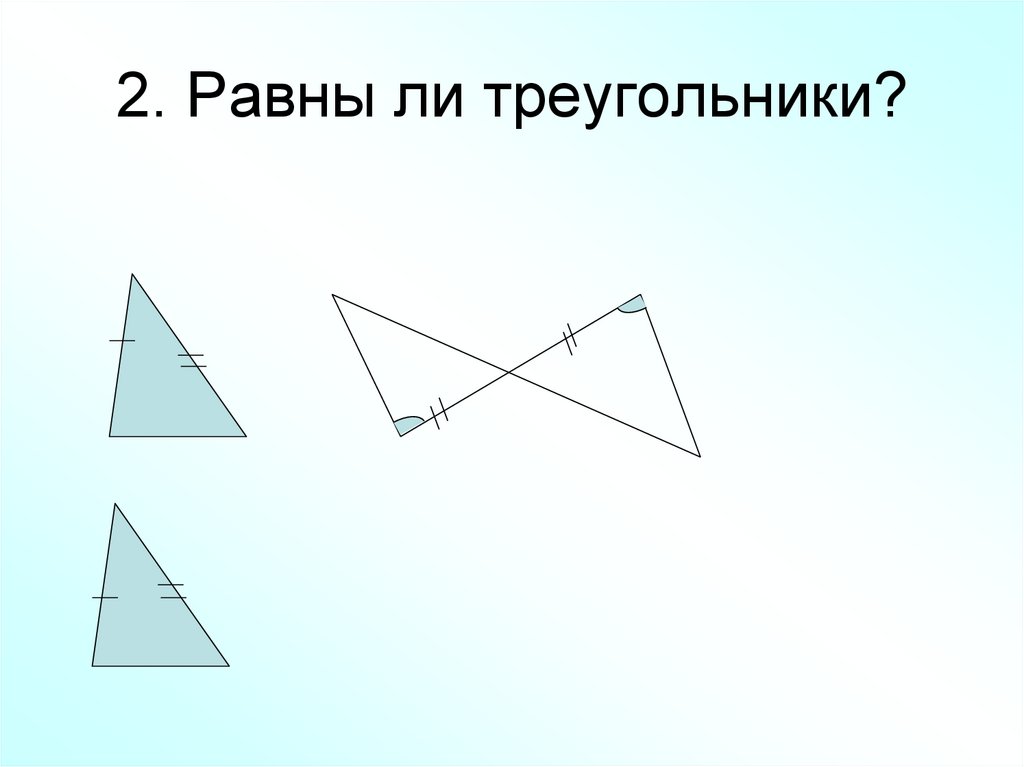
10. 2. Равны ли треугольники?
11. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные
отрезки и на другой его стороне.A
Дано: ∟АВС
MK=KP,
MOIIKEIIPH
Доказать:
OE=EH
M
K
P
B
O
E
H C
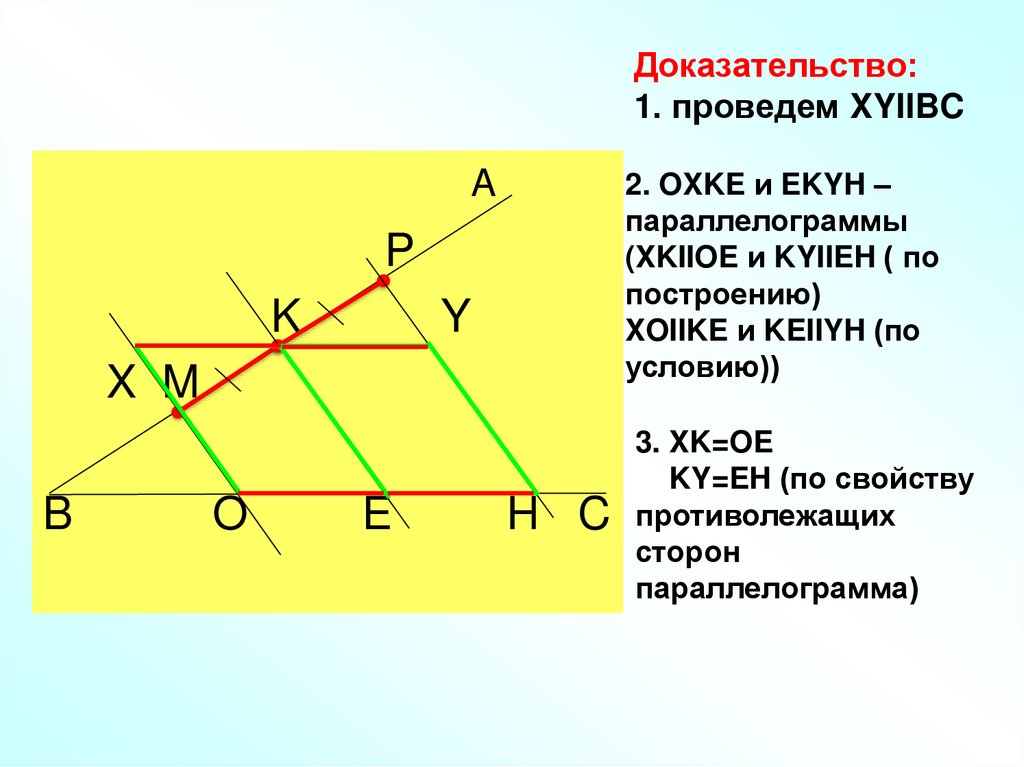
12. Доказательство: 1. проведем XYIIBC
2. OXKE и EKYH –параллелограммы
(XKIIOE и KYIIEH ( по
построению)
XOIIKE и KEIIYH (по
условию))
A
P
K
Y
X M
B
O
E
H C
3. XK=OE
KY=EH (по свойству
противолежащих
сторон
параллелограмма)
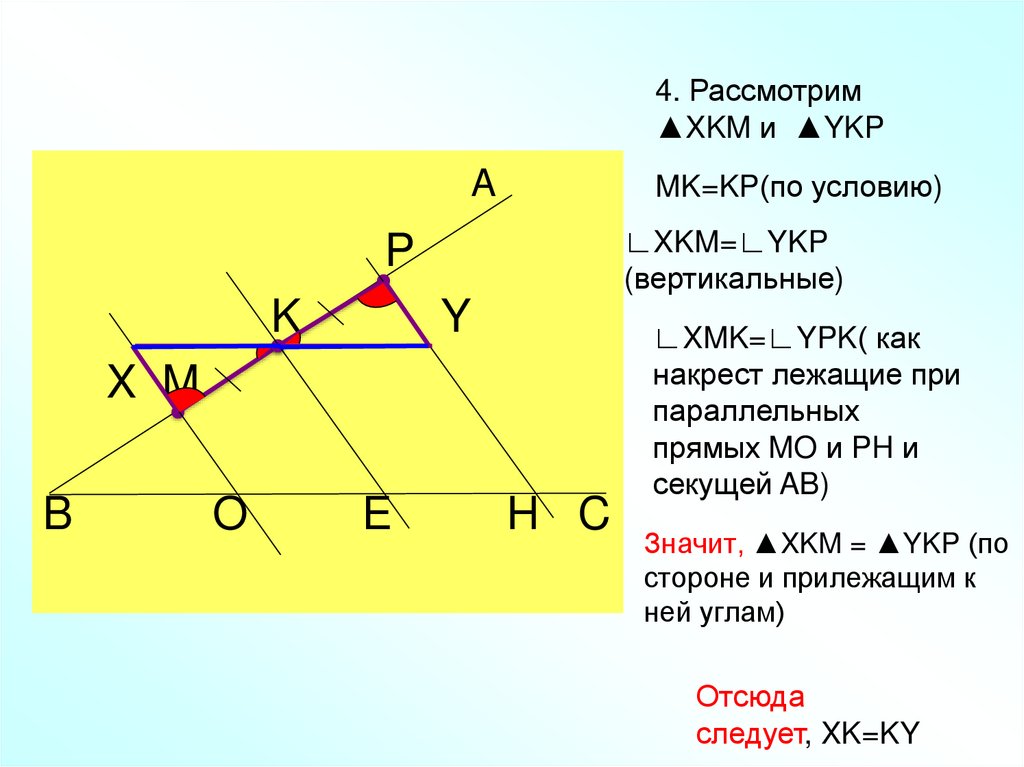
13. Значит, ▲XKM = ▲YKP (по стороне и прилежащим к ней углам)
4. Рассмотрим▲XKM и ▲YKP
A
MK=KP(по условию)
∟XKM=∟YKP
(вертикальные)
P
K
Y
X M
B
O
E
H C
∟XMK=∟YPK( как
накрест лежащие при
параллельных
прямых MO и PH и
секущей AB)
Значит, ▲XKM = ▲YKP (по
стороне и прилежащим к
ней углам)
Отсюда
следует, XK=KY
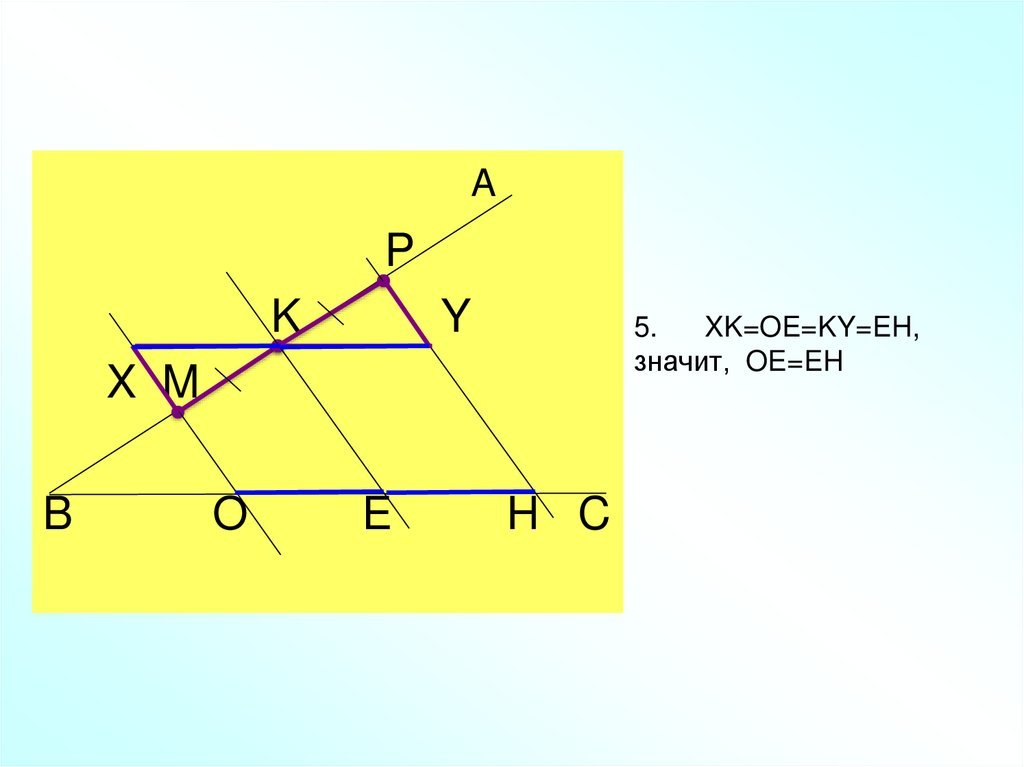
14. 5. XK=OE=KY=EH, значит, OE=EH
AP
K
Y
5.
XK=OE=KY=EH,
значит, OE=EH
X M
B
O
E
H C
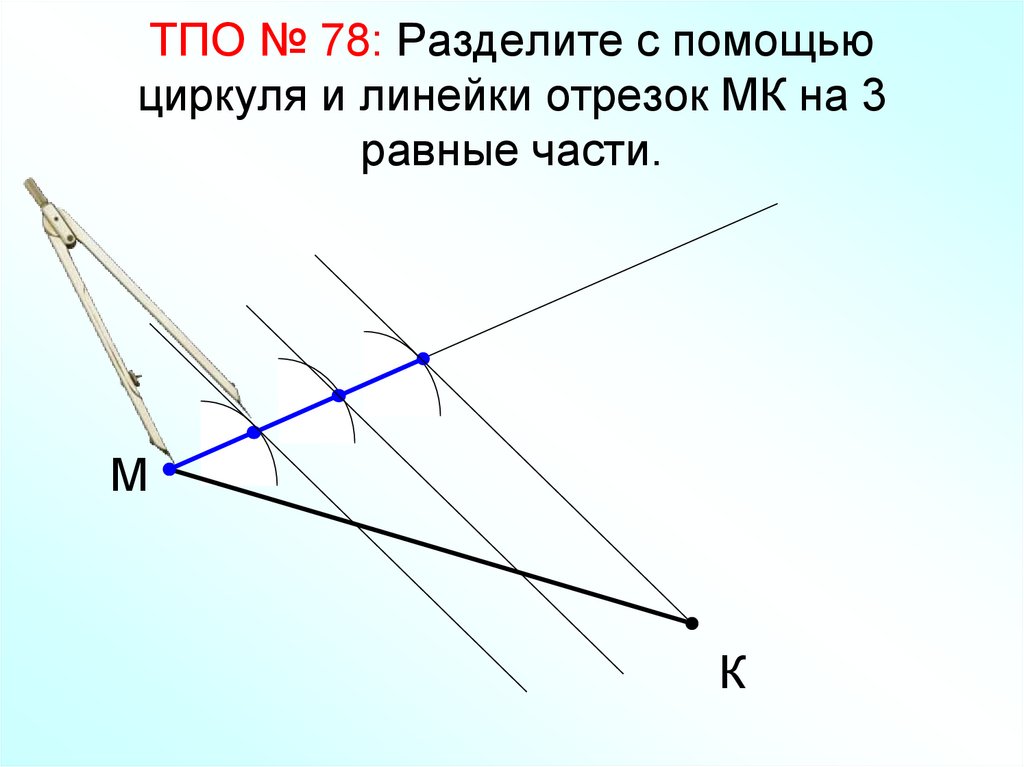
15. ТПО № 78: Разделите с помощью циркуля и линейки отрезок МК на 3 равные части.
МК
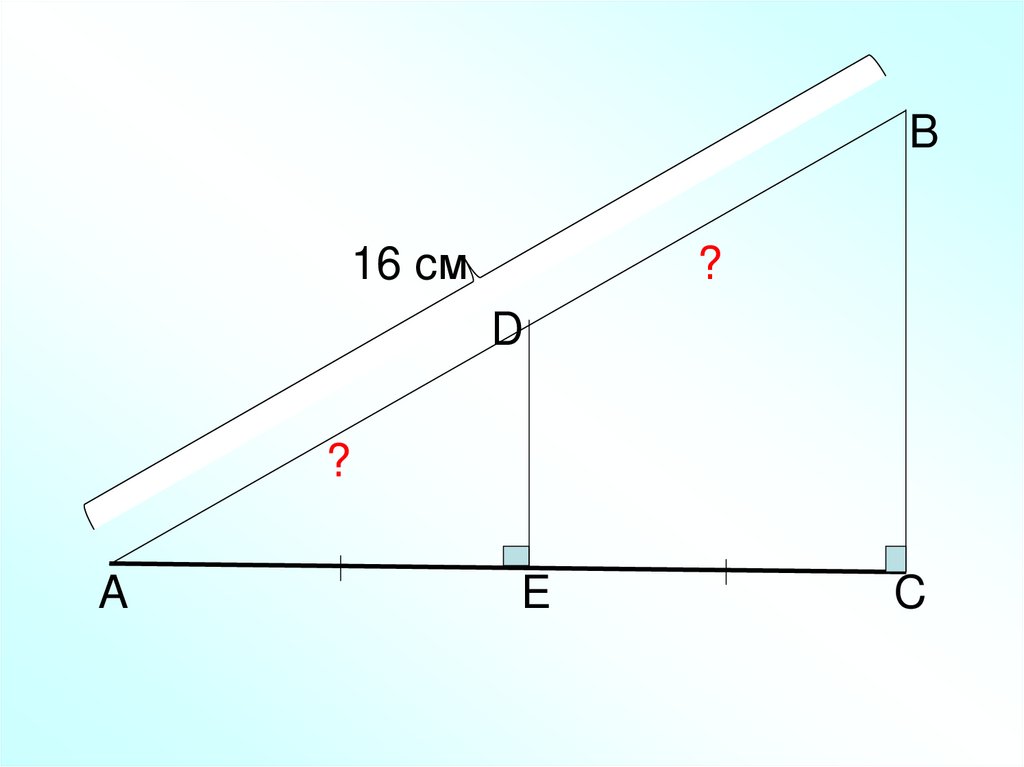
16.
B16 cм
?
D
?
A
E
C
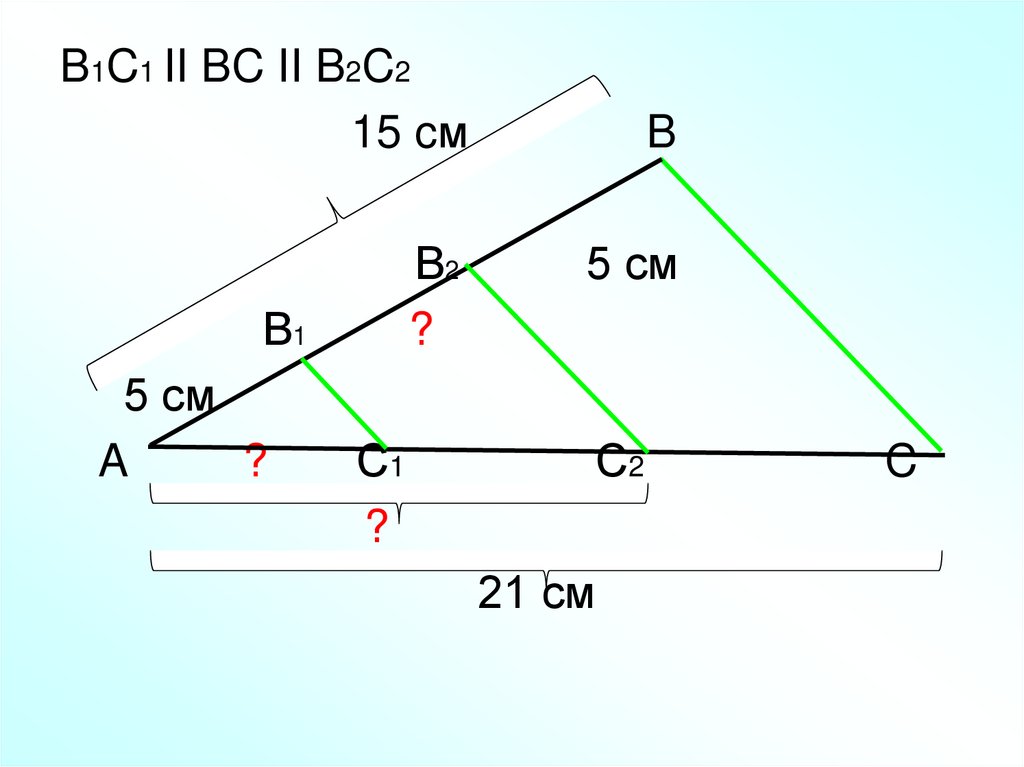
17.
B1C1 II BC II B2C215 cм
В2
?
В1
5 см
A
?
С1
?
B
5 см
С2
21 см
C
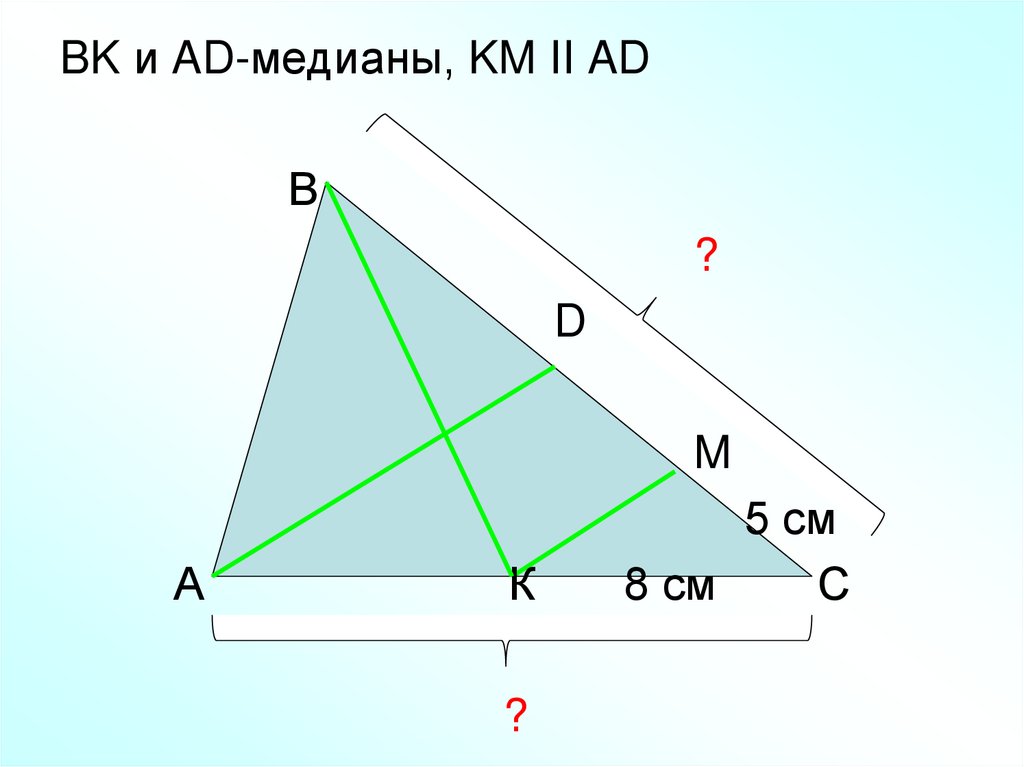
18.
BK и AD-медианы, KM II ADВ
?
D
M
А
К
?
5 см
8 см
С






 Математика
Математика








