Исследование отклика в области эксперимента

1. ИССЛЕДОВАНИЕ ОТКЛИКА В ОБЛАСТИ ЭКСПЕРИМЕНТА

Линейная модель в области экстремума неадекватна.
Поэтому переходят к уравнениям второго порядка.
Чтобы построить полином, содержащий квадраты
факторов. Требуется каждый фактор варьировать на
трех уровнях. Выбор уровней происходит в
зависимости от того какие свойства необходимо
придать плану.
Ортогональное планирование предназначено для
получения ортогонального плана.
Рототабельное планирование обеспечивает
постоянство дисперсий в равноудаленных от центра
плана точках.
1

2. ОРТОГОНАЛЬНОЕ ПЛАНИРОВАНИЕ ВТОРОГО ПОРЯДКА

Полином второго порядка содержит первые и вторые
степени факторов и число коэффициентов:
2
N2 = Ck 2k 1
Для построения таких планов можно применять
трехуровневые планы: N3 = 3к.
Но N3 всегда больше N2 и их разница быстро растет с
ростом к.
Поэтому вместо ПФЭ 3к используют различные
композиционные планы, которые обладают
меньшей избыточностью. За основу (ядро) такого
плана принимается ПФЭ 2к или ДФЭ 2к-р. Ядро
дополняется звездными точками и точкой в центре
плана. Если звездные точки расположены
симметрично относительно центра плана, то это
центрально - композиционный план.
2

3. Планы второго порядка

При k =2 полином содержит 6 членов
^
Y b0 b1 x1 b2 x2 b12 x1 x2 b11 x12 b22 x22
При k = 3 - 11 членов
^
Y b0 b1 x1 b2 x2 b3 x3 b12 x1 x2 b13 x1 x3 b23 x2 x3 b123 x1 x2 x3 b11 x12 b22 x22 b33 x32
Ортогональный центрально-композиционный
план второго порядка (ОЦКП)
N 2k 2k k0 , для ОЦКП k0=1.
Число точек в плане
k
2
3
4
5
6
ОЦКП
9
15
25
43
77
ПФЭ 32
9
27
81
243
729
3

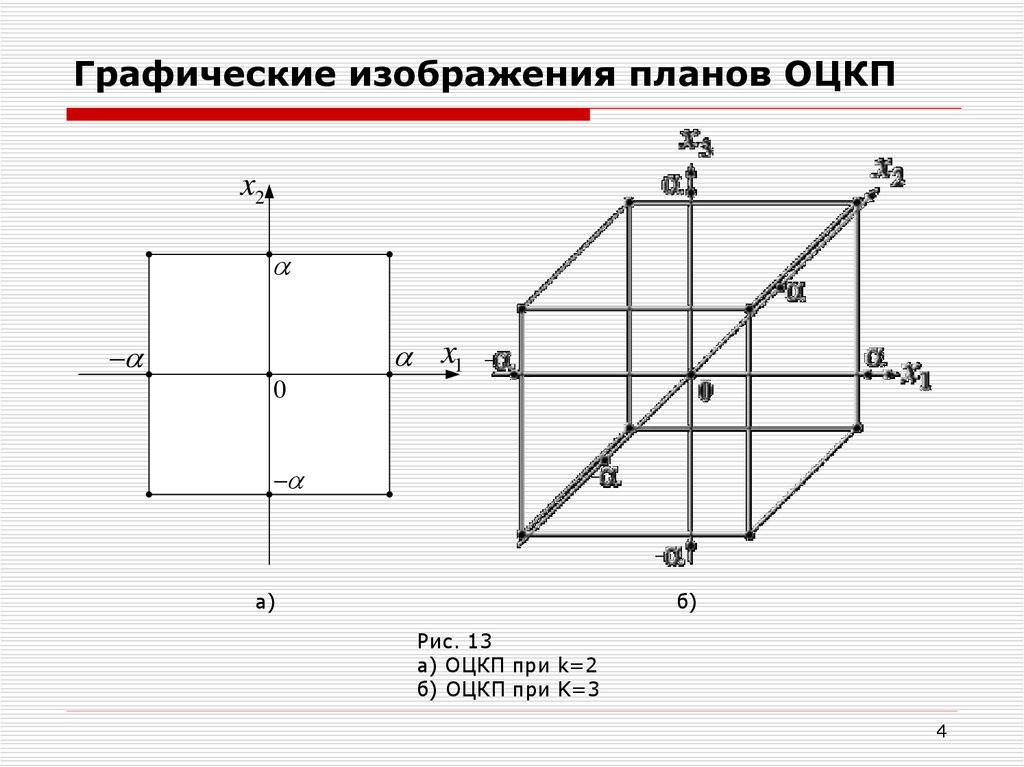
4. Графические изображения планов ОЦКП

x2
x1
0
а)
б)
Рис. 13
а) ОЦКП при k=2
б) ОЦКП при K=3
4

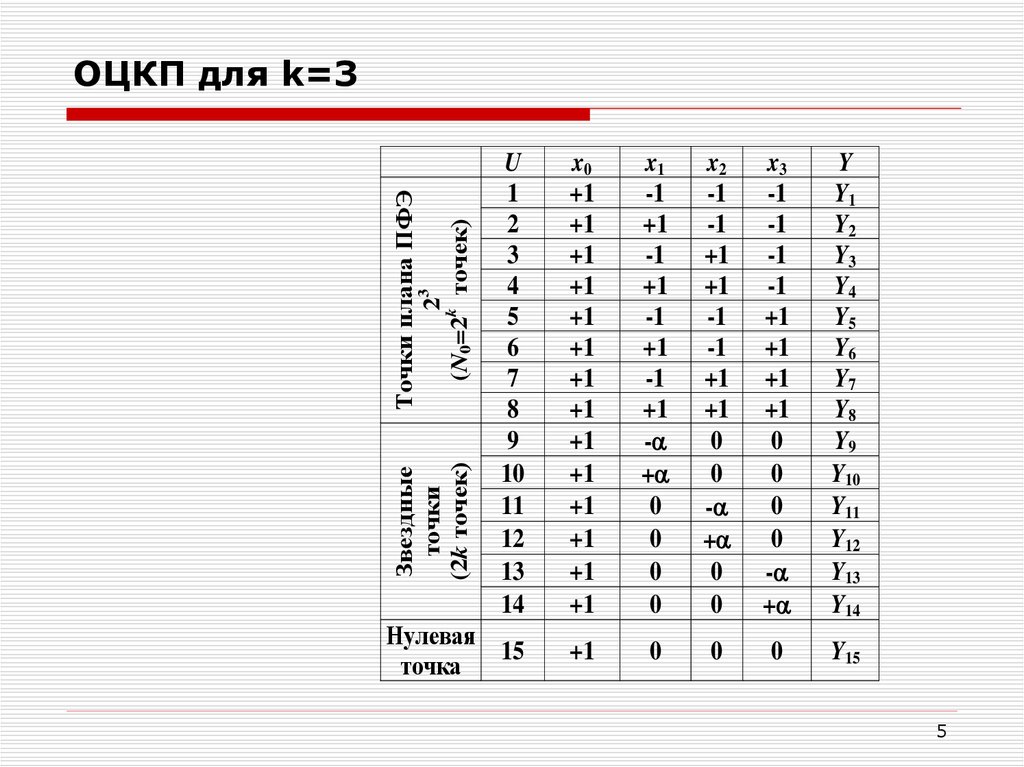
5. ОЦКП для k=3

x0
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
x1
-1
+1
-1
+1
-1
+1
-1
+1
-
+
0
0
0
0
x2
-1
-1
+1
+1
-1
-1
+1
+1
0
0
-
+
0
0
x3
-1
-1
-1
-1
+1
+1
+1
+1
0
0
0
0
-
+
Y
Y1
Y2
Y3
Y4
Y5
Y6
Y7
Y8
Y9
Y10
Y11
Y12
Y13
Y14
Нулевая
15
точка
+1
0
0
0
Y15
Звездные
точки
(2k точек)
Точки плана ПФЭ
23
(N0=2k точек)
U
1
2
3
4
5
6
7
8
9
10
11
12
13
14
5

6. Расчет значений a и a

Расчет значений a и
N0
2k
.
k
N
2 2 k k0
a
1
( N N0 N0 ).
2
Параметры ОЦКП при числе факторов k
k
2
3
4
5
6
1
a
0,667
0,73
0,8
0,86
0,91
N
9
15
25
43
77
7
8
1,215 1,414 1,596 1,761 1,909 2,045
0,946 0,968
143
273
6

7. Расчет коэффициентов

Формулы для расчета коэффициентов уравнения регрессии
ОЦКП, имеют вид
N
N
yu
b0 u 1
N
;
k
a bii
i 1
u 1
n
bi
bij
i j
u 1
2
n
, i=1,2,...,k;
2 2 2
N
xiu yu
N
xiu x ju yu
xiu yu
bii
u 1
(1, a ) 2 2 k 2( 2 a) 2 (k 1)a 2
;
7

8. Расчет дисперсий

Для
ОЦКП
s{bj}
для
четырех
рассчитываются по формулам:
s 2 {bi}
;
s 2 {bii}
2
s âîñ
s {bij}
2
m(2 2 )
k
типов
2
2
s âîñ
коэффициентов
2
s âîñ
m 2
m 2 k (1 a ) 2 2( 2 a) 2 (2k 1)a
k
;
k
s 2 {b0} s 2 {b 0} a 2 s. 2 {bii}
s {b 0}
2
2
sâîñ
i 1
k 2 k 2k 1
8

9. ОТСЕИВАЮЩИЕ ЭКСПЕРИМЕНТЫ

Сложные объекты характеризуются большим числом
количественных и качественных факторов. На
начальном этапе эмпирического изучения таких
объектов трудно сразу спланировать активный
эксперимент, возникают задачи выбора наиболее
важных эффектов и отсеивания несущественных
факторов.
Для решения их применяют методы ранговой
корреляции, случайного баланса и дисперсного
анализа.
9

10. МЕТОД СЛУЧАЙНОГО БАЛАНСА

Метод случайного баланса (МСБ) предназначен для
выделения существенных факторов из множества
переменных и их парных взаимодействий.
МСБ состоит из этапов построения матрицы
планирования и диаграмм рассеяния, выделения
существенных вкладов факторов и их
взаимодействий, оценки коэффициентов уравнения
регрессии и статистического анализа результатов.
Исследуемые факторы должны быть смешаны
случайным образом. Полученный ряд случайно
смешанных факторов разбивают на группы по
четыре-шесть, плюс остаток, если их общее число не
кратно четырем-шести.
10

11. МЕТОД СЛУЧАЙНОГО БАЛАНСА

Факторы обычно варьируют на двух уровнях,
устанавливая каждому основной уровень Xi0 и интервал
варьирования Hi. Взяв за основу подходящую матрицу
ПФЭ или ДФЭ, для каждой группы строят матрицу ПФЭ
(ДФЭ).
Общую матрицу планирования отсеивающего
эксперимента образуют в результате последовательной
стыковки групповых матриц путем смешивания
случайным образом строк добавляемой матрицы. При
этом следят за тем, чтобы среди ее столбцов не было
двух с полностью совпадающими и с полностью
противоположными знаками.
После реализации эксперимента производится
перестройка матрицы в порядке возрастания значений
отклика (матрица ранжируется).
11

12. МЕТОД СЛУЧАЙНОГО БАЛАНСА

По ранжированной матрице находят частные медианы
Ме{Y} отдельно для случайных результатов на
верхнем (Me{Y}xi = +1) и нижнем (Me{Y}xi = -1)
уровнях каждого фактора.
При четном числе опытов N по каждому столбцу
отсчитывают сверху N/4 плюсов и записывают
соответствующий результат. Далее берут результат
следующего за этим опыта на верхнем уровне данного
фактора.
Среднеарифметическое из этих двух результатов
будет Me{Y}xi =+1. Аналогично рассчитывают
Me{Y}xi = -1. Затем рассчитывают вклад фактора Xi в
отклик Y или эффект фактора по выражению
Bxi = ( Me{Y}xi = +1 ) - ( Me{Y}xi = -1 ).
12

13. МЕТОД СЛУЧАЙНОГО БАЛАНСА

Численное сравнение вкладов факторов дает
возможность обнаружить среди них наиболее
существенные.
Для получения более достоверных результатов,
используя диаграмму рассеяния, определяют число
выделяющихся точек Тxi и вычисляют критерий Gxi по
формуле
Gxi = Bxi∙Txi .
При Gxi > 0 фактор считается существенным.
13