Аксонометрические проекции

1.

АУ «Сургутский политехнический колледж»
Преподаватель: Баева С.И.

2.

Введение
Основой построения изображений на чертеже является
прямоугольное (ортогональное) проецирование.
Предмет располагают перед плоскостью проекций так, чтобы
большинство его линий и плоских поверхностей (например,
ребра и грани параллелепипеда) были параллельны этой
плоскости.
Тогда эти линии и поверхности будут изображаться на
плоскости проекций в действительном виде без искажения.
Основные требования к чертежам:
• Обратимость: по чертежу можно изготовить изображённый предмет;
• Наглядность: по чертежу можно представить предмет;
• Относительная простота графического построения.
2

3.

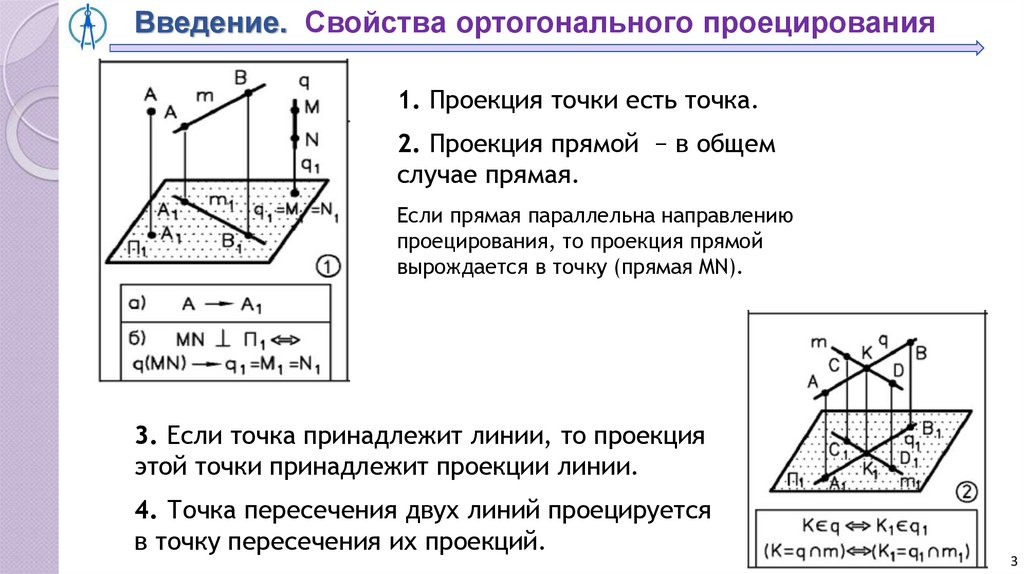
Введение. Свойства ортогонального проецирования
1. Проекция точки есть точка.
2. Проекция прямой − в общем
случае прямая.
Если прямая параллельна направлению
проецирования, то проекция прямой
вырождается в точку (прямая MN).
3. Если точка принадлежит линии, то проекция
этой точки принадлежит проекции линии.
4. Точка пересечения двух линий проецируется
в точку пересечения их проекций.
3

4.

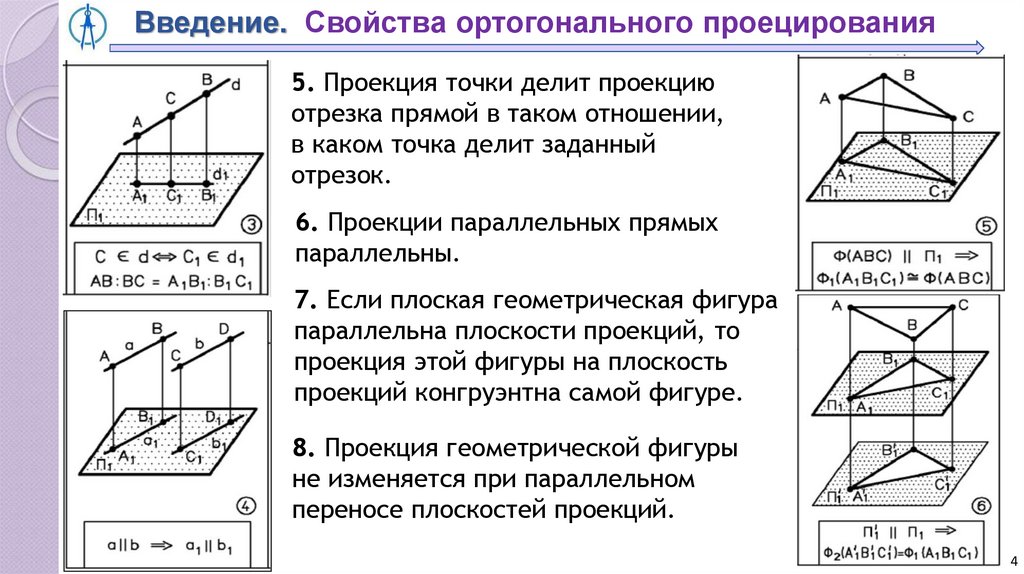
Введение. Свойства ортогонального проецирования
5. Проекция точки делит проекцию
отрезка прямой в таком отношении,
в каком точка делит заданный
отрезок.
6. Проекции параллельных прямых
параллельны.
7. Если плоская геометрическая фигура
параллельна плоскости проекций, то
проекция этой фигуры на плоскость
проекций конгруэнтна самой фигуре.
8. Проекция геометрической фигуры
не изменяется при параллельном
переносе плоскостей проекций.
4

5.

Аксонометрические проекции
Перед построением аксонометрической проекции рекомендуется изучить
ГОСТ или учебник (Короев, Ю. И. Черчение для строителей : учебник / Ю.
И. Короев. — Москва : КноРус, 2020. — 256 с. — Текст : электронный // ЭБС
КноРус : [сайт]. — URL: https://book.ru/book/932731 (дата обращения:
12.11.2019).Глава V. Аксонометрические изображения
Стр. 56.).
.
Аксонометрическими проекциями называют наглядные изображения
объекта, получаемые параллельным проецированием его на одну
плоскость проекций вместе с осями прямоугольных координат, к которым
этот объект отнесён.
Стандарт рекомендует применять пять видов аксонометрических проекций
(две прямоугольные и три косоугольные).
5

6.

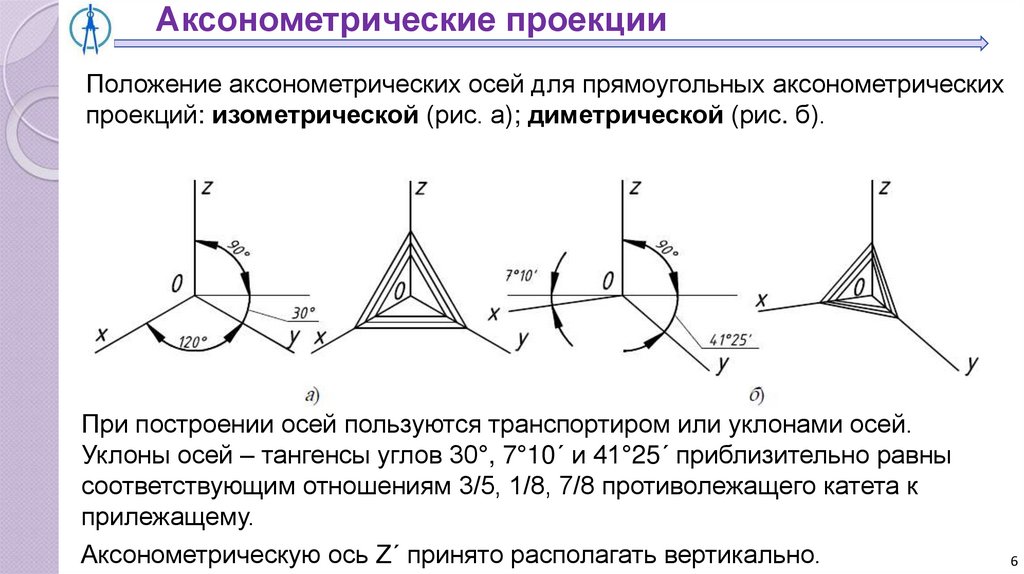
Аксонометрические проекции
Положение аксонометрических осей для прямоугольных аксонометрических
проекций: изометрической (рис. а); диметрической (рис. б).
При построении осей пользуются транспортиром или уклонами осей.
Уклоны осей – тангенсы углов 30°, 7°10´ и 41°25´ приблизительно равны
соответствующим отношениям 3/5, 1/8, 7/8 противолежащего катета к
прилежащему.
Аксонометрическую ось Z´ принято располагать вертикально.
6

7.

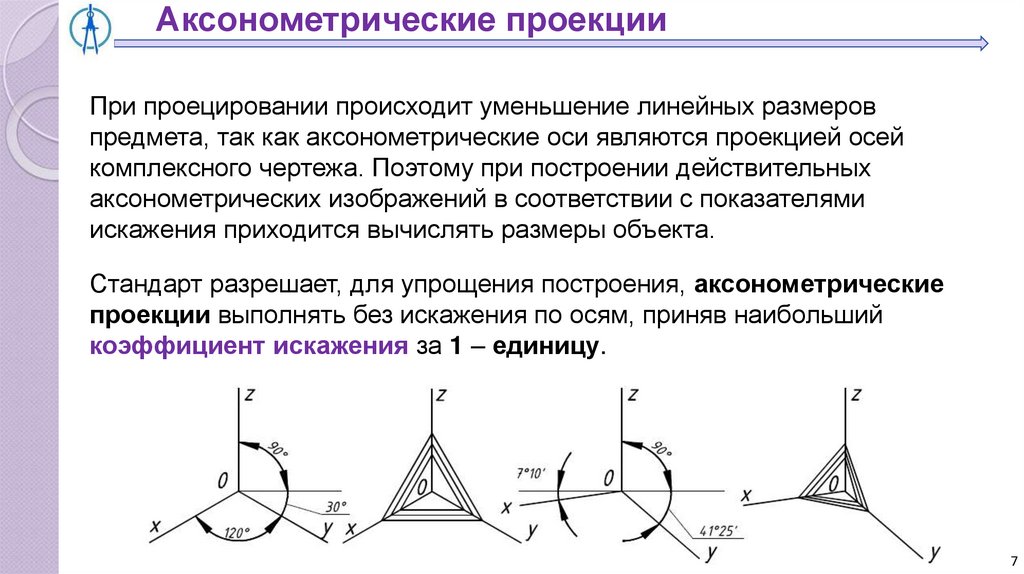
Аксонометрические проекции
При проецировании происходит уменьшение линейных размеров
предмета, так как аксонометрические оси являются проекцией осей
комплексного чертежа. Поэтому при построении действительных
аксонометрических изображений в соответствии с показателями
искажения приходится вычислять размеры объекта.
Стандарт разрешает, для упрощения построения, аксонометрические
проекции выполнять без искажения по осям, приняв наибольший
коэффициент искажения за 1 – единицу.
7

8.

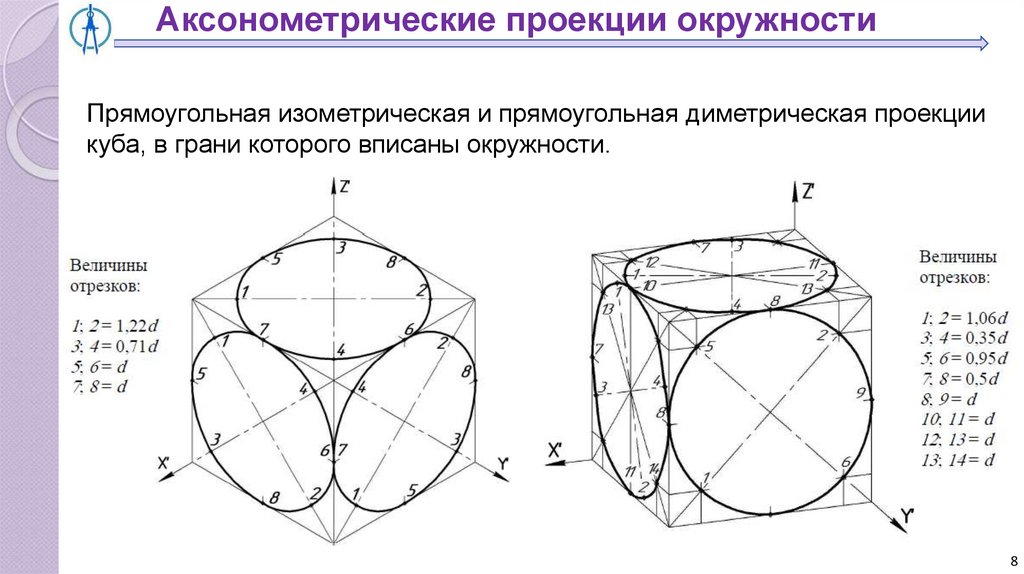
Аксонометрические проекции окружности
Прямоугольная изометрическая и прямоугольная диметрическая проекции
куба, в грани которого вписаны окружности.
8

9.

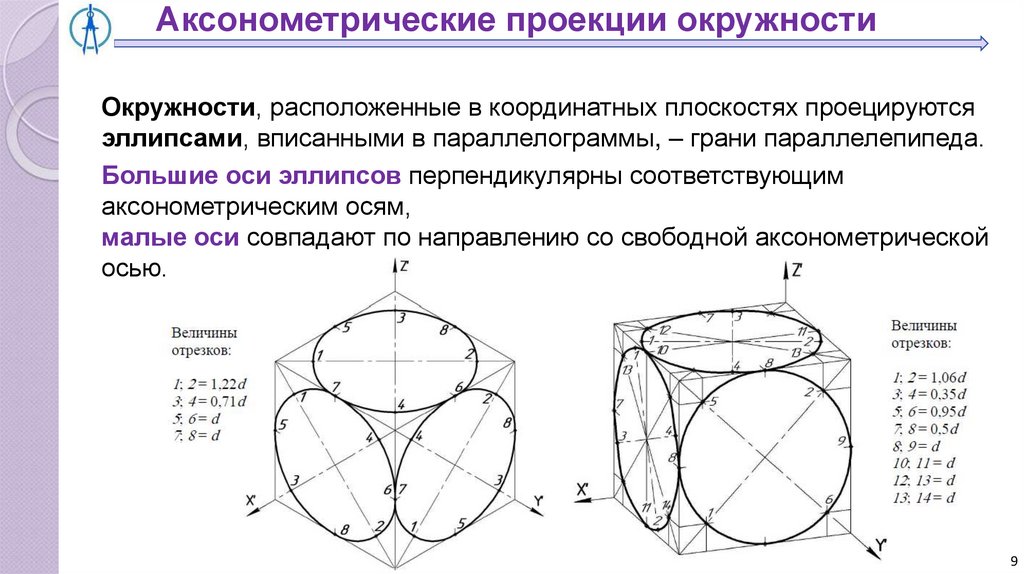
Аксонометрические проекции окружности
Окружности, расположенные в координатных плоскостях проецируются
эллипсами, вписанными в параллелограммы, – грани параллелепипеда.
Большие оси эллипсов перпендикулярны соответствующим
аксонометрическим осям,
малые оси совпадают по направлению со свободной аксонометрической
осью.
9

10.

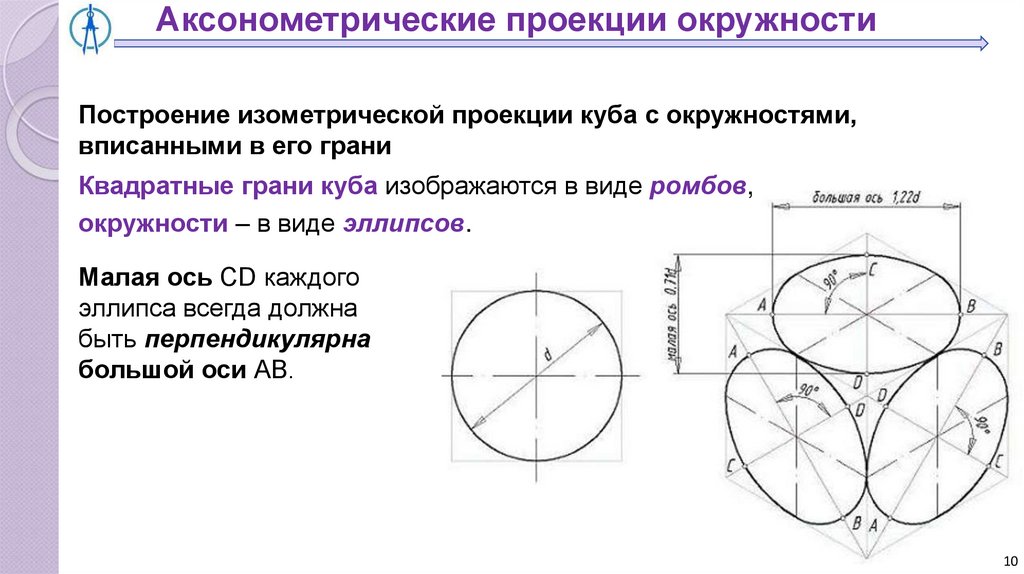
Аксонометрические проекции окружности
Построение изометрической проекции куба с окружностями,
вписанными в его грани
Квадратные грани куба изображаются в виде ромбов,
окружности – в виде эллипсов.
Малая ось СD каждого
эллипса всегда должна
быть перпендикулярна
большой оси АВ.
10

11.

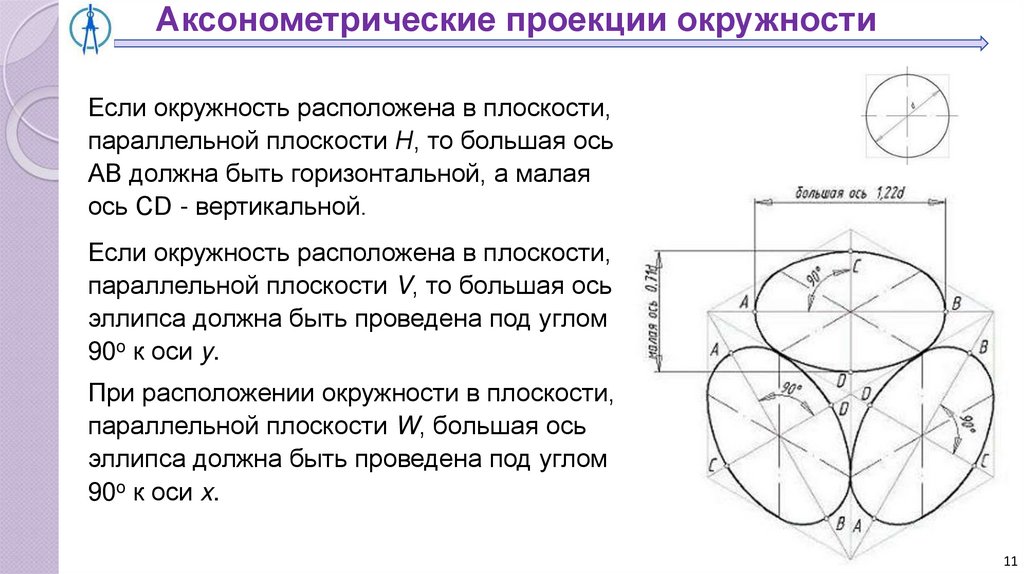
Аксонометрические проекции окружности
Если окружность расположена в плоскости,
параллельной плоскости Н, то большая ось
АВ должна быть горизонтальной, а малая
ось СD - вертикальной.
Если окружность расположена в плоскости,
параллельной плоскости V, то большая ось
эллипса должна быть проведена под углом
90o к оси y.
При расположении окружности в плоскости,
параллельной плоскости W, большая ось
эллипса должна быть проведена под углом
90o к оси x.
11

12.

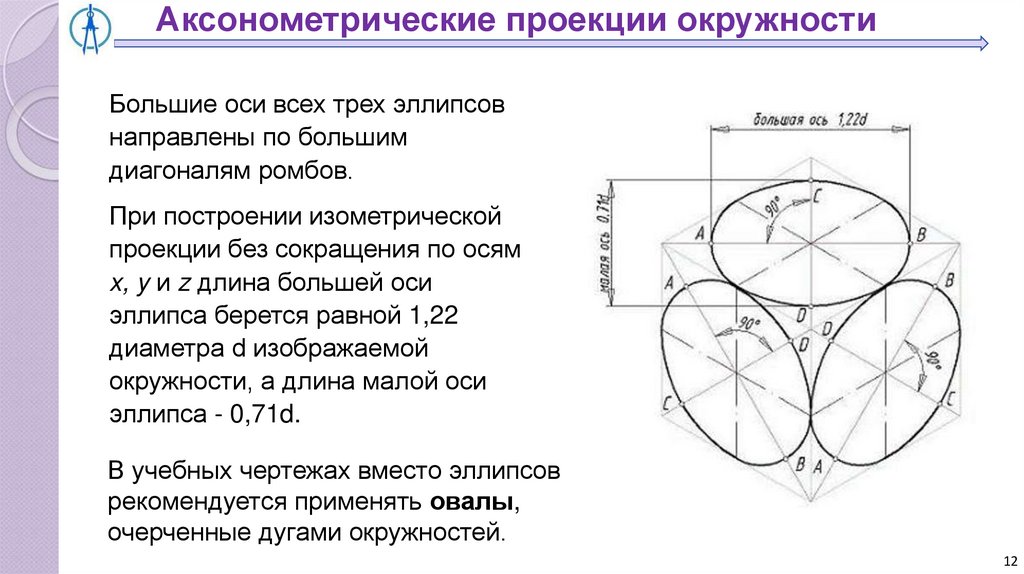
Аксонометрические проекции окружности
Большие оси всех трех эллипсов
направлены по большим
диагоналям ромбов.
При построении изометрической
проекции без сокращения по осям
x, y и z длина большей оси
эллипса берется равной 1,22
диаметра d изображаемой
окружности, а длина малой оси
эллипса - 0,71d.
В учебных чертежах вместо эллипсов
рекомендуется применять овалы,
очерченные дугами окружностей.
12

13.

Аксонометрические проекции окружности
Вычерчивание овалов
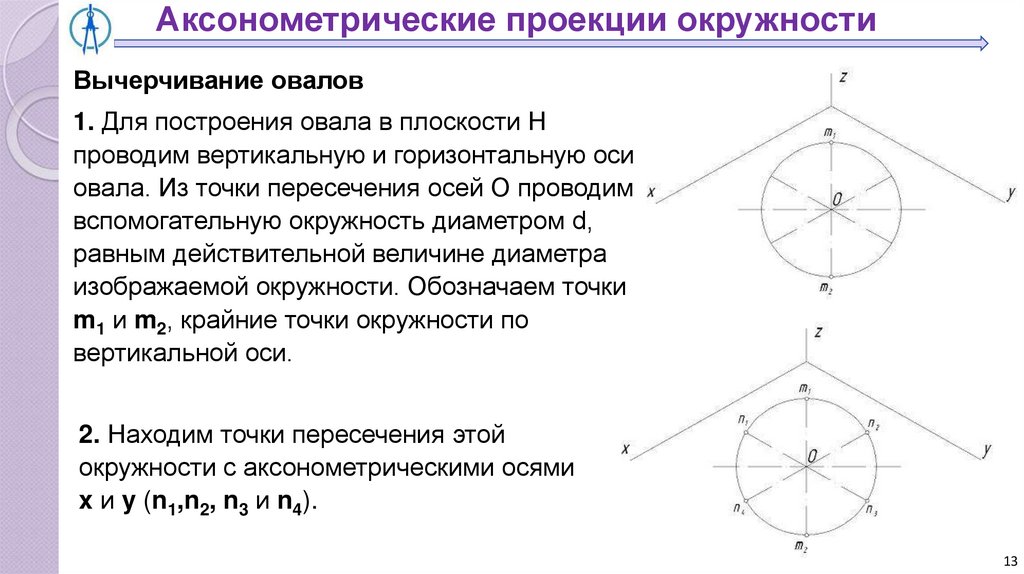
1. Для построения овала в плоскости Н
проводим вертикальную и горизонтальную оси
овала. Из точки пересечения осей О проводим
вспомогательную окружность диаметром d,
равным действительной величине диаметра
изображаемой окружности. Обозначаем точки
m1 и m2, крайние точки окружности по
вертикальной оси.
2. Находим точки пересечения этой
окружности с аксонометрическими осями
x и y (n1,n2, n3 и n4).
13

14.

Аксонометрические проекции окружности
Вычерчивание овалов
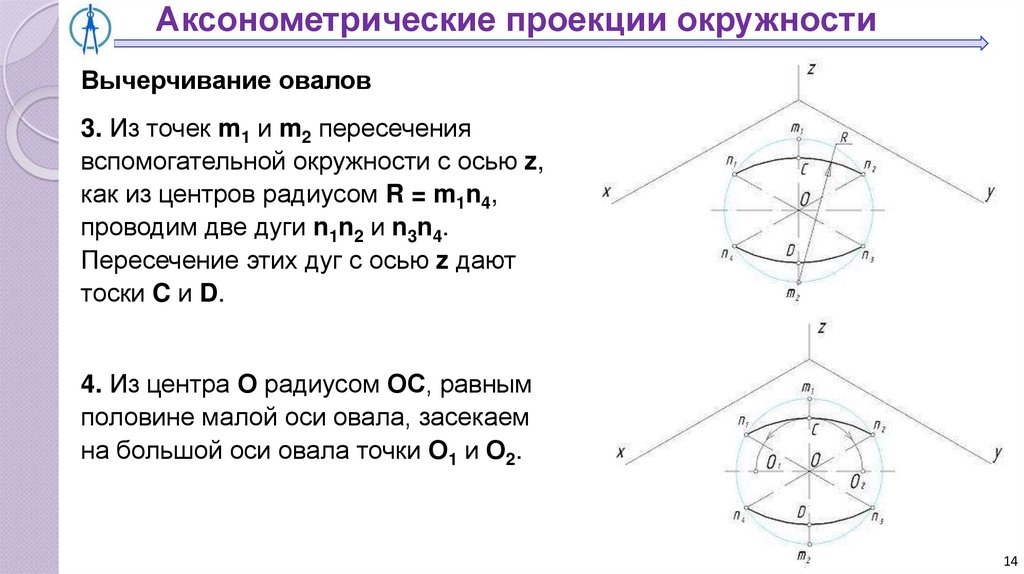
3. Из точек m1 и m2 пересечения
вспомогательной окружности с осью z,
как из центров радиусом R = m1n4,
проводим две дуги n1n2 и n3n4.
Пересечение этих дуг с осью z дают
тоски C и D.
4. Из центра О радиусом ОС, равным
половине малой оси овала, засекаем
на большой оси овала точки О1 и О2.
14

15.

Аксонометрические проекции окружности
Вычерчивание овалов
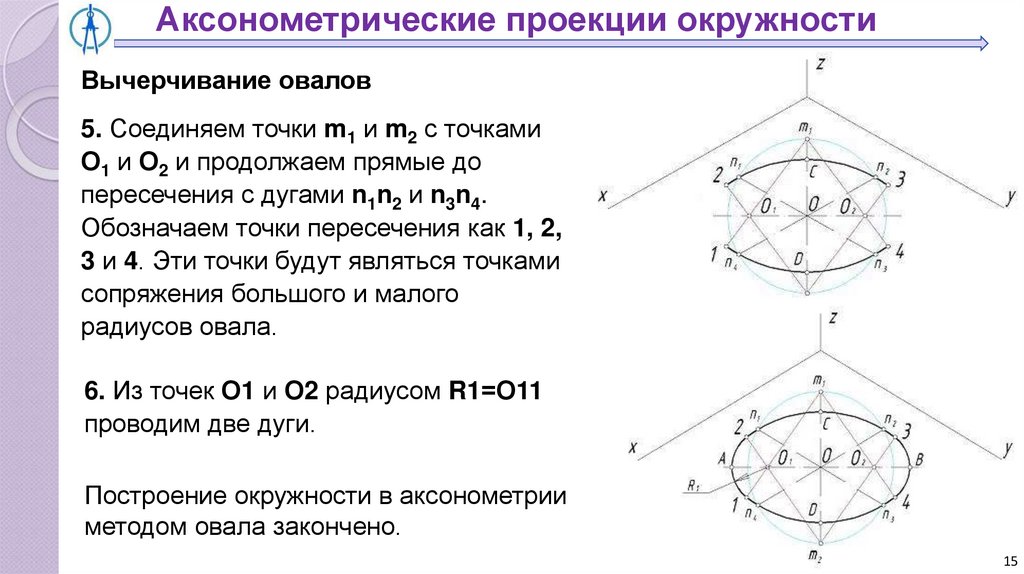
5. Соединяем точки m1 и m2 с точками
О1 и О2 и продолжаем прямые до
пересечения с дугами n1n2 и n3n4.
Обозначаем точки пересечения как 1, 2,
3 и 4. Эти точки будут являться точками
сопряжения большого и малого
радиусов овала.
6. Из точек О1 и О2 радиусом R1=О11
проводим две дуги.
Построение окружности в аксонометрии
методом овала закончено.
15