Гидрологические расчеты. Расчет среднегодовых расходов воды заданной обеспеченности (Лекция 2)

1.

Для студентов III курса
гидрологического факультета РГГМУ
к.г.н., доц. Сикан Александр Владимирович

2.

При решении многих гидрологических задач
необходимо знать не только норму годового стока, но и
среднегодовые расходы воды различной
обеспеченности (ежегодной вероятности превышения).
В частности такая необходимость возникает при
проектировании водозаборов, при водохозяйстенном
планировании, при проведении мероприятий по
защите и охране водных объектов и др.
2

3.

Для определения расходов заданной вероятности ежегодного
превышения используются аналитические кривые обеспеченностей.
Аналитические кривые позволяют сгладить эмпирические кривые и
провести экстраполяцию в область больших и малых обеспеченностей.
3,5
Эмпирическая
Модульный коэффициент
3,0
Крицкого-Менкеля
2,5
2,0
1,5
1,0
0,5
0,0
0,01
0,1
0,5 1
3 5
10
20 30 40 50 60 70 80
90 95 97
99
99,9 99,99
Обеспеченность, P %
3

4.

Эмпирические и аналитические кривые обеспеченностей
обычно строят на клетчатках вероятностей.
Эмпирическую обеспеченность определяют по формуле:
Pm,%
m
100%,
n 1
В качестве аналитических кривых при расчетах годового
стока в Росси наиболее часто используются
трехпараметрические кривые обеспеченностей
Крицкого-Менкеля и Пирсона III типа.
4

5.

Основные этапы расчета:
1. Предварительный анализ исходных данных.
2. Проверка ряда на случайность.
3. Проверка ряда на однородность.
4. Расчет параметров распределения.
5. Расчет погрешностей параметров распределения.
6. Построение эмпирической и аналитической кривых
обеспеченностей.
5

6.

1.1.1. Предварительный анализ исходных данных
Производится анализ надежности экстраполяции кривой Q = f(H).
Выполняется проверка полноты учета стока воды на поймах и в
протоках.
Оценивается точность расчета стока за различные интервалы
времени.
На этом же этапе рекомендуется построить хронологический
график и оценить значимость тренда.
Цель такой проверки – оценить надежность исходной информации
и выявить грубые ошибки и опечатки.
6

7.

1.1.2. Проверка ряда на случайность
Коэффициент автокорреляции незначим если
r (1) r t
(1)
i n 1
r (1)
( xi x)( xi 1 x)
i 1
(2)
(n 2) Dx
1 r (1)
r
n 2
2
(3)
7

8.

Еще один вариант оценки значимости коэффициента автокорреляции
n 1
Выборочный
коэффициент
автокорреляции:
x
i
x1 xi 1 x2
i 1
r
n 1
x
x1
2
i
i 1
,
n 1
x
i 1
n 1
n 1
x2
2
x
x1
i 1
n 1
x
i 1
i
,
x2
i 1
n 1
.
i 1
Статистика r распределена асимптотически нормально с математическим
ожиданием и СКО:
mr 1 /( n 1)
Коэффициент
автокорреляции не значим если:
r
n(n 3)
.
2
(n 1)(n 1)
r mr
r
t1 ,
где t1- – квантиль стандартного нормального распределения; 2 – двухсторонний уровень значимости.
8

9.

1.1.3. Проверка ряда на однородность*
Проверка однородности гидрологического ряда
по дисперсии (критерий Фишера)
D1
*
F
D2
F* F
2
(1)
(2)
Проверка однородности гидрологического ряда
по среднему значению (критерий Стьюдента)
*
t (Q1 Q 2 )
(n1 1) 12 (n2 1) 22
n1 n2 2
t* t
2
nn
1 2
n1 n2
(3)
(4)
9

10.

Коэфф. автокорреляции
10

11.

Коэфф. автокорреляции
11

12.

1.1.4. Расчет параметров распределения
Обычно рассчитываются среднее значение ряда,
коэффициент вариации и коэффициент асимметрии.
Расчет производится методом моментов.
Если коэффициент вариации больше 0,6, следует
произвести уточнение указанных характеристик,
используя метод наибольшего правдоподобия.
12

13.

Метод моментов
1 n
x xi
n i 1
n
Cv
x
2
k
1
i
i 1
n 1
n
Cs
n ki 1
3
i 1
(n 1)(n 2)Cv3
13

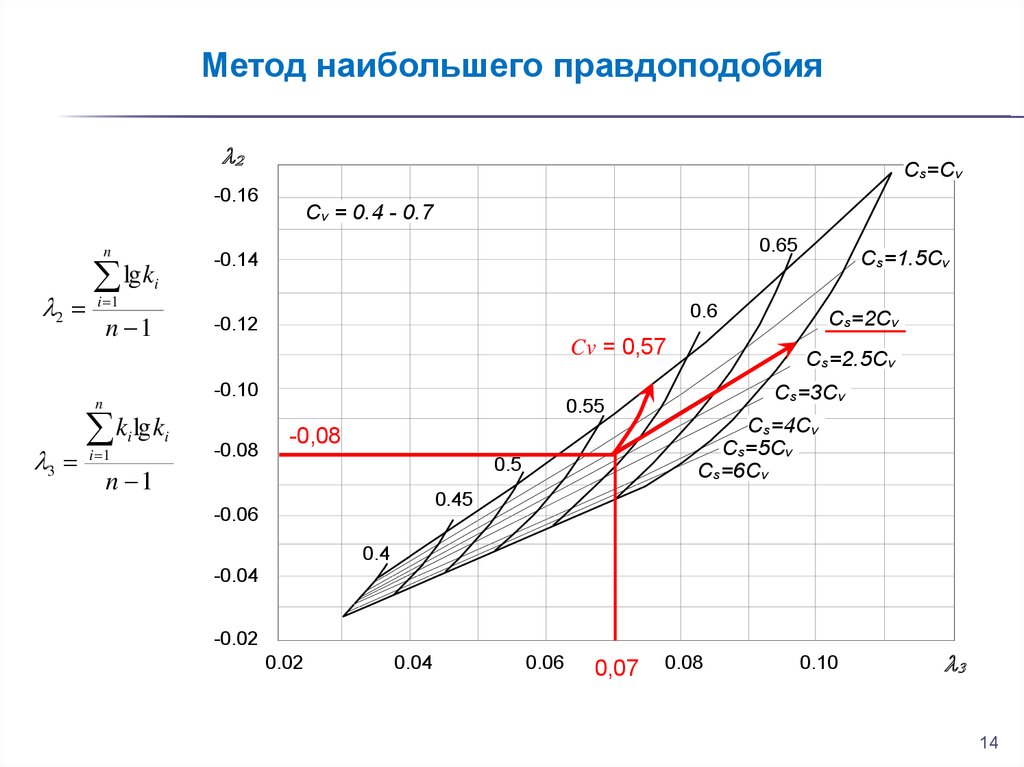
14.

Метод наибольшего правдоподобия
Cs=Cv
-0.16
n
2
lg ki
-0.14
n 1
-0.12
0.65
i 1
-0.10
k lg k
i 1
i
i
-0.08
Cs=1.5Cv
0.6
Cv = 0,57
n
3
Cv = 0.4 - 0.7
0.55
-0,08
0.5
n 1
Cs=2Cv
Cs=2.5Cv
Cs=3Cv
Cs=4Cv
Cs=5Cv
Cs=6Cv
0.45
-0.06
0.4
-0.04
-0.02
0.02
0.04
0.06
0,07
0.08
0.10
14

15.

Если для описания вероятностной структуры
гидрологических рядов используется модель авторегрессии
первого порядка и при этом Cv > 0,6, то значение
коэффициента вариации корректируется по формуле:
a ~
a
a ~
Cv a1 2 a3 4 Cv a5 6 Cv2
n
n
n
a1 ……a6 = f [Cs/Cv, r(1)]
15

16.

Значения коэффициентов a в формуле (*)
(табл. Б.1 СП 33-101-2003)
Значение
Cs / Cv
2
3
4
Коэффициенты
r(1)
a1
a2
a3
a4
a5
a6
0
0
0,19
0,99
-0,88
0,01
1,54
0,3
0
0,22
0,99
-0,41
0,01
1,51
0,5
0
0,18
0,98
0,41
0,02
1,47
0
0
0,69
0,98
-4,34
0,01
6,78
0,3
0
1,15
1,02
-7,53
-0,04
12,38
0,5
0
1,75
1,00
-11,79
-0,05
21,13
0
0
1,36
1,02
-9,68
-0,05
15,55
0,3
-0,02
2,61
1,13
-19,85
-0,22
34,15
0,5
-0,02
3,47
1,18
-29,71
-0,41
58,08
a ~
a
a ~
Cv a1 2 a3 4 Cv a5 6 Cv2
n
n
n
(*)
16

17.

1.1.5. Расчет погрешностей параметров распределения
x
Cv
Cv 1 r
100%
n 1 r
n(1 Cv2 ) 3Cv r 2
1
100 %
2
1 r
(2)
(6 / n)(1 6Cv2 5Cv4 ) 100 %
(3)
1
n 4Cv2
1
cs
Cs
(1)
1
cs
Cs
(6 / n)(1 Cv2 ) 100 %
(4)
17

18.

1.1.6. Построение эмпирической и аналитической кривых
обеспеченностей
Для построения эмпирической кривой обеспеченностей значения
исходного ряда ранжируются (располагаются в убывающем
порядке). Затем для каждого члена ранжированного ряда (xm)
рассчитывается эмпирическая обеспеченность по формуле:
Pm,%
m
100%,
n 1
Ординаты аналитической кривой обеспеченностей вычисляют в
зависимости от параметров:
QP % f ( P%, x, Cv, Cs)
18

19.

Нормированные ординаты кривой обеспеченностей Пирсона III типа, tp = f (Cs, p);
(фрагмент таблицы)
Cs
–1.8
–1.6
–1.4
–1.2
–1.0
–0.8
–0.6
–0.4
–0.2
0.0
0.2
0.4
0.6
tp
Обеспеченность, p %
0.01
1.11
1.26
1.41
1.68
1.92
2.23
2.57
2.98
3.37
3.72
4.16
4.61
5.05
(xp x)
0.1
1.11
1.24
1.39
1.58
1.79
2.02
2.27
2.54
2.81
3.09
3.38
3.66
3.96
1.0
1.09
1.20
1.32
1.45
1.59
1.74
1.88
2.03
2.18
2.33
2.47
2.61
2.75
(k p 1)
Cv
5.0
1.02
1.10
1.17
1.24
1.32
1.38
1.45
1.52
1.58
1.64
1.70
1.75
1.80
10
0.94
0.99
1.04
1.08
1.13
1.17
1.20
1.23
1.26
1.28
1.30
1.32
1.33
20
0.80
0.81
0.83
0.84
0.85
0.86
0.85
0.85
0.85
0.84
0.83
0.82
0.80
x p t p x
25
0.72
0.73
0.73
0.74
0.73
0.73
0.72
0.71
0.69
0.67
0.65
0.63
0.61
30
0.64
0.64
0.64
0.63
0.62
0.60
0.59
0.57
0.55
0.52
0.50
0.47
0.44
50
0.28
0.25
0.22
0.19
0.16
0.13
0.10
0.07
0.03
0.00
–0.03
–0.07
–0.10
k p t p Cv 1
19

20.

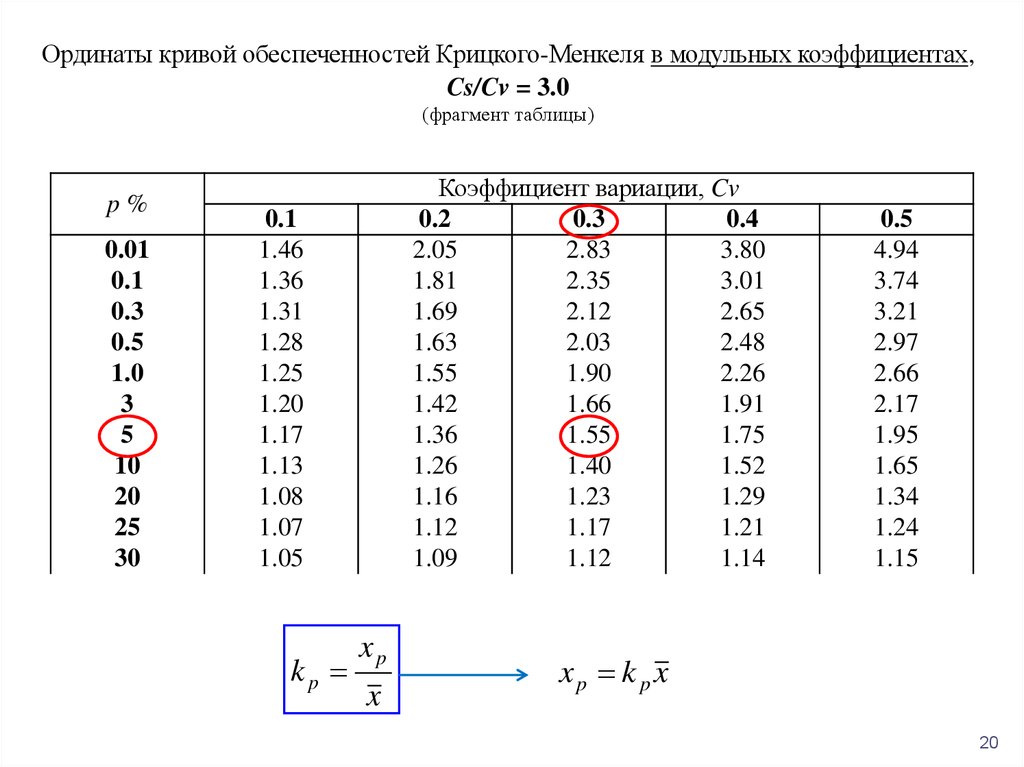
Ординаты кривой обеспеченностей Крицкого-Менкеля в модульных коэффициентах,
Cs/Cv = 3.0
(фрагмент таблицы)
p%
0.01
0.1
0.3
0.5
1.0
3
5
10
20
25
30
Коэффициент вариации, Cv
0.2
0.3
0.4
2.05
2.83
3.80
1.81
2.35
3.01
1.69
2.12
2.65
1.63
2.03
2.48
1.55
1.90
2.26
1.42
1.66
1.91
1.36
1.55
1.75
1.26
1.40
1.52
1.16
1.23
1.29
1.12
1.17
1.21
1.09
1.12
1.14
0.1
1.46
1.36
1.31
1.28
1.25
1.20
1.17
1.13
1.08
1.07
1.05
kp
xp
x
0.5
4.94
3.74
3.21
2.97
2.66
2.17
1.95
1.65
1.34
1.24
1.15
xp k p x
20

21.

3,5
Эмпирическая
3,0
Модульный коэффициент
Пирсона III типа
2,5
2,0
1,5
1,0
0,5
0,0
0,01
0,1
0,5 1
3
5
10
20
30 40 50 60 70
80
90
95 97
99 99,5
99,9
99,99
Обеспеченность, P %
Если аналитическая кривая хорошо аппроксимирует эмпирические точки, то
ординаты аналитической кривой принимаются в качестве расчетных значений.
21

22.

При недостаточности данных гидрометрических наблюдений используется
метод гидрологической аналогии.
р. Лжа – д. Фелицианово, Q м 3/с
8,0
y = 0,23x + 0,17
R² = 0,79
7,0
6,0
Строится график связи среднегодовых
расходов расчетной реки и реки-аналога
за совместный период наблюдений.
5,0
4,0
3,0
2,0
1,0
0,0
0
5
10
15
20
25
30
35
р. Утроя – д. Большая Губа, Q м 3/с
Связь считается надежной если выполнены условия
n ≥ 6;
| R | ≥ 0,7;
R
R
2;
a
a
2
22

23.

Первый вариант расчета
При использовании этого варианта расчета приведение к длинному ряду
аналога выполняется только для параметров распределения.
Ряд расходов не удлиняется.
Средний многолетний расход расчетной реки, приведенный к длинному ряду реки-аналога
определяется по формуле (1) или по формуле (2)
Q N aQ N , a b
Q N Qn R
(1)
n
(Q Q n,a )
n,a N ,a
(2)
Коэффициент вариации расчетной реки, приведенный к длинному ряду реки-аналога
определяется по формуле (3)
n
Cv , N
QN
n2,a
1 R 1 2
N .a
2
(3)
В качестве расчетного значения Cs/Cv принимается среднее районное значение.
23

24.

Второй вариант расчета
При реализации второго метода ряд расчетной реки восстанавливается по
уравнению линейной регрессии с использованием данных реки-аналога:
~
Qi a Qi ,а b
(1)
Систематическое преуменьшение дисперсии восстановленной части ряда
исключается путем корректировки погодичных значений по формуле:
~
Qi Qn
Qi
Qn
R
Qi
~
Qi
(2)
- расчетные значения расходов воды восстановленной части ряда;
- значения расходов, полученные по уравнению регрессии;
Qn - среднее значение расхода расчетной реки за совместный период наблюдений.
24

25.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
…
37
38
1945
1946
1947
1948
1949
1950
1951
1952
1953
1954
1955
1956
1957
1958
1959
1960
1961
1962
1963
1964
…
1981
1982
~
Qi
6,75
4,91
2,54
3,87
3,69
3,90
3,92
4,17
5,05
2,70
4,95
6,08
5,92
…
Приведение ряда среднегодовых
расходов воды (м3/с) расчетной
реки к длинному ряду реки-аналога
Qi
7,15
5,08
2,42
3,92
3,71
3,94
3,97
4,25
5,23
2,60
5,13
6,40
6,22
5,66
4,73
3,43
3,29
4,98
2,54
0,75
…
4,81
4,29
Восстановленная часть ряда
Год
Расходы Расходы
реки- расчетной
аналога
реки
28,6
20,6
10,3
16,1
15,3
16,2
16,3
17,4
21,2
11,0
20,8
25,7
25,0
24,5
5,66
14,4
4,73
18,0
3,43
10,3
3,29
23,6
4,98
11,0
2,54
3,78
0,75
..
…
20,9
4,81
20,5
4,29
~
Qi a Qi ,а b
~
Q Qn
Qi i
Qn
R
(1)
(2)
Исходный ряд
№
п/п
25

26.

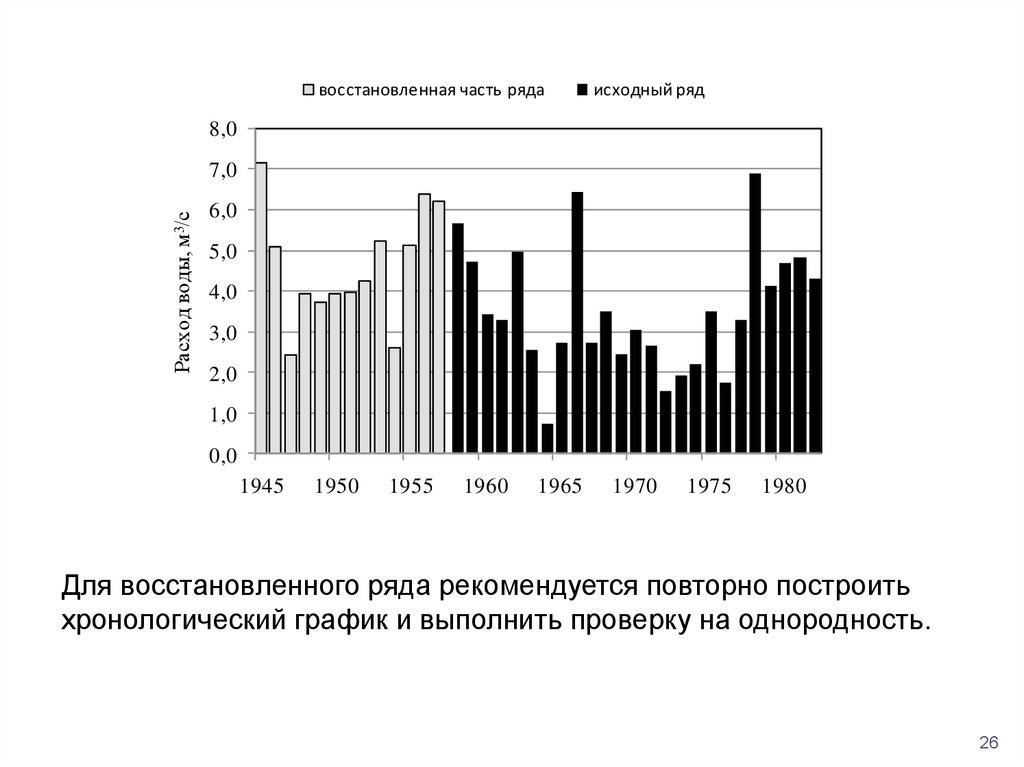
восстановленная часть ряда
исходный ряд
8,0
Расход воды, м 3/с
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
1945
1950
1955
1960
1965
1970
1975
1980
Для восстановленного ряда рекомендуется повторно построить
хронологический график и выполнить проверку на однородность.
26

27.

По удлиненному ряду рассчитываются новые значения среднего и
коэффициента вариации.
В качестве расчетного значения Cs/Cv принимается среднее районное
значение.
Допускается также подбирать Cs/Cv по наилучшему соответствию
эмпирической и аналитической кривых обеспеченностей (с округлением до 0,5).
3,0
Эмпирическая
Модульный коэффициент
2,5
Крицкого-Менкеля
Эмпирическая и аналитическая
кривые обеспеченностей
2,0
среднегодовых расходов воды в
модульных коэффициентах -
1,5
расчет по удлиненному ряду.
1,0
0,5
0,0
0,01
0,1
0,5 1
3 5
10
20 30 40 50 60 70 80
90 95 97
99
99,9 99,99
Обеспеченность, P %
27

28.

Расчет погрешностей статистических характеристик удлиненного ряда
Относительная среднеквадратическая погрешность среднего значения
восстановленного ряда определяется по формуле
Q
N
2
n
N ,a
2
1 R
1 .
2
N
n
n,a
100 n
QN
(1)
Случайные среднеквадратические погрешности восстановленного ряда
можно также определить по «обычным» формулам с учетом объема
информации, эквивалентной наблюденным данным.
N э. x
N
N n
1
1 R2
n 2
(2)
N э.
Nn
n ( N n)(1 R 4 )
где: n
– число совместных лет наблюдений в расчетном створе и в створе реки-аналога;
(N – n)
– число восстановленных членов ряда по уравнению;
R
(3)
– коэффициент парной корреляции.
28

29.

Схема расчета объема информации, эквивалентной наблюденным данным
Ряд расчетной реки
Ряд реки-аналога
Данные по
аналогу
отсутствуют
Совместный
период
наблюдений
m
n
N
Восстановленная
часть ряда
(N – n)
Nэкв.общее Nэкв m
29

30.

Для среднего
Для СКО
Объем эквиваленнто-независимой информации, Nэ
75
Длина ряда расчетной
реки n = 20 лет.
70
65
Коэффициент
корреляции для связи
среднегодовых
расходов расчетной
реки и реки-аналога
R = 0,80
60
55
50
45
Длина ряда рекианалога
N = от 30 до 100 лет
40
35
30
25
30
40
50
60
70
80
Длина ряда реки-аналога, N
90
100
График зависимости объема эквивалентно-независимой
информации от длины ряда реки-аналога при фиксированных n и R
30

31.

Метод отношений
Искомый
расход
Qi ,a
Qi
QP % QP %, a
Q2012 Q2012,a
Q1%
Q1%, a
QP % Qi
QP %, a
Qi ,a
Q1% Q2012
Q1%, a
Q2012,a
31

32.

При отсутствии наблюдений за стоком в расчетном створе среднее
значение и коэффициент вариации определяются следующими методами:
1. Осреднение по ближайшим пунктам-аналогам.
2. Пространственная интерполяция.
3. Использование карт изолиний.
Расчетные значения Cs/Cv следует принимать как среднее из
значений, установленных по данным группы рек с наиболее
продолжительными рядами в гидрологически однородном районе.
32

33.

Фрагмент карты
изолиний
коэффициента
вариации
годового стока
рек России
33

34.

2,5
2,0
Районирование
отношения Cs/Cv
для среднегодового
стока рек России
(фрагмент карты)
2,5
2,5
34

35.

К значениям нормы стока и коэффициента вариации, определенным по
картам изолиний могут вводиться поправки учитывающие влияние местных
азональных факторов.
Допускается использовать региональные зависимости нормы стока и
коэффициента вариации от метеорологических, физико-географических и
других факторов.
Пример формулы для определения коэффициента вариации (СНиП 2.01.14-83)
A
Cv
q
0, 4
F 1000 0,1
q – средний многолетний модуль годового стока, л/с км2;
F – площадь водосбора, км2.
A – параметр, определяемый по данным рек-аналогов.
35

36.

ЛИТЕРАТУРА.
Владимиров А.М. Гидрологические расчеты, с. 151-175.
Горошков И.Ф. Гидрологические расчеты, с.42-80, с. 116-168.
Методические рекомендации по определению расчетных гидрологических
характеристик при недостаточности данных гидрометрических наблюдений, с.10-26.
Методические рекомендации по определению расчетных гидрологических
характеристик при отсутствии данных гидрометрических наблюдений, с.20-27.
36