Математика 6 класс

1. Математика 6 класс

Математик
а
6 класс

2. Сложение и вычитание дробей с разными знаменателями

3.

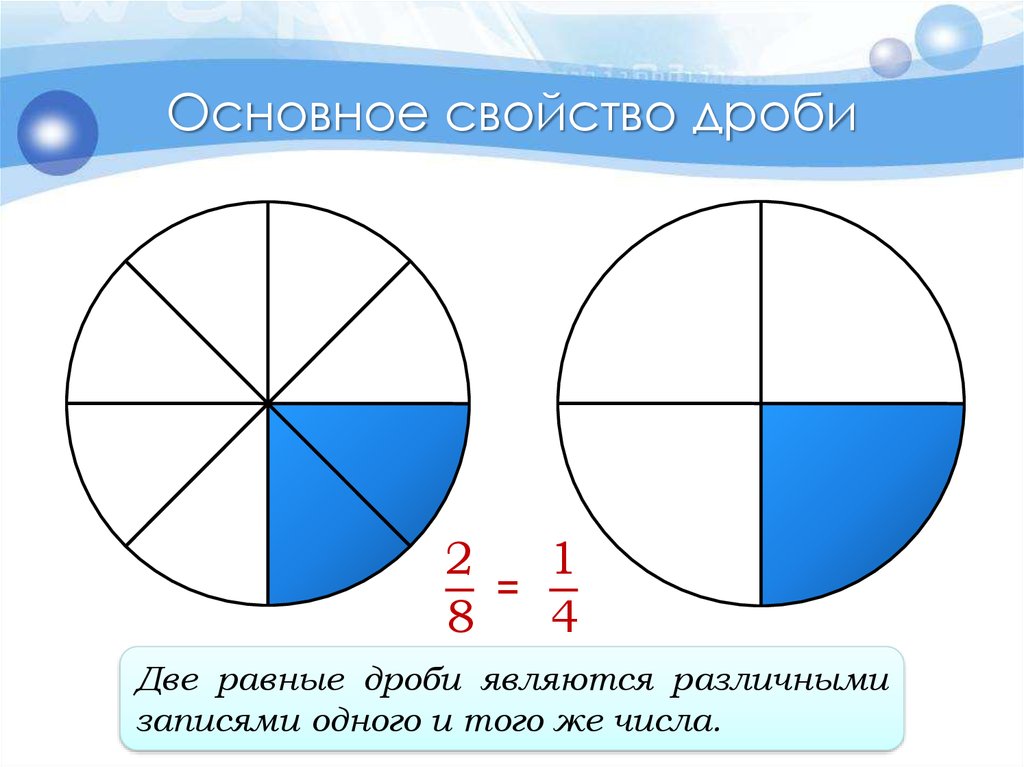
Основное свойство дроби
2
1
=
8
4
Две равные дроби являются различными
записями одного и того же числа.

4. Основное свойство дроби

Если числитель и знаменатель дроби умножить или
разделить на одно и то же натуральное число, то
получится равная ей дробь.
1 1 2 2
4 4 2 8
3
3:3 1
12 12 : 3 4
5 5 4 20
7 7 4 28
14 14 : 7 2
21 21 : 7 3

5.

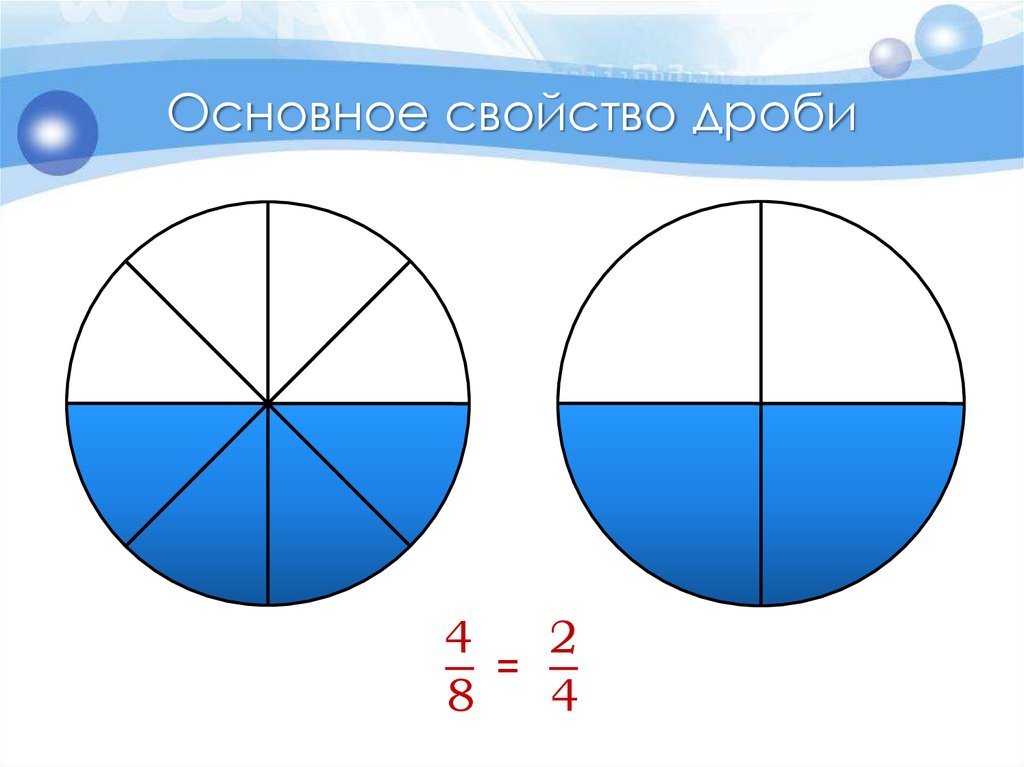
Основное свойство дроби
4
2
=
8
4

6.

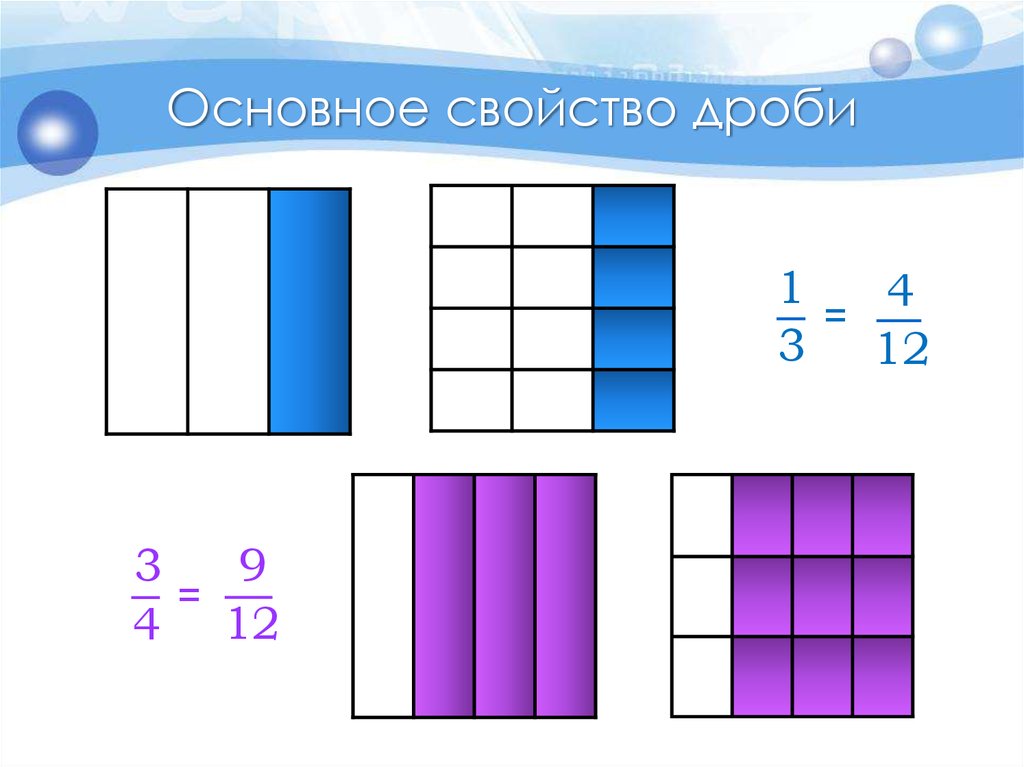
Основное свойство дроби
1
4
=
3 12
3
9
=
4 12

7. Сокращение дробей

Деление числителя и знаменателя на их общий
делитель, отличный от единицы, называют
сокращением дроби.
3
3:3 1
12 12 : 3 4
14 14 : 7 2
21 21 : 7 3
Если числитель и знаменатель дроби – взаимно
простые числа, то такую дробь называют
несократимой.

8. Сокращение дробей

Наибольшее число, на которое можно сократить
дробь, − это наибольший общий делитель ее
числителя и знаменателя.
36 36 : 12 3
48 48 : 12 4
14 14 : 7 2
21 21 : 7 3
60 60 : 30 2
90 90 : 30 3
38 38 : 19 2
95 95 : 19 5

9. Сокращение дробей разложением на множители

150 2 3 5 5 2
225 3 3 5 5 3
154
2 7 11 11
210 2 3 5 7 15
150
75
25
5
1
2
3
5
5
225
75
25
5
1
3
3
5
5
154 2 210 2
77 7 105 3
11 11 35 5
1
7 7
1

10.

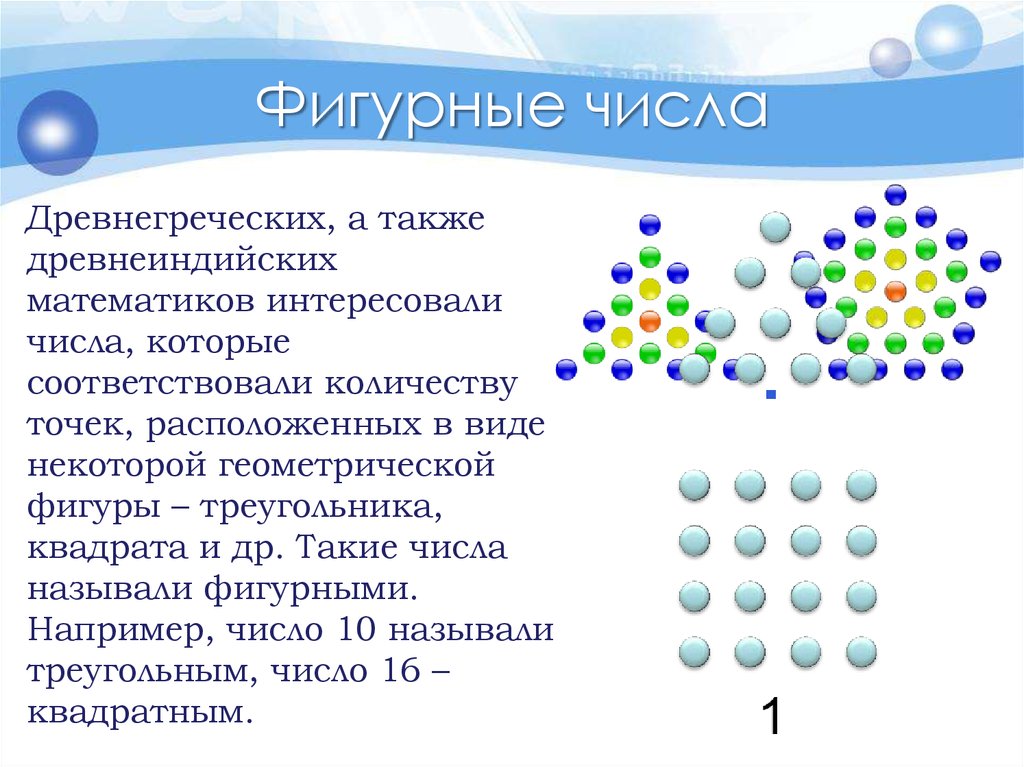
Фигурные числа
Древнегреческих, а также
древнеиндийских
математиков интересовали
числа, которые
соответствовали количеству
точек, расположенных в виде
некоторой геометрической
фигуры – треугольника,
квадрата и др. Такие числа
называли фигурными.
Например, число 10 называли
треугольным, число 16 –
квадратным.

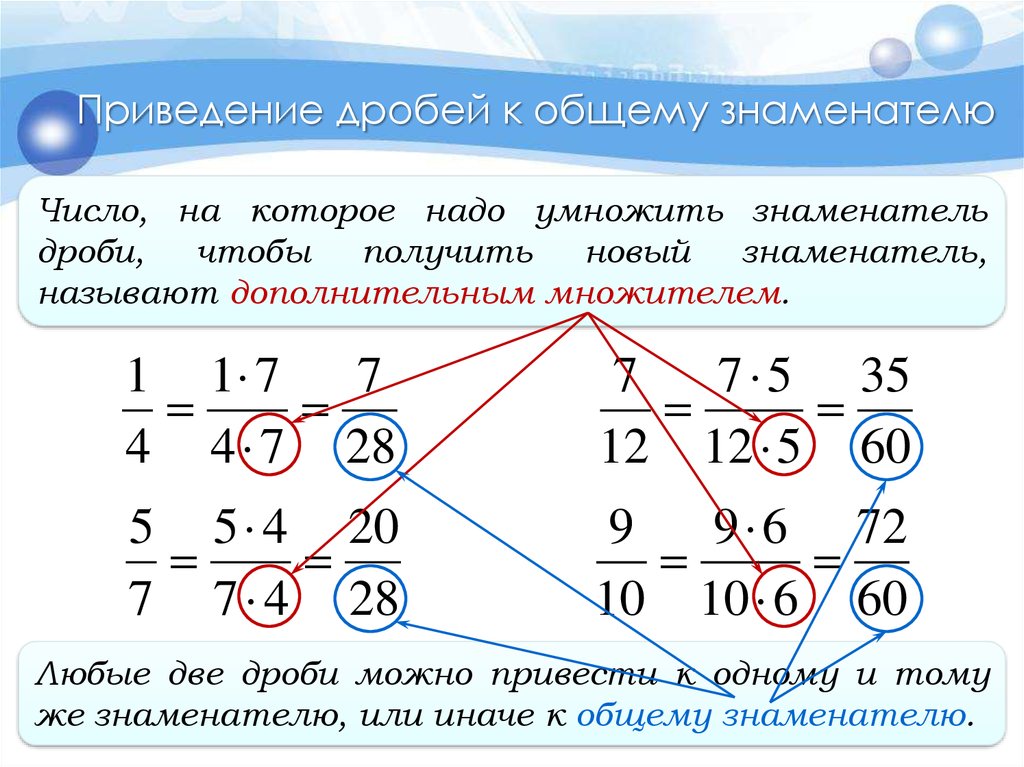
11. Приведение дробей к общему знаменателю

Число, на которое надо умножить знаменатель
дроби,
чтобы
получить
новый
знаменатель,
называют дополнительным множителем.
1 1 7
7
4 4 7 28
7
7 5 35
12 12 5 60
5 5 4 20
7 7 4 28
9
9 6 72
10 10 6 60
Любые две дроби можно привести к одному и тому
же знаменателю, или иначе к общему знаменателю.

12. Приведение дробей к общему знаменателю

Чтобы привести дроби к наименьшему общему
знаменателю, надо:
1. найти наименьшее общее кратное
знаменателей этих дробей, оно и будет их
наименьшим общим знаменателем;
2. разделить наименьший общий знаменатель на
знаменатели данных дробей, т. е. найти для
каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой
дроби на ее дополнительный множитель.

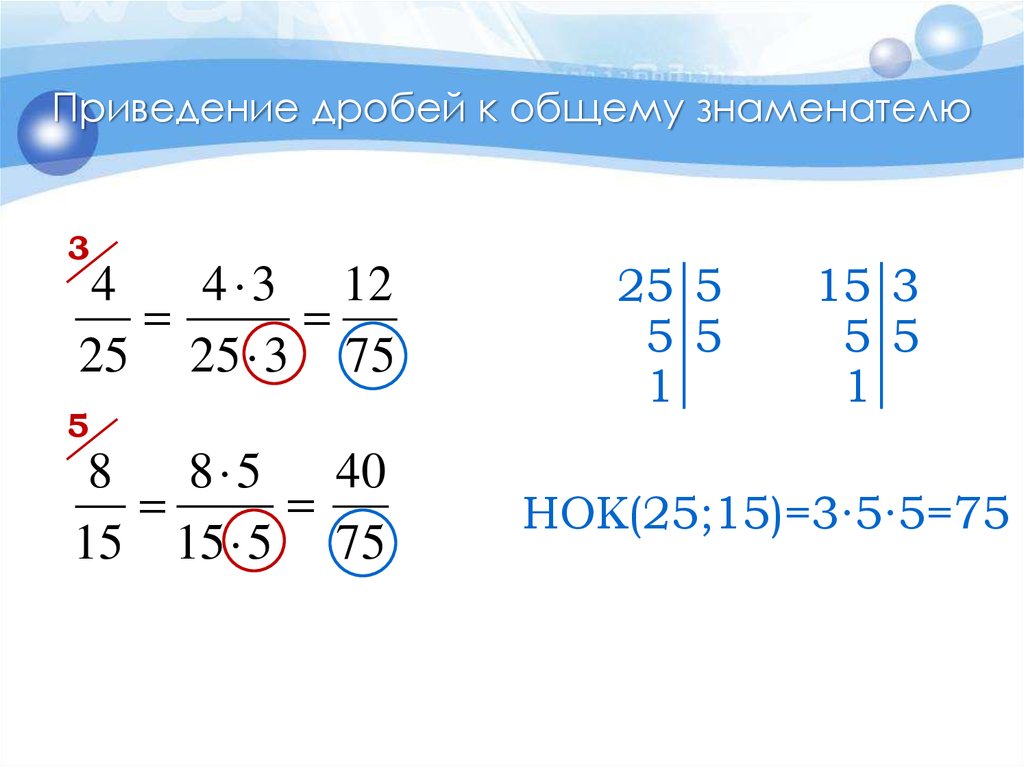
13. Приведение дробей к общему знаменателю

3
4
4 3 12
25 25 3 75
5
8 5 40
8
15 15 5 75
25 5
5 5
1
15 3
5 5
1
НОК(25;15)=3∙5∙5=75

14. Приведение дробей к общему знаменателю

5
13 13 5 65
49 49 5 245
7
5 7
35
5
35 35 7 245
49 7
7 7
1
35 5
7 7
1
НОК(49;35)=7∙7∙5=245

15. Сравнение, сложение и вычитание дробей с разными знаменателями

Чтобы сравнить (сложить или вычесть) дроби с
разными знаменателями, надо:
1) привести данные дроби к наименьшему общему
знаменателю;
2) сравнить (сложить или вычесть) полученные
дроби.

16. Сравнение дробей с разными знаменателями

4
8
Сравните:
и
25
15
3
5
4
4 3 12
25 25 3 75
12
75
<
40
75
8
8 5 40
15 15 5 75
⇒
4
25
8
< 15

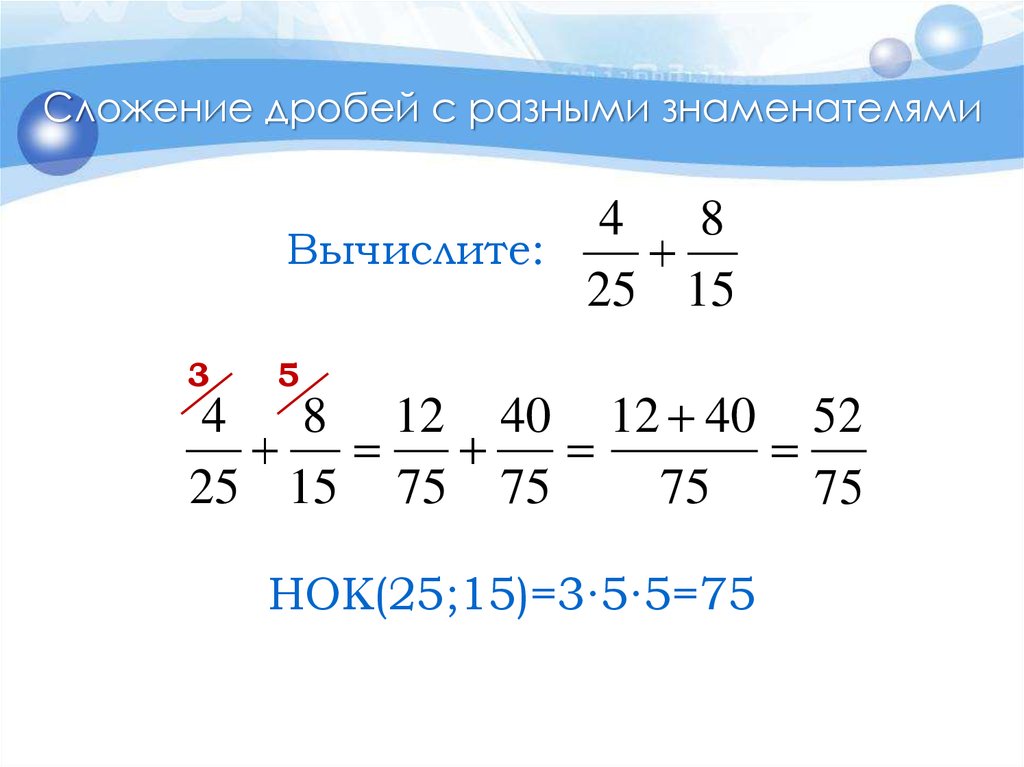
17. Сложение дробей с разными знаменателями

4 8
Вычислите:
25 15
3
5
4 8 12 40 12 40 52
25 15 75 75
75
75
НОК(25;15)=3∙5∙5=75

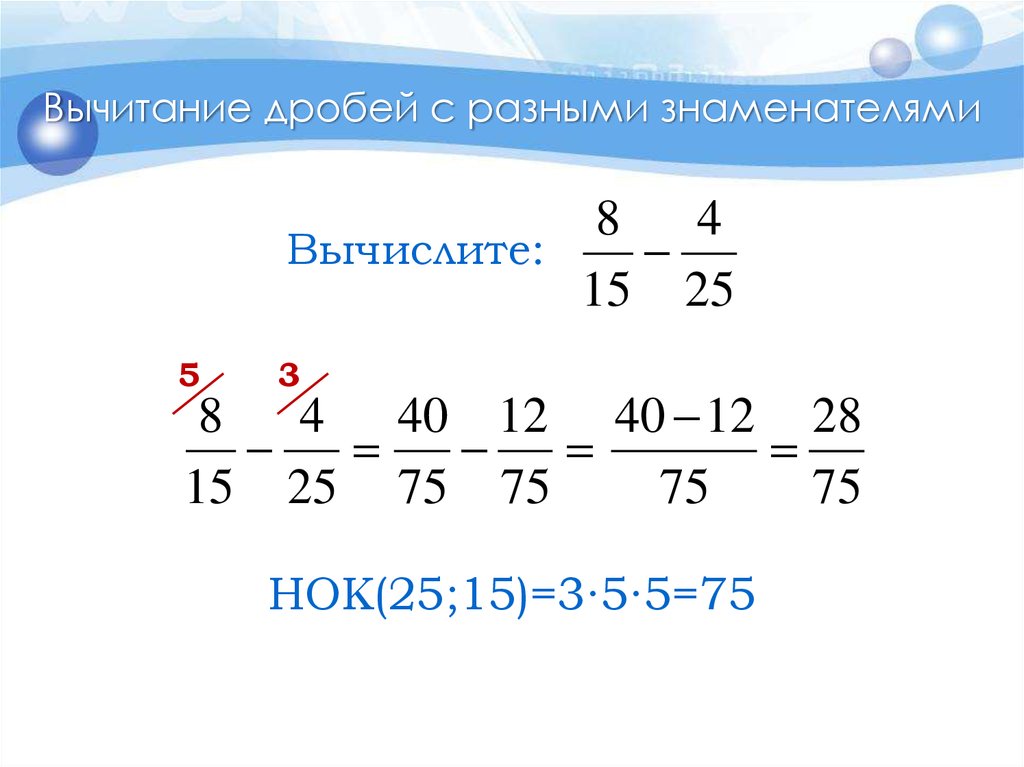
18. Вычитание дробей с разными знаменателями

8
4
Вычислите:
15 25
5
3
8
4 40 12 40 12 28
15 25 75 75
75
75
НОК(25;15)=3∙5∙5=75

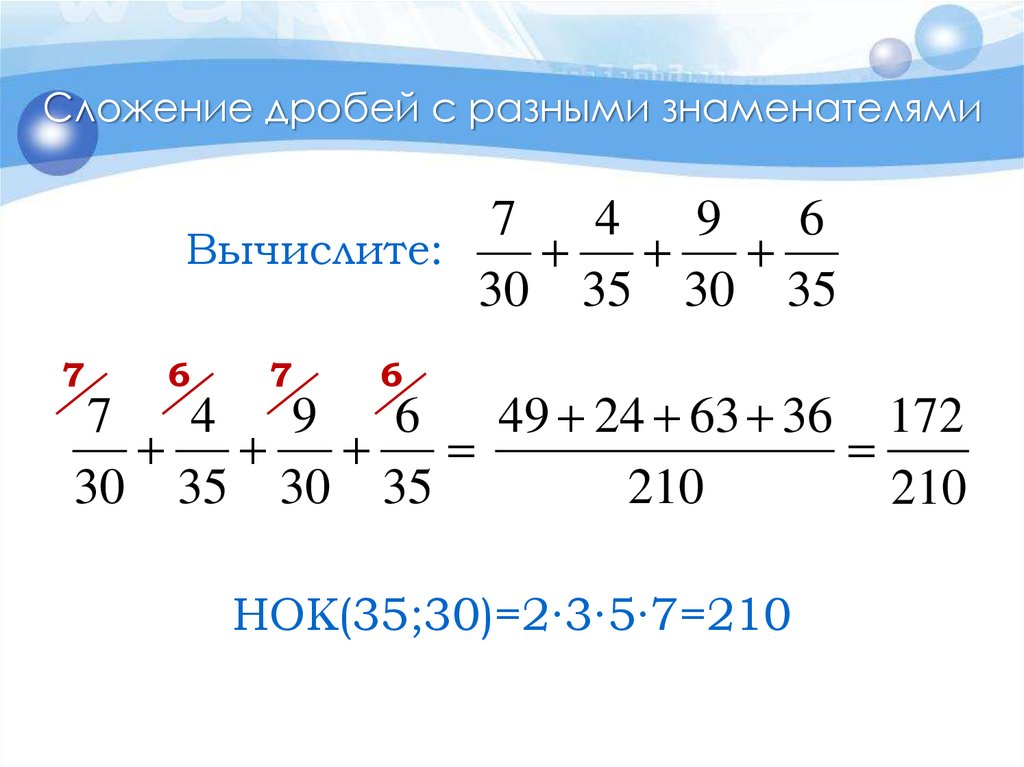
19. Сложение дробей с разными знаменателями

7
4
9
6
Вычислите:
30 35 30 35
7
6
7
6
7
4
9
6
49 24 63 36 172
30 35 30 35
210
210
НОК(35;30)=2∙3∙5∙7=210

20. Сложение и вычитание дробей с разными знаменателями

27 19 1
Вычислите:
60 60 15
1
4
29 19 1 29 19 1 10 1
60 60 15 60 60 15 60 15
10 4 6
1
60 10
60
НОК(60;15)=2∙2∙3∙5=60

21. Сложение и вычитание смешанных чисел

Вычислите:
3
1
2 4
5
10
2
1
3
1
3 1
2 4 2 4
5
10
5 10
6 1
7
7
6
6 6
10
10
10

22. Сложение и вычитание смешанных чисел

7
5
Вычислите: 9
12
12
6
1
2
7
5
7 5
9 12 9 12
12
6
12 6
7 10
17
5
5
21
21
21 1 22
12
12
12
12

23. Сложение и вычитание смешанных чисел

Вычислите:
2
13 8
9
2
9
2
13 8 12 8
9
9
9
9 2
7
7
12 8
4 4
9
9
9

24. Сложение и вычитание смешанных чисел

Вычислите:
3
1
7 4
4
8
2
1
3
1
3 1
7 4 7 4
4
8
4 8
6 1
5
5
3
3 3
8
8
8

25. Сложение и вычитание смешанных чисел

7
5
Вычислите: 29
12
12
6
1
2
7
5
7 10
7 5
29 12 29 12 17
12
6
12
12 6
12 7 10
12 7 10
9
3
16
16
16 16
12
12
12
12
4

26.

Дружественные числа
Древнегреческими учеными –
последователями Пифагора
открыты дружественные
числа – два натуральных
числа для которых сумма
всех делителей первого числа
(кроме него самого) равна
второму числу и сумма всех
делителей второго числа
(кроме него самого) равна
первому числу.
Пифагорейцы знали только
одну пару таких чисел –
220 и 284

27.

Использованы материалы
• Математика. 6 класс: учеб. для общеобразоват. учреждений / Н.Я.
Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. –
М.: Мнемозина, 2013. – 288 с. : ил.
• https://ru.wikipedia.org/wiki/%D4%E8%E3%F3%F0%ED%FB%E5_%F7%E8%F
1%EB%E0 – фигурные числа
• http://mirvolshebstva-anz.blogspot.ru/2012/02/blog-post_01.html – цифры